人教版数学八年级下册课件:18.1.2平行四边形的判定(共25张PPT)
文档属性
| 名称 | 人教版数学八年级下册课件:18.1.2平行四边形的判定(共25张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 299.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-12-24 00:00:00 | ||
图片预览






文档简介
平行四边形的判定
第十八章
平行四边形
人教版八年级数学下册
前面我们学行四边形的定义和性质,它们的内容是什么?
平行四边形的定义:
两组对边分别平行的四边形叫平行四边形;
平行四边形的性质:
对边相等,对角相等,对角线互相平分.
新课导入
一、复习反思,引出课题
学习完定义和性质后,由以前经验接下来我们应该研究什么?
平行四边形的判定
?
判定
性质
定义
新课导入
根据以往学习一些图形判定定理的经验,如何寻找平行四边形的判定方法?
{775DCB02-9BB8-47FD-8907-85C794F793BA}性质定理
判定定理
两直线平行,同位角相等
角平分线上的点到角两边的距离相等
线段垂直平分线上的点到线段两端点的距离相等
全等三角形的对应边相等
……
……
同位角相等,两直线平行
角的内部,到角两边距离相等的点在这个角的角平分线上
到线段两端点距离相等的点在这条线段的垂直平分线上
三条边对应相等的两个三角形全等
新课探究
逆向思考
提出猜想
{35758FB7-9AC5-4552-8A53-C91805E547FA}平行四边形的性质
猜想
对边相等
对角相等
对角线互相平分
两组对边分别相等的四边形是平行四边形
两组对角分别相等的四边形是平行四边形
对角线互相平分的四边形是平行四边形
新课探究
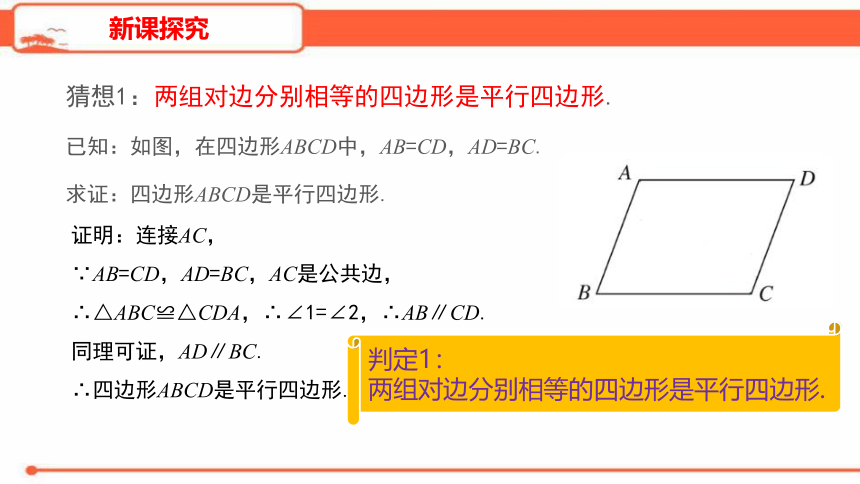
猜想1:两组对边分别相等的四边形是平行四边形.
已知:如图,在四边形ABCD中,AB=CD,AD=BC.
求证:四边形ABCD是平行四边形.
证明:连接AC,
∵AB=CD,AD=BC,AC是公共边,
∴△ABC≌△CDA,∴∠1=∠2,∴AB∥CD.
同理可证,AD∥BC.
∴四边形ABCD是平行四边形.
判定1:
两组对边分别相等的四边形是平行四边形.
新课探究
学生分为两大组,分别对下面两个猜想进行验证.
猜想2:两组对角分别相等的四边形是平行四边形.
猜想3:对角线互相平分的四边形是平行四边形.
新课探究
猜想2:两组对角分别相等的四边形是平行四边形.
已知:如图,在四边形ABCD中,∠A=∠C,∠B=∠D.
求证:四边形ABCD是平行四边形.
证明:∵四边形ABCD是四边形,
∴ ∠A+∠B+∠C+∠D=360°.
又∵ ∠A=∠C,∠B=∠D,
∴ ∠A+∠B=180°,∠B+∠C=180°.
∴ AD∥BC,AB∥DC.
∴ 四边形ABCD是平行四边形.
判定2:
两组对角分别相等的四边形是平行四边形.
新课探究
三、理性思考,证明定理
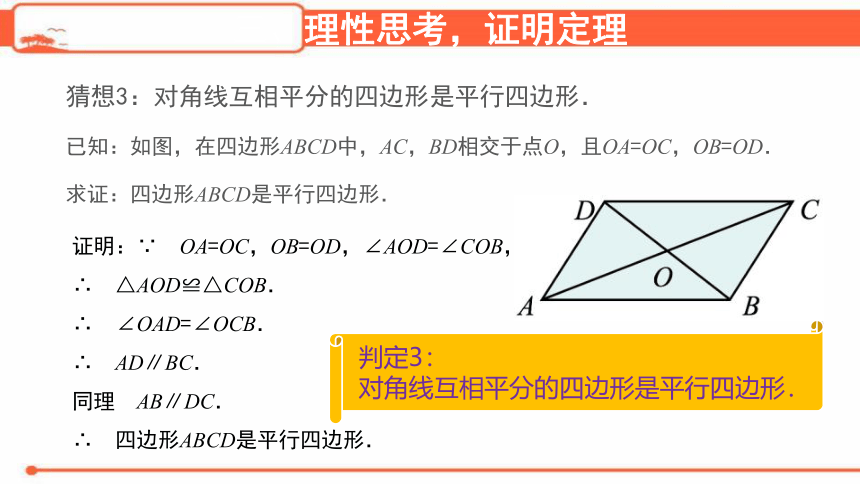
猜想3:对角线互相平分的四边形是平行四边形.
已知:如图,在四边形ABCD中,AC,BD相交于点O,且OA=OC,OB=OD.
求证:四边形ABCD是平行四边形.
证明:∵ OA=OC,OB=OD,∠AOD=∠COB,
∴ △AOD≌△COB.
∴ ∠OAD=∠OCB.
∴ AD∥BC.
同理 AB∥DC.
∴ 四边形ABCD是平行四边形.
判定3:
对角线互相平分的四边形是平行四边形.
两组对边分别平行
两组对边分别相等
两组对角分别相等
对角线互相平分
的四边形是平行四边形
新课探究
例1
如图,AB=DC=EF,AD=BC,DE=CF.求证:AB∥EF.
证明:∵ AB=DC,AD=BC,
∴ 四边形ABCD是平行四边形.
∴ AB∥DC.
又∵ DC=EF,DE=CF,
∴ 四边形DCFE也是平行四边形.
∴ DC∥EF.
∴ AB∥EF.
例题精析
例2
如图,□ABCD中,E,F分别是对角线AC上的两点,并且AE=CF.
求证:四边形BFDE是平行四边形.
证明:连接BD,AC与BD交于O.
∵四边形ABCD是平行四边形,
∴OA=OC,OB=OD,
又∵AE=CF,
∴OA-AE=OC-CF,即OE=OF.
∴OB=OD,OE=OF,
∴四边形BEDF是平行四边形.
O
新课探究
例3
如图所示,已知四边形ABCD是平行四边形,DE
平分∠ADC,交CB的延长线于点E,BF平分
∠ABC,交AD的延长线于点F.
求证:四边形BFDE是平行四
边形.
例题精析
∵四边形ABCD是平行四边形,
∴∠ADC=∠ABC,AD∥CB.
∴DF∥BE.
∵DE平分∠ADC,BF平分∠ABC,
∴∠1=∠2=∠3=∠4.
∵AD∥BC,∴∠1=∠E.
∴∠E=∠3.
∴DE∥FB.
∴四边形BFDE是平行四边形.(两组对边分别
平行的四边形是平行四边形)
证明:
例题精析
例4
如图,分别以△ABC的三边为一边,在BC的同侧
作等边三角形ABD,等边三角形BCE,等边三角
形ACF,连接DE,EF.
求证:四边形ADEF是平行四边形.
例题精析
∵△ABD、△BCE、△ACF都为等边三角形,
∴DB=AB=AD,BE=BC,AC=AF,
∠DBA=60°,∠EBC=60°.
∴∠DBE=60°-∠EBA,∠ABC=60°-∠EBA,
∴∠DBE=∠ABC,∴△DBE≌△ABC,
∴DE=AC.
又∵AC=AF,∴AF=DE.
同理可证:△ABC≌△FEC,
∴AB=FE,∴FE=AD,
∴四边形ADEF是平行四边形.
证明:
例题精析
1.在四边形ABCD中,AB=3
cm,BC=5
cm,那么当DC=__
cm,AD=___
cm时,四边形ABCD是平行四边形.
2.如图,以△ABC的顶点A为圆心,以BC长为半径作弧,
再以顶点C为圆心,以AB长为半径作弧,两弧交于点D,连接AD,CD.
若∠B=65°,则∠ADC的大小为____.
3
5
65°
课堂精练
4.(2019·鸡西)如图,在四边形ABCD中,AD=BC,
在不添加任何辅助线的情况下,请你添加一个条件__________,使四边形ABCD是平行四边形.
3.如图,已知∠B=∠D,要使四边形ABCD
成为平行四边形,需要添加一个条件是______________.
∠A=∠C等
AD∥BC
课堂精练
5.若∠A,∠B,∠C,∠D为四边形ABCD的四个内角,下列给出的是这四个内角的比值,其中能使四边形ABCD是平行四边形的是(
)
A.2∶3∶2∶3
B.2∶3∶3∶2
C.1∶2∶3∶4
D.2∶2∶3∶3
A
课堂精练
6.小玲的爸爸在钉制平行四边形框架时,采用了一种方法:
如图,将两根木条AC,BD的中点重叠,并用钉子固定,
则四边形ABCD就是平行四边形,这种方法的依据是(
)
A.对角线互相平分的四边形是平行四边形
B.两组对角分别相等的四边形是平行四边形
C.两组对边分别相等的四边形是平行四边形
D.两组对边分别平行的四边形是平行四边形
A
课堂精练
7.(呼和浩特中考)顺次连接平面上A,B,C,D四点得到一个四边形,从①AB∥CD;②BC=AD;③∠A=∠C;④∠B=∠D四个条件中任取其中两个,可以得出“四边形ABCD是平行四边形”这一结论的情况共有(
)
A.5种
B.4种
C.3种
D.1种
C
课堂精练
8.(2019·威海)如图,E是?ABCD边AD延长线上一点,
连接BE,CE,BD,BE交CD于点F.添加以下条件,
不能判定四边形BCED为平行四边形的是(
)
A.∠ABD=∠DCE
B.DF=CF
C.∠AEB=∠BCD
D.∠AEC=∠CBD
C
课堂精练
9.
如图,在?ABCD中,点E,F
在对角线BD上,且BE=DF,
求证:四边形AECF是平行四边形.
证明:连接AC,交BD于点O,∵四边形ABCD
是平行四边形,
∴AO=OC,BO=DO,又∵BE=DF,∴BO-BE=DO-DF,
即EO=OF,∴四边形AECF是平行四边形
课堂精练
10.(2019·淮安)已知:如图,在?ABCD中,
点E,F分别是边AD,BC的中点.
求证:BE=DF.
课堂精练
1.平行四边形的判定方法:
①边:两组对边分别平行的四边形是平行四边形;
②边:两组对边分别相等的四边形是平行四边形;
③角:两组对角分别相等的四边形是平行四边形;
④对角线:对角线互相平分的四边形是平行四边形.
2.研究图形的一般思路:
课堂小结
第十八章
平行四边形
人教版八年级数学下册
前面我们学行四边形的定义和性质,它们的内容是什么?
平行四边形的定义:
两组对边分别平行的四边形叫平行四边形;
平行四边形的性质:
对边相等,对角相等,对角线互相平分.
新课导入
一、复习反思,引出课题
学习完定义和性质后,由以前经验接下来我们应该研究什么?
平行四边形的判定
?
判定
性质
定义
新课导入
根据以往学习一些图形判定定理的经验,如何寻找平行四边形的判定方法?
{775DCB02-9BB8-47FD-8907-85C794F793BA}性质定理
判定定理
两直线平行,同位角相等
角平分线上的点到角两边的距离相等
线段垂直平分线上的点到线段两端点的距离相等
全等三角形的对应边相等
……
……
同位角相等,两直线平行
角的内部,到角两边距离相等的点在这个角的角平分线上
到线段两端点距离相等的点在这条线段的垂直平分线上
三条边对应相等的两个三角形全等
新课探究
逆向思考
提出猜想
{35758FB7-9AC5-4552-8A53-C91805E547FA}平行四边形的性质
猜想
对边相等
对角相等
对角线互相平分
两组对边分别相等的四边形是平行四边形
两组对角分别相等的四边形是平行四边形
对角线互相平分的四边形是平行四边形
新课探究
猜想1:两组对边分别相等的四边形是平行四边形.
已知:如图,在四边形ABCD中,AB=CD,AD=BC.
求证:四边形ABCD是平行四边形.
证明:连接AC,
∵AB=CD,AD=BC,AC是公共边,
∴△ABC≌△CDA,∴∠1=∠2,∴AB∥CD.
同理可证,AD∥BC.
∴四边形ABCD是平行四边形.
判定1:
两组对边分别相等的四边形是平行四边形.
新课探究
学生分为两大组,分别对下面两个猜想进行验证.
猜想2:两组对角分别相等的四边形是平行四边形.
猜想3:对角线互相平分的四边形是平行四边形.
新课探究
猜想2:两组对角分别相等的四边形是平行四边形.
已知:如图,在四边形ABCD中,∠A=∠C,∠B=∠D.
求证:四边形ABCD是平行四边形.
证明:∵四边形ABCD是四边形,
∴ ∠A+∠B+∠C+∠D=360°.
又∵ ∠A=∠C,∠B=∠D,
∴ ∠A+∠B=180°,∠B+∠C=180°.
∴ AD∥BC,AB∥DC.
∴ 四边形ABCD是平行四边形.
判定2:
两组对角分别相等的四边形是平行四边形.
新课探究
三、理性思考,证明定理
猜想3:对角线互相平分的四边形是平行四边形.
已知:如图,在四边形ABCD中,AC,BD相交于点O,且OA=OC,OB=OD.
求证:四边形ABCD是平行四边形.
证明:∵ OA=OC,OB=OD,∠AOD=∠COB,
∴ △AOD≌△COB.
∴ ∠OAD=∠OCB.
∴ AD∥BC.
同理 AB∥DC.
∴ 四边形ABCD是平行四边形.
判定3:
对角线互相平分的四边形是平行四边形.
两组对边分别平行
两组对边分别相等
两组对角分别相等
对角线互相平分
的四边形是平行四边形
新课探究
例1
如图,AB=DC=EF,AD=BC,DE=CF.求证:AB∥EF.
证明:∵ AB=DC,AD=BC,
∴ 四边形ABCD是平行四边形.
∴ AB∥DC.
又∵ DC=EF,DE=CF,
∴ 四边形DCFE也是平行四边形.
∴ DC∥EF.
∴ AB∥EF.
例题精析
例2
如图,□ABCD中,E,F分别是对角线AC上的两点,并且AE=CF.
求证:四边形BFDE是平行四边形.
证明:连接BD,AC与BD交于O.
∵四边形ABCD是平行四边形,
∴OA=OC,OB=OD,
又∵AE=CF,
∴OA-AE=OC-CF,即OE=OF.
∴OB=OD,OE=OF,
∴四边形BEDF是平行四边形.
O
新课探究
例3
如图所示,已知四边形ABCD是平行四边形,DE
平分∠ADC,交CB的延长线于点E,BF平分
∠ABC,交AD的延长线于点F.
求证:四边形BFDE是平行四
边形.
例题精析
∵四边形ABCD是平行四边形,
∴∠ADC=∠ABC,AD∥CB.
∴DF∥BE.
∵DE平分∠ADC,BF平分∠ABC,
∴∠1=∠2=∠3=∠4.
∵AD∥BC,∴∠1=∠E.
∴∠E=∠3.
∴DE∥FB.
∴四边形BFDE是平行四边形.(两组对边分别
平行的四边形是平行四边形)
证明:
例题精析
例4
如图,分别以△ABC的三边为一边,在BC的同侧
作等边三角形ABD,等边三角形BCE,等边三角
形ACF,连接DE,EF.
求证:四边形ADEF是平行四边形.
例题精析
∵△ABD、△BCE、△ACF都为等边三角形,
∴DB=AB=AD,BE=BC,AC=AF,
∠DBA=60°,∠EBC=60°.
∴∠DBE=60°-∠EBA,∠ABC=60°-∠EBA,
∴∠DBE=∠ABC,∴△DBE≌△ABC,
∴DE=AC.
又∵AC=AF,∴AF=DE.
同理可证:△ABC≌△FEC,
∴AB=FE,∴FE=AD,
∴四边形ADEF是平行四边形.
证明:
例题精析
1.在四边形ABCD中,AB=3
cm,BC=5
cm,那么当DC=__
cm,AD=___
cm时,四边形ABCD是平行四边形.
2.如图,以△ABC的顶点A为圆心,以BC长为半径作弧,
再以顶点C为圆心,以AB长为半径作弧,两弧交于点D,连接AD,CD.
若∠B=65°,则∠ADC的大小为____.
3
5
65°
课堂精练
4.(2019·鸡西)如图,在四边形ABCD中,AD=BC,
在不添加任何辅助线的情况下,请你添加一个条件__________,使四边形ABCD是平行四边形.
3.如图,已知∠B=∠D,要使四边形ABCD
成为平行四边形,需要添加一个条件是______________.
∠A=∠C等
AD∥BC
课堂精练
5.若∠A,∠B,∠C,∠D为四边形ABCD的四个内角,下列给出的是这四个内角的比值,其中能使四边形ABCD是平行四边形的是(
)
A.2∶3∶2∶3
B.2∶3∶3∶2
C.1∶2∶3∶4
D.2∶2∶3∶3
A
课堂精练
6.小玲的爸爸在钉制平行四边形框架时,采用了一种方法:
如图,将两根木条AC,BD的中点重叠,并用钉子固定,
则四边形ABCD就是平行四边形,这种方法的依据是(
)
A.对角线互相平分的四边形是平行四边形
B.两组对角分别相等的四边形是平行四边形
C.两组对边分别相等的四边形是平行四边形
D.两组对边分别平行的四边形是平行四边形
A
课堂精练
7.(呼和浩特中考)顺次连接平面上A,B,C,D四点得到一个四边形,从①AB∥CD;②BC=AD;③∠A=∠C;④∠B=∠D四个条件中任取其中两个,可以得出“四边形ABCD是平行四边形”这一结论的情况共有(
)
A.5种
B.4种
C.3种
D.1种
C
课堂精练
8.(2019·威海)如图,E是?ABCD边AD延长线上一点,
连接BE,CE,BD,BE交CD于点F.添加以下条件,
不能判定四边形BCED为平行四边形的是(
)
A.∠ABD=∠DCE
B.DF=CF
C.∠AEB=∠BCD
D.∠AEC=∠CBD
C
课堂精练
9.
如图,在?ABCD中,点E,F
在对角线BD上,且BE=DF,
求证:四边形AECF是平行四边形.
证明:连接AC,交BD于点O,∵四边形ABCD
是平行四边形,
∴AO=OC,BO=DO,又∵BE=DF,∴BO-BE=DO-DF,
即EO=OF,∴四边形AECF是平行四边形
课堂精练
10.(2019·淮安)已知:如图,在?ABCD中,
点E,F分别是边AD,BC的中点.
求证:BE=DF.
课堂精练
1.平行四边形的判定方法:
①边:两组对边分别平行的四边形是平行四边形;
②边:两组对边分别相等的四边形是平行四边形;
③角:两组对角分别相等的四边形是平行四边形;
④对角线:对角线互相平分的四边形是平行四边形.
2.研究图形的一般思路:
课堂小结
