人教版数学九 年级下册27.2.3 相似三角形应用举例 ——视线遮挡问题课件(17张)
文档属性
| 名称 | 人教版数学九 年级下册27.2.3 相似三角形应用举例 ——视线遮挡问题课件(17张) |
|
|
| 格式 | ppt | ||
| 文件大小 | 1.5MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-12-24 00:00:00 | ||
图片预览




文档简介
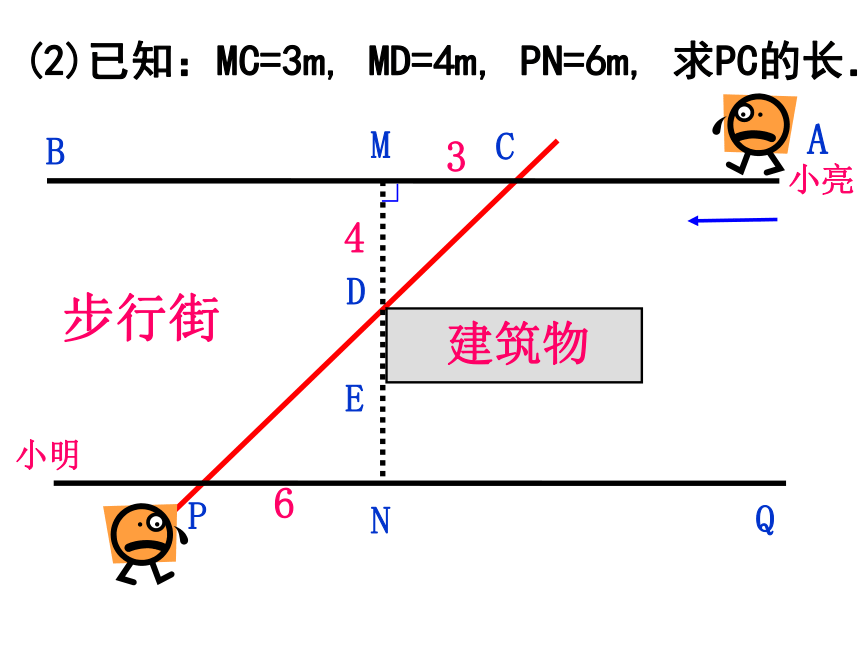
B
M
P
A
Q
D
E
N
建筑物
步行街
∟
(1) 请问小亮走到哪个位置就恰好看见小明
(用点C标出)。
小明
小亮
C
新课引入
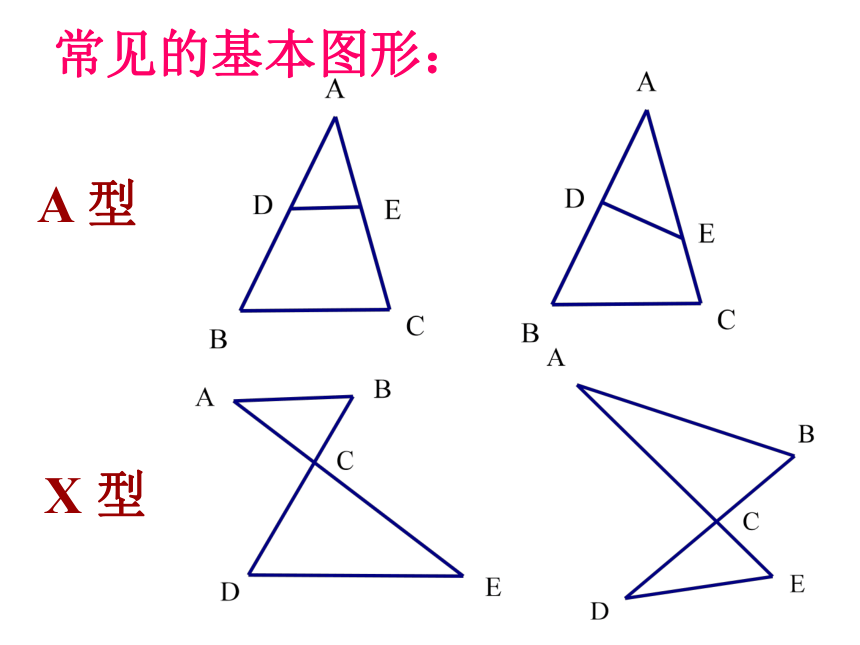
B
M
P
A
Q
D
E
N
建筑物
步行街
∟
小明
小亮
C
3
4
6
(2)已知:MC=3m, MD=4m, PN=6m, 求PC的长.
-----动点问题
定义法;
判定3:两个角对应相等。
通过平行于三角形一边的直线;
判定1:三边对应成比例;
判定2:两边对应成比例且夹角相等;
相似三角形的判定方法有哪些?
知识回顾
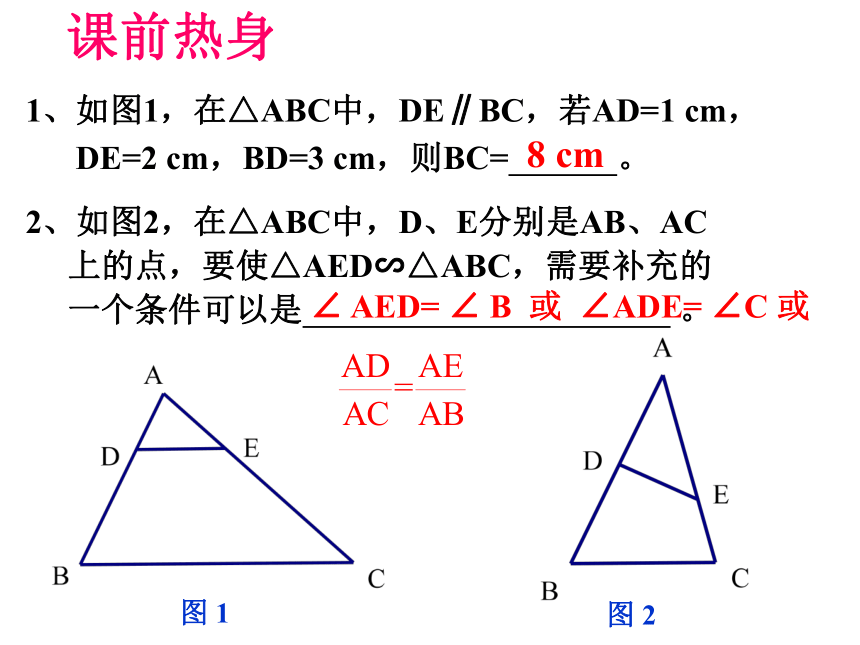
常见的基本图形:
A 型
X 型
1、如图1,在△ABC中,DE∥BC,若AD=1 cm,
DE=2 cm,BD=3 cm,则BC= 。
课前热身
2、如图2,在△ABC中,D、E分别是AB、AC
上的点,要使△AED∽△ABC,需要补充的
一个条件可以是 。
图 1
图 2
8 cm
∠ AED= ∠ B 或 ∠ADE= ∠C 或
3、如图3,已知AC∥BD,OA:OB=3:5,
CD=32,则OC= ,OD= 。
图 3
12
20
如图,在△ABC中,AB=8cm, BC=16cm,点P
从点A开始沿AB向B点以2 cm∕s的速度移动,点
Q从点B开始沿 BC向C点以4cm∕s的速度移动,
如果P、Q分别从A、B同时出发,经过几秒钟
△PBQ与△ABC相似?
探究:
对应边不确定时,
要分类讨论
解:
设经过x秒后△PBQ与△ABC相似 ,
① 若△QBP∽△ABC , 则
② 若△PBQ∽△ABC , 则
综上可知,2秒或 秒后△PBQ与△ABC相似 。
如图,在梯形ABCD中,AD∥BC,∠A=90°,AB=7,
AD=2,BC=3,点P是线段AB上的一个动点(不与A、
B重合),问点P在运动的过程中,以P、A、D为顶点
的三角形能否与以P、B、C为顶点的三角形相似?如果
不能,请说明理由;如果能,这样的P点有几个?并计
算出AP的长。
变式训练
对应顶点不确定
分类讨论
解:设AP=x,则BP=7-x,
① 若△PAD∽△PBC , 则
②若△PAD∽△CBP , 则
综上可知,这样的P点有3个,AP=1 或 6 或
M
P
A
B
Q
D
E
N
建筑物
步行街
∟
小明
小亮
F
G
∟
若MN=20m,MD=8m,PN=240m,AM=200m,小明的
速度是1m∕s,且小亮的速度是小明的两倍,问
多少秒后两人能恰好看见对方?
实际应用:
8
12
如图,在Rt△ABC中,∠A=90°,AB=8,AC=6,若动点D从点B出发,沿线段BA运动到点A为止,运动速度为每秒2个单位长度,过点D作DE∥BC交AC于点E,设动点D运动的时间为x秒,AE的长为y;
(1)求出y关于x的函数关系式,并写出自变量x的取值范围;
中考演练
(2)当x为何值时,△BDE的面积S有最大值?
最大值是多少?
∴ 当x=2时,S有最大值,且最大值为6.
小结
1、分类讨论
2、转化思想
本节课你有哪些收获?
M
P
A
Q
D
E
N
建筑物
步行街
∟
(1) 请问小亮走到哪个位置就恰好看见小明
(用点C标出)。
小明
小亮
C
新课引入
B
M
P
A
Q
D
E
N
建筑物
步行街
∟
小明
小亮
C
3
4
6
(2)已知:MC=3m, MD=4m, PN=6m, 求PC的长.
-----动点问题
定义法;
判定3:两个角对应相等。
通过平行于三角形一边的直线;
判定1:三边对应成比例;
判定2:两边对应成比例且夹角相等;
相似三角形的判定方法有哪些?
知识回顾
常见的基本图形:
A 型
X 型
1、如图1,在△ABC中,DE∥BC,若AD=1 cm,
DE=2 cm,BD=3 cm,则BC= 。
课前热身
2、如图2,在△ABC中,D、E分别是AB、AC
上的点,要使△AED∽△ABC,需要补充的
一个条件可以是 。
图 1
图 2
8 cm
∠ AED= ∠ B 或 ∠ADE= ∠C 或
3、如图3,已知AC∥BD,OA:OB=3:5,
CD=32,则OC= ,OD= 。
图 3
12
20
如图,在△ABC中,AB=8cm, BC=16cm,点P
从点A开始沿AB向B点以2 cm∕s的速度移动,点
Q从点B开始沿 BC向C点以4cm∕s的速度移动,
如果P、Q分别从A、B同时出发,经过几秒钟
△PBQ与△ABC相似?
探究:
对应边不确定时,
要分类讨论
解:
设经过x秒后△PBQ与△ABC相似 ,
① 若△QBP∽△ABC , 则
② 若△PBQ∽△ABC , 则
综上可知,2秒或 秒后△PBQ与△ABC相似 。
如图,在梯形ABCD中,AD∥BC,∠A=90°,AB=7,
AD=2,BC=3,点P是线段AB上的一个动点(不与A、
B重合),问点P在运动的过程中,以P、A、D为顶点
的三角形能否与以P、B、C为顶点的三角形相似?如果
不能,请说明理由;如果能,这样的P点有几个?并计
算出AP的长。
变式训练
对应顶点不确定
分类讨论
解:设AP=x,则BP=7-x,
① 若△PAD∽△PBC , 则
②若△PAD∽△CBP , 则
综上可知,这样的P点有3个,AP=1 或 6 或
M
P
A
B
Q
D
E
N
建筑物
步行街
∟
小明
小亮
F
G
∟
若MN=20m,MD=8m,PN=240m,AM=200m,小明的
速度是1m∕s,且小亮的速度是小明的两倍,问
多少秒后两人能恰好看见对方?
实际应用:
8
12
如图,在Rt△ABC中,∠A=90°,AB=8,AC=6,若动点D从点B出发,沿线段BA运动到点A为止,运动速度为每秒2个单位长度,过点D作DE∥BC交AC于点E,设动点D运动的时间为x秒,AE的长为y;
(1)求出y关于x的函数关系式,并写出自变量x的取值范围;
中考演练
(2)当x为何值时,△BDE的面积S有最大值?
最大值是多少?
∴ 当x=2时,S有最大值,且最大值为6.
小结
1、分类讨论
2、转化思想
本节课你有哪些收获?
