人教版数学九年级下册27.2.1两角判定法(3)课件(20张)
文档属性
| 名称 | 人教版数学九年级下册27.2.1两角判定法(3)课件(20张) |  | |
| 格式 | pptx | ||
| 文件大小 | 471.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-12-24 19:48:05 | ||
图片预览







文档简介
27.2.1 相似三角形的判定(3)
这两个三角形的三个内角的大小有什么关系?
三个内角对应相等的两个三角形一定相似吗?
三个内角对应相等。
观察你与老师的直角三角尺 ,会相似吗?
(30O 与60O)
思考
相
似
画△ ,使三个角分别为60°,45°, 75° 。
①同桌分别量出两个三角形三边的长度;
②同桌这两个三角形相似吗?
即: 如果一个三角形的三个角分别与另一个三角形的三个角对应相等,那么这两个三角形_______.
相似
一定需三个角吗?
如果一个三角形的两角分别与另一个三角形的两角对应相等,那么这两个三角形相似.
相似三角形的识别方法:
思 考
如果两个三角形仅有一对角是对应相等的,那么它们是否一定相似?
观察
C
A
A'
B
B'
C'
∵ ∠A=∠A', ∠B=∠B'
∴ ΔABC ∽ ΔA'B'C'
用数学符号表示:
相似三角形的识别
(两个角分别对应相等的两个三角形相似)
思考
已知:
△ABC∽△A1B1C1.
求证:
你能证明吗?可要仔细哟!
H
L
A
B
C
A1
B1
C1
Rt△ABC 和 Rt△A1B1C1,
如果一个直角三角形的斜边和一条直角边与另一个直角三角形的斜边和一条直角边对应成比例, 那么这两个直角三角形相似.
判定三角形相似的定理之四
H
L
A
B
C
△ABC∽△A1B1C1.
即
如果
那么
√
A1
B1
C1
Rt△ABC 和 Rt△A1B1C1.
例1 如图所示,在两个直角三角形△ABC和△A′B′C′中,∠B=∠B′=90°,∠A=∠A′,判断这两个三角形是否相似.
C'
B'
A'
C
B
A
例题欣赏
解:∵ ∠B=∠B′=90°(已知),
∠A=∠A′(已知),
∴ △ABC∽△A′B′C′(两个角分别对应相等的两个三角形相似.)
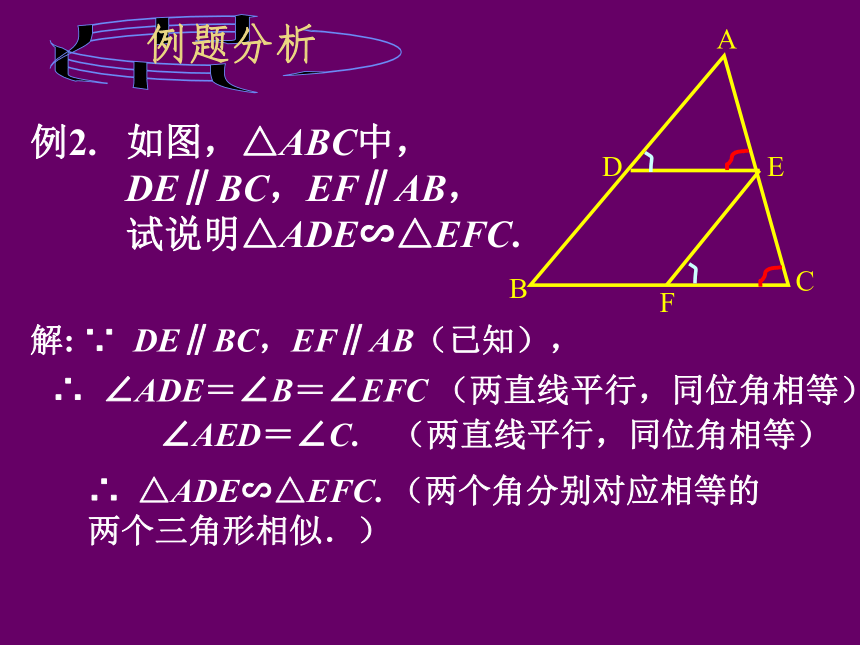
例2. 如图,△ABC中,
DE∥BC,EF∥AB,
试说明△ADE∽△EFC.
A
E
F
B
C
D
用一用
例题分析
解: ∵ DE∥BC,EF∥AB(已知),
∴ ∠ADE=∠B=∠EFC (两直线平行,同位角相等)
∠AED=∠C. (两直线平行,同位角相等)
∴ △ADE∽△EFC. (两个角分别对应相等的两个三角形相似.)
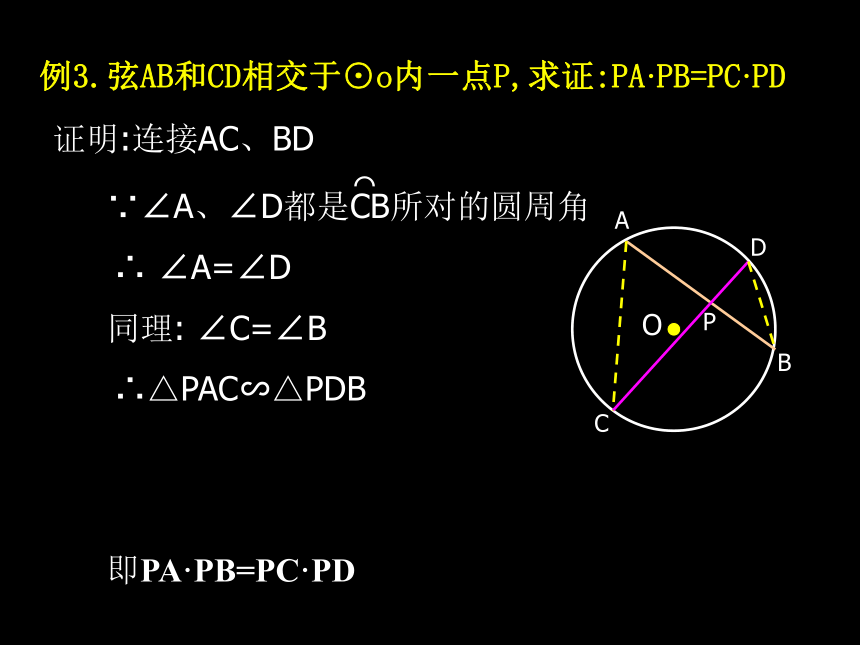
例3.弦AB和CD相交于⊙o内一点P,求证:PA·PB=PC·PD
A
B
C
D
P
O
证明:连接AC、BD
∵∠A、∠D都是CB所对的圆周角
⌒
∴ ∠A=∠D
同理: ∠C=∠B
∴△PAC∽△PDB
即PA·PB=PC·PD
A
B
C
D
E
例4.已知D、E分别是△ABC的边AB,AC上的点,若∠A=35°, ∠C=85°,∠AED=60 °则AD·AB= AE·AC
找一找
F
A
B
C
D
G
E
图 1
(1)图1中DE∥FG∥BC,找出图中所有的相似三角形。
(2)图2中AB∥CD∥EF,找出图中所有的相似三角形。
答:相似三角形有 △ADE∽△AFG∽△ABC。
答:相似三角形有 △AOB∽△FOE∽△DOC。
A
B
图 2
C
F
D
E
O
(3)在△ABC和△A′B′C′中,如果∠A=80°,∠C=60°,∠A′=80°,∠B′=40°,那么这两个三角形是否相似?为什么?
∠B=180 °-(∠A+∠C)=180 °-(80 °+60 °)=40 °
C
A
D
B
3.找出图中所有的相似三角形
巩固练习
△ACD ∽ △ CBD∽ △ ABC
你能写出对应边的比例式吗?
A
B
D
C
图 3
填一填
(1)如图3,点D在AB上,当∠ =∠ 时,
△ACD∽△ABC。
(2)如图4,已知点E在AC上,若点D在AB上,则满足
条件 ,就可以使△ADE与原△ABC相似。
●
A
B
C
E
图 4
ACD
B
(或者∠ ACB=∠ ADB)
DE//BC
D
(或者∠ C=∠ ADE)
(或者∠ B=∠ ADE)
D
解: ∵ ∠ A= ∠ A ∠ABD=∠C
∴ △ABD ∽ △ACB
∴ AB : AC=AD : AB
∴ AB2 = AD · AC
∵ AD=2 AC=8
∴ AB =4
3.已知如图, ∠ABD=∠C AD=2 AC=8,求AB
A
B
C
D
D
B
C
A
18
4 √2
12√2
5、如图:在Rt △ ABC中, ∠ABC=900,BD⊥AC于D
若 AB=6 AD=2 则AC=
BD=
BC=
5、如图:在Rt △ ABC中, ∠ABC=900,BD⊥AC于D
A
B
D
C
E
F
问:若E是BC中点,ED的延长线交BA的延长线于F,
求证:AB : AC=DF : BF
A
B
C
D
E
A
B
C
D
E
2
1
O
C
B
A
D
常见
图形
O
C
D
A
B
A
B
C
D
E
课堂小结
相似图形三角形的判定方法:
通过定义
平行于三角形一边的直线
三边对应成比
两边对应成比例且夹角相等
两角对应相等
两直角三角形的斜边和一条直角边对应成比例
(三边对应成比例,三角相等)
(SSS)
(AA)
(SAS)
(HL)
相似三角形的识别方法有那些?
方法1:通过定义
方法5:通过两角对应相等。
课 堂 小 结
(这可是今天新学的,要牢记噢!)
方法2:平行于三角形一边的直线。
方法3:三边对应成比例。
方法4:两边对应成比例且夹角。
泰勒斯测量金字塔高度的示意图:
A
A′
B C B′ C′
C
B
A
C′
B′
A′
如果人体高度AC=1.7米,人影长BC=2.2米,而B′C′=176米,你能求出金字塔的高度并说明其中的道理吗?
可证△ABC∽△A’B’C’
即
所以A’ C’=1.7x176÷2.2=136m
这两个三角形的三个内角的大小有什么关系?
三个内角对应相等的两个三角形一定相似吗?
三个内角对应相等。
观察你与老师的直角三角尺 ,会相似吗?
(30O 与60O)
思考
相
似
画△ ,使三个角分别为60°,45°, 75° 。
①同桌分别量出两个三角形三边的长度;
②同桌这两个三角形相似吗?
即: 如果一个三角形的三个角分别与另一个三角形的三个角对应相等,那么这两个三角形_______.
相似
一定需三个角吗?
如果一个三角形的两角分别与另一个三角形的两角对应相等,那么这两个三角形相似.
相似三角形的识别方法:
思 考
如果两个三角形仅有一对角是对应相等的,那么它们是否一定相似?
观察
C
A
A'
B
B'
C'
∵ ∠A=∠A', ∠B=∠B'
∴ ΔABC ∽ ΔA'B'C'
用数学符号表示:
相似三角形的识别
(两个角分别对应相等的两个三角形相似)
思考
已知:
△ABC∽△A1B1C1.
求证:
你能证明吗?可要仔细哟!
H
L
A
B
C
A1
B1
C1
Rt△ABC 和 Rt△A1B1C1,
如果一个直角三角形的斜边和一条直角边与另一个直角三角形的斜边和一条直角边对应成比例, 那么这两个直角三角形相似.
判定三角形相似的定理之四
H
L
A
B
C
△ABC∽△A1B1C1.
即
如果
那么
√
A1
B1
C1
Rt△ABC 和 Rt△A1B1C1.
例1 如图所示,在两个直角三角形△ABC和△A′B′C′中,∠B=∠B′=90°,∠A=∠A′,判断这两个三角形是否相似.
C'
B'
A'
C
B
A
例题欣赏
解:∵ ∠B=∠B′=90°(已知),
∠A=∠A′(已知),
∴ △ABC∽△A′B′C′(两个角分别对应相等的两个三角形相似.)
例2. 如图,△ABC中,
DE∥BC,EF∥AB,
试说明△ADE∽△EFC.
A
E
F
B
C
D
用一用
例题分析
解: ∵ DE∥BC,EF∥AB(已知),
∴ ∠ADE=∠B=∠EFC (两直线平行,同位角相等)
∠AED=∠C. (两直线平行,同位角相等)
∴ △ADE∽△EFC. (两个角分别对应相等的两个三角形相似.)
例3.弦AB和CD相交于⊙o内一点P,求证:PA·PB=PC·PD
A
B
C
D
P
O
证明:连接AC、BD
∵∠A、∠D都是CB所对的圆周角
⌒
∴ ∠A=∠D
同理: ∠C=∠B
∴△PAC∽△PDB
即PA·PB=PC·PD
A
B
C
D
E
例4.已知D、E分别是△ABC的边AB,AC上的点,若∠A=35°, ∠C=85°,∠AED=60 °则AD·AB= AE·AC
找一找
F
A
B
C
D
G
E
图 1
(1)图1中DE∥FG∥BC,找出图中所有的相似三角形。
(2)图2中AB∥CD∥EF,找出图中所有的相似三角形。
答:相似三角形有 △ADE∽△AFG∽△ABC。
答:相似三角形有 △AOB∽△FOE∽△DOC。
A
B
图 2
C
F
D
E
O
(3)在△ABC和△A′B′C′中,如果∠A=80°,∠C=60°,∠A′=80°,∠B′=40°,那么这两个三角形是否相似?为什么?
∠B=180 °-(∠A+∠C)=180 °-(80 °+60 °)=40 °
C
A
D
B
3.找出图中所有的相似三角形
巩固练习
△ACD ∽ △ CBD∽ △ ABC
你能写出对应边的比例式吗?
A
B
D
C
图 3
填一填
(1)如图3,点D在AB上,当∠ =∠ 时,
△ACD∽△ABC。
(2)如图4,已知点E在AC上,若点D在AB上,则满足
条件 ,就可以使△ADE与原△ABC相似。
●
A
B
C
E
图 4
ACD
B
(或者∠ ACB=∠ ADB)
DE//BC
D
(或者∠ C=∠ ADE)
(或者∠ B=∠ ADE)
D
解: ∵ ∠ A= ∠ A ∠ABD=∠C
∴ △ABD ∽ △ACB
∴ AB : AC=AD : AB
∴ AB2 = AD · AC
∵ AD=2 AC=8
∴ AB =4
3.已知如图, ∠ABD=∠C AD=2 AC=8,求AB
A
B
C
D
D
B
C
A
18
4 √2
12√2
5、如图:在Rt △ ABC中, ∠ABC=900,BD⊥AC于D
若 AB=6 AD=2 则AC=
BD=
BC=
5、如图:在Rt △ ABC中, ∠ABC=900,BD⊥AC于D
A
B
D
C
E
F
问:若E是BC中点,ED的延长线交BA的延长线于F,
求证:AB : AC=DF : BF
A
B
C
D
E
A
B
C
D
E
2
1
O
C
B
A
D
常见
图形
O
C
D
A
B
A
B
C
D
E
课堂小结
相似图形三角形的判定方法:
通过定义
平行于三角形一边的直线
三边对应成比
两边对应成比例且夹角相等
两角对应相等
两直角三角形的斜边和一条直角边对应成比例
(三边对应成比例,三角相等)
(SSS)
(AA)
(SAS)
(HL)
相似三角形的识别方法有那些?
方法1:通过定义
方法5:通过两角对应相等。
课 堂 小 结
(这可是今天新学的,要牢记噢!)
方法2:平行于三角形一边的直线。
方法3:三边对应成比例。
方法4:两边对应成比例且夹角。
泰勒斯测量金字塔高度的示意图:
A
A′
B C B′ C′
C
B
A
C′
B′
A′
如果人体高度AC=1.7米,人影长BC=2.2米,而B′C′=176米,你能求出金字塔的高度并说明其中的道理吗?
可证△ABC∽△A’B’C’
即
所以A’ C’=1.7x176÷2.2=136m
