人教版数学七年级上册4.3.2 角的比较和运算 课件(20张)
文档属性
| 名称 | 人教版数学七年级上册4.3.2 角的比较和运算 课件(20张) |  | |
| 格式 | ppt | ||
| 文件大小 | 1.5MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-12-24 19:46:05 | ||
图片预览




文档简介
角的比较与运算(1)
七年级数学 第四章 第二节
1.什么是角?
复习回顾
2. 比较线段长短的方法有哪些?
定义一:有公共端点的两条射线组成的图形
定义二:由一条射线绕着它的端点旋转而成的图形
?、叠合法
?、度量法
比较方法有:?、观察法
如何比较两个角的大小,并说说你的比较方法.
B
A
C
E
D
F
你的方法有:
3. 叠合法比较
1. 观察法比较
自主学习,获取新知
2. 度量法比较
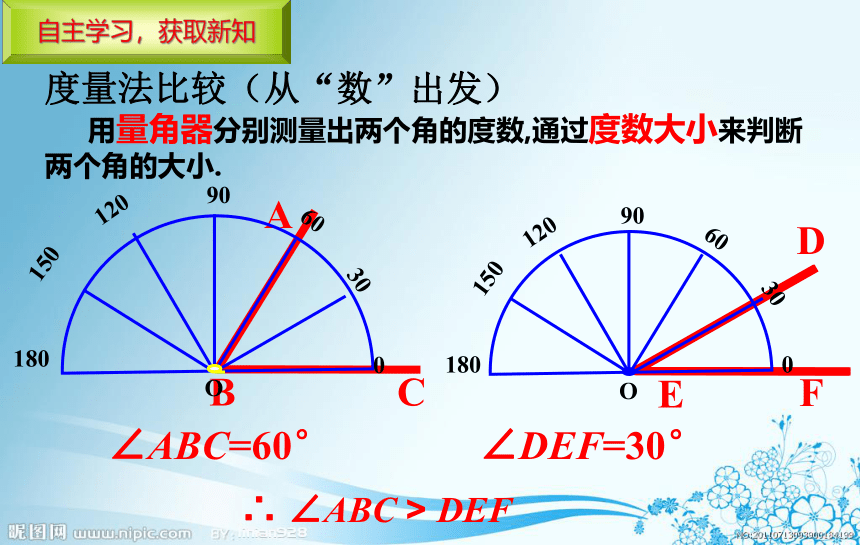
度量法比较(从“数”出发)
C
A
B
O
30
0
60
90
120
150
180
∠ABC=60°
F
D
E
O
30
0
60
90
120
150
180
∠DEF=30°
∴ ∠ABC > DEF
用量角器分别测量出两个角的度数,通过度数大小来判断两个角的大小.
自主学习,获取新知
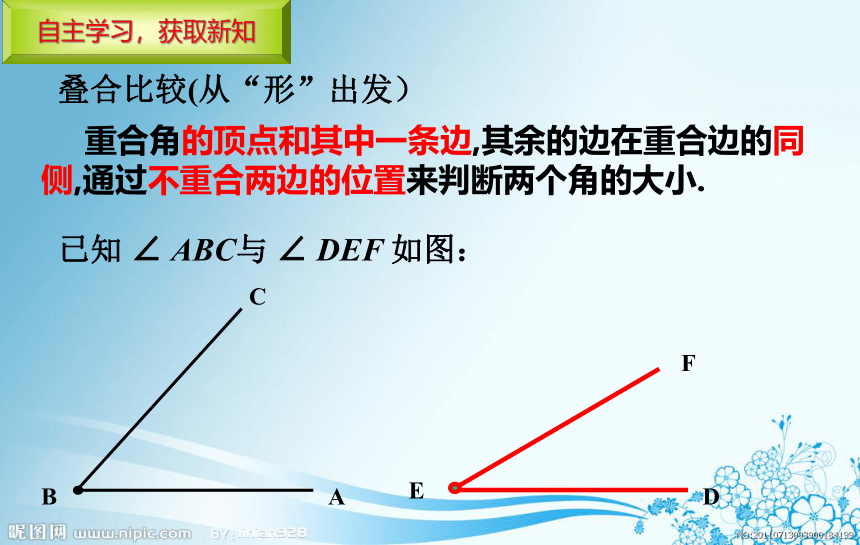
叠合比较(从“形”出发)
已知 ∠ ABC与 ∠ DEF 如图:
A
B
C
重合角的顶点和其中一条边,其余的边在重合边的同侧,通过不重合两边的位置来判断两个角的大小.
自主学习,获取新知
D
E
F
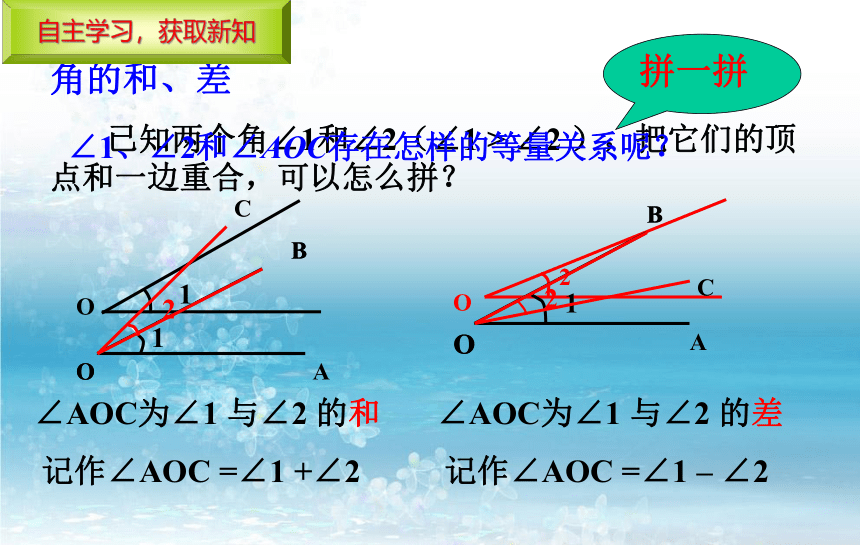
角的和、差
已知两个角∠1和∠2(∠1 > ∠2 ),把它们的顶点和一边重合,可以怎么拼?
2
O
O
1
1
O
A
B
2
C
B
O
A
1
B
O
O
B
C
2
∠AOC为∠1 与∠2 的和
记作∠AOC =∠1 +∠2
∠AOC为∠1 与∠2 的差
记作∠AOC =∠1 – ∠2
拼一拼
自主学习,获取新知
∠1、∠2和∠AOC存在怎样的等量关系呢?
学以致用,内化新知
练习1:填空
(1)如图,若∠AOC=50?,∠AOB=30?,
则 ∠BOC= ;
(2)如图,若∠AOB=50?,
∠BOC=20?,
则 ∠AOC= .
20?
70?
(3)若∠AOC=50?,∠AOB=30?,
则 ∠BOC= ;
20?或80?
学以致用,内化新知
练习1:填空
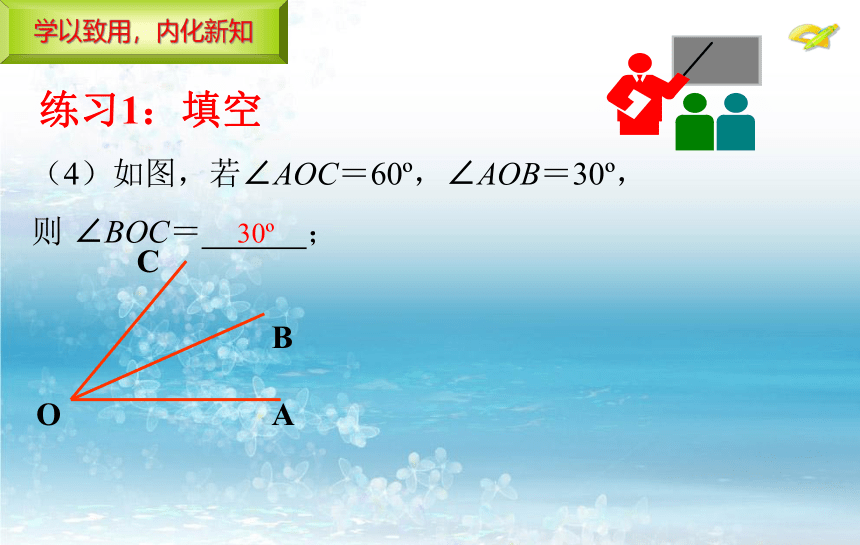
(4)如图,若∠AOC=60?,∠AOB=30?,
则 ∠BOC= ;
30?
B
O
C
A
B
O
C
A
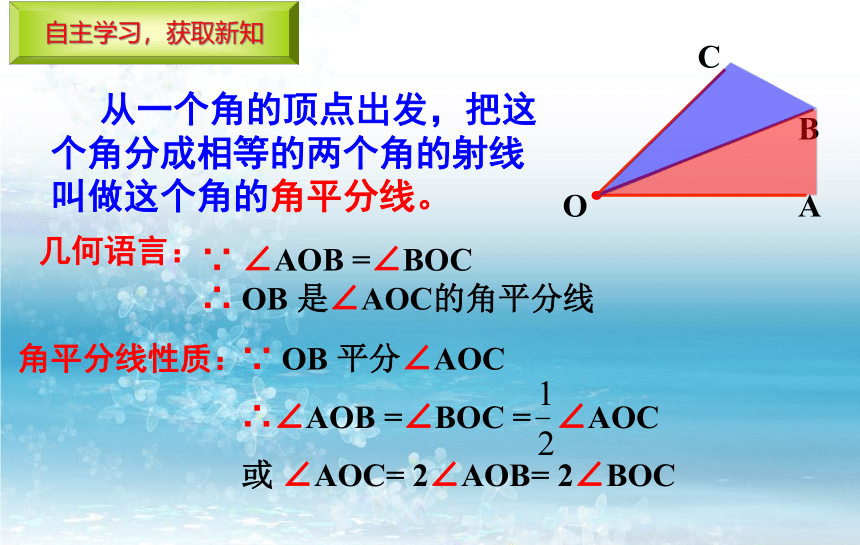
从一个角的顶点出发,把这个角分成相等的两个角的射线叫做这个角的角平分线。
自主学习,获取新知
∵ OB 平分∠AOC
∴∠AOB =∠BOC = ∠AOC
或 ∠AOC= 2∠AOB= 2∠BOC
∵ ∠AOB =∠BOC
∴ OB 是∠AOC的角平分线
几何语言:
角平分线性质:
D
B
C
A
O
如图,射线OB平分∠AOC
(1)若∠AOB=20?,则 ∠BOC= ,∠AOC=________;
(2)若∠AOC=50?,则 ∠BOC= ;
学以致用,内化新知
20?
40?
25?
练习2:
B
C
A
D
O
如图 ∠1=∠2=∠3,
则射线OB 是 的角平分线,
∠AOC
∠2=_____∠AOC,
∠2=_____∠BOD
∠2= ∠AOD
∠AOD
∠BOD = ______
此时,射线OB、OC叫∠AOD的三等分线
学以致用,内化新知
思考:如何作∠AOD的四等分线是?
角的n等分线是?
1
2
3
例1.如图,O是直线AB上一点,∠AOC=54?,求∠BOC的度数.
解:由题意可知,∠AOB是平角,
且∠AOB=∠AOC+∠BOC,
所以∠BOC= ∠AOB-∠AOC
=180?- 54?
=126?.
学以致用,内化新知
E
F
变式1.如图,O是直线AB上一点,∠AOC=54?,OE平分
∠AOC,OF平分 ∠COB,求∠EOF的度数.
所以∠BOC的度数126?.
例2. 已知O为直线AB上一点,过点O向直线上方引三条射线OC、OE、OF,OE平分∠AOC,OF平分 ∠COB,求∠EOF的度数.
解:
∵ OE平分 ∠ AOC,OF平分 ∠COB
∴∠EOF=∠EOC+∠COF
∵∠AOB=∠AOC+∠COB=180°
A
B
E
C
F
O
学以致用,内化新知
∴∠EOC= ∠AOC, ∠COF= ∠COB
= ∠AOC+ ∠COB
= (∠AOC+∠COB)
= 90°
学以致用,内化新知
练习3:填空
1. 如图,已知OD平分∠AOC,OE平分∠BOC,
(2)如图,若∠AOB=110?,
∠AOD=20?, 则 ∠BOE= .
35?
(1)若∠BOC=60?,∠AOC=40?,则 ∠EOD= ;
50?
学以致用,内化新知
练习3:填空
2.如图,已知OD平分∠AOC,OE平分∠AOB,
若∠BOC=90?,则 ∠EOD= ;
45?
1.角的大小比较方法:
2.角的和、差关系.
3.角的平分线.
4.角的运算.
小结反思,回味新知
游戏:
借助三角尺如何画出15°、75°的角?用一副三角尺你还能画出哪些度数的角?
自能拓展,升华新知
30°、45°、60°、90°、 15°、75°、105°、120°、135°、150°、165°、 180°
用角的和、差知识画出所有的特殊角:
自能拓展,升华新知
1.如图,OC平分∠AOD,∠BOD=2∠AOB.若∠AOD=114°,求∠BOC的度数?
A
B
C
D
O
解:∵∠AOD=∠AOB+∠BOD=114°,
∵ OC平分∠AOD
∴∠BOC=∠AOC-∠AOB
∠BOD=2∠AOB
=57°-38°
=19°
自能拓展,升华新知
∴∠AOB= ∠AOD=38°
∴∠AOC= ∠AOD=57°
1. 教科书习题4.3第9,10题.
2.(选做题)已知∠AOB=90°,∠BOC=60°,OD是∠AOC的平分线,求∠BOD的度数.
课后作业
七年级数学 第四章 第二节
1.什么是角?
复习回顾
2. 比较线段长短的方法有哪些?
定义一:有公共端点的两条射线组成的图形
定义二:由一条射线绕着它的端点旋转而成的图形
?、叠合法
?、度量法
比较方法有:?、观察法
如何比较两个角的大小,并说说你的比较方法.
B
A
C
E
D
F
你的方法有:
3. 叠合法比较
1. 观察法比较
自主学习,获取新知
2. 度量法比较
度量法比较(从“数”出发)
C
A
B
O
30
0
60
90
120
150
180
∠ABC=60°
F
D
E
O
30
0
60
90
120
150
180
∠DEF=30°
∴ ∠ABC > DEF
用量角器分别测量出两个角的度数,通过度数大小来判断两个角的大小.
自主学习,获取新知
叠合比较(从“形”出发)
已知 ∠ ABC与 ∠ DEF 如图:
A
B
C
重合角的顶点和其中一条边,其余的边在重合边的同侧,通过不重合两边的位置来判断两个角的大小.
自主学习,获取新知
D
E
F
角的和、差
已知两个角∠1和∠2(∠1 > ∠2 ),把它们的顶点和一边重合,可以怎么拼?
2
O
O
1
1
O
A
B
2
C
B
O
A
1
B
O
O
B
C
2
∠AOC为∠1 与∠2 的和
记作∠AOC =∠1 +∠2
∠AOC为∠1 与∠2 的差
记作∠AOC =∠1 – ∠2
拼一拼
自主学习,获取新知
∠1、∠2和∠AOC存在怎样的等量关系呢?
学以致用,内化新知
练习1:填空
(1)如图,若∠AOC=50?,∠AOB=30?,
则 ∠BOC= ;
(2)如图,若∠AOB=50?,
∠BOC=20?,
则 ∠AOC= .
20?
70?
(3)若∠AOC=50?,∠AOB=30?,
则 ∠BOC= ;
20?或80?
学以致用,内化新知
练习1:填空
(4)如图,若∠AOC=60?,∠AOB=30?,
则 ∠BOC= ;
30?
B
O
C
A
B
O
C
A
从一个角的顶点出发,把这个角分成相等的两个角的射线叫做这个角的角平分线。
自主学习,获取新知
∵ OB 平分∠AOC
∴∠AOB =∠BOC = ∠AOC
或 ∠AOC= 2∠AOB= 2∠BOC
∵ ∠AOB =∠BOC
∴ OB 是∠AOC的角平分线
几何语言:
角平分线性质:
D
B
C
A
O
如图,射线OB平分∠AOC
(1)若∠AOB=20?,则 ∠BOC= ,∠AOC=________;
(2)若∠AOC=50?,则 ∠BOC= ;
学以致用,内化新知
20?
40?
25?
练习2:
B
C
A
D
O
如图 ∠1=∠2=∠3,
则射线OB 是 的角平分线,
∠AOC
∠2=_____∠AOC,
∠2=_____∠BOD
∠2= ∠AOD
∠AOD
∠BOD = ______
此时,射线OB、OC叫∠AOD的三等分线
学以致用,内化新知
思考:如何作∠AOD的四等分线是?
角的n等分线是?
1
2
3
例1.如图,O是直线AB上一点,∠AOC=54?,求∠BOC的度数.
解:由题意可知,∠AOB是平角,
且∠AOB=∠AOC+∠BOC,
所以∠BOC= ∠AOB-∠AOC
=180?- 54?
=126?.
学以致用,内化新知
E
F
变式1.如图,O是直线AB上一点,∠AOC=54?,OE平分
∠AOC,OF平分 ∠COB,求∠EOF的度数.
所以∠BOC的度数126?.
例2. 已知O为直线AB上一点,过点O向直线上方引三条射线OC、OE、OF,OE平分∠AOC,OF平分 ∠COB,求∠EOF的度数.
解:
∵ OE平分 ∠ AOC,OF平分 ∠COB
∴∠EOF=∠EOC+∠COF
∵∠AOB=∠AOC+∠COB=180°
A
B
E
C
F
O
学以致用,内化新知
∴∠EOC= ∠AOC, ∠COF= ∠COB
= ∠AOC+ ∠COB
= (∠AOC+∠COB)
= 90°
学以致用,内化新知
练习3:填空
1. 如图,已知OD平分∠AOC,OE平分∠BOC,
(2)如图,若∠AOB=110?,
∠AOD=20?, 则 ∠BOE= .
35?
(1)若∠BOC=60?,∠AOC=40?,则 ∠EOD= ;
50?
学以致用,内化新知
练习3:填空
2.如图,已知OD平分∠AOC,OE平分∠AOB,
若∠BOC=90?,则 ∠EOD= ;
45?
1.角的大小比较方法:
2.角的和、差关系.
3.角的平分线.
4.角的运算.
小结反思,回味新知
游戏:
借助三角尺如何画出15°、75°的角?用一副三角尺你还能画出哪些度数的角?
自能拓展,升华新知
30°、45°、60°、90°、 15°、75°、105°、120°、135°、150°、165°、 180°
用角的和、差知识画出所有的特殊角:
自能拓展,升华新知
1.如图,OC平分∠AOD,∠BOD=2∠AOB.若∠AOD=114°,求∠BOC的度数?
A
B
C
D
O
解:∵∠AOD=∠AOB+∠BOD=114°,
∵ OC平分∠AOD
∴∠BOC=∠AOC-∠AOB
∠BOD=2∠AOB
=57°-38°
=19°
自能拓展,升华新知
∴∠AOB= ∠AOD=38°
∴∠AOC= ∠AOD=57°
1. 教科书习题4.3第9,10题.
2.(选做题)已知∠AOB=90°,∠BOC=60°,OD是∠AOC的平分线,求∠BOD的度数.
课后作业
