沪科版九年级数学下册24.4_切线长定理 教案
文档属性
| 名称 | 沪科版九年级数学下册24.4_切线长定理 教案 |
|
|
| 格式 | zip | ||
| 文件大小 | 606.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-12-24 19:00:52 | ||
图片预览

文档简介
年级
九年级
教学内容
切线性质定理与切线长定理
教学过程
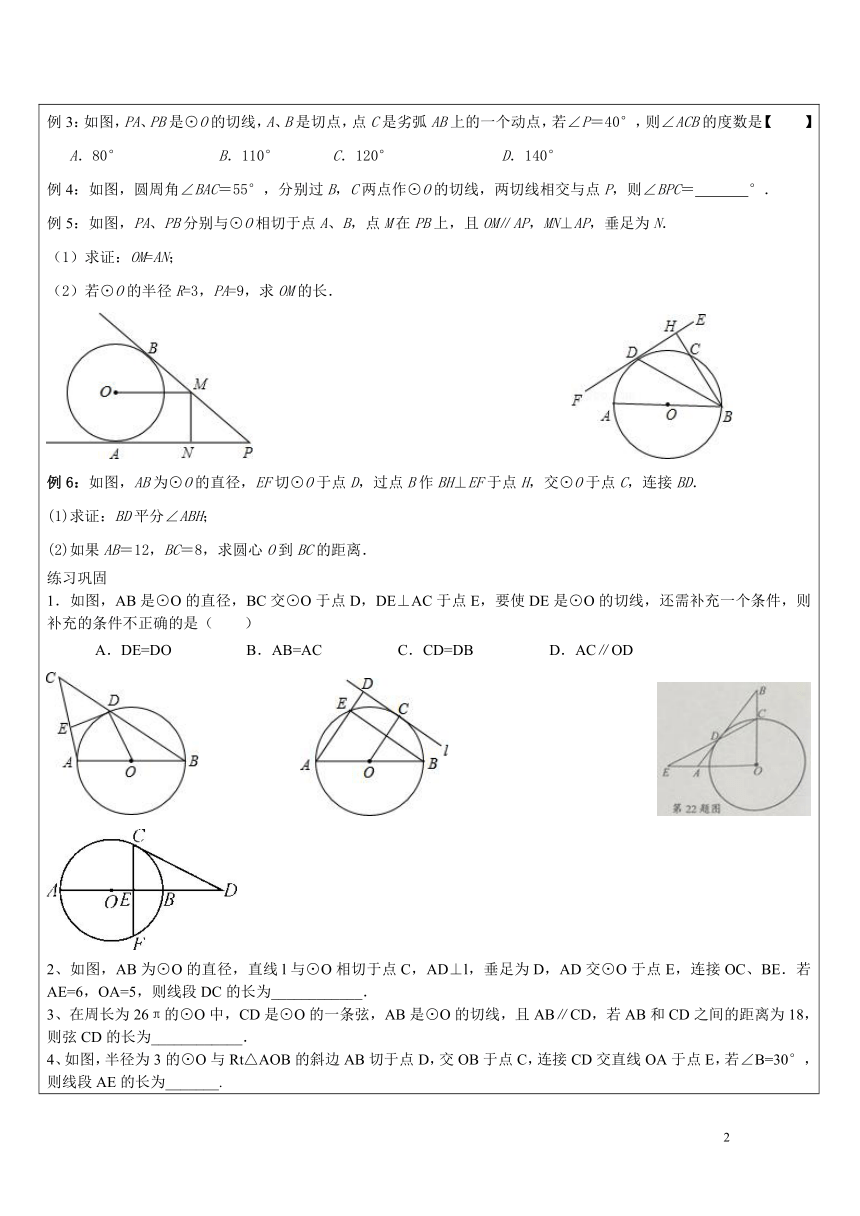
【知识点一、切线性质定理】
性质定理:圆的切线
于经过切点的
∵MN是切线,点A是
∴MN
OA
推论1:过圆心垂直于切线的直线必过切点。
推论2:过切点垂直于切线的直线必过圆心。
知识点一、切线长性质定理】
切线长定理:
从圆外一点引圆的两条切线,它们的切线长
,这点和圆心的连线
两条切线的夹角。
即:∵PA、PB是⊙O的两条切线
∴PA
PB
PO平分
例1:如图,AB是⊙O的直径,C.D是⊙O上一点,∠CDB=20°,过点C作⊙O的切线交AB的延长线于点E,则∠E等于【
】
A.40°
B.50°
C.60°
D.
70°
例2:如图,AB为⊙O的直径,PD切⊙O于点C,交AB的延长线于D,且CO=CD,则∠ACP=【
】
A.
B.
C.
D.
例3:如图,PA、PB是⊙O的切线,A、B是切点,点C是劣弧AB上的一个动点,若∠P=40°,则∠ACB的度数是【 】
A.80°
B.110°
C.120°
D.140°
例4:如图,圆周角∠BAC=55°,分别过B,C两点作⊙O的切线,两切线相交与点P,则∠BPC=
°.
例5:如图,PA、PB分别与⊙O相切于点A、B,点M在PB上,且OM∥AP,MN⊥AP,垂足为N.
(1)求证:OM=AN;
(2)若⊙O的半径R=3,PA=9,求OM的长.
例6:如图,AB为⊙O的直径,EF切⊙O于点D,过点B作BH⊥EF于点H,交⊙O于点C,连接BD.
(1)求证:BD平分∠ABH;
(2)如果AB=12,BC=8,求圆心O到BC的距离.
练习巩固
1.如图,AB是⊙O的直径,BC交⊙O于点D,DE⊥AC于点E,要使DE是⊙O的切线,还需补充一个条件,则补充的条件不正确的是( )
A.DE=DOB.AB=ACC.CD=DBD.AC∥OD
2、如图,AB为⊙O的直径,直线l与⊙O相切于点C,AD⊥l,垂足为D,AD交⊙O于点E,连接OC、BE.若AE=6,OA=5,则线段DC的长为____________.
3、在周长为26π的⊙O中,CD是⊙O的一条弦,AB是⊙O的切线,且AB∥CD,若AB和CD之间的距离为18,则弦CD的长为____________.
4、如图,半径为3的⊙O与Rt△AOB的斜边AB切于点D,交OB于点C,连接CD交直线OA于点E,若∠B=30°,则线段AE的长为_______.
5、如图,AB为⊙O的直径,延长AB至点D,使BD=OB,DC切⊙O于点C,点B是的中点,弦CF交AB于点E,若⊙O的半径为2,则CF=__________.
6、如图,△ABC的边AC与⊙O相交于C,D两点,且经过圆心O,边AB与⊙O相切,切点为B.如果∠A=34°,那么∠C等于( )
A.28°B.33°C.34°D.56°
7、如图,以点O为圆心的两个圆中,大圆的弦AB切小圆于点C,OA交小圆于点D.若OD=2,tan∠OAB=,则AB的长是( ).
A.4
B.2
C.8
D.4
8、如图已知等腰△ABC,AB=BC,以AB为直径的圆交AC于点D,过点D的圆O的切线交BC于点E,若CD=5,CE=4,则圆O的半径是(
)
A.3
B.4
C.
D.
切线长与切线长定理练习
1.如图,PA切⊙O于点A,PB切⊙O于点B,OP交⊙O于点C,则下列结论中错误的是( )
A.∠1=∠2
B.PA=PB
C.AB⊥OP
D.∠PAB=2∠1
2.如图,PA切⊙O于点A,PB切⊙O于点B,连接OP.若∠APO=30°,OA=2,则BP的长为( )
A.
B.
C.4
D.2
3.如图,从⊙O外一点P引⊙O的两条切线PA,PB,切点分别为A,B.若∠APB=60°,弦AB=4,则PA=________.
4.如图,⊙O的半径为3
cm,点P到圆心O的距离为6
cm,过点P引⊙O的两条切线,这两条切线的夹角为________度.
5.教材例5变式
如图24-4-32
,⊙O内切于四边形ABCD,AB=10,CD=8,则AD+BC=________.
6.如图24-4-34,PA,PB是⊙O的切线,切点分别为A,B,OP交AB于点D,交⊙O于点C,AB=4
,DC=2,则∠APB的度数为( )
A.30°
B.45°
C.60°
D.75°
7.如图24-4-35,在矩形ABCD中,AB=4,AD=5,AD,AB,BC分别与⊙O相切于E,F,G三点,过点D作⊙O的切线交BC于点M,切点为N,则DM的长为( )
A.
B.
C.
D.2
8.如图,已知AB为⊙O的直径,PA,PC是⊙O的切线,A,C为切点,∠BAC=30°.
(1)求∠P的度数;
(2)若AB=2,求PA的长(结果保留根号).
【中考变形类型】与切线的性质有关的计算或证明
已知AB是⊙O的直径,AT是⊙O的切线,∠ABT=50°,BT交⊙O于点C,E是AB上一点,延长CE交⊙O于点D.
(1)如图Z12-2①,求∠T和∠CDB的大小;
(2)如图②,当BE=BC时,求∠CDO的大小.
如图Z12-3,AB与⊙O相切于点B,BC为⊙O的弦,OC⊥OA,OA与BC相交于点P.
(1)求证:AP=AB;
(2)若OB=4,AB=3,求线段BP的长.
2
九年级
教学内容
切线性质定理与切线长定理
教学过程
【知识点一、切线性质定理】
性质定理:圆的切线
于经过切点的
∵MN是切线,点A是
∴MN
OA
推论1:过圆心垂直于切线的直线必过切点。
推论2:过切点垂直于切线的直线必过圆心。
知识点一、切线长性质定理】
切线长定理:
从圆外一点引圆的两条切线,它们的切线长
,这点和圆心的连线
两条切线的夹角。
即:∵PA、PB是⊙O的两条切线
∴PA
PB
PO平分
例1:如图,AB是⊙O的直径,C.D是⊙O上一点,∠CDB=20°,过点C作⊙O的切线交AB的延长线于点E,则∠E等于【
】
A.40°
B.50°
C.60°
D.
70°
例2:如图,AB为⊙O的直径,PD切⊙O于点C,交AB的延长线于D,且CO=CD,则∠ACP=【
】
A.
B.
C.
D.
例3:如图,PA、PB是⊙O的切线,A、B是切点,点C是劣弧AB上的一个动点,若∠P=40°,则∠ACB的度数是【 】
A.80°
B.110°
C.120°
D.140°
例4:如图,圆周角∠BAC=55°,分别过B,C两点作⊙O的切线,两切线相交与点P,则∠BPC=
°.
例5:如图,PA、PB分别与⊙O相切于点A、B,点M在PB上,且OM∥AP,MN⊥AP,垂足为N.
(1)求证:OM=AN;
(2)若⊙O的半径R=3,PA=9,求OM的长.
例6:如图,AB为⊙O的直径,EF切⊙O于点D,过点B作BH⊥EF于点H,交⊙O于点C,连接BD.
(1)求证:BD平分∠ABH;
(2)如果AB=12,BC=8,求圆心O到BC的距离.
练习巩固
1.如图,AB是⊙O的直径,BC交⊙O于点D,DE⊥AC于点E,要使DE是⊙O的切线,还需补充一个条件,则补充的条件不正确的是( )
A.DE=DOB.AB=ACC.CD=DBD.AC∥OD
2、如图,AB为⊙O的直径,直线l与⊙O相切于点C,AD⊥l,垂足为D,AD交⊙O于点E,连接OC、BE.若AE=6,OA=5,则线段DC的长为____________.
3、在周长为26π的⊙O中,CD是⊙O的一条弦,AB是⊙O的切线,且AB∥CD,若AB和CD之间的距离为18,则弦CD的长为____________.
4、如图,半径为3的⊙O与Rt△AOB的斜边AB切于点D,交OB于点C,连接CD交直线OA于点E,若∠B=30°,则线段AE的长为_______.
5、如图,AB为⊙O的直径,延长AB至点D,使BD=OB,DC切⊙O于点C,点B是的中点,弦CF交AB于点E,若⊙O的半径为2,则CF=__________.
6、如图,△ABC的边AC与⊙O相交于C,D两点,且经过圆心O,边AB与⊙O相切,切点为B.如果∠A=34°,那么∠C等于( )
A.28°B.33°C.34°D.56°
7、如图,以点O为圆心的两个圆中,大圆的弦AB切小圆于点C,OA交小圆于点D.若OD=2,tan∠OAB=,则AB的长是( ).
A.4
B.2
C.8
D.4
8、如图已知等腰△ABC,AB=BC,以AB为直径的圆交AC于点D,过点D的圆O的切线交BC于点E,若CD=5,CE=4,则圆O的半径是(
)
A.3
B.4
C.
D.
切线长与切线长定理练习
1.如图,PA切⊙O于点A,PB切⊙O于点B,OP交⊙O于点C,则下列结论中错误的是( )
A.∠1=∠2
B.PA=PB
C.AB⊥OP
D.∠PAB=2∠1
2.如图,PA切⊙O于点A,PB切⊙O于点B,连接OP.若∠APO=30°,OA=2,则BP的长为( )
A.
B.
C.4
D.2
3.如图,从⊙O外一点P引⊙O的两条切线PA,PB,切点分别为A,B.若∠APB=60°,弦AB=4,则PA=________.
4.如图,⊙O的半径为3
cm,点P到圆心O的距离为6
cm,过点P引⊙O的两条切线,这两条切线的夹角为________度.
5.教材例5变式
如图24-4-32
,⊙O内切于四边形ABCD,AB=10,CD=8,则AD+BC=________.
6.如图24-4-34,PA,PB是⊙O的切线,切点分别为A,B,OP交AB于点D,交⊙O于点C,AB=4
,DC=2,则∠APB的度数为( )
A.30°
B.45°
C.60°
D.75°
7.如图24-4-35,在矩形ABCD中,AB=4,AD=5,AD,AB,BC分别与⊙O相切于E,F,G三点,过点D作⊙O的切线交BC于点M,切点为N,则DM的长为( )
A.
B.
C.
D.2
8.如图,已知AB为⊙O的直径,PA,PC是⊙O的切线,A,C为切点,∠BAC=30°.
(1)求∠P的度数;
(2)若AB=2,求PA的长(结果保留根号).
【中考变形类型】与切线的性质有关的计算或证明
已知AB是⊙O的直径,AT是⊙O的切线,∠ABT=50°,BT交⊙O于点C,E是AB上一点,延长CE交⊙O于点D.
(1)如图Z12-2①,求∠T和∠CDB的大小;
(2)如图②,当BE=BC时,求∠CDO的大小.
如图Z12-3,AB与⊙O相切于点B,BC为⊙O的弦,OC⊥OA,OA与BC相交于点P.
(1)求证:AP=AB;
(2)若OB=4,AB=3,求线段BP的长.
2
