人教版八年级数学上册考点与题型归纳:12.2全等三角形的判定(Word版 含解析)
文档属性
| 名称 | 人教版八年级数学上册考点与题型归纳:12.2全等三角形的判定(Word版 含解析) |

|
|
| 格式 | zip | ||
| 文件大小 | 575.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-12-24 00:00:00 | ||
图片预览


文档简介
人教版八年级数学上册考点与题型归纳第十二章全等三角形
12.2
全等三角形的判定
一:考点归纳
考点一、三角形全等的判定定理:
(1)边角边定理:有两边和它们的夹角对应相等的两个三角形全等(可简写成“边角边”或“SAS”)
(2)角边角定理:有两角和它们的夹边对应相等的两个三角形全等(可简写成“角边角”或“ASA”)
(3)边边边定理:有三边对应相等的两个三角形全等(可简写成“边边边”或“SSS”)。
考点二、直角三角形全等的判定:
对于特殊的直角三角形,判定它们全等时,还有HL定理(斜边、直角边定理):有斜边和一条直角边对应相等的两个直角三角形全等(可简写成“斜边、直角边”或“HL”)
.考点三、证明的基本方法:
⑴明确命题中的已知和求证.(包括隐含条件,如公共边、公共角、对顶
角、角平分线、中线、高、等腰三角形等所隐含的边角关系)
⑵根据题意,画出图形,并用数字符号表示已知和求证.
⑶经过分析,找出由已知推出求证的途径,写出证明过程.
二:【题型归纳】
题型一:直角三角形全等的判定
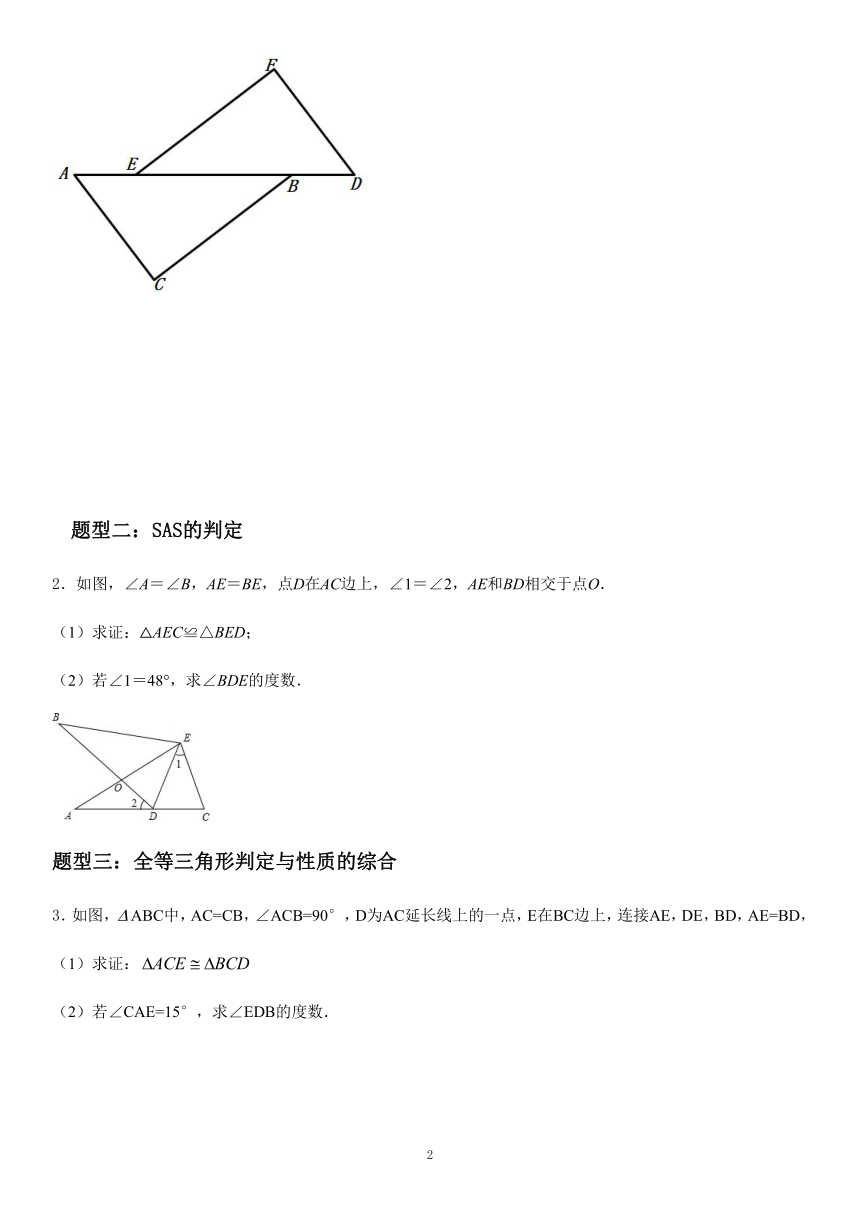
1.如图,已知,垂足分别为点,且.
求证:
题型二:SAS的判定
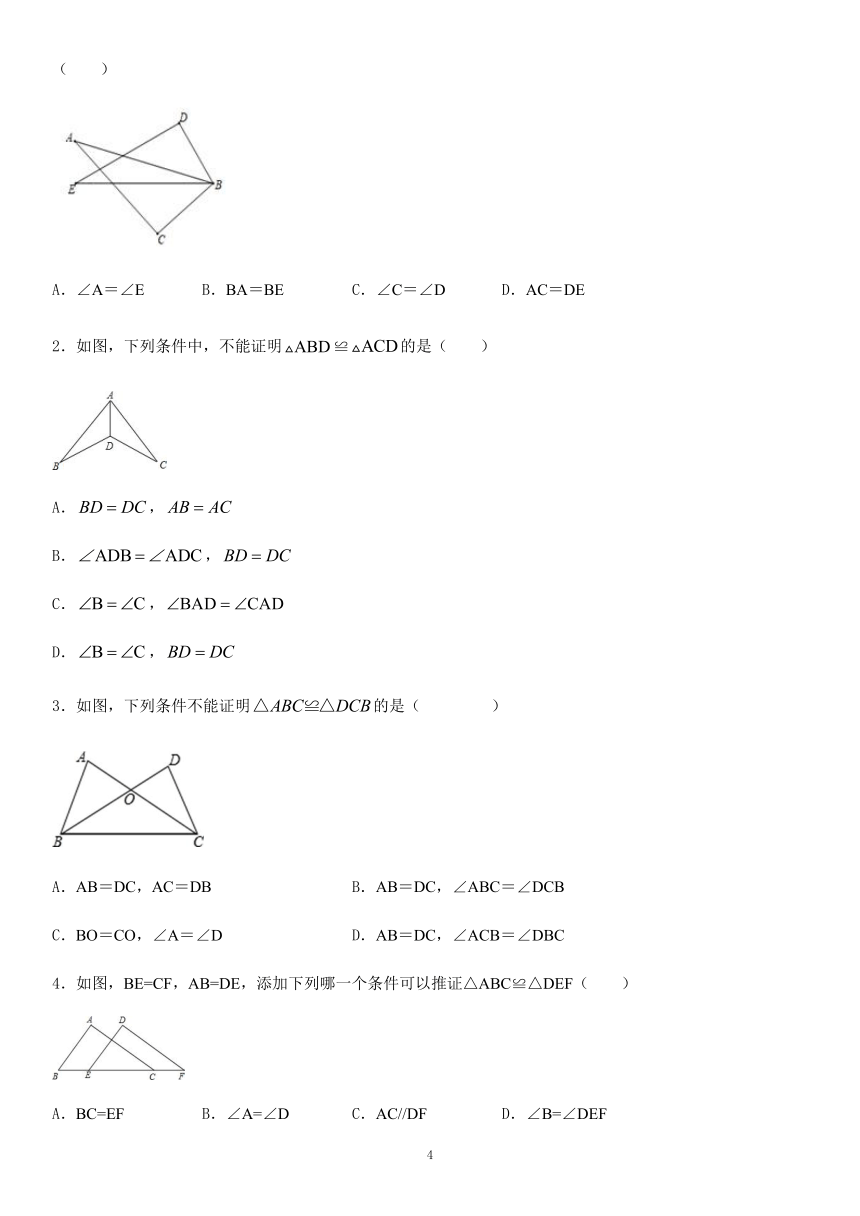
2.如图,∠A=∠B,AE=BE,点D在AC边上,∠1=∠2,AE和BD相交于点O.
(1)求证:△AEC≌△BED;
(2)若∠1=48°,求∠BDE的度数.
题型三:全等三角形判定与性质的综合
3.如图,ABC中,AC=CB,∠ACB=90°,D为AC延长线上的一点,E在BC边上,连接AE,DE,BD,AE=BD,
(1)求证:
(2)若∠CAE=15°,求∠EDB的度数.
4.如图,AD为ABC的高,AD=BD,E为AC上一点,BE交AD于F,且FD=CD.
(1)求证:BFD≌ACD;
(2)判断BE与AC的位置关系,并说明理由.
三:基础巩固和培优
一、单选题
1.如图,∠ABD=∠EBC,BC=BD,再添加一个条件,使得△ABC≌△EBD,所添加的条件不正确的是( )
A.∠A=∠E
B.BA=BE
C.∠C=∠D
D.AC=DE
2.如图,下列条件中,不能证明≌的是(
)
A.,
B.,
C.,
D.,
3.如图,下列条件不能证明的是(
)
A.AB=DC,AC=DB
B.AB=DC,∠ABC=∠DCB
C.BO=CO,∠A=∠D
D.AB=DC,∠ACB=∠DBC
4.如图,BE=CF,AB=DE,添加下列哪一个条件可以推证△ABC≌△DEF( )
A.BC=EF
B.∠A=∠D
C.AC//DF
D.∠B=∠DEF
5.如图,ABC的面积为10,BP平分∠ABC,AP垂直于BP于P.连接CP,若ACP的面积为2,则ABP的面积为(
)
A.1
B.2
C.3
D.4
6.如图,已知AD是ABC的角平分线,增加以下条件:①AB=AC;②∠B=∠C;③AD⊥BC;
④,其中能使BD=CD的条件有
(
)
A.①
B.①②
C.①②③
D.①②③④
7.如图,已知AE=CF,∠AFD=∠CEB,那么添加下列一个条件后,仍无法判定△ADF≌△CBE的是(
)
A.∠B=∠D
B.BE=DF
C.AD=CB
D.AD∥BC
8.如图,在△和△中,已知,还需添加两个条件才能使△≌△,不能添加的一组条件是(
).
A.,
B.,
C.,
D.,
9.如图,,AC=BC.,,垂足分别是点D、E.若AD=6,BE=2,则DE的长是(
)
A.2
B.3
C.4
D.5
10.如图,△ABC的面积为1cm2,
AP垂直∠B的平分线BP于P,则△PBC的面积为(
)
A.0.4
cm2
B.0.5
cm2
C.
cm2
D.0.6
cm2
二、填空题
11.如图所示,在△ABC中,AB=CB,∠ABC=90°,D为AB延长线上一点,点E在BC上,且BE=BD,连接AE、DE、DC.若∠CAE=25°,则∠BDC=_____.
12.在△ABC和△A′B′C′中,若∠A=∠A′,AB=A′B′,请你补充一个条件_____,使得△ABC≌△A′B′C′.
13.如图,在ABC中,点D、E、F分别是BC,AB,AC上的点,若∠B=∠C,BF=CD,BD=CE,∠EDF=56°,则∠A=_____°.
14.如图,已知在中,PR⊥AB于R,PS⊥AC于S,PR=PS,∠1=∠2,则四个结论:①AR=AS;②PQ∥AB;③;④BP=CP中,正确的是________.
15.如图,在△ABC
中,AB=AC=12,BC=8,D
为
AB
的中点,点
P
在线段
BC
上以每秒2
个单位的速度由
B
点向
C
点运动,同时,点
Q
在线段
CA
上以每秒
x
个单位的速度由C
点向
A
点运动.当△BPD
与以
C、Q、P
为顶点的三角形全等时,x
的值为_____.
三、解答题
16.如图所示,在四边形ABCD中,CD∥AB,∠ABC的平分线与∠BCD的平分线相交于点F,BF与CD的延长线交于点E,连接CE.
求证:(1)△BCE是等腰三角形.
(2)BC=AB+CD
17.如图,点B,E,C,F在一条直线上,AB=DE,AC
=DF,BE=CF.求证:△ABC
≌△DEF;
18.如图,D为△ABC外一点,∠DAB=∠B,CD⊥AD,∠1=∠2,若AC=7,BC=4,求AD的长.
19.如图,在△ABC中,AB<AC,边BC的垂直平分线DE交△ABC的外角∠CAM平分线于点D,垂足为E,DF⊥AC于点F,DG⊥AM于点G,连接CD.
(1)求证:BG=CF;
(2)若AB=10cm,AC=14cm,求AG的长.
20.在中,∠ACB=90°,AC=BC,直线,MN经过点C,且AD⊥MN于点D,BE⊥MN于点E.
(1)当直线MN绕点C旋转到如图1的位置时,求证:DE=AD+BE;
(2)当直线MN绕点C旋转到如图2的位置时,求证:DE=AD﹣BE;
(3)当直线MN绕点C旋转到如图3的位置时,线段DE、AD、BE之间又有什么样的数量关系?请你直接写出这个数量关系,不要证明.
试卷第1页,总3页
参考答案
题型归纳
1.证明:
在和中
2.
解:(1)证明:∵AE和BD相交于点O,
∴∠AOD=∠BOE.
在△AOD和△BOE中,
∠A=∠B,∴∠BEO=∠2.
又∵∠1=∠2,
∴∠1=∠BEO,
∴∠AEC=∠BED.
在△AEC和△BED中,
∴△AEC≌△BED(ASA).
(2)∵△AEC≌△BED,
∴EC=ED,∠C=∠BDE.
在△EDC中,
∵EC=ED,∠1=48°,
∴∠C=∠EDC=66°,
∴∠BDE=∠C=66°.
3.
(1)证明:在Rt△ACE和Rt△BCD中,
,
∴△ACE≌△BCD(HL);
(2)∵△ACE≌△BCD,∠CAE=15°,
∴CE=CD,∠CBD=∠CAE=15°
∴∠CDE=∠CED,
∵∠ACB=90°,
∴∠CED=45°,
∵∠CED为△BDE的外角,
∴∠EDB=∠CED-∠CBD=45°-15°=30°.
4.证明:(1)在△BDF和△ADC中,
,
∴△BDF≌△ADC(SAS);
(2)BE⊥AC,
理由如下:
∵△BDF≌△ADC,
∴∠DAC=∠DBF,
∵∠DAC+∠C=90°,
∴∠DBF+∠C=90°,
∴∠BEC=90°,
∴BE⊥AC.
三:基础巩固和培优
1.D
解:∵∠ABD=∠EBC,BC=BD,
∴∠ABC=∠EBD,
A.当添加∠A=∠E时,可根据“AAS”判断△ABC≌△EBD,故正确;
B.当添加BA=BE时,可根据“SAS”判断△ABC≌△EBD,故正确;
C.当添加∠C=∠D时,可根据“ASA”判断△ABC≌△EBD,故正确;
D.当添加AC=DE时,无法判断△ABC≌△EBD,故错误;
故选:D.
2.D
解:A、因为,,又因为AD=AD,所以≌(SSS),故本选项不符合题意;
B、因为,,又因为AD=AD,所以≌(SAS),故本选项不符合题意;
C、因为,,又因为AD=AD,所以≌(AAS),故本选项不符合题意;
D、因为,,AD=AD,这是边边角,不能证明≌,故本选项符合题意.
故选:D.
3.D
解:AB=DC,AC=DB,BC=BC,
符合全等三角形的判定定理“SSS”,
能推出
,故A选项错误;
AB=DC,,BC=CB
符合全等三角形的判定定理“SAS”,
能推出
,故B选项错误;
在△AOB和△DOC中,
,
∴
(AAS),
∴AB=DC,∠ABO=∠DCO,
∵OB=OC,
∴∠OBC=∠OCB,
∴∠ABC=∠DCB,
在△ABC和△DCB中,
,
∴(SAS),
能推出,故C选项错误;
BC=CB,AB=DC,∠ACB=∠DBC,SSA不符合全等三角形的判定定理,即不能推出,故D选项正确.
故选D.
4.D
解:∵BE=CF,∴BC=EF,
又∵AB=DE,
A、添加BC=EF不能证明△ABC≌△DEF,故此选项错误;
B、添加∠A=∠D不能证明△ABC≌△DEF,故此选项错误;
C、添加AC∥DF可得∠ACB=∠F,不能证明△ABC≌△DEF,故此选项错误;
D、添加∠B=∠DEF可利用SAS判定△ABC≌△DEF,故此选项正确;
故选:D.
5.C
解:延长AP交BC于D,
∵BP平分∠ABC,AP⊥BP,
∴∠ABP=∠DBP,∠APB=∠DPB=90°,
在△ABP与△DBP中,
,
∴△ABP≌△DBP(ASA),
∴AP=PD,S△PBD=S△ABP
∴
∴S△ABD=10-4=6,
∴△ABP的面积=3cm2,
故选:C.
6.D
解:∵AD平分∠BAC,
∴∠BAD=∠CAD,
∵AB=AC,AD=AD,
∴△BAD≌△CAD(SAS),
∴BD=CD,故①符合题意;
∵∠B=∠C,AD=AD,
∴△BAD≌△CAD(AAS),
∴BD=CD,故②符合题意;
∵AD⊥BC,
∴∠ADB=∠ADC=90°,
∵AD=AD,
∴△BAD≌△CAD(ASA),
∴BD=DC,故③符合题意;
∵,
∴BD=DC,故④符合题意;
∴①②③④都可以得到BD=CD;
故选D.
7.C
解:∵AE=CF,
∴AE+EF=CF+EF,
∴AF=CE,
A、∠B=∠D,∠AFD=∠CEB,AF=CE,满足AAS,能判定△ADF≌△CBE;
B、BE=DF,∠AFD=∠CEB,AF=CE,满足SAS,能判定△ADF≌△CBE;
C、AD=CB,AF=CE,∠AFD=∠CEB,满足SSA,不能判定△ADF≌△CBE;
D、AD∥BC,则∠A=∠C,又AF=CE,∠AFD=∠CEB,满足ASA,能判定△ADF≌△CBE;
故选:C.
8.C
解:∵CB=CE.
∴当,时,满足SAS,可证△≌△,故A不符合题意;
当,时,满足SSS,可证△≌△,故B不符合题意;
当,时,满足是ASS,不能证明△≌△,故C符合题意;
当,时,满足AAS,可证△≌△,故D不符合题意.
故选C.
9.C
解:∵,
∴∠ACD+∠ECB=90?,
∵,,
∴∠ADC=∠CEB=90?,
∴∠ECB+∠CBE=90?,
∴∠ACD=∠CBE,
在△ACD和△CBE中,
∵∠ADC=∠CEB=90?,∠ACD=∠CBE,AC=BC,
∴△ACD≌△CBE(AAS),
∴AD=CE=6,CD=BE=2,
∴ED=EC-CD=6-2=4.
故选择:C.
10.B
解:如图,延长AP交BC于T.
∵BP⊥AT,
∴∠BPA=∠BPT=90°,
∵BP=BP,∠PBA=∠PBT,
∴△BPA≌△BPT(ASA),
∴PA=PT,
∴S△BPA=S△BPT,S△CAP=S△CPT,
∴S△PBC=S△ABC==0.5,
故选:B.
11.70°
解:
∵∠ABC=90°,
∴∠CBD=∠ABC
=90°,
在Rt△ABE与Rt△CBD中,
∴△ABE≌△CBD,
∴∠AEB=∠BDC,
∵AB=BC,
∴∠BAC=∠ACB=45°,
∵∠AEB为△AEC的外角,∠CAE=25°,
∴∠AEB=∠ACB+∠CAE=45°+25°=70°,
∴∠BDC=70°.
故答案为:70°.
12.∠B=∠B′或∠C=∠C′或AC=A′C′.
解:在△ABC和△A′B′C′中,AB=A′B′,∠A=∠A′,
当添加∠B=∠B′可利用“ASA”判断△ABC≌△A′B′C′;
当添加∠C=∠C′可利用“AAS”判断△ABC≌△A′B′C′;
当添加AC=∠A′C′可利用“SAS”判断△ABC≌△A′B′C′.
故答案为:∠B=∠B′或∠C=∠C′或AC=A′C′.
13.68°.
解:在△BDF和△CED中
∵BF=CD,∠B=∠C,BD=CE,
∴△BDF≌△CED(SAS),
∴∠BFD=∠CDE,∠BDF=∠CED,
∴∠BDF+∠CDE=180?-∠EDF=180?-56?=124?,
∴∠BFD+∠BDF=∠BDF+∠CDE=124?,
∴∠C=∠B=180?-∠BFD-∠BDF=56?,
∴∠A=180?-∠B-∠C=180?-56?-56?=68?.
故答案为:68?.
14.①②
解:在和中,
,
,
,①正确,
∴,
,
,
,②正确,
和中,只有一个条件,再没有其余条件可以证明
,故③④错误;
故答案是:①②.
15.2
或
3
解:设经过
t
秒后,使△BPD
与△CQP
全等.
∵AB=AC=12,点
D
为
AB
的中点.
∴BD=6.
∵∠ABC=∠ACB.
∴要使△BPD
与△CQP
全等,必须
BD=CP
或
BP=CP.
即
6=8﹣2t
或
2t=8﹣2t.
=1,=2.
当t=1
时,BP=CQ=2,2÷1=2.
当t=2
时,BD=CQ=6,6÷2=3.
即点
Q
的运动速度是
2
或
3,
故答案为:2
或
3.
16.解:(1)∵BF平分∠ABC,
∴,
∵CD∥AB,
∴,
∴,
∴BC=CE,
∴△BCE
是等腰三角形.
(2)∵CF平分∠BCE,
∴,
∵CD∥AB,
∴,
∴,
∴,即
CF⊥BE,
又BC=CE,
∴BF=EF,
在△ABF和△DEF中,
∵,
∴△ABF≌△DEF;
∴AB=DE,
∴BC=CE=DE+CD=AB+CD,
因此
BC=AB+CD.
17.
解:证明:∵BE=CF,
∴BE+EC=CF+EC,
∴BC=EF,
在△ABC和△DEF中,
∵,
∴△ABC
≌△DEF(SSS).
18.
解:证明:延长AD,BC交于点E.
∵CD⊥AD,
∴∠ADC=∠EDC=90°.
在△ADC和△EDC中
,
∴△ADC≌△EDC(ASA).
∴∠DAC=∠DEC,AC=EC,AD=ED.
∵AC=7,
∴EC=7.
∵BC=4
∴BE=11
∵∠DAB=∠B,
∴AE=BE=11.
∴AD=5.5.
答:AD的长为5.5.
19.
解:(1)证明:如图所示,连接DB.
∵AD是△ABC的外角平分线,DG⊥AB,DF⊥CA,
∴DF=DG.
∵DE垂直平分BC,
∴DC=DB,
在Rt△CDF与Rt△BDG中
∴Rt△CDF≌Rt△BDG(HL),
∴BG=CF.
(2)解:∵∠GAD=∠FAD,∠AGD=∠AFD,AD=AD,
∴在△ADG与△ADF中
∴△ADG≌△ADF(AAS),
∴AG=AF,
∵BG=CF
∴AG=(cm).
20.解:(1)证明:∵AD⊥MN,BE⊥MN,
∴∠ADC=∠CEB=90°,
∴∠DAC+∠ACD=90°,
∵∠ACB=90°,
∴∠BCE+∠ACD=90°,
∴∠DAC=∠BCE,
在△ADC和△CEB,
,
∴△ADC≌△CEB(AAS),
∴CD=BE,AD=CE,
∴DE=CE+CD=AD+BE;
(2)证明:∵AD⊥MN,BE⊥MN,
∴∠ADC=∠CEB=90°,
∴∠DAC+∠ACD=90°,
∵∠ACB=90°,
∴∠BCE+∠ACD=90°,
∴∠DAC=∠BCE,
∵AC=BC,
∴△ADC≌△CEB,
∴CD=BE,AD=CE,
∴DE=CE﹣CD=AD﹣BE;
(3)解:DE=BE﹣AD,理由如下:
∵AD⊥MN,BE⊥MN,
∴∠ADC=∠CEB=90°,
∴∠DAC+∠ACD=90°,
∵∠ACB=90°,
∴∠BCE+∠ACD=90°,
∴∠DAC=∠BCE,
∵AC=BC,
∴△ADC≌△CEB,
∴CD=BE,AD=CE,
∴DE=BE﹣AD.
12.2
全等三角形的判定
一:考点归纳
考点一、三角形全等的判定定理:
(1)边角边定理:有两边和它们的夹角对应相等的两个三角形全等(可简写成“边角边”或“SAS”)
(2)角边角定理:有两角和它们的夹边对应相等的两个三角形全等(可简写成“角边角”或“ASA”)
(3)边边边定理:有三边对应相等的两个三角形全等(可简写成“边边边”或“SSS”)。
考点二、直角三角形全等的判定:
对于特殊的直角三角形,判定它们全等时,还有HL定理(斜边、直角边定理):有斜边和一条直角边对应相等的两个直角三角形全等(可简写成“斜边、直角边”或“HL”)
.考点三、证明的基本方法:
⑴明确命题中的已知和求证.(包括隐含条件,如公共边、公共角、对顶
角、角平分线、中线、高、等腰三角形等所隐含的边角关系)
⑵根据题意,画出图形,并用数字符号表示已知和求证.
⑶经过分析,找出由已知推出求证的途径,写出证明过程.
二:【题型归纳】
题型一:直角三角形全等的判定
1.如图,已知,垂足分别为点,且.
求证:
题型二:SAS的判定
2.如图,∠A=∠B,AE=BE,点D在AC边上,∠1=∠2,AE和BD相交于点O.
(1)求证:△AEC≌△BED;
(2)若∠1=48°,求∠BDE的度数.
题型三:全等三角形判定与性质的综合
3.如图,ABC中,AC=CB,∠ACB=90°,D为AC延长线上的一点,E在BC边上,连接AE,DE,BD,AE=BD,
(1)求证:
(2)若∠CAE=15°,求∠EDB的度数.
4.如图,AD为ABC的高,AD=BD,E为AC上一点,BE交AD于F,且FD=CD.
(1)求证:BFD≌ACD;
(2)判断BE与AC的位置关系,并说明理由.
三:基础巩固和培优
一、单选题
1.如图,∠ABD=∠EBC,BC=BD,再添加一个条件,使得△ABC≌△EBD,所添加的条件不正确的是( )
A.∠A=∠E
B.BA=BE
C.∠C=∠D
D.AC=DE
2.如图,下列条件中,不能证明≌的是(
)
A.,
B.,
C.,
D.,
3.如图,下列条件不能证明的是(
)
A.AB=DC,AC=DB
B.AB=DC,∠ABC=∠DCB
C.BO=CO,∠A=∠D
D.AB=DC,∠ACB=∠DBC
4.如图,BE=CF,AB=DE,添加下列哪一个条件可以推证△ABC≌△DEF( )
A.BC=EF
B.∠A=∠D
C.AC//DF
D.∠B=∠DEF
5.如图,ABC的面积为10,BP平分∠ABC,AP垂直于BP于P.连接CP,若ACP的面积为2,则ABP的面积为(
)
A.1
B.2
C.3
D.4
6.如图,已知AD是ABC的角平分线,增加以下条件:①AB=AC;②∠B=∠C;③AD⊥BC;
④,其中能使BD=CD的条件有
(
)
A.①
B.①②
C.①②③
D.①②③④
7.如图,已知AE=CF,∠AFD=∠CEB,那么添加下列一个条件后,仍无法判定△ADF≌△CBE的是(
)
A.∠B=∠D
B.BE=DF
C.AD=CB
D.AD∥BC
8.如图,在△和△中,已知,还需添加两个条件才能使△≌△,不能添加的一组条件是(
).
A.,
B.,
C.,
D.,
9.如图,,AC=BC.,,垂足分别是点D、E.若AD=6,BE=2,则DE的长是(
)
A.2
B.3
C.4
D.5
10.如图,△ABC的面积为1cm2,
AP垂直∠B的平分线BP于P,则△PBC的面积为(
)
A.0.4
cm2
B.0.5
cm2
C.
cm2
D.0.6
cm2
二、填空题
11.如图所示,在△ABC中,AB=CB,∠ABC=90°,D为AB延长线上一点,点E在BC上,且BE=BD,连接AE、DE、DC.若∠CAE=25°,则∠BDC=_____.
12.在△ABC和△A′B′C′中,若∠A=∠A′,AB=A′B′,请你补充一个条件_____,使得△ABC≌△A′B′C′.
13.如图,在ABC中,点D、E、F分别是BC,AB,AC上的点,若∠B=∠C,BF=CD,BD=CE,∠EDF=56°,则∠A=_____°.
14.如图,已知在中,PR⊥AB于R,PS⊥AC于S,PR=PS,∠1=∠2,则四个结论:①AR=AS;②PQ∥AB;③;④BP=CP中,正确的是________.
15.如图,在△ABC
中,AB=AC=12,BC=8,D
为
AB
的中点,点
P
在线段
BC
上以每秒2
个单位的速度由
B
点向
C
点运动,同时,点
Q
在线段
CA
上以每秒
x
个单位的速度由C
点向
A
点运动.当△BPD
与以
C、Q、P
为顶点的三角形全等时,x
的值为_____.
三、解答题
16.如图所示,在四边形ABCD中,CD∥AB,∠ABC的平分线与∠BCD的平分线相交于点F,BF与CD的延长线交于点E,连接CE.
求证:(1)△BCE是等腰三角形.
(2)BC=AB+CD
17.如图,点B,E,C,F在一条直线上,AB=DE,AC
=DF,BE=CF.求证:△ABC
≌△DEF;
18.如图,D为△ABC外一点,∠DAB=∠B,CD⊥AD,∠1=∠2,若AC=7,BC=4,求AD的长.
19.如图,在△ABC中,AB<AC,边BC的垂直平分线DE交△ABC的外角∠CAM平分线于点D,垂足为E,DF⊥AC于点F,DG⊥AM于点G,连接CD.
(1)求证:BG=CF;
(2)若AB=10cm,AC=14cm,求AG的长.
20.在中,∠ACB=90°,AC=BC,直线,MN经过点C,且AD⊥MN于点D,BE⊥MN于点E.
(1)当直线MN绕点C旋转到如图1的位置时,求证:DE=AD+BE;
(2)当直线MN绕点C旋转到如图2的位置时,求证:DE=AD﹣BE;
(3)当直线MN绕点C旋转到如图3的位置时,线段DE、AD、BE之间又有什么样的数量关系?请你直接写出这个数量关系,不要证明.
试卷第1页,总3页
参考答案
题型归纳
1.证明:
在和中
2.
解:(1)证明:∵AE和BD相交于点O,
∴∠AOD=∠BOE.
在△AOD和△BOE中,
∠A=∠B,∴∠BEO=∠2.
又∵∠1=∠2,
∴∠1=∠BEO,
∴∠AEC=∠BED.
在△AEC和△BED中,
∴△AEC≌△BED(ASA).
(2)∵△AEC≌△BED,
∴EC=ED,∠C=∠BDE.
在△EDC中,
∵EC=ED,∠1=48°,
∴∠C=∠EDC=66°,
∴∠BDE=∠C=66°.
3.
(1)证明:在Rt△ACE和Rt△BCD中,
,
∴△ACE≌△BCD(HL);
(2)∵△ACE≌△BCD,∠CAE=15°,
∴CE=CD,∠CBD=∠CAE=15°
∴∠CDE=∠CED,
∵∠ACB=90°,
∴∠CED=45°,
∵∠CED为△BDE的外角,
∴∠EDB=∠CED-∠CBD=45°-15°=30°.
4.证明:(1)在△BDF和△ADC中,
,
∴△BDF≌△ADC(SAS);
(2)BE⊥AC,
理由如下:
∵△BDF≌△ADC,
∴∠DAC=∠DBF,
∵∠DAC+∠C=90°,
∴∠DBF+∠C=90°,
∴∠BEC=90°,
∴BE⊥AC.
三:基础巩固和培优
1.D
解:∵∠ABD=∠EBC,BC=BD,
∴∠ABC=∠EBD,
A.当添加∠A=∠E时,可根据“AAS”判断△ABC≌△EBD,故正确;
B.当添加BA=BE时,可根据“SAS”判断△ABC≌△EBD,故正确;
C.当添加∠C=∠D时,可根据“ASA”判断△ABC≌△EBD,故正确;
D.当添加AC=DE时,无法判断△ABC≌△EBD,故错误;
故选:D.
2.D
解:A、因为,,又因为AD=AD,所以≌(SSS),故本选项不符合题意;
B、因为,,又因为AD=AD,所以≌(SAS),故本选项不符合题意;
C、因为,,又因为AD=AD,所以≌(AAS),故本选项不符合题意;
D、因为,,AD=AD,这是边边角,不能证明≌,故本选项符合题意.
故选:D.
3.D
解:AB=DC,AC=DB,BC=BC,
符合全等三角形的判定定理“SSS”,
能推出
,故A选项错误;
AB=DC,,BC=CB
符合全等三角形的判定定理“SAS”,
能推出
,故B选项错误;
在△AOB和△DOC中,
,
∴
(AAS),
∴AB=DC,∠ABO=∠DCO,
∵OB=OC,
∴∠OBC=∠OCB,
∴∠ABC=∠DCB,
在△ABC和△DCB中,
,
∴(SAS),
能推出,故C选项错误;
BC=CB,AB=DC,∠ACB=∠DBC,SSA不符合全等三角形的判定定理,即不能推出,故D选项正确.
故选D.
4.D
解:∵BE=CF,∴BC=EF,
又∵AB=DE,
A、添加BC=EF不能证明△ABC≌△DEF,故此选项错误;
B、添加∠A=∠D不能证明△ABC≌△DEF,故此选项错误;
C、添加AC∥DF可得∠ACB=∠F,不能证明△ABC≌△DEF,故此选项错误;
D、添加∠B=∠DEF可利用SAS判定△ABC≌△DEF,故此选项正确;
故选:D.
5.C
解:延长AP交BC于D,
∵BP平分∠ABC,AP⊥BP,
∴∠ABP=∠DBP,∠APB=∠DPB=90°,
在△ABP与△DBP中,
,
∴△ABP≌△DBP(ASA),
∴AP=PD,S△PBD=S△ABP
∴
∴S△ABD=10-4=6,
∴△ABP的面积=3cm2,
故选:C.
6.D
解:∵AD平分∠BAC,
∴∠BAD=∠CAD,
∵AB=AC,AD=AD,
∴△BAD≌△CAD(SAS),
∴BD=CD,故①符合题意;
∵∠B=∠C,AD=AD,
∴△BAD≌△CAD(AAS),
∴BD=CD,故②符合题意;
∵AD⊥BC,
∴∠ADB=∠ADC=90°,
∵AD=AD,
∴△BAD≌△CAD(ASA),
∴BD=DC,故③符合题意;
∵,
∴BD=DC,故④符合题意;
∴①②③④都可以得到BD=CD;
故选D.
7.C
解:∵AE=CF,
∴AE+EF=CF+EF,
∴AF=CE,
A、∠B=∠D,∠AFD=∠CEB,AF=CE,满足AAS,能判定△ADF≌△CBE;
B、BE=DF,∠AFD=∠CEB,AF=CE,满足SAS,能判定△ADF≌△CBE;
C、AD=CB,AF=CE,∠AFD=∠CEB,满足SSA,不能判定△ADF≌△CBE;
D、AD∥BC,则∠A=∠C,又AF=CE,∠AFD=∠CEB,满足ASA,能判定△ADF≌△CBE;
故选:C.
8.C
解:∵CB=CE.
∴当,时,满足SAS,可证△≌△,故A不符合题意;
当,时,满足SSS,可证△≌△,故B不符合题意;
当,时,满足是ASS,不能证明△≌△,故C符合题意;
当,时,满足AAS,可证△≌△,故D不符合题意.
故选C.
9.C
解:∵,
∴∠ACD+∠ECB=90?,
∵,,
∴∠ADC=∠CEB=90?,
∴∠ECB+∠CBE=90?,
∴∠ACD=∠CBE,
在△ACD和△CBE中,
∵∠ADC=∠CEB=90?,∠ACD=∠CBE,AC=BC,
∴△ACD≌△CBE(AAS),
∴AD=CE=6,CD=BE=2,
∴ED=EC-CD=6-2=4.
故选择:C.
10.B
解:如图,延长AP交BC于T.
∵BP⊥AT,
∴∠BPA=∠BPT=90°,
∵BP=BP,∠PBA=∠PBT,
∴△BPA≌△BPT(ASA),
∴PA=PT,
∴S△BPA=S△BPT,S△CAP=S△CPT,
∴S△PBC=S△ABC==0.5,
故选:B.
11.70°
解:
∵∠ABC=90°,
∴∠CBD=∠ABC
=90°,
在Rt△ABE与Rt△CBD中,
∴△ABE≌△CBD,
∴∠AEB=∠BDC,
∵AB=BC,
∴∠BAC=∠ACB=45°,
∵∠AEB为△AEC的外角,∠CAE=25°,
∴∠AEB=∠ACB+∠CAE=45°+25°=70°,
∴∠BDC=70°.
故答案为:70°.
12.∠B=∠B′或∠C=∠C′或AC=A′C′.
解:在△ABC和△A′B′C′中,AB=A′B′,∠A=∠A′,
当添加∠B=∠B′可利用“ASA”判断△ABC≌△A′B′C′;
当添加∠C=∠C′可利用“AAS”判断△ABC≌△A′B′C′;
当添加AC=∠A′C′可利用“SAS”判断△ABC≌△A′B′C′.
故答案为:∠B=∠B′或∠C=∠C′或AC=A′C′.
13.68°.
解:在△BDF和△CED中
∵BF=CD,∠B=∠C,BD=CE,
∴△BDF≌△CED(SAS),
∴∠BFD=∠CDE,∠BDF=∠CED,
∴∠BDF+∠CDE=180?-∠EDF=180?-56?=124?,
∴∠BFD+∠BDF=∠BDF+∠CDE=124?,
∴∠C=∠B=180?-∠BFD-∠BDF=56?,
∴∠A=180?-∠B-∠C=180?-56?-56?=68?.
故答案为:68?.
14.①②
解:在和中,
,
,
,①正确,
∴,
,
,
,②正确,
和中,只有一个条件,再没有其余条件可以证明
,故③④错误;
故答案是:①②.
15.2
或
3
解:设经过
t
秒后,使△BPD
与△CQP
全等.
∵AB=AC=12,点
D
为
AB
的中点.
∴BD=6.
∵∠ABC=∠ACB.
∴要使△BPD
与△CQP
全等,必须
BD=CP
或
BP=CP.
即
6=8﹣2t
或
2t=8﹣2t.
=1,=2.
当t=1
时,BP=CQ=2,2÷1=2.
当t=2
时,BD=CQ=6,6÷2=3.
即点
Q
的运动速度是
2
或
3,
故答案为:2
或
3.
16.解:(1)∵BF平分∠ABC,
∴,
∵CD∥AB,
∴,
∴,
∴BC=CE,
∴△BCE
是等腰三角形.
(2)∵CF平分∠BCE,
∴,
∵CD∥AB,
∴,
∴,
∴,即
CF⊥BE,
又BC=CE,
∴BF=EF,
在△ABF和△DEF中,
∵,
∴△ABF≌△DEF;
∴AB=DE,
∴BC=CE=DE+CD=AB+CD,
因此
BC=AB+CD.
17.
解:证明:∵BE=CF,
∴BE+EC=CF+EC,
∴BC=EF,
在△ABC和△DEF中,
∵,
∴△ABC
≌△DEF(SSS).
18.
解:证明:延长AD,BC交于点E.
∵CD⊥AD,
∴∠ADC=∠EDC=90°.
在△ADC和△EDC中
,
∴△ADC≌△EDC(ASA).
∴∠DAC=∠DEC,AC=EC,AD=ED.
∵AC=7,
∴EC=7.
∵BC=4
∴BE=11
∵∠DAB=∠B,
∴AE=BE=11.
∴AD=5.5.
答:AD的长为5.5.
19.
解:(1)证明:如图所示,连接DB.
∵AD是△ABC的外角平分线,DG⊥AB,DF⊥CA,
∴DF=DG.
∵DE垂直平分BC,
∴DC=DB,
在Rt△CDF与Rt△BDG中
∴Rt△CDF≌Rt△BDG(HL),
∴BG=CF.
(2)解:∵∠GAD=∠FAD,∠AGD=∠AFD,AD=AD,
∴在△ADG与△ADF中
∴△ADG≌△ADF(AAS),
∴AG=AF,
∵BG=CF
∴AG=(cm).
20.解:(1)证明:∵AD⊥MN,BE⊥MN,
∴∠ADC=∠CEB=90°,
∴∠DAC+∠ACD=90°,
∵∠ACB=90°,
∴∠BCE+∠ACD=90°,
∴∠DAC=∠BCE,
在△ADC和△CEB,
,
∴△ADC≌△CEB(AAS),
∴CD=BE,AD=CE,
∴DE=CE+CD=AD+BE;
(2)证明:∵AD⊥MN,BE⊥MN,
∴∠ADC=∠CEB=90°,
∴∠DAC+∠ACD=90°,
∵∠ACB=90°,
∴∠BCE+∠ACD=90°,
∴∠DAC=∠BCE,
∵AC=BC,
∴△ADC≌△CEB,
∴CD=BE,AD=CE,
∴DE=CE﹣CD=AD﹣BE;
(3)解:DE=BE﹣AD,理由如下:
∵AD⊥MN,BE⊥MN,
∴∠ADC=∠CEB=90°,
∴∠DAC+∠ACD=90°,
∵∠ACB=90°,
∴∠BCE+∠ACD=90°,
∴∠DAC=∠BCE,
∵AC=BC,
∴△ADC≌△CEB,
∴CD=BE,AD=CE,
∴DE=BE﹣AD.
