人教版九年级数学下册 27.2.1相似三角形的判定 课后练习二(Word版 含简单答案)
文档属性
| 名称 | 人教版九年级数学下册 27.2.1相似三角形的判定 课后练习二(Word版 含简单答案) |
|
|
| 格式 | zip | ||
| 文件大小 | 480.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-12-24 19:23:03 | ||
图片预览



文档简介
人教版九年级数学下册
第二十七章
相似
27.2.1相似三角形的判定
课后练习二
一、选择题
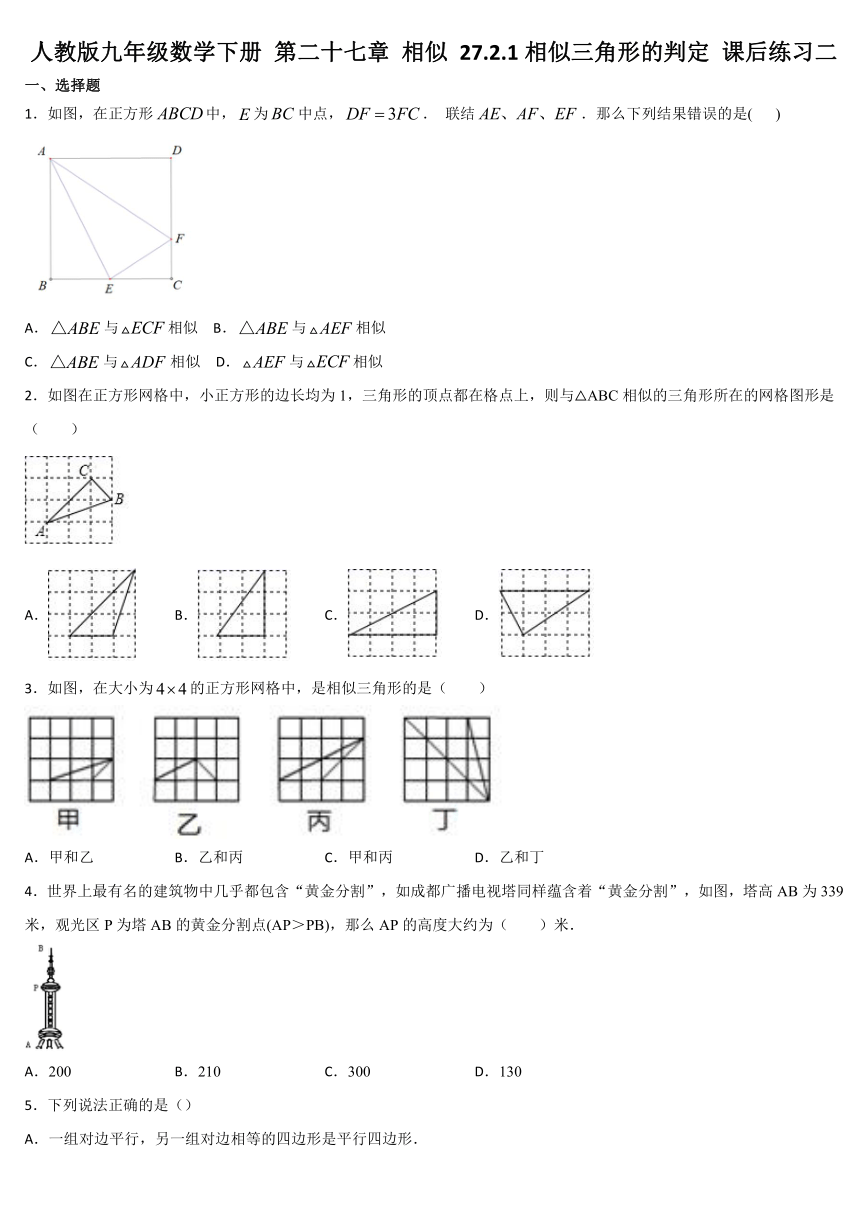
1.如图,在正方形中,为中点,.
联结.那么下列结果错误的是(
)
A.与相似
B.与相似
C.与相似
D.与相似
2.如图在正方形网格中,小正方形的边长均为1,三角形的顶点都在格点上,则与△ABC相似的三角形所在的网格图形是( )
A.
B.
C.
D.
3.如图,在大小为的正方形网格中,是相似三角形的是(
)
A.甲和乙
B.乙和丙
C.甲和丙
D.乙和丁
4.世界上最有名的建筑物中几乎都包含“黄金分割”,如成都广播电视塔同样蕴含着“黄金分割”,如图,塔高AB为339米,观光区P为塔AB的黄金分割点(AP>PB),那么AP的高度大约为(
)米.
A.200
B.210
C.300
D.130
5.下列说法正确的是()
A.一组对边平行,另一组对边相等的四边形是平行四边形.
B.有一角为65°的两个等腰三角形相似.
C.顺次连接一个四边形各边中点所得到的四边形是矩形,那么原四边形一定是菱形.
D.对角线互相垂直平分的四边形是菱形.
6.如图,正方形,点、分别在边、上,且,把绕点沿逆时针方向旋转90°得到,连接交、于点、,连接,并在截取,连接.有如下结论:
①;②始终平分;③;④;⑤垂直平分.
上述结论中,所有正确的个数是(
)
A.5个
B.4个
C.3个
D.2个
7.如图,△ABC中∠A=60°,AB=4,AC=6,将△ABC沿图示中的虚线剪开,剪下的三角形与△ABC不相似的是(
)
A.
B.
C.
D.
8.如图,已知△ABC和△ADE均为等边三角形,点D在BC边上,DE与AC相交于点F,图中相似的三角形有( )对.
A.3
B.4
C.5
D.6
9.如图,在中,点分别在边、上.
则在下列五个条件中:①;②;③;④;⑤,能满足的条件有(
)
A.2个
B.3个
C.4个
D.5个
10.下列命题中,正确的是(
)
A.两个等腰三角形一定相似
B.两个含角的等腰三角形一定相似
C.两个含角的等腰三角形一定相似
D.两个含角的等腰三角形一定相似
二、填空题
11.如图,在矩形ABCD中,,,动点M从点A出发,沿AB以的速度向点B匀速运动,运动到点B时停止运动,同时动点N从点D出发,沿DA以的速度向点A勾速运动,运动到点A时停止运动.若与相似,则运动的时间t为______.
12.在中,,,D是AC上一点,,在AB上取一点E,使A、D、E三点组成的三角形与相似,则AE的长为_______.
13.如图,正方形的边长为2,连接,点是线段延长线上的一个动点,,点是与线段延长线的交点,当平分时,______(填“>”“<”或“=”):当不平分时,__________.
14.如图,、是的边上的两点,以为边作平行四边形,经过点,且.试写出四对相似三角形________.
15.点是的边上一点,过点的直线与的边界的另一个交点为,则使与相似的直线可能有________(把正确的结论的代号都填上).
①条;②条;③条;④条.
三、解答题
16.如图,直线与轴、轴分别相交于、两点,抛物线经过点,交轴正半轴于点.
(1)求该抛物线的函数表达式;
(2)已知点是抛物线上的一个动点,并且点在第一象限内,连接、,设点的横坐标为,的面积为,求与的函数表达式,并求出的最大值及此时动点的坐标;
(3)将点绕原点旋转得点,连接、,在旋转过程中,一动点从点出发,沿线段以每秒个单位的速度运动到,再沿线段以每秒个单位长度的速度运动到后停止,求点在整个运动过程中用时最少是多少?
17.如图1,在正方形ABCD中,对角线AC、BD交于点O,点E在AB上,点F在BC的延长线上,且AE=CF,连接EF交AC于点P,分别连接DE,DF,DP
(1)求证:△ADE≌△CDF;
(2)求证:△ADP∽△BDF;
(3)如图2,若PE=BE,PC=,求CF的值.
18.如图,已知,它们依次交直线,,,于点A、B、C和点D、E、F,,.
(1)求AB、BC的长;
(2)当,时,求BE的长.
19.如图,在中,,,垂足为点,点是上的一点,连接,作,且交于点.
(1)求证:;
(2)除(1)中的相似三角形外,图中还有其它的相似三角形吗?若有,请将它们全部直接写出来.
20.已知△ABC中,AB=AC,∠BAC=90°,点D是平面内一点;
(1)如图1,
BD⊥CD,∠DCA=30°,则∠BAD=
(2)如图2,若∠BDC=45°,点F是CD中点,求证:AF⊥CD;
(3)如图3,∠BDA=3∠CBD,BD=,求△BCD的面积.
21.如图1,若顺次连接四边形ABCD各边中点得的四边形EFGH是矩形,则称原四边形ABCD为“中母矩形”即若四边形的对角线互相垂直,那么这个四边形称为“中母矩形”.
(1)如图2,在直角坐标系xOy中,已知A(4,0),B(1,4),C(4,6),请在格点上标出D点的位置(只标一点即可),使四边形ABCD是中母矩形.并写出点D的坐标.
(2)如图3,以△ABC的边AB,AC为边,向三角形外作正方形ABDE及ACFG,连接CE,BG相交于点O,试判断四边形BEGC是中母矩形?说明理由.
(3)如图4,在Rt△ABC中,AB=8,BC=6,E是斜边AC的中点,F是直角边AB的中点,P是直角边BC上一动点,试探究:当PC=_____时,四边形BPEF是中母矩形?(直角三角形中,30°角所对的直角边是斜边的一半)
22.二次函数
(1)画出上述二次函数的图象;
(2)如图,二次函数的图象与x轴的其中一个交点是B,与y轴的交点是C,直线BC与反比例函数的图象交于点D,且BC=3CD,求反比例函数的解析式.
(3)在(2)的条件下,x轴上的点P的横坐标是多少时,△BCP与△OCD相似.
23.已知,,,是的中点,是平面上的一点,且,连接.
(1)如图,当点在线段上时,求的长;
(2)当是等腰三角形时,求的长;
(3)将点绕点顺时针旋转得到点,连接,求的最大值.
【参考答案】
1.C
2.C
3.C
4.B
5.D
6.B
7.A
8.C
9.B
10.D
11.1.5s或2.4s
12.8或
13.=
8
14.;;;
15.④
16.(1);(2),的最大值是,此时动点的坐标是;(3)秒.
17.(1)路(2)略;(3)CF=﹣1,
18.(1)
;BC=6;(2)BE=9.
19.(1)略析;(2);
;
;
.
20.(1)15°;(2)略;(3).
21.(1)略,D(6,4);(2)略;(3).
22.(1)略;(2);(3)P的横坐标为5或12时,ΔBCP∽ΔOCD.
23.(1)2;(2)略;(3)
.
第二十七章
相似
27.2.1相似三角形的判定
课后练习二
一、选择题
1.如图,在正方形中,为中点,.
联结.那么下列结果错误的是(
)
A.与相似
B.与相似
C.与相似
D.与相似
2.如图在正方形网格中,小正方形的边长均为1,三角形的顶点都在格点上,则与△ABC相似的三角形所在的网格图形是( )
A.
B.
C.
D.
3.如图,在大小为的正方形网格中,是相似三角形的是(
)
A.甲和乙
B.乙和丙
C.甲和丙
D.乙和丁
4.世界上最有名的建筑物中几乎都包含“黄金分割”,如成都广播电视塔同样蕴含着“黄金分割”,如图,塔高AB为339米,观光区P为塔AB的黄金分割点(AP>PB),那么AP的高度大约为(
)米.
A.200
B.210
C.300
D.130
5.下列说法正确的是()
A.一组对边平行,另一组对边相等的四边形是平行四边形.
B.有一角为65°的两个等腰三角形相似.
C.顺次连接一个四边形各边中点所得到的四边形是矩形,那么原四边形一定是菱形.
D.对角线互相垂直平分的四边形是菱形.
6.如图,正方形,点、分别在边、上,且,把绕点沿逆时针方向旋转90°得到,连接交、于点、,连接,并在截取,连接.有如下结论:
①;②始终平分;③;④;⑤垂直平分.
上述结论中,所有正确的个数是(
)
A.5个
B.4个
C.3个
D.2个
7.如图,△ABC中∠A=60°,AB=4,AC=6,将△ABC沿图示中的虚线剪开,剪下的三角形与△ABC不相似的是(
)
A.
B.
C.
D.
8.如图,已知△ABC和△ADE均为等边三角形,点D在BC边上,DE与AC相交于点F,图中相似的三角形有( )对.
A.3
B.4
C.5
D.6
9.如图,在中,点分别在边、上.
则在下列五个条件中:①;②;③;④;⑤,能满足的条件有(
)
A.2个
B.3个
C.4个
D.5个
10.下列命题中,正确的是(
)
A.两个等腰三角形一定相似
B.两个含角的等腰三角形一定相似
C.两个含角的等腰三角形一定相似
D.两个含角的等腰三角形一定相似
二、填空题
11.如图,在矩形ABCD中,,,动点M从点A出发,沿AB以的速度向点B匀速运动,运动到点B时停止运动,同时动点N从点D出发,沿DA以的速度向点A勾速运动,运动到点A时停止运动.若与相似,则运动的时间t为______.
12.在中,,,D是AC上一点,,在AB上取一点E,使A、D、E三点组成的三角形与相似,则AE的长为_______.
13.如图,正方形的边长为2,连接,点是线段延长线上的一个动点,,点是与线段延长线的交点,当平分时,______(填“>”“<”或“=”):当不平分时,__________.
14.如图,、是的边上的两点,以为边作平行四边形,经过点,且.试写出四对相似三角形________.
15.点是的边上一点,过点的直线与的边界的另一个交点为,则使与相似的直线可能有________(把正确的结论的代号都填上).
①条;②条;③条;④条.
三、解答题
16.如图,直线与轴、轴分别相交于、两点,抛物线经过点,交轴正半轴于点.
(1)求该抛物线的函数表达式;
(2)已知点是抛物线上的一个动点,并且点在第一象限内,连接、,设点的横坐标为,的面积为,求与的函数表达式,并求出的最大值及此时动点的坐标;
(3)将点绕原点旋转得点,连接、,在旋转过程中,一动点从点出发,沿线段以每秒个单位的速度运动到,再沿线段以每秒个单位长度的速度运动到后停止,求点在整个运动过程中用时最少是多少?
17.如图1,在正方形ABCD中,对角线AC、BD交于点O,点E在AB上,点F在BC的延长线上,且AE=CF,连接EF交AC于点P,分别连接DE,DF,DP
(1)求证:△ADE≌△CDF;
(2)求证:△ADP∽△BDF;
(3)如图2,若PE=BE,PC=,求CF的值.
18.如图,已知,它们依次交直线,,,于点A、B、C和点D、E、F,,.
(1)求AB、BC的长;
(2)当,时,求BE的长.
19.如图,在中,,,垂足为点,点是上的一点,连接,作,且交于点.
(1)求证:;
(2)除(1)中的相似三角形外,图中还有其它的相似三角形吗?若有,请将它们全部直接写出来.
20.已知△ABC中,AB=AC,∠BAC=90°,点D是平面内一点;
(1)如图1,
BD⊥CD,∠DCA=30°,则∠BAD=
(2)如图2,若∠BDC=45°,点F是CD中点,求证:AF⊥CD;
(3)如图3,∠BDA=3∠CBD,BD=,求△BCD的面积.
21.如图1,若顺次连接四边形ABCD各边中点得的四边形EFGH是矩形,则称原四边形ABCD为“中母矩形”即若四边形的对角线互相垂直,那么这个四边形称为“中母矩形”.
(1)如图2,在直角坐标系xOy中,已知A(4,0),B(1,4),C(4,6),请在格点上标出D点的位置(只标一点即可),使四边形ABCD是中母矩形.并写出点D的坐标.
(2)如图3,以△ABC的边AB,AC为边,向三角形外作正方形ABDE及ACFG,连接CE,BG相交于点O,试判断四边形BEGC是中母矩形?说明理由.
(3)如图4,在Rt△ABC中,AB=8,BC=6,E是斜边AC的中点,F是直角边AB的中点,P是直角边BC上一动点,试探究:当PC=_____时,四边形BPEF是中母矩形?(直角三角形中,30°角所对的直角边是斜边的一半)
22.二次函数
(1)画出上述二次函数的图象;
(2)如图,二次函数的图象与x轴的其中一个交点是B,与y轴的交点是C,直线BC与反比例函数的图象交于点D,且BC=3CD,求反比例函数的解析式.
(3)在(2)的条件下,x轴上的点P的横坐标是多少时,△BCP与△OCD相似.
23.已知,,,是的中点,是平面上的一点,且,连接.
(1)如图,当点在线段上时,求的长;
(2)当是等腰三角形时,求的长;
(3)将点绕点顺时针旋转得到点,连接,求的最大值.
【参考答案】
1.C
2.C
3.C
4.B
5.D
6.B
7.A
8.C
9.B
10.D
11.1.5s或2.4s
12.8或
13.=
8
14.;;;
15.④
16.(1);(2),的最大值是,此时动点的坐标是;(3)秒.
17.(1)路(2)略;(3)CF=﹣1,
18.(1)
;BC=6;(2)BE=9.
19.(1)略析;(2);
;
;
.
20.(1)15°;(2)略;(3).
21.(1)略,D(6,4);(2)略;(3).
22.(1)略;(2);(3)P的横坐标为5或12时,ΔBCP∽ΔOCD.
23.(1)2;(2)略;(3)
.
