北师大版数学九年级上册 6.2反比例函数的图像与性质 综合提升练习(word版无答案)
文档属性
| 名称 | 北师大版数学九年级上册 6.2反比例函数的图像与性质 综合提升练习(word版无答案) |  | |
| 格式 | zip | ||
| 文件大小 | 92.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-12-24 20:09:14 | ||
图片预览

文档简介
【6.2反比例函数的图像与性质】综合提升练习(一)
一.选择题
1.已知反比例函数y=﹣(a﹣1)的图象位于第一、三象限,则a的值为( )
A.6
B.﹣1
C.﹣1或6
D.﹣6或1
2.如果反比例函数y=(a是常数)的图象在第二、四象限,那么a的取值范围是( )
A.a>2
B.a<2
C.a>0
D.a<0
3.下列函数中,其图象经过原点的是( )
A.y=2x﹣3
B.y=
C.y=x2﹣1
D.y=
4.如图,点A是反比例函数y=图象上的一点,AB垂直x轴于点B,若S△ABO=2.5,则k的值为( )
A.2.5
B.5
C.﹣5
D.﹣2.5
5.如图,在平面直角坐标系中,函数y=(k>0,x>0)的图象与等边三角形OAB的边OA,AB分别交于点M,N,且OM=2MA,若AB=3,那么点N的横坐标为( )
A.
B.
C.4
D.6
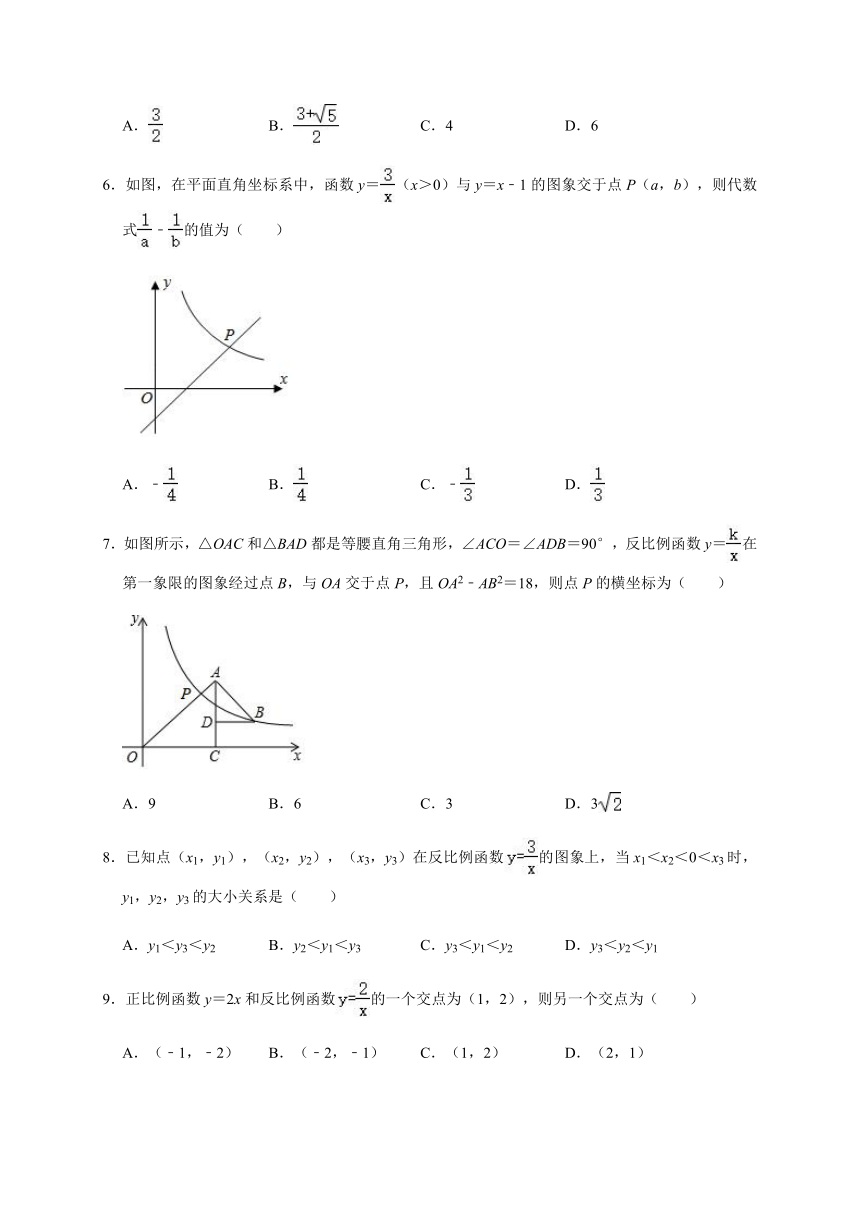
6.如图,在平面直角坐标系中,函数y=(x>0)与y=x﹣1的图象交于点P(a,b),则代数式﹣的值为( )
A.﹣
B.
C.﹣
D.
7.如图所示,△OAC和△BAD都是等腰直角三角形,∠ACO=∠ADB=90°,反比例函数y=在第一象限的图象经过点B,与OA交于点P,且OA2﹣AB2=18,则点P的横坐标为( )
A.9
B.6
C.3
D.3
8.已知点(x1,y1),(x2,y2),(x3,y3)在反比例函数的图象上,当x1<x2<0<x3时,y1,y2,y3的大小关系是( )
A.y1<y3<y2
B.y2<y1<y3
C.y3<y1<y2
D.y3<y2<y1
9.正比例函数y=2x和反比例函数的一个交点为(1,2),则另一个交点为( )
A.(﹣1,﹣2)
B.(﹣2,﹣1)
C.(1,2)
D.(2,1)
10.如图,函数y=kx(k>0)与函数y=的图象相交于A,C两点,过A作AB⊥y轴于B,连结BC,则三角形ABC的面积为( )
A.1
B.2
C.k2
D.2k2
二.填空题
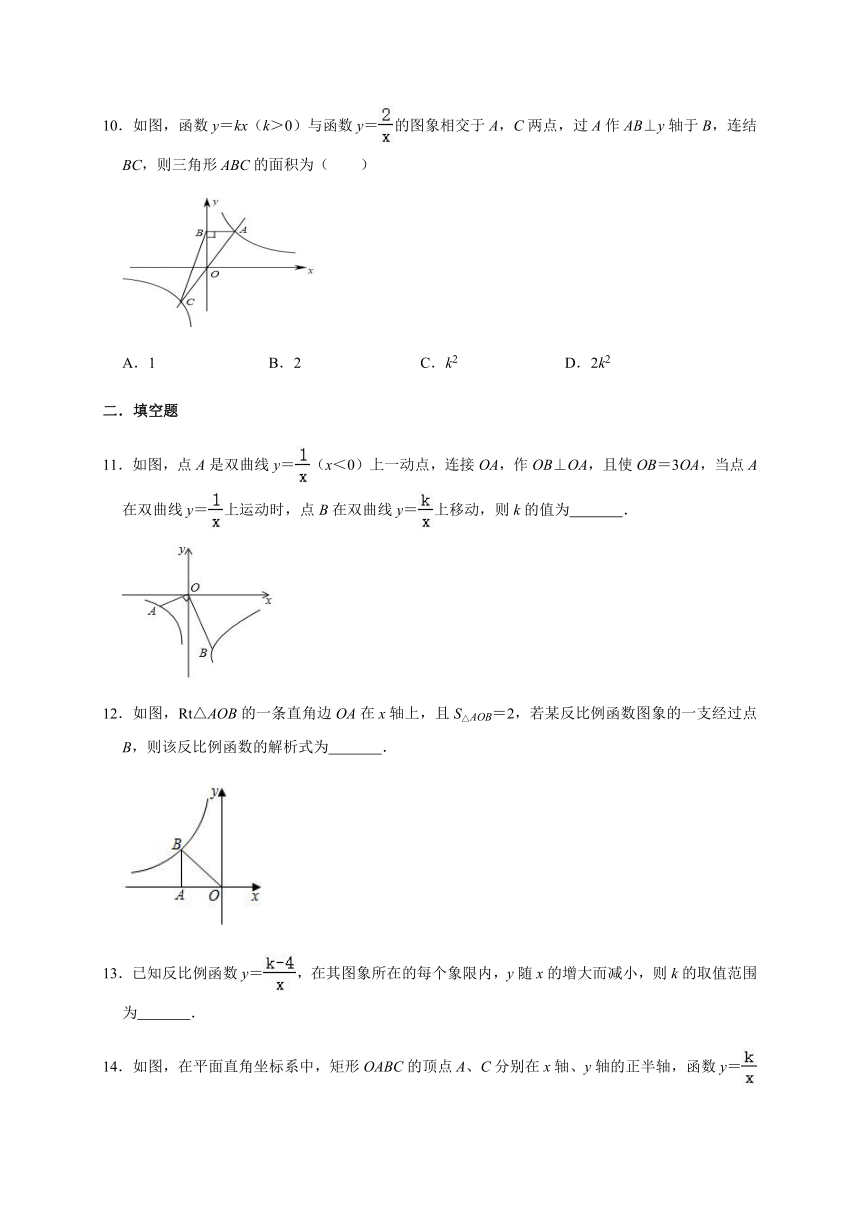
11.如图,点A是双曲线y=(x<0)上一动点,连接OA,作OB⊥OA,且使OB=3OA,当点A在双曲线y=上运动时,点B在双曲线y=上移动,则k的值为
.
12.如图,Rt△AOB的一条直角边OA在x轴上,且S△AOB=2,若某反比例函数图象的一支经过点B,则该反比例函数的解析式为
.
13.已知反比例函数y=,在其图象所在的每个象限内,y随x的增大而减小,则k的取值范围为
.
14.如图,在平面直角坐标系中,矩形OABC的顶点A、C分别在x轴、y轴的正半轴,函数y=(k>0,x>0)交BC于点D,交AB于点E.若BD=2CD,S四边形ODBE=4,则k的值为
.
15.如图,P是反比例函数y=图象上的一点,过点P向x轴作垂线交于点A,连接OP.若图中阴影部分的面积是1,则此反比例函数的解析式为
.
三.解答题
16.在平面直角坐标系中,如果C(x1,y1),D(x2,y2),那么CD两点间的距离可以用|CD|=来计算.如图,已知点A(﹣,0),B(0,),N(O,3),P为反比例函数y=﹣(x<0)的图象上一动点,PM与x轴平行且与直线AB交于点M.
(1)如果点F的坐标为F(﹣,),试比较|PF|与|PM|的大小关系.
(2)求|PM|+|PN|的最小值.
17.如图,在平面直角坐标系中,一次函数y1=kx+b(k≠0)的图象与反比例函数的图象相交于第一、三象限内的A(3,5),B(a,﹣3)两点,与x轴交于点C.
(1)求该反比例函数和一次函数的解析式;
(2)直接写出当y1>y2时,x的取值范围;
(3)在y轴上找一点P使PB﹣PC最大,求PB﹣PC的最大值及点P的坐标.
18.已知一次函数y1=3x﹣3的图象与反比例函数的图象交于点A(a,3),B(﹣1,b).
(1)求a,b的值和反比例函数的表达式.
(2)设点P(h,y1),Q(h,y2)分别是两函数图象上的点.
①试直接写出当y1>y2时h的取值范围;
②若y2﹣y1=3,试求h的值.
19.如图,在平面直角坐标系xOy中,一次函数y=ax+b(a≠0)的图象与反比例函数y=(k≠0,x>0)的图象相交于A(1,5),B(m,1)两点,与x轴,y轴分别交于点C,D,连接OA,OB.
(1)求反比例函数y=(k≠0,x>0)和一次函数y=ax+b(a≠0)的表达式;
(2)求△AOB的面积.
20.如图,在平面直角坐标系xOy中,正方形OABC的边长为2,函数y=(x>0)的图象经过点B,与直线y=x+b交于点D.
(1)求k的值;
(2)直线y=x+b与BC边所在直线交于点M,与x轴交于点N.
①当点D为MN中点时,求b的值;
②当DM>MN时,结合函数图象,直接写出b的取值范围.
一.选择题
1.已知反比例函数y=﹣(a﹣1)的图象位于第一、三象限,则a的值为( )
A.6
B.﹣1
C.﹣1或6
D.﹣6或1
2.如果反比例函数y=(a是常数)的图象在第二、四象限,那么a的取值范围是( )
A.a>2
B.a<2
C.a>0
D.a<0
3.下列函数中,其图象经过原点的是( )
A.y=2x﹣3
B.y=
C.y=x2﹣1
D.y=
4.如图,点A是反比例函数y=图象上的一点,AB垂直x轴于点B,若S△ABO=2.5,则k的值为( )
A.2.5
B.5
C.﹣5
D.﹣2.5
5.如图,在平面直角坐标系中,函数y=(k>0,x>0)的图象与等边三角形OAB的边OA,AB分别交于点M,N,且OM=2MA,若AB=3,那么点N的横坐标为( )
A.
B.
C.4
D.6
6.如图,在平面直角坐标系中,函数y=(x>0)与y=x﹣1的图象交于点P(a,b),则代数式﹣的值为( )
A.﹣
B.
C.﹣
D.
7.如图所示,△OAC和△BAD都是等腰直角三角形,∠ACO=∠ADB=90°,反比例函数y=在第一象限的图象经过点B,与OA交于点P,且OA2﹣AB2=18,则点P的横坐标为( )
A.9
B.6
C.3
D.3
8.已知点(x1,y1),(x2,y2),(x3,y3)在反比例函数的图象上,当x1<x2<0<x3时,y1,y2,y3的大小关系是( )
A.y1<y3<y2
B.y2<y1<y3
C.y3<y1<y2
D.y3<y2<y1
9.正比例函数y=2x和反比例函数的一个交点为(1,2),则另一个交点为( )
A.(﹣1,﹣2)
B.(﹣2,﹣1)
C.(1,2)
D.(2,1)
10.如图,函数y=kx(k>0)与函数y=的图象相交于A,C两点,过A作AB⊥y轴于B,连结BC,则三角形ABC的面积为( )
A.1
B.2
C.k2
D.2k2
二.填空题
11.如图,点A是双曲线y=(x<0)上一动点,连接OA,作OB⊥OA,且使OB=3OA,当点A在双曲线y=上运动时,点B在双曲线y=上移动,则k的值为
.
12.如图,Rt△AOB的一条直角边OA在x轴上,且S△AOB=2,若某反比例函数图象的一支经过点B,则该反比例函数的解析式为
.
13.已知反比例函数y=,在其图象所在的每个象限内,y随x的增大而减小,则k的取值范围为
.
14.如图,在平面直角坐标系中,矩形OABC的顶点A、C分别在x轴、y轴的正半轴,函数y=(k>0,x>0)交BC于点D,交AB于点E.若BD=2CD,S四边形ODBE=4,则k的值为
.
15.如图,P是反比例函数y=图象上的一点,过点P向x轴作垂线交于点A,连接OP.若图中阴影部分的面积是1,则此反比例函数的解析式为
.
三.解答题
16.在平面直角坐标系中,如果C(x1,y1),D(x2,y2),那么CD两点间的距离可以用|CD|=来计算.如图,已知点A(﹣,0),B(0,),N(O,3),P为反比例函数y=﹣(x<0)的图象上一动点,PM与x轴平行且与直线AB交于点M.
(1)如果点F的坐标为F(﹣,),试比较|PF|与|PM|的大小关系.
(2)求|PM|+|PN|的最小值.
17.如图,在平面直角坐标系中,一次函数y1=kx+b(k≠0)的图象与反比例函数的图象相交于第一、三象限内的A(3,5),B(a,﹣3)两点,与x轴交于点C.
(1)求该反比例函数和一次函数的解析式;
(2)直接写出当y1>y2时,x的取值范围;
(3)在y轴上找一点P使PB﹣PC最大,求PB﹣PC的最大值及点P的坐标.
18.已知一次函数y1=3x﹣3的图象与反比例函数的图象交于点A(a,3),B(﹣1,b).
(1)求a,b的值和反比例函数的表达式.
(2)设点P(h,y1),Q(h,y2)分别是两函数图象上的点.
①试直接写出当y1>y2时h的取值范围;
②若y2﹣y1=3,试求h的值.
19.如图,在平面直角坐标系xOy中,一次函数y=ax+b(a≠0)的图象与反比例函数y=(k≠0,x>0)的图象相交于A(1,5),B(m,1)两点,与x轴,y轴分别交于点C,D,连接OA,OB.
(1)求反比例函数y=(k≠0,x>0)和一次函数y=ax+b(a≠0)的表达式;
(2)求△AOB的面积.
20.如图,在平面直角坐标系xOy中,正方形OABC的边长为2,函数y=(x>0)的图象经过点B,与直线y=x+b交于点D.
(1)求k的值;
(2)直线y=x+b与BC边所在直线交于点M,与x轴交于点N.
①当点D为MN中点时,求b的值;
②当DM>MN时,结合函数图象,直接写出b的取值范围.
同课章节目录
- 第一章 特殊平行四边形
- 1 菱形的性质与判定
- 2 矩形的性质与判定
- 3 正方形的性质与判定
- 第二章 一元二次方程
- 1 认识一元二次方程
- 2 用配方法求解一元二次方程
- 3 用公式法求解一元二次方程
- 4 用因式分解法求解一元二次方程
- 5 一元二次方程的根与系数的关系
- 6 应用一元二次方程
- 第三章 概率的进一步认识
- 1 用树状图或表格求概率
- 2 用频率估计概率
- 第四章 图形的相似
- 1 成比例线段
- 2 平行线分线段成比例
- 3 相似多边形
- 4 探索三角形相似的条件
- 5 相似三角形判定定理的证明
- 6 利用相似三角形测高
- 7 相似三角形的性质
- 8 图形的位似
- 第五章 投影与视图
- 1 投影
- 2 视图
- 第六章 反比例函数
- 1 反比例函数
- 2 反比例函数的图象与性质
- 3 反比例函数的应用
