12.3.1等腰三角形(1)
文档属性
| 名称 | 12.3.1等腰三角形(1) |

|
|
| 格式 | rar | ||
| 文件大小 | 152.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2011-11-17 00:00:00 | ||
图片预览


文档简介
(共16张PPT)
演示
B
C
D
A
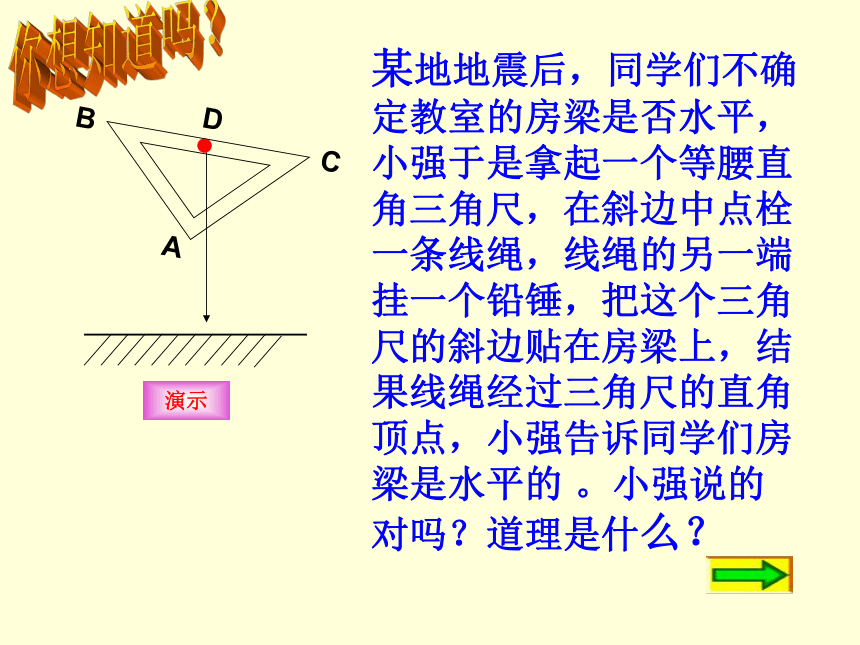
某地地震后,同学们不确定教室的房梁是否水平,小强于是拿起一个等腰直角三角尺,在斜边中点栓一条线绳,线绳的另一端挂一个铅锤,把这个三角尺的斜边贴在房梁上,结果线绳经过三角尺的直角顶点,小强告诉同学们房梁是水平的 。小强说的对吗?道理是什么?
相关概念:
定义:两条边相等的三角形叫做等腰三角形。
边:等腰三角形中,相等的两条边叫做腰,
腰
腰
另一条边叫做底边.
底
腰
腰
底
相关概念:
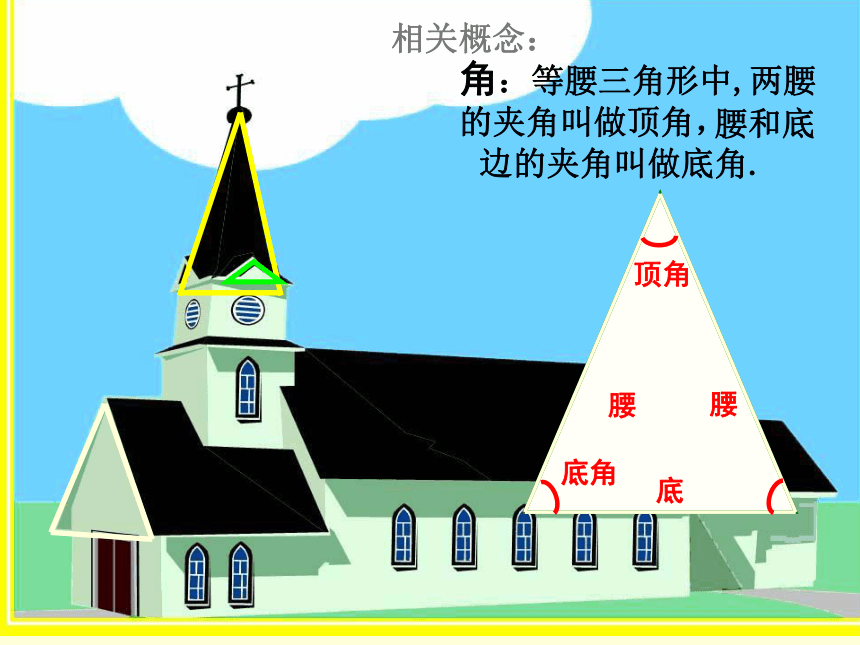
角:等腰三角形中,两腰的夹角叫做顶角,
顶角
腰和底边的夹角叫做底角.
底角
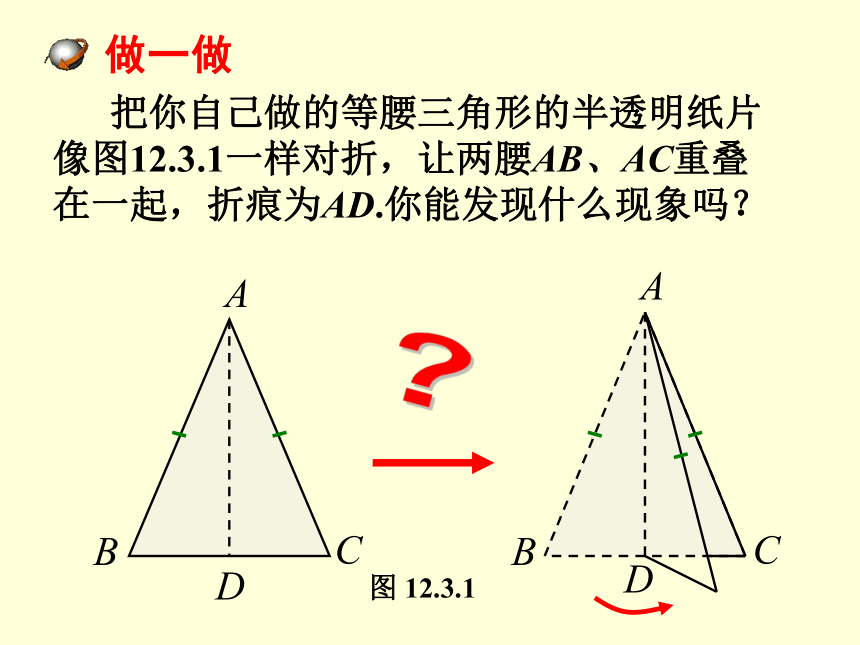
把你自己做的等腰三角形的半透明纸片像图12.3.1一样对折,让两腰AB、AC重叠在一起,折痕为AD.你能发现什么现象吗?
图 12.3.1
做一做
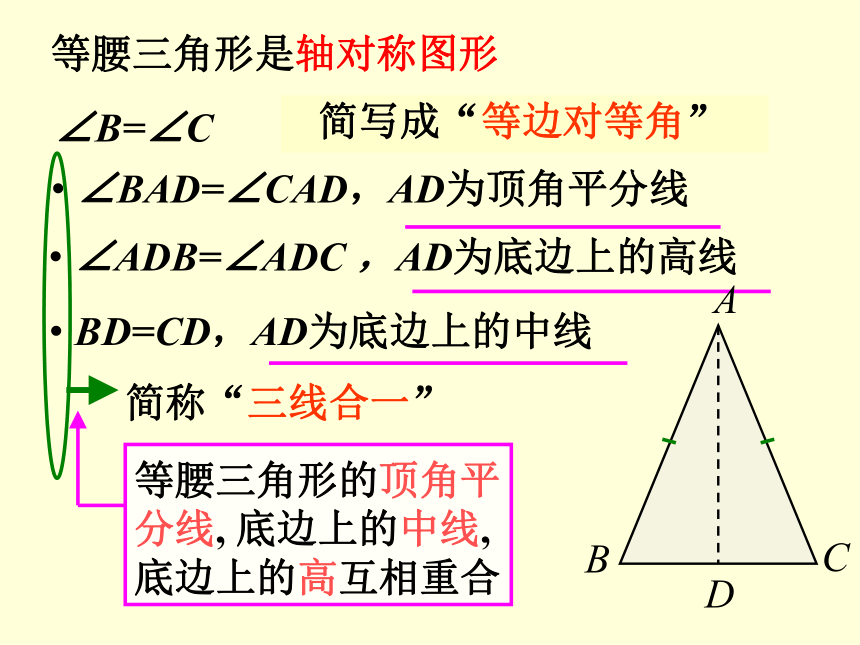
等腰三角形是轴对称图形
∠B=∠C
等腰三角形两个底角相等
简写成“等边对等角”
BD=CD,AD为底边上的中线
∠ADB=∠ADC ,AD为底边上的高线
∠BAD=∠CAD,AD为顶角平分线
等腰三角形的顶角平分线, 底边上的中线,底边上的高互相重合
简称“三线合一”
·→ 画出任意一个等腰三角形的底角平分线、腰上的中线和高,看看它们是否重合?
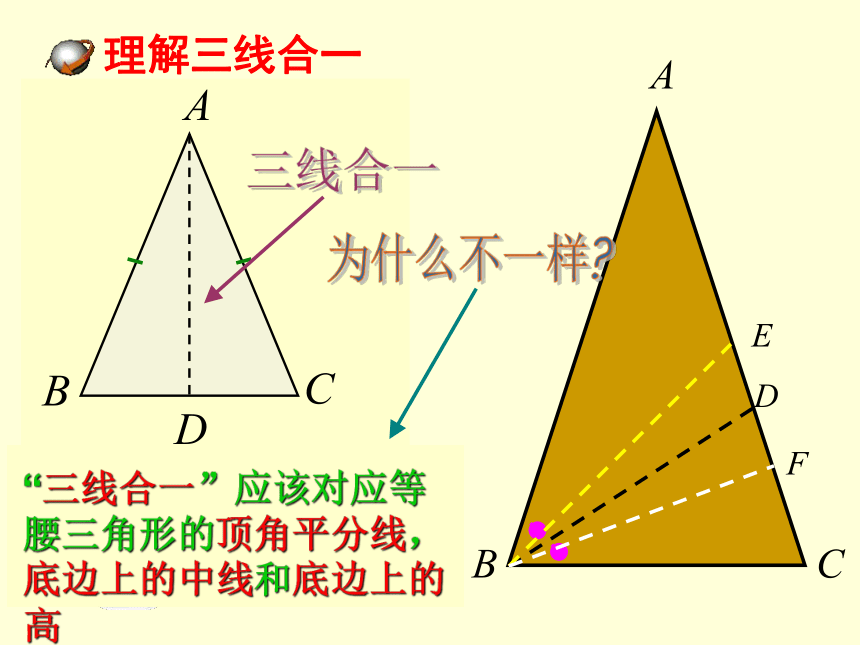
“三线合一”应该对应等腰三角形的顶角平分线,底边上的中线和底边上的高
理解三线合一
1. 等腰三角形是轴对称图形
2. 等腰三角形两个底角相等,简写成“等边对等角”
3. 等腰三角形的顶角平分线、底边上的中线、底边上的高 互相重合简称“三线合一”
小组合作证明等腰三角形的性质(比一比谁的方法多)
解:过点A做∠BAC的平分线AD,AD和BC相交于点D.
在△ABD与△ACD中,
AB=AC(已知)
∠BAD=∠CAD
AD=AD(公共边)
所以△ABD≌△ACD(S.A.S)
所以∠B=∠C(全等三角形的对应角相等)
A
B D C
因为AD平分∠BAC(已知),
所以∠BAD=∠CAD(角平分线的意义)
如图,在△ABC中,已知AB=AC,说明∠B=∠C的理由
已知: ABC中,AB=AC,
求证: B= C
证明:作底边上的高AD .
B D C
1 2
1= 2=90
在Rt BAD和Rt CAD中,
AB=AC(已知)
AD=AD(公共边)
所以△ABD≌△ACD(HL)
所以∠B=∠C(全等三角形的对应角相等)
证明:作底边上的中线 AD。
已知: ABC中,AB=AC,求证: B= C
A
B D C
在 BAD和 CAD中,
AB=AC(已知)
BD=CD(辅助线作法)
AD=AD(公共边)
所以△ABD≌△ACD(S.S.S)
所以∠B=∠C(全等三角形的对应角相等)
1.在等腰△ABC中,AB =AC, ∠A = 50°,
则∠B =_____,∠C=______
变式练习:1、在等腰中,∠A =50°, 则
∠B =___,∠C=___
2、在等腰中,∠A =100°, 则
∠B =___,∠C=___
C
B
A
C
B
A
C
B
A
(变式1①) (变式1② (变式1③)
(变式1①) (变式1②) (变式1③)
演示
B
C
D
A
某地地震后,同学们不确定教室的房梁是否水平,小强于是拿起一个等腰直角三角尺,在斜边中点栓一条线绳,线绳的另一端挂一个铅锤,把这个三角尺的斜边贴在房梁上,结果线绳经过三角尺的直角顶点,小强告诉同学们房梁是水平的 。小强说的对吗?道理是什么?
在数学的天地里,重要的不是我们知道什么,而是我们怎么知道什么。
——毕达哥拉斯
演示
B
C
D
A
某地地震后,同学们不确定教室的房梁是否水平,小强于是拿起一个等腰直角三角尺,在斜边中点栓一条线绳,线绳的另一端挂一个铅锤,把这个三角尺的斜边贴在房梁上,结果线绳经过三角尺的直角顶点,小强告诉同学们房梁是水平的 。小强说的对吗?道理是什么?
相关概念:
定义:两条边相等的三角形叫做等腰三角形。
边:等腰三角形中,相等的两条边叫做腰,
腰
腰
另一条边叫做底边.
底
腰
腰
底
相关概念:
角:等腰三角形中,两腰的夹角叫做顶角,
顶角
腰和底边的夹角叫做底角.
底角
把你自己做的等腰三角形的半透明纸片像图12.3.1一样对折,让两腰AB、AC重叠在一起,折痕为AD.你能发现什么现象吗?
图 12.3.1
做一做
等腰三角形是轴对称图形
∠B=∠C
等腰三角形两个底角相等
简写成“等边对等角”
BD=CD,AD为底边上的中线
∠ADB=∠ADC ,AD为底边上的高线
∠BAD=∠CAD,AD为顶角平分线
等腰三角形的顶角平分线, 底边上的中线,底边上的高互相重合
简称“三线合一”
·→ 画出任意一个等腰三角形的底角平分线、腰上的中线和高,看看它们是否重合?
“三线合一”应该对应等腰三角形的顶角平分线,底边上的中线和底边上的高
理解三线合一
1. 等腰三角形是轴对称图形
2. 等腰三角形两个底角相等,简写成“等边对等角”
3. 等腰三角形的顶角平分线、底边上的中线、底边上的高 互相重合简称“三线合一”
小组合作证明等腰三角形的性质(比一比谁的方法多)
解:过点A做∠BAC的平分线AD,AD和BC相交于点D.
在△ABD与△ACD中,
AB=AC(已知)
∠BAD=∠CAD
AD=AD(公共边)
所以△ABD≌△ACD(S.A.S)
所以∠B=∠C(全等三角形的对应角相等)
A
B D C
因为AD平分∠BAC(已知),
所以∠BAD=∠CAD(角平分线的意义)
如图,在△ABC中,已知AB=AC,说明∠B=∠C的理由
已知: ABC中,AB=AC,
求证: B= C
证明:作底边上的高AD .
B D C
1 2
1= 2=90
在Rt BAD和Rt CAD中,
AB=AC(已知)
AD=AD(公共边)
所以△ABD≌△ACD(HL)
所以∠B=∠C(全等三角形的对应角相等)
证明:作底边上的中线 AD。
已知: ABC中,AB=AC,求证: B= C
A
B D C
在 BAD和 CAD中,
AB=AC(已知)
BD=CD(辅助线作法)
AD=AD(公共边)
所以△ABD≌△ACD(S.S.S)
所以∠B=∠C(全等三角形的对应角相等)
1.在等腰△ABC中,AB =AC, ∠A = 50°,
则∠B =_____,∠C=______
变式练习:1、在等腰中,∠A =50°, 则
∠B =___,∠C=___
2、在等腰中,∠A =100°, 则
∠B =___,∠C=___
C
B
A
C
B
A
C
B
A
(变式1①) (变式1② (变式1③)
(变式1①) (变式1②) (变式1③)
演示
B
C
D
A
某地地震后,同学们不确定教室的房梁是否水平,小强于是拿起一个等腰直角三角尺,在斜边中点栓一条线绳,线绳的另一端挂一个铅锤,把这个三角尺的斜边贴在房梁上,结果线绳经过三角尺的直角顶点,小强告诉同学们房梁是水平的 。小强说的对吗?道理是什么?
在数学的天地里,重要的不是我们知道什么,而是我们怎么知道什么。
——毕达哥拉斯
