北师大版 九年级 上册 4.6 利用相似三角形测高 练习 (Word版 含解析)
文档属性
| 名称 | 北师大版 九年级 上册 4.6 利用相似三角形测高 练习 (Word版 含解析) |  | |
| 格式 | docx | ||
| 文件大小 | 302.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-12-24 23:27:59 | ||
图片预览


文档简介
利用相似三角形测高练习
一、选择题
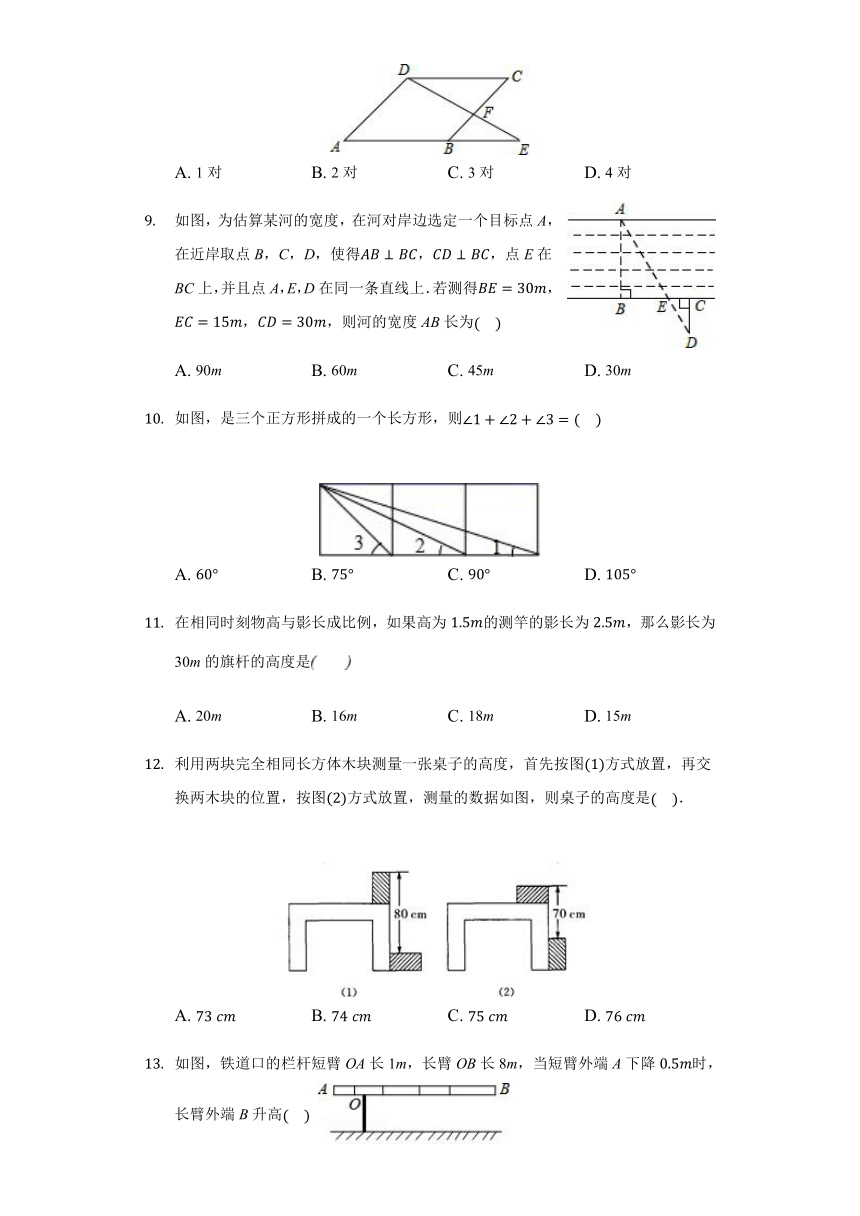
兴趣小组的同学要测量树的高度.在阳光下,一名同学测得一根长为1米的竹竿的影长为0.4米,同时另一名同学测量树的高度时,发现树的影子不全落在地面上,有一部分落在教学楼的第一级台阶上,测得该影子的长为0.2米,一级台阶高为0.3米,如图所示,若此时落在地面上的影长为4.4米,则树高为(????)
A. 11.5米 B. 11.75米 C. 11.8米 D. 12.25米
为了加强视力保护意识,小明要在书房里挂一张视力表.由于书房空间狭小,他想根据测试距离为5m的大视力表制作一个测试距离为3m的小视力表.如图,如果大视力表中“E”的高度是3.5cm,那么小视力表中相应“E”的高度是(????)
A. 3cm B. 2.5cm C. 2.3cm D. 2.1cm
如图,身高为1.6m的吴格霆想测量学校旗杆的高度,当她站在C处时,她头顶端的影子正好与旗杆顶端的影子重合,并测得AC=2.0m,BC=8.0m,则旗杆的高度是(????)
A. 6.4m B. 7.0m C. 8.0m D. 9.0m
三角尺在灯泡O的照射下在墙上形成的影子如图所示.若OA=20cm,OA′=50cm,则这个三角尺的周长与它在墙上形成的影子的周长的比是(????)
A. 5:2 B. 2:5 C. 4:25 D. 25:4
如图,方格纸中的△ABC经过变换得到△DEF,正确的变换是(????)
A. 把△ABC向右平移6格
B. 把△ABC向右平移4格,再向上平移1格
C. 把△ABC绕着点A顺时针方向旋转90?,再向右平移7格
D. 把△ABC绕着点A逆时针方向旋转90?,再向右平移7格
如图是小明设计用手电来测量某古城墙高度的示意图,点P处放一水平的平面镜,光线从点A出发经平面镜反射后刚好射到古城墙CD的顶端C处,已知AB⊥BD,CD⊥BD,且测得AB=1.2米,BP=1.8米,PD=12米,那么该古城墙的高度是(????)
A. 6米 B. 8米 C. 18米 D. 24米
如图是圆桌正上方的灯泡(看做一个点)发出的光线照射桌面后,在地面上形成阴影(圆形)的示意图,已知桌面的直径为1.2m,桌面距离地面1m.若灯泡距离地面3m,则地面上阴影部分的面积为(????)
A. 0.36π?m2 B. 0.81π?m2 C. 2π?m2 D. 3.24π?m2
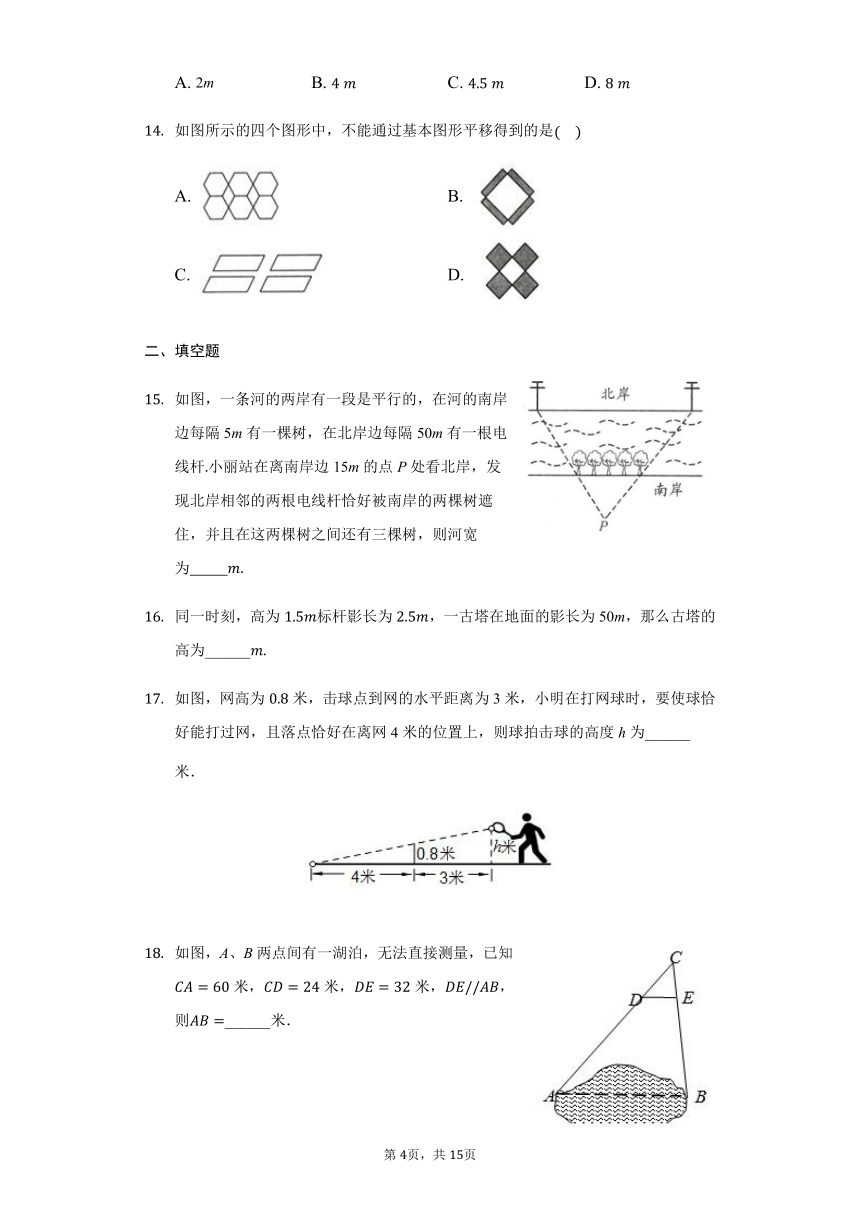
如图,E是?ABCD边AB的延长线上一点,DE交BC于F,则图中的相似三角形共有(????)
A. 1对 B. 2对 C. 3对 D. 4对
如图,为估算某河的宽度,在河对岸边选定一个目标点A,在近岸取点B,C,D,使得AB⊥BC,CD⊥BC,点E在BC上,并且点A,E,D在同一条直线上.若测得BE=30m,EC=15m,CD=30m,则河的宽度AB长为(????)
A. 90m B. 60m C. 45m D. 30m
如图,是三个正方形拼成的一个长方形,则∠1+∠2+∠3=(????)
A. 60° B. 75° C. 90° D. 105°
在相同时刻物高与影长成比例,如果高为1.5m的测竿的影长为2.5m,那么影长为30m的旗杆的高度是
A. 20m B. 16m C. 18m D. 15m
利用两块完全相同长方体木块测量一张桌子的高度,首先按图(1)方式放置,再交换两木块的位置,按图(2)方式放置,测量的数据如图,则桌子的高度是(????).
A. 73?cm B. 74?cm C. 75?cm D. 76?cm
如图,铁道口的栏杆短臂OA长1m,长臂OB长8m,当短臂外端A下降0.5m时,长臂外端B升高(????)
A. 2m B. 4?m C. 4.5?m D. 8?m
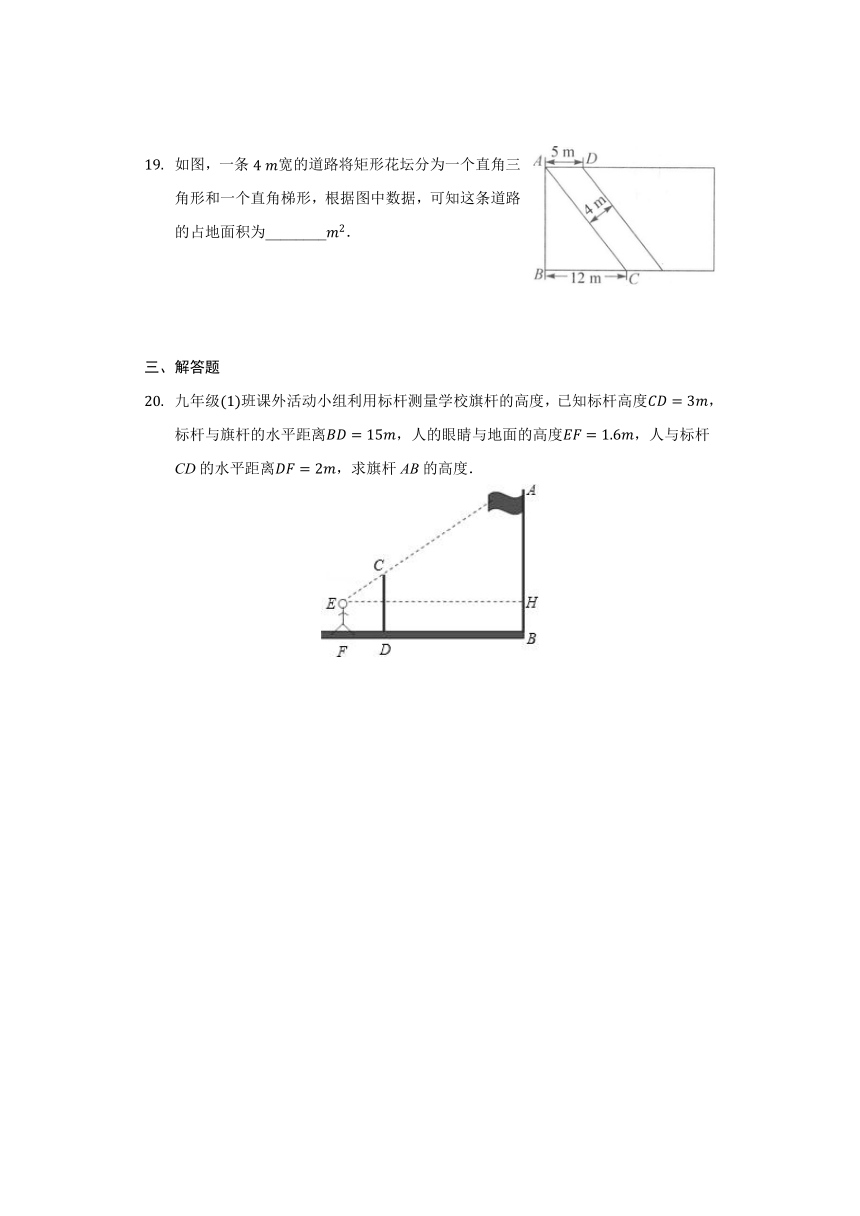
如图所示的四个图形中,不能通过基本图形平移得到的是(????)
A. B.
C. D.
二、填空题
如图,一条河的两岸有一段是平行的,在河的南岸边每隔5m有一棵树,在北岸边每隔50m有一根电线杆.小丽站在离南岸边15m的点P处看北岸,发现北岸相邻的两根电线杆恰好被南岸的两棵树遮住,并且在这两棵树之间还有三棵树,则河宽为??????????m.
同一时刻,高为1.5m标杆影长为2.5m,一古塔在地面的影长为50m,那么古塔的高为______m.
如图,网高为0.8米,击球点到网的水平距离为3米,小明在打网球时,要使球恰好能打过网,且落点恰好在离网4米的位置上,则球拍击球的高度h为______米.
如图,A、B两点间有一湖泊,无法直接测量,已知CA=60米,CD=24米,DE=32米,DE//AB,则AB=______米.
如图,一条4?m宽的道路将矩形花坛分为一个直角三角形和一个直角梯形,根据图中数据,可知这条道路的占地面积为________m2.
三、解答题
九年级(1)班课外活动小组利用标杆测量学校旗杆的高度,已知标杆高度CD=3m,标杆与旗杆的水平距离BD=15m,人的眼睛与地面的高度EF=1.6m,人与标杆CD的水平距离DF=2m,求旗杆AB的高度.
如图,在每个小正方形边长为1的方格纸中,三角形ABC的顶点都在方格纸格点上.将三角形ABC向左平移2格,再向上平移4格.
(1)请在图中画出平移后的三角形A′B′C′;
(2)再在图中画出三角形ABC的高CD;
(3)在图中能使S三角形PBC=?S三角形ABC的格点P有________个(点P异于A).
如图,△ABC是一块锐角三角形余料,边长BC=120cm,高AP=90cm,现在要把它加工成长方形零件DFHE,且满足FH=2DF,F、H在BC上,D、E分别在AB、AC上,求短边DF的长.
答案和解析
1.【答案】C
【解答】
解:如图,设AB为树高,BC为树在地面上的影子,CD和DE为树在台阶上的影子.
如果我们把BC平移到FD的位置,易知四边形FBCD是矩形,
因此FD=BC,则EF=FD+DE=4.6米.
设AB=x(x>0)米,则AF=(x?0.3)米.
根据题意,得10.4=x?0.34.6,解得x=11.8.
则树高为11.8米.
故选C.
2.【答案】D
【解析】解:由题意得:CD//AB,
∴CDAB=DEBE,
∵AB=3.5cm,BE=5m,DE=3m,
∴CD3.5=35,
∴CD=2.1cm,
3.【答案】C
【解析】解:设旗杆高度为h,
由题意得:1.6h=22+8,
解得:h=8.
4.【答案】B
【解析】解:如图,∵OA=20cm,OA′=50cm,
∴ABA′B′=OAOA′=2050=25,
∵三角尺与影子是相似三角形,
∴三角尺的周长与它在墙上形成的影子的周长的比=ABA′B′=2:5.
5.【答案】D
【解答】
解:由题图知△ABC绕着点A逆时针方向旋转90?,再向右平移7格就可以与△DEF重合.故D.
6.【答案】B
【解答】
解:由题意知:光线AP与光线PC,∠APB=∠CPD,
∴Rt△ABP∽Rt△CDP,
∴ABCD=BPPD,∴CD=1.2×121.8=8(米).
故选B.
7.【答案】B
【解析】解:构造几何模型如图:
依题意知DE=1.2米,FG=1米,AG=3米,
由△DAE∽△BAC得DEBC=AFAG,即1.2BC=3?13,
得BC=1.8,
故S圆=(12BC)2?π=(1.82)2?π=0.81π,
8.【答案】C
【解答】
解:图中相似三角形有:△BFE∽△ADE,△DFC∽△EFB,△DFC∽△EDA,共3对,
故选C.
9.【答案】B
【解答】
解:∵AB⊥BC,CD⊥BC,
∴∠ABE=∠DCE=90°,
又∵∠AEB=∠DEC(对顶角相等),
∴△ABE∽△DCE,
∴ABDC=BECE,
即AB30=3015,
解得AB=60m.
故选B.
10.【答案】C
【解答】
解:如图所示:
根据题意可知:∠3=45°,
设正方形的边长为1,则AD=DE2+EA2=2,
∴ABAD=12=22,ADAC=22.
∴ABAD=ADAC.
又∵∠DAB=∠CAD,
∴△DAB∽△CAD.
∴∠1=∠BDA.
∴∠1+∠2=∠2+∠BDA=∠3=45°.
∴∠1+∠2+∠3=45°+45°=90°.
故选:C.
11.【答案】C
【解答】
解:根据题意解:标杆的高标杆影长=旗杆的高旗杆的影长,
即1.52.5=旗杆高30,
∴旗杆的高=1.5×302.5=18m.
故选C.
12.【答案】C
【解答】
解:设桌子的高度为hcm,第一个长方体的长为xcm,第二个长方体的宽为ycm,
由第一个图形可知桌子的高度为:h?y+x=80,
由第二个图形可知桌子的高度为:h?x+y=70,
两个方程相加得:(h?y+x)+(h?x+y)=150,
解得:h=75cm.
故选C.
13.【答案】B
【解答】
解:如图所示,
?
由题意知OC=OA=1、OD=OB=8,
∵CE⊥AB、DF⊥AB,
∴CE//DF,
∴△OCE∽△ODF,
∴OCOD=CEDF,
即18=0.5DF,
解得:DF=4,
即长臂外端B升高4m,
故选:B.
14.【答案】B
【解答】
解:A、能通过其中一个正六边形平移得到,故此选项错误;?
B、不能通过其中一个长方形平移得到,故此选项符合题意;
C、能通过其中一个平行四边形平移得到,故此选项错误;
D、能通过其中一个正方形平移得到,故此选项错误.
故选B.
15.【答案】22.5
【解答】
解:如图,设河宽为hm.
因为AB//CD,所以ABCD=PEPF,
即2050=1515+h,解得h=22.5.
即河宽为22.5m.
16.【答案】30
【解析】解:设古塔的高度为xm,
∵标杆的高标杆影长=古塔的高古塔的影长,
即1.52.5=x50,解得,x=30.
17.【答案】1.4
【解答】
解:由题意得:44+3=0.8h,
解得h=1.4.
故答案为1.4.
18.【答案】80
【解答】
解:∵DE//AB,
∴∠CDE=∠CAB,∠CED=∠CBA
∴△CDE∽△CAB,
∴DEAB=CDCA,
∵CA=60米,CD=24米,DE=32米,
∴32AB=2460,
解得AB=80,
故答案为80.
19.【答案】80
【解答】
解:如图,作DE⊥AC于点E,
∵道路的宽为4m,
∴DE=4米,
∵AE=3m
∵∠DAE+∠BAE=90°,∠DAE+∠ADE=90°,
∴∠BAE=∠ADE
∴△DAE∽△ACB
∴DEAB=AEBC
即:4AB=312
解得:AB=16(m),
∴道路的面积为AD×AB=5×16=80(m2).
故答案为:80.
20.【答案】解:如图,设CD与EH交于点G,
∵CD⊥FB,AB⊥FB,
∴CD//AB
∴△CGE∽△AHE
∴CGAH=EGEH
即:CD?EFAH=FDFD+BD
∴3?1.6AH=22+15
∴AH=11.9
∴AB=AH+HB=AH+EF=11.9+1.6=13.5(m),
答:旗杆AB的高度为13.5m.
21.【答案】解:(1)△A′B′C′如图所示:
(2)△ABC的高CD如图所示:
;
(3)4.
故答案为4.?
22.【答案】解:设DF=xcm,
则DE=2xcm,AK=(90?x)cm,
∵DE//BC,
∴△ADE∽△ABC,
∴AKAP=DEBC,
∴90?x90=2x120,
∴x=36,
∴DF的长为36cm.
一、选择题
兴趣小组的同学要测量树的高度.在阳光下,一名同学测得一根长为1米的竹竿的影长为0.4米,同时另一名同学测量树的高度时,发现树的影子不全落在地面上,有一部分落在教学楼的第一级台阶上,测得该影子的长为0.2米,一级台阶高为0.3米,如图所示,若此时落在地面上的影长为4.4米,则树高为(????)
A. 11.5米 B. 11.75米 C. 11.8米 D. 12.25米
为了加强视力保护意识,小明要在书房里挂一张视力表.由于书房空间狭小,他想根据测试距离为5m的大视力表制作一个测试距离为3m的小视力表.如图,如果大视力表中“E”的高度是3.5cm,那么小视力表中相应“E”的高度是(????)
A. 3cm B. 2.5cm C. 2.3cm D. 2.1cm
如图,身高为1.6m的吴格霆想测量学校旗杆的高度,当她站在C处时,她头顶端的影子正好与旗杆顶端的影子重合,并测得AC=2.0m,BC=8.0m,则旗杆的高度是(????)
A. 6.4m B. 7.0m C. 8.0m D. 9.0m
三角尺在灯泡O的照射下在墙上形成的影子如图所示.若OA=20cm,OA′=50cm,则这个三角尺的周长与它在墙上形成的影子的周长的比是(????)
A. 5:2 B. 2:5 C. 4:25 D. 25:4
如图,方格纸中的△ABC经过变换得到△DEF,正确的变换是(????)
A. 把△ABC向右平移6格
B. 把△ABC向右平移4格,再向上平移1格
C. 把△ABC绕着点A顺时针方向旋转90?,再向右平移7格
D. 把△ABC绕着点A逆时针方向旋转90?,再向右平移7格
如图是小明设计用手电来测量某古城墙高度的示意图,点P处放一水平的平面镜,光线从点A出发经平面镜反射后刚好射到古城墙CD的顶端C处,已知AB⊥BD,CD⊥BD,且测得AB=1.2米,BP=1.8米,PD=12米,那么该古城墙的高度是(????)
A. 6米 B. 8米 C. 18米 D. 24米
如图是圆桌正上方的灯泡(看做一个点)发出的光线照射桌面后,在地面上形成阴影(圆形)的示意图,已知桌面的直径为1.2m,桌面距离地面1m.若灯泡距离地面3m,则地面上阴影部分的面积为(????)
A. 0.36π?m2 B. 0.81π?m2 C. 2π?m2 D. 3.24π?m2
如图,E是?ABCD边AB的延长线上一点,DE交BC于F,则图中的相似三角形共有(????)
A. 1对 B. 2对 C. 3对 D. 4对
如图,为估算某河的宽度,在河对岸边选定一个目标点A,在近岸取点B,C,D,使得AB⊥BC,CD⊥BC,点E在BC上,并且点A,E,D在同一条直线上.若测得BE=30m,EC=15m,CD=30m,则河的宽度AB长为(????)
A. 90m B. 60m C. 45m D. 30m
如图,是三个正方形拼成的一个长方形,则∠1+∠2+∠3=(????)
A. 60° B. 75° C. 90° D. 105°
在相同时刻物高与影长成比例,如果高为1.5m的测竿的影长为2.5m,那么影长为30m的旗杆的高度是
A. 20m B. 16m C. 18m D. 15m
利用两块完全相同长方体木块测量一张桌子的高度,首先按图(1)方式放置,再交换两木块的位置,按图(2)方式放置,测量的数据如图,则桌子的高度是(????).
A. 73?cm B. 74?cm C. 75?cm D. 76?cm
如图,铁道口的栏杆短臂OA长1m,长臂OB长8m,当短臂外端A下降0.5m时,长臂外端B升高(????)
A. 2m B. 4?m C. 4.5?m D. 8?m
如图所示的四个图形中,不能通过基本图形平移得到的是(????)
A. B.
C. D.
二、填空题
如图,一条河的两岸有一段是平行的,在河的南岸边每隔5m有一棵树,在北岸边每隔50m有一根电线杆.小丽站在离南岸边15m的点P处看北岸,发现北岸相邻的两根电线杆恰好被南岸的两棵树遮住,并且在这两棵树之间还有三棵树,则河宽为??????????m.
同一时刻,高为1.5m标杆影长为2.5m,一古塔在地面的影长为50m,那么古塔的高为______m.
如图,网高为0.8米,击球点到网的水平距离为3米,小明在打网球时,要使球恰好能打过网,且落点恰好在离网4米的位置上,则球拍击球的高度h为______米.
如图,A、B两点间有一湖泊,无法直接测量,已知CA=60米,CD=24米,DE=32米,DE//AB,则AB=______米.
如图,一条4?m宽的道路将矩形花坛分为一个直角三角形和一个直角梯形,根据图中数据,可知这条道路的占地面积为________m2.
三、解答题
九年级(1)班课外活动小组利用标杆测量学校旗杆的高度,已知标杆高度CD=3m,标杆与旗杆的水平距离BD=15m,人的眼睛与地面的高度EF=1.6m,人与标杆CD的水平距离DF=2m,求旗杆AB的高度.
如图,在每个小正方形边长为1的方格纸中,三角形ABC的顶点都在方格纸格点上.将三角形ABC向左平移2格,再向上平移4格.
(1)请在图中画出平移后的三角形A′B′C′;
(2)再在图中画出三角形ABC的高CD;
(3)在图中能使S三角形PBC=?S三角形ABC的格点P有________个(点P异于A).
如图,△ABC是一块锐角三角形余料,边长BC=120cm,高AP=90cm,现在要把它加工成长方形零件DFHE,且满足FH=2DF,F、H在BC上,D、E分别在AB、AC上,求短边DF的长.
答案和解析
1.【答案】C
【解答】
解:如图,设AB为树高,BC为树在地面上的影子,CD和DE为树在台阶上的影子.
如果我们把BC平移到FD的位置,易知四边形FBCD是矩形,
因此FD=BC,则EF=FD+DE=4.6米.
设AB=x(x>0)米,则AF=(x?0.3)米.
根据题意,得10.4=x?0.34.6,解得x=11.8.
则树高为11.8米.
故选C.
2.【答案】D
【解析】解:由题意得:CD//AB,
∴CDAB=DEBE,
∵AB=3.5cm,BE=5m,DE=3m,
∴CD3.5=35,
∴CD=2.1cm,
3.【答案】C
【解析】解:设旗杆高度为h,
由题意得:1.6h=22+8,
解得:h=8.
4.【答案】B
【解析】解:如图,∵OA=20cm,OA′=50cm,
∴ABA′B′=OAOA′=2050=25,
∵三角尺与影子是相似三角形,
∴三角尺的周长与它在墙上形成的影子的周长的比=ABA′B′=2:5.
5.【答案】D
【解答】
解:由题图知△ABC绕着点A逆时针方向旋转90?,再向右平移7格就可以与△DEF重合.故D.
6.【答案】B
【解答】
解:由题意知:光线AP与光线PC,∠APB=∠CPD,
∴Rt△ABP∽Rt△CDP,
∴ABCD=BPPD,∴CD=1.2×121.8=8(米).
故选B.
7.【答案】B
【解析】解:构造几何模型如图:
依题意知DE=1.2米,FG=1米,AG=3米,
由△DAE∽△BAC得DEBC=AFAG,即1.2BC=3?13,
得BC=1.8,
故S圆=(12BC)2?π=(1.82)2?π=0.81π,
8.【答案】C
【解答】
解:图中相似三角形有:△BFE∽△ADE,△DFC∽△EFB,△DFC∽△EDA,共3对,
故选C.
9.【答案】B
【解答】
解:∵AB⊥BC,CD⊥BC,
∴∠ABE=∠DCE=90°,
又∵∠AEB=∠DEC(对顶角相等),
∴△ABE∽△DCE,
∴ABDC=BECE,
即AB30=3015,
解得AB=60m.
故选B.
10.【答案】C
【解答】
解:如图所示:
根据题意可知:∠3=45°,
设正方形的边长为1,则AD=DE2+EA2=2,
∴ABAD=12=22,ADAC=22.
∴ABAD=ADAC.
又∵∠DAB=∠CAD,
∴△DAB∽△CAD.
∴∠1=∠BDA.
∴∠1+∠2=∠2+∠BDA=∠3=45°.
∴∠1+∠2+∠3=45°+45°=90°.
故选:C.
11.【答案】C
【解答】
解:根据题意解:标杆的高标杆影长=旗杆的高旗杆的影长,
即1.52.5=旗杆高30,
∴旗杆的高=1.5×302.5=18m.
故选C.
12.【答案】C
【解答】
解:设桌子的高度为hcm,第一个长方体的长为xcm,第二个长方体的宽为ycm,
由第一个图形可知桌子的高度为:h?y+x=80,
由第二个图形可知桌子的高度为:h?x+y=70,
两个方程相加得:(h?y+x)+(h?x+y)=150,
解得:h=75cm.
故选C.
13.【答案】B
【解答】
解:如图所示,
?
由题意知OC=OA=1、OD=OB=8,
∵CE⊥AB、DF⊥AB,
∴CE//DF,
∴△OCE∽△ODF,
∴OCOD=CEDF,
即18=0.5DF,
解得:DF=4,
即长臂外端B升高4m,
故选:B.
14.【答案】B
【解答】
解:A、能通过其中一个正六边形平移得到,故此选项错误;?
B、不能通过其中一个长方形平移得到,故此选项符合题意;
C、能通过其中一个平行四边形平移得到,故此选项错误;
D、能通过其中一个正方形平移得到,故此选项错误.
故选B.
15.【答案】22.5
【解答】
解:如图,设河宽为hm.
因为AB//CD,所以ABCD=PEPF,
即2050=1515+h,解得h=22.5.
即河宽为22.5m.
16.【答案】30
【解析】解:设古塔的高度为xm,
∵标杆的高标杆影长=古塔的高古塔的影长,
即1.52.5=x50,解得,x=30.
17.【答案】1.4
【解答】
解:由题意得:44+3=0.8h,
解得h=1.4.
故答案为1.4.
18.【答案】80
【解答】
解:∵DE//AB,
∴∠CDE=∠CAB,∠CED=∠CBA
∴△CDE∽△CAB,
∴DEAB=CDCA,
∵CA=60米,CD=24米,DE=32米,
∴32AB=2460,
解得AB=80,
故答案为80.
19.【答案】80
【解答】
解:如图,作DE⊥AC于点E,
∵道路的宽为4m,
∴DE=4米,
∵AE=3m
∵∠DAE+∠BAE=90°,∠DAE+∠ADE=90°,
∴∠BAE=∠ADE
∴△DAE∽△ACB
∴DEAB=AEBC
即:4AB=312
解得:AB=16(m),
∴道路的面积为AD×AB=5×16=80(m2).
故答案为:80.
20.【答案】解:如图,设CD与EH交于点G,
∵CD⊥FB,AB⊥FB,
∴CD//AB
∴△CGE∽△AHE
∴CGAH=EGEH
即:CD?EFAH=FDFD+BD
∴3?1.6AH=22+15
∴AH=11.9
∴AB=AH+HB=AH+EF=11.9+1.6=13.5(m),
答:旗杆AB的高度为13.5m.
21.【答案】解:(1)△A′B′C′如图所示:
(2)△ABC的高CD如图所示:
;
(3)4.
故答案为4.?
22.【答案】解:设DF=xcm,
则DE=2xcm,AK=(90?x)cm,
∵DE//BC,
∴△ADE∽△ABC,
∴AKAP=DEBC,
∴90?x90=2x120,
∴x=36,
∴DF的长为36cm.
同课章节目录
- 第一章 特殊平行四边形
- 1 菱形的性质与判定
- 2 矩形的性质与判定
- 3 正方形的性质与判定
- 第二章 一元二次方程
- 1 认识一元二次方程
- 2 用配方法求解一元二次方程
- 3 用公式法求解一元二次方程
- 4 用因式分解法求解一元二次方程
- 5 一元二次方程的根与系数的关系
- 6 应用一元二次方程
- 第三章 概率的进一步认识
- 1 用树状图或表格求概率
- 2 用频率估计概率
- 第四章 图形的相似
- 1 成比例线段
- 2 平行线分线段成比例
- 3 相似多边形
- 4 探索三角形相似的条件
- 5 相似三角形判定定理的证明
- 6 利用相似三角形测高
- 7 相似三角形的性质
- 8 图形的位似
- 第五章 投影与视图
- 1 投影
- 2 视图
- 第六章 反比例函数
- 1 反比例函数
- 2 反比例函数的图象与性质
- 3 反比例函数的应用
