北师大版 九年级 上册 4.4 探索三角形相似的条件 练习 (Word版 含解析)
文档属性
| 名称 | 北师大版 九年级 上册 4.4 探索三角形相似的条件 练习 (Word版 含解析) |
|
|
| 格式 | docx | ||
| 文件大小 | 154.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-12-24 00:00:00 | ||
图片预览


文档简介
探索三角形相似的条件练习
一、选择题
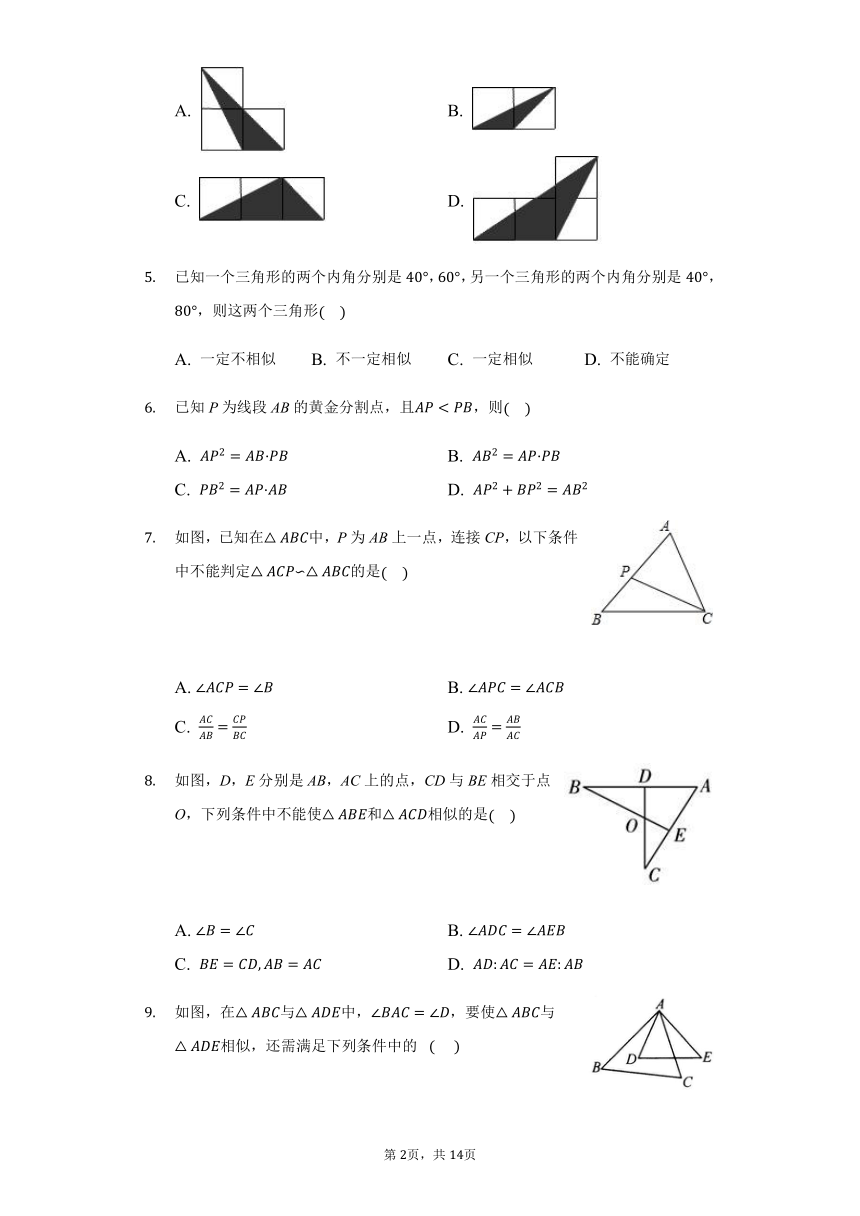
如图,在平面直角坐标系中,A(0,4),B(2,0),点C在第一象限,若以A,B,C为顶点的三角形与时△AOB相似(不包括全等),则点C的个数是(? ? ? )
A. 1 B. 2 C. 3 D. 4
如图,在△ABC中,∠A=78°,AB=4,AC=6,将△ABC沿图示中的虚线剪开,剪下的阴影三角形与原三角形不相似的是(????)
A. B.
C. D.
下列两个三角形不相似的是(????)
A. 一个三角形的两个角分别是40°、80°;另一个三角形的两上角分别是60°、80°
B. 一个三角形的三边长分别是4cm、6cm、8cm;另一个三角形的三边长分别是12cm、18cm、21cm
C. 一个三角形的两边长分别是2cm和5cm,夹角是40°;另一个三角形的两边长分别是3cm和7.5cm,夹角是40°
D. 各有一个角是120°的两个等腰三角形
如图,小正方形的边长均为1,则下列图中的三角形(阴影部分)与△ABC相似的是(????)
A. B.
C. D.
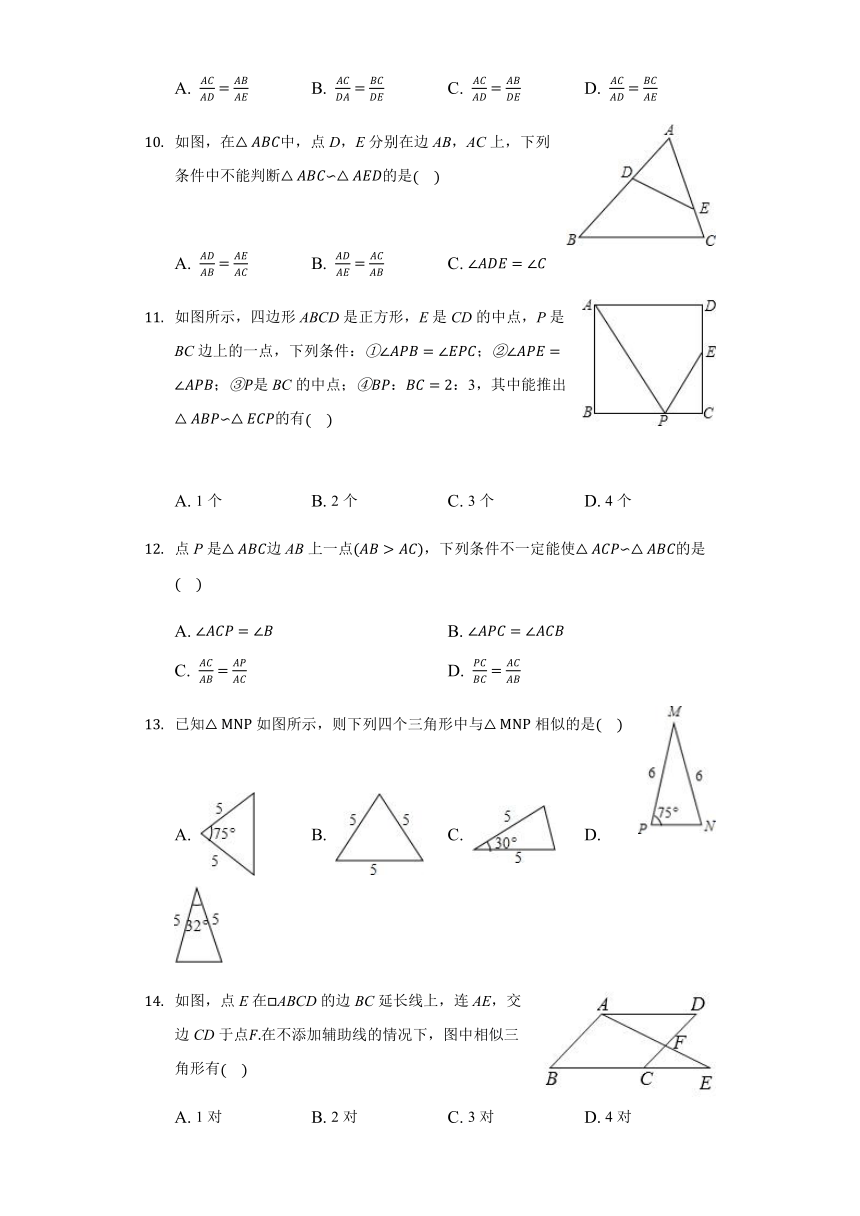
已知一个三角形的两个内角分别是40°,60°,另一个三角形的两个内角分别是40°,80°,则这两个三角形(????)
A. 一定不相似 B. 不一定相似 C. 一定相似 D. 不能确定
已知P为线段AB的黄金分割点,且AP A. AP2=AB·PB B. AB2=AP·PB
C. PB2=AP·AB D. AP2+BP2=AB2
如图,已知在△ABC中,P为AB上一点,连接CP,以下条件中不能判定△ACP∽△ABC的是(????)
A. ∠ACP=∠B B. ∠APC=∠ACB
C. ACAB=CPBC D. ACAP=ABAC
如图,D,E分别是AB,AC上的点,CD与BE相交于点O,下列条件中不能使△ABE和△ACD相似的是(????)
A. ∠B=∠C B. ∠ADC=∠AEB
C. BE=CD,AB=AC D. AD:AC=AE:AB
如图,在△ABC与△ADE中,∠BAC=∠D,要使△ABC与△ADE相似,还需满足下列条件中的? (??? )
A. ACAD=ABAE B. ACDA=BCDE C. ACAD=ABDE D. ACAD=BCAE
如图,在△ABC中,点D,E分别在边AB,AC上,下列条件中不能判断△ABC∽△AED的是(????)
A. ADAB=AEAC B. ADAE=ACAB C. ∠ADE=∠C D. ∠AED=∠B
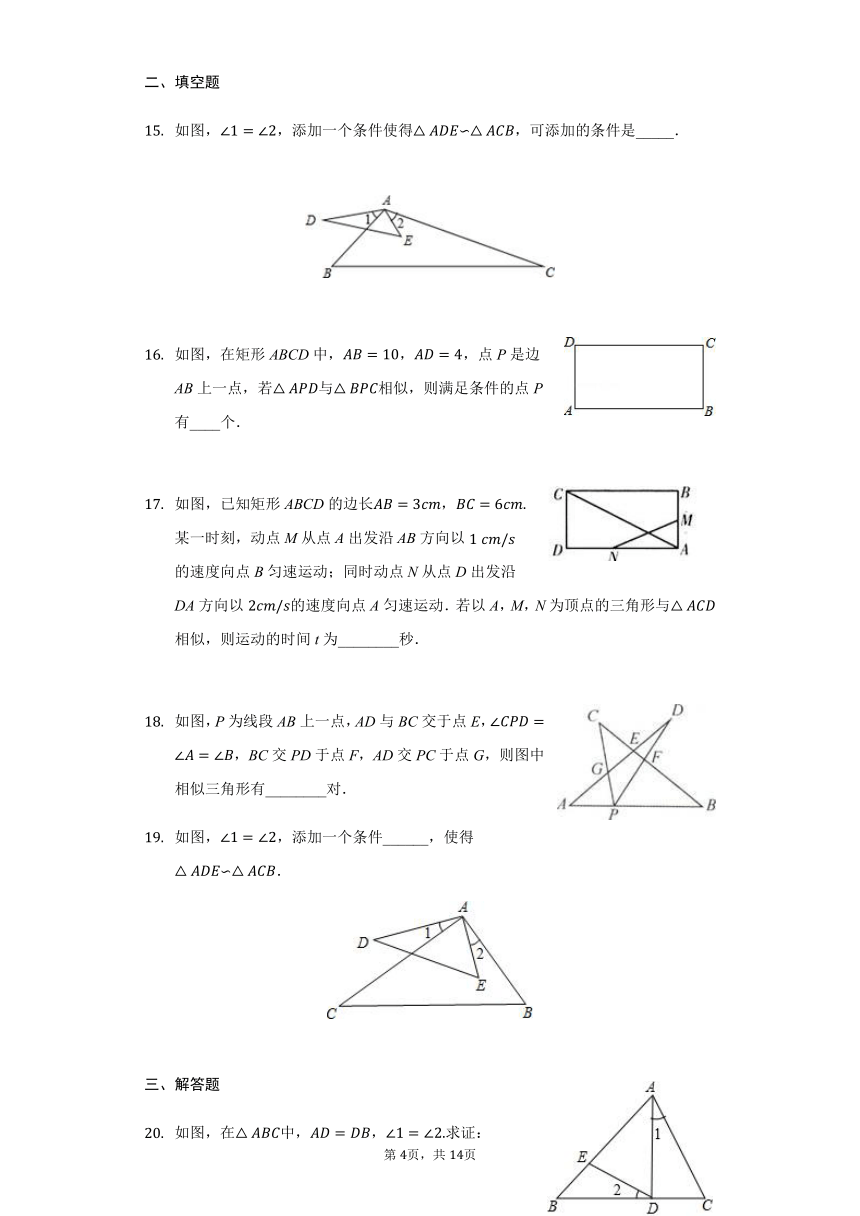
如图所示,四边形ABCD是正方形,E是CD的中点,P是BC边上的一点,下列条件:①∠APB=∠EPC;②∠APE=∠APB;③P是BC的中点;④BP:BC=2:3,其中能推出△ABP∽△ECP的有(????)
A. 1个 B. 2个 C. 3个 D. 4个
点P是△ABC边AB上一点(AB>AC),下列条件不一定能使△ACP∽△ABC的是(????)
A. ∠ACP=∠B B. ∠APC=∠ACB
C. ACAB=APAC D. PCBC=ACAB
已知△MNP如图所示,则下列四个三角形中与△MNP相似的是(????)
A. B. C. D.
如图,点E在□ABCD的边BC延长线上,连AE,交边CD于点F.在不添加辅助线的情况下,图中相似三角形有(????)
A. 1对 B. 2对 C. 3对 D. 4对
二、填空题
如图,∠1=∠2,添加一个条件使得△ADE∽△ACB,可添加的条件是_____.
如图,在矩形ABCD中,AB=10,AD=4,点P是边AB上一点,若△APD与△BPC相似,则满足条件的点P有____个.
如图,已知矩形ABCD的边长AB=3cm,BC=6cm.某一时刻,动点M从点A出发沿AB方向以1?cm/s的速度向点B匀速运动;同时动点N从点D出发沿DA方向以2cm/s的速度向点A匀速运动.若以A,M,N为顶点的三角形与△ACD相似,则运动的时间t为________秒.
如图,P为线段AB上一点,AD与BC交于点E,∠CPD=∠A=∠B,BC交PD于点F,AD交PC于点G,则图中相似三角形有________对.
如图,∠1=∠2,添加一个条件______,使得△ADE∽△ACB.
三、解答题
如图,在△ABC中,AD=DB,∠1=∠2.求证:△ABC∽△EAD.
如图,在△ABC中,AB=8cm,BC=16cm,点P从点A开始沿边AB向点B以2cm/s的速度移动,点Q从点B开始沿边BC向点C以4cm/s的速度移动,如果点P、Q分别从点A、B同时出发,经几秒钟△PBQ与△ABC相似?试说明理由.
已知:如图,在正方形ABCD中,P是BC上的点,且BP=3PC,Q是CD的中点.
求证:△ADQ∽△QCP.
答案和解析
1.【答案】D
【解答】
解:如图①,∠OAB=∠BAC1,∠AOB=∠ABC1时,△AOB∽△ABC1.
如图②,AO//BC2,BA⊥AC2,则∠ABC2=∠OAB,∠AOB=∠BAC2?,故△AOB∽△BAC2;
如图③,AC3//OB,∠ABC3=90°,则∠ABO=∠C3AB,∠ABC3=∠AOB=90°?,故△AOB∽△C3BA;
如图④,∠AOB=∠BAC4=90°,∠ABO=∠ABC4,则△AOB∽△C4AB.
故选D.
2.【答案】C
【解答】
解:A、阴影部分的三角形与原三角形有两个角相等,故两三角形相似,故本选项错误;
B、阴影部分的三角形与原三角形有两个角相等,故两三角形相似,故本选项错误;
C、两三角形的对应边不成比例,故两三角形不相似,故本选项正确.
D、两三角形对应边成比例且夹角相等,故两三角形相似,故本选项错误;
故选:C.
3.【答案】B
解:A、一个三角形的两个角分别是40°、80°,则另一个内角为60°,而另一个三角形的两上角分别是60°、80°,这两个三角形相似;
B、一个三角形的三边长分别是4cm、6cm、8cm;另一个三角形的三边长分别是12cm、18cm、21cm,三边不成比例,这两个三角形不相似;
C、根据两边对应成比例且夹角相等知这两个三角形相似;
D、各有一个角是120°的两个等腰三角形,由于两个等腰三角形的底角均为30°,据此可知两个三角形相似;
故选:B.
4.【答案】B
【解答】
解:由正方形的性质可知,∠ACB=180°?45°=135°,
A、C、D图形中的钝角都不等于135°,
由勾股定理得,BC=2,AC=2,
对应的图形B中的边长分别为1和2,
∵12=22,
∴图B中的三角形(阴影部分)与△ABC相似,
故选B.
5.【答案】C
【解析】解:∵一个三角形的两个内角分别是40°,60°,
∴第三个内角为80°,
又∵另一个三角形的两个内角分别是40°,80°,
∴这两个三角形有两个内角相等,
∴这两个三角形相似.
6.【答案】C
较长的线段为全线段与较短线段的比例中项,这样的线段分割叫做黄金分割,他们的比值(
5?1
2
)叫做黄金比.
【解答】
解:∵P为线段AB的黄金分割点,且AP∴PB2=AP?AB.
故选C.
7.【答案】C
【解答】
解:A、∵∠A=∠A,∠ACP=∠B,
∴△ACP∽△ABC,
所以此选项的条件可以判定△ACP∽△ABC;
B、∵∠A=∠A,∠APC=∠ACB,
∴△ACP∽△ABC,
所以此选项的条件可以判定△ACP∽△ABC;
C、∵ACAB=CPBC,
当∠ACP=∠B时,△ACP∽△ABC,
所以此选项的条件不能判定△ACP∽△ABC;
D、∵ACAP=ABAC,
又∠A=∠A,
∴△ACP∽△ABC,
8.【答案】C
【解答】
解:∵∠A=∠A,
∴A.当∠B=∠C时,△ABE∽△ACD(两个对应角相等的两个三角形相似);
B.当∠ADC=∠AEB,△ABE∽△ACD(两个对应角相等的两个三角形相似);
C.当BE=CD,AB=AC时,无法证明△ABE和△ACD相似;
D.当AD:AC=AE:AB时,△ABE和△ACD相似(两组对应边成比例,且夹角相等的两个三角形相似).
故选C.
9.【答案】C
【解答】
解:∵∠BAC=∠D,ACAD=ABDE,
∴△ABC∽△DEA.
故选C.
10.【答案】A
【解答】
解:∵∠DAE=∠CAB,
∴当∠AED=∠B或∠ADE=∠C时,△ABC∽△AED;
当ADAC=AEAB即ADAE=ACAB时,△ABC∽△AED.
故选A.
11.【答案】B
利用相似三角形的判定定理,以及正方形的性质逐项判断即可.
【解答】
解:∵四边形ABCD为正方形,
∴AB=BC=CD,∠B=∠C=90°,
∵E为CD中点,
∴CD=2CE,即AB=BC=2CE,
①当∠APB=∠EPC时,结合∠B=∠C,可推出△ABP∽△ECP;
②当∠APE=∠APB≠60°时,则有∠APB≠∠EPC,所以不能推出△ABP∽△ECP;
③当P是BC中点时,则有BC=2PC,可知PC=CE,则△PCE为等腰直角三角形,而BP≠AB,即△ABP不是等腰直角三角形,故不能推出△ABP∽△ECP;
④当BP:BC=2:3时,则有BP:PC=2:1,且AB:CE=2:1,结合∠B=∠C,可推出△ABP∽△ECP.
故选B.
12.【答案】D
【解析】解:∵∠A=∠A,
∴当∠APC=∠ACB或∠ACP=∠B或AC:AB=AP:AC时,
△ACP∽△ABC.
13.【答案】C
【解答】
解:根据题意可知
选项A,三角形的顶角是75°,原?三角形的顶角是30°,对应角不相等,两个三角形不相似,故错误;
选项B,三角形是等边三角形,原三角形是顶角为30°的三角形,故不相似;故错误;
选项C,三角形是顶角为30°的等腰三角形,根据两边对应成比例,且夹角相等的两个三角形相似,便可以得到两个三角形相似,故正确;
选项D,三角形是顶角为32°的等腰三角形,原三角形的顶角是30°,与原三角形不相似,故错误.
故选C.
14.【答案】C
【解答】
解:∵四边形ABCD是平行四边形,
∴AD//BC,AB//CD,
∴△AFD∽△EFC∽△EAB.
故选C.
15.【答案】∠D=∠C或∠E=∠B或AEAB=ADAC
【解答】
解:∵∠1=∠2,
∴∠1+∠BAE=∠2+∠BAE,即∠DAE=∠CAB.
当∠D=∠C或∠E=∠B或AEAB=ADAC时,△ADE∽△ACB.
故答案为∠D=∠C或∠E=∠B或AEAB=ADAC.
16.【答案】3
【解答】
解:如图,
设AP为x,
∵AB=10,
∴PB=10?x,
①AD和PB是对应边时,
∵△APD与△BPC相似,
∴ADPB=APBC,
即410?x=x4,
整理得,x2?10x+16=0,
解得x1=2,x2=8,
②AD和BC是对应边时,
∵△APD与△BPC相似,
∴ADBC=APPB,
即44=x10?x,
解得x=5,
所以,当AP=2、5、8时,△APD与△BPC相似,
满足条件的点P有3个.
故答案为3.
17.【答案】2.4或1.5
∽△NMA两种情况进行讨论,再根据相似三角形的对应边成比例求解即可.
【解答】
解:当△ACD∽△MNA时,
则ADCD=MANA,
即63=t6?2t,
∴36?12t=3t.
∴t=2.4秒.
当△ACD∽△NMA时,
则ADCD=NAMA,
即63=6?2tt.
∴6t=18?6t.
∴t=1.5秒.
故答案为2.4或1.5.
18.【答案】3
【解答】
解:∵∠CPD=∠B,∠C=∠C,
∴△PCF∽△BCP.
∵∠CPD=∠A,∠D=∠D,
∴△APD∽△PGD.
∵∠CPD=∠A=∠B,∠APG=∠B+∠C,∠BFP=∠CPD+∠C,
∴∠APG=∠BFP,
∴△APG∽△BFP,
∴题图中有3对相似三角形.
故答案为3.
19.【答案】∠D=∠C或∠E=∠B或ADAC=AEAB
【解析】解:∵∠1=∠2,∴∠1+∠BAE=∠2+∠BAE,即∠DAE=∠CAB.
当∠D=∠C或∠E=∠B或ADAC=AEAB时,△ADE∽△ACB.
由∠1=∠2可得∠DAE=∠CAB.只需还有一对角对应相等或夹边对应成比例即可使得△ADE∽△ACB.
20.【答案】证明:∵AD=DB,
∴∠B=∠BAD.
∵∠BDA=∠1+∠C=∠2+∠ADE,
又∵∠1=∠2,
∴∠C=∠ADE.
∴△ABC∽△EAD.
21.【答案】解:设经x秒钟△PBQ与△ABC相似,
则AP=2xcm,BQ=4xcm,
∵AB=8cm,BC=16cm,
∴BP=AB?AP=(8?2x)cm,
∵∠B是公共角,
∵①当BPBA=BQBC,即8?2x8=4x16时,△PBQ∽△ABC,
解得:x=2;
②当BPBC=BQBA,即8?2x16=4x8时,△QBP∽△ABC,
解得:x=0.8,
∴经2或0.8秒钟△PBQ与△ABC相似.
22.【答案】证明:∵四边形ABCD是正方形,BP=3PC,Q是CD的中点,
∴QC=QD=12AD,CP=14AD,
∴ADQC=DQCP,
又∵∠ADQ=∠QCP,
∴△ADQ∽△QCP.
一、选择题
如图,在平面直角坐标系中,A(0,4),B(2,0),点C在第一象限,若以A,B,C为顶点的三角形与时△AOB相似(不包括全等),则点C的个数是(? ? ? )
A. 1 B. 2 C. 3 D. 4
如图,在△ABC中,∠A=78°,AB=4,AC=6,将△ABC沿图示中的虚线剪开,剪下的阴影三角形与原三角形不相似的是(????)
A. B.
C. D.
下列两个三角形不相似的是(????)
A. 一个三角形的两个角分别是40°、80°;另一个三角形的两上角分别是60°、80°
B. 一个三角形的三边长分别是4cm、6cm、8cm;另一个三角形的三边长分别是12cm、18cm、21cm
C. 一个三角形的两边长分别是2cm和5cm,夹角是40°;另一个三角形的两边长分别是3cm和7.5cm,夹角是40°
D. 各有一个角是120°的两个等腰三角形
如图,小正方形的边长均为1,则下列图中的三角形(阴影部分)与△ABC相似的是(????)
A. B.
C. D.
已知一个三角形的两个内角分别是40°,60°,另一个三角形的两个内角分别是40°,80°,则这两个三角形(????)
A. 一定不相似 B. 不一定相似 C. 一定相似 D. 不能确定
已知P为线段AB的黄金分割点,且AP
C. PB2=AP·AB D. AP2+BP2=AB2
如图,已知在△ABC中,P为AB上一点,连接CP,以下条件中不能判定△ACP∽△ABC的是(????)
A. ∠ACP=∠B B. ∠APC=∠ACB
C. ACAB=CPBC D. ACAP=ABAC
如图,D,E分别是AB,AC上的点,CD与BE相交于点O,下列条件中不能使△ABE和△ACD相似的是(????)
A. ∠B=∠C B. ∠ADC=∠AEB
C. BE=CD,AB=AC D. AD:AC=AE:AB
如图,在△ABC与△ADE中,∠BAC=∠D,要使△ABC与△ADE相似,还需满足下列条件中的? (??? )
A. ACAD=ABAE B. ACDA=BCDE C. ACAD=ABDE D. ACAD=BCAE
如图,在△ABC中,点D,E分别在边AB,AC上,下列条件中不能判断△ABC∽△AED的是(????)
A. ADAB=AEAC B. ADAE=ACAB C. ∠ADE=∠C D. ∠AED=∠B
如图所示,四边形ABCD是正方形,E是CD的中点,P是BC边上的一点,下列条件:①∠APB=∠EPC;②∠APE=∠APB;③P是BC的中点;④BP:BC=2:3,其中能推出△ABP∽△ECP的有(????)
A. 1个 B. 2个 C. 3个 D. 4个
点P是△ABC边AB上一点(AB>AC),下列条件不一定能使△ACP∽△ABC的是(????)
A. ∠ACP=∠B B. ∠APC=∠ACB
C. ACAB=APAC D. PCBC=ACAB
已知△MNP如图所示,则下列四个三角形中与△MNP相似的是(????)
A. B. C. D.
如图,点E在□ABCD的边BC延长线上,连AE,交边CD于点F.在不添加辅助线的情况下,图中相似三角形有(????)
A. 1对 B. 2对 C. 3对 D. 4对
二、填空题
如图,∠1=∠2,添加一个条件使得△ADE∽△ACB,可添加的条件是_____.
如图,在矩形ABCD中,AB=10,AD=4,点P是边AB上一点,若△APD与△BPC相似,则满足条件的点P有____个.
如图,已知矩形ABCD的边长AB=3cm,BC=6cm.某一时刻,动点M从点A出发沿AB方向以1?cm/s的速度向点B匀速运动;同时动点N从点D出发沿DA方向以2cm/s的速度向点A匀速运动.若以A,M,N为顶点的三角形与△ACD相似,则运动的时间t为________秒.
如图,P为线段AB上一点,AD与BC交于点E,∠CPD=∠A=∠B,BC交PD于点F,AD交PC于点G,则图中相似三角形有________对.
如图,∠1=∠2,添加一个条件______,使得△ADE∽△ACB.
三、解答题
如图,在△ABC中,AD=DB,∠1=∠2.求证:△ABC∽△EAD.
如图,在△ABC中,AB=8cm,BC=16cm,点P从点A开始沿边AB向点B以2cm/s的速度移动,点Q从点B开始沿边BC向点C以4cm/s的速度移动,如果点P、Q分别从点A、B同时出发,经几秒钟△PBQ与△ABC相似?试说明理由.
已知:如图,在正方形ABCD中,P是BC上的点,且BP=3PC,Q是CD的中点.
求证:△ADQ∽△QCP.
答案和解析
1.【答案】D
【解答】
解:如图①,∠OAB=∠BAC1,∠AOB=∠ABC1时,△AOB∽△ABC1.
如图②,AO//BC2,BA⊥AC2,则∠ABC2=∠OAB,∠AOB=∠BAC2?,故△AOB∽△BAC2;
如图③,AC3//OB,∠ABC3=90°,则∠ABO=∠C3AB,∠ABC3=∠AOB=90°?,故△AOB∽△C3BA;
如图④,∠AOB=∠BAC4=90°,∠ABO=∠ABC4,则△AOB∽△C4AB.
故选D.
2.【答案】C
【解答】
解:A、阴影部分的三角形与原三角形有两个角相等,故两三角形相似,故本选项错误;
B、阴影部分的三角形与原三角形有两个角相等,故两三角形相似,故本选项错误;
C、两三角形的对应边不成比例,故两三角形不相似,故本选项正确.
D、两三角形对应边成比例且夹角相等,故两三角形相似,故本选项错误;
故选:C.
3.【答案】B
解:A、一个三角形的两个角分别是40°、80°,则另一个内角为60°,而另一个三角形的两上角分别是60°、80°,这两个三角形相似;
B、一个三角形的三边长分别是4cm、6cm、8cm;另一个三角形的三边长分别是12cm、18cm、21cm,三边不成比例,这两个三角形不相似;
C、根据两边对应成比例且夹角相等知这两个三角形相似;
D、各有一个角是120°的两个等腰三角形,由于两个等腰三角形的底角均为30°,据此可知两个三角形相似;
故选:B.
4.【答案】B
【解答】
解:由正方形的性质可知,∠ACB=180°?45°=135°,
A、C、D图形中的钝角都不等于135°,
由勾股定理得,BC=2,AC=2,
对应的图形B中的边长分别为1和2,
∵12=22,
∴图B中的三角形(阴影部分)与△ABC相似,
故选B.
5.【答案】C
【解析】解:∵一个三角形的两个内角分别是40°,60°,
∴第三个内角为80°,
又∵另一个三角形的两个内角分别是40°,80°,
∴这两个三角形有两个内角相等,
∴这两个三角形相似.
6.【答案】C
较长的线段为全线段与较短线段的比例中项,这样的线段分割叫做黄金分割,他们的比值(
5?1
2
)叫做黄金比.
【解答】
解:∵P为线段AB的黄金分割点,且AP
故选C.
7.【答案】C
【解答】
解:A、∵∠A=∠A,∠ACP=∠B,
∴△ACP∽△ABC,
所以此选项的条件可以判定△ACP∽△ABC;
B、∵∠A=∠A,∠APC=∠ACB,
∴△ACP∽△ABC,
所以此选项的条件可以判定△ACP∽△ABC;
C、∵ACAB=CPBC,
当∠ACP=∠B时,△ACP∽△ABC,
所以此选项的条件不能判定△ACP∽△ABC;
D、∵ACAP=ABAC,
又∠A=∠A,
∴△ACP∽△ABC,
8.【答案】C
【解答】
解:∵∠A=∠A,
∴A.当∠B=∠C时,△ABE∽△ACD(两个对应角相等的两个三角形相似);
B.当∠ADC=∠AEB,△ABE∽△ACD(两个对应角相等的两个三角形相似);
C.当BE=CD,AB=AC时,无法证明△ABE和△ACD相似;
D.当AD:AC=AE:AB时,△ABE和△ACD相似(两组对应边成比例,且夹角相等的两个三角形相似).
故选C.
9.【答案】C
【解答】
解:∵∠BAC=∠D,ACAD=ABDE,
∴△ABC∽△DEA.
故选C.
10.【答案】A
【解答】
解:∵∠DAE=∠CAB,
∴当∠AED=∠B或∠ADE=∠C时,△ABC∽△AED;
当ADAC=AEAB即ADAE=ACAB时,△ABC∽△AED.
故选A.
11.【答案】B
利用相似三角形的判定定理,以及正方形的性质逐项判断即可.
【解答】
解:∵四边形ABCD为正方形,
∴AB=BC=CD,∠B=∠C=90°,
∵E为CD中点,
∴CD=2CE,即AB=BC=2CE,
①当∠APB=∠EPC时,结合∠B=∠C,可推出△ABP∽△ECP;
②当∠APE=∠APB≠60°时,则有∠APB≠∠EPC,所以不能推出△ABP∽△ECP;
③当P是BC中点时,则有BC=2PC,可知PC=CE,则△PCE为等腰直角三角形,而BP≠AB,即△ABP不是等腰直角三角形,故不能推出△ABP∽△ECP;
④当BP:BC=2:3时,则有BP:PC=2:1,且AB:CE=2:1,结合∠B=∠C,可推出△ABP∽△ECP.
故选B.
12.【答案】D
【解析】解:∵∠A=∠A,
∴当∠APC=∠ACB或∠ACP=∠B或AC:AB=AP:AC时,
△ACP∽△ABC.
13.【答案】C
【解答】
解:根据题意可知
选项A,三角形的顶角是75°,原?三角形的顶角是30°,对应角不相等,两个三角形不相似,故错误;
选项B,三角形是等边三角形,原三角形是顶角为30°的三角形,故不相似;故错误;
选项C,三角形是顶角为30°的等腰三角形,根据两边对应成比例,且夹角相等的两个三角形相似,便可以得到两个三角形相似,故正确;
选项D,三角形是顶角为32°的等腰三角形,原三角形的顶角是30°,与原三角形不相似,故错误.
故选C.
14.【答案】C
【解答】
解:∵四边形ABCD是平行四边形,
∴AD//BC,AB//CD,
∴△AFD∽△EFC∽△EAB.
故选C.
15.【答案】∠D=∠C或∠E=∠B或AEAB=ADAC
【解答】
解:∵∠1=∠2,
∴∠1+∠BAE=∠2+∠BAE,即∠DAE=∠CAB.
当∠D=∠C或∠E=∠B或AEAB=ADAC时,△ADE∽△ACB.
故答案为∠D=∠C或∠E=∠B或AEAB=ADAC.
16.【答案】3
【解答】
解:如图,
设AP为x,
∵AB=10,
∴PB=10?x,
①AD和PB是对应边时,
∵△APD与△BPC相似,
∴ADPB=APBC,
即410?x=x4,
整理得,x2?10x+16=0,
解得x1=2,x2=8,
②AD和BC是对应边时,
∵△APD与△BPC相似,
∴ADBC=APPB,
即44=x10?x,
解得x=5,
所以,当AP=2、5、8时,△APD与△BPC相似,
满足条件的点P有3个.
故答案为3.
17.【答案】2.4或1.5
∽△NMA两种情况进行讨论,再根据相似三角形的对应边成比例求解即可.
【解答】
解:当△ACD∽△MNA时,
则ADCD=MANA,
即63=t6?2t,
∴36?12t=3t.
∴t=2.4秒.
当△ACD∽△NMA时,
则ADCD=NAMA,
即63=6?2tt.
∴6t=18?6t.
∴t=1.5秒.
故答案为2.4或1.5.
18.【答案】3
【解答】
解:∵∠CPD=∠B,∠C=∠C,
∴△PCF∽△BCP.
∵∠CPD=∠A,∠D=∠D,
∴△APD∽△PGD.
∵∠CPD=∠A=∠B,∠APG=∠B+∠C,∠BFP=∠CPD+∠C,
∴∠APG=∠BFP,
∴△APG∽△BFP,
∴题图中有3对相似三角形.
故答案为3.
19.【答案】∠D=∠C或∠E=∠B或ADAC=AEAB
【解析】解:∵∠1=∠2,∴∠1+∠BAE=∠2+∠BAE,即∠DAE=∠CAB.
当∠D=∠C或∠E=∠B或ADAC=AEAB时,△ADE∽△ACB.
由∠1=∠2可得∠DAE=∠CAB.只需还有一对角对应相等或夹边对应成比例即可使得△ADE∽△ACB.
20.【答案】证明:∵AD=DB,
∴∠B=∠BAD.
∵∠BDA=∠1+∠C=∠2+∠ADE,
又∵∠1=∠2,
∴∠C=∠ADE.
∴△ABC∽△EAD.
21.【答案】解:设经x秒钟△PBQ与△ABC相似,
则AP=2xcm,BQ=4xcm,
∵AB=8cm,BC=16cm,
∴BP=AB?AP=(8?2x)cm,
∵∠B是公共角,
∵①当BPBA=BQBC,即8?2x8=4x16时,△PBQ∽△ABC,
解得:x=2;
②当BPBC=BQBA,即8?2x16=4x8时,△QBP∽△ABC,
解得:x=0.8,
∴经2或0.8秒钟△PBQ与△ABC相似.
22.【答案】证明:∵四边形ABCD是正方形,BP=3PC,Q是CD的中点,
∴QC=QD=12AD,CP=14AD,
∴ADQC=DQCP,
又∵∠ADQ=∠QCP,
∴△ADQ∽△QCP.
同课章节目录
- 第一章 特殊平行四边形
- 1 菱形的性质与判定
- 2 矩形的性质与判定
- 3 正方形的性质与判定
- 第二章 一元二次方程
- 1 认识一元二次方程
- 2 用配方法求解一元二次方程
- 3 用公式法求解一元二次方程
- 4 用因式分解法求解一元二次方程
- 5 一元二次方程的根与系数的关系
- 6 应用一元二次方程
- 第三章 概率的进一步认识
- 1 用树状图或表格求概率
- 2 用频率估计概率
- 第四章 图形的相似
- 1 成比例线段
- 2 平行线分线段成比例
- 3 相似多边形
- 4 探索三角形相似的条件
- 5 相似三角形判定定理的证明
- 6 利用相似三角形测高
- 7 相似三角形的性质
- 8 图形的位似
- 第五章 投影与视图
- 1 投影
- 2 视图
- 第六章 反比例函数
- 1 反比例函数
- 2 反比例函数的图象与性质
- 3 反比例函数的应用
