北师大版 九年级 上册 4.5 相似三角形判定定理的证明 练习 (Word版 含解析)
文档属性
| 名称 | 北师大版 九年级 上册 4.5 相似三角形判定定理的证明 练习 (Word版 含解析) |  | |
| 格式 | docx | ||
| 文件大小 | 184.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-12-24 23:30:39 | ||
图片预览

文档简介
相似三角形判定定理的证明练习
一、选择题
如图,在△ABC中,两条中线BE、CD相交于点O,则S△DOE:S△COB=(????)
A. 2 B. 12 C. 13 D. 14
小明想测量一棵树的高度,他发现树的影子恰好落在地面和一斜坡上;如图,此时测得地面上的影长为8米,坡面上的影长为4米.已知斜坡的坡角为30°,同一时刻,一根长为1米、垂直于地面放置的标杆在地面上的影长为2米,则树的高度为(????)
A. (6+3)米 B. 12米 C. (4+23)米 D. 10米
如图,已知在边长为12的正方形ABCD中,有一个小正方形EFGH,其中E、F、G分别在AB、BC、FD上.若BF=3,则BE长为(????)
A. 1 B. 2.5 C. 2.25 D. 1.5
如图,点A1、A2、B1、B2、C1、C2分别为△ABC的边BC、CA、AB的三等分点,若△ABC的周长为I,则六边形A1A2B1B2C1C2的周长为(????)
A. 2I B. 23I C. 33I D. 13I
如图,在平行四边形ABCD中,E为CD上一点,DE:CE=2:3,连结AE,BD交于点F,则S△DEF:S△ADF:S△ABF等于(????)
A. 2:3:5 B. 4:9:25 C. 4:10:25 D. 2:5:25
如图,在△ABC中,点D、E分别是AB、AC的中点,若△ADE的面积为4,则△ABC的面积为(? ? ? ?)
A. 8 B. 12 C. 14 D. 16
如图在△ABC中,点G是重心,连接BG并延长BG交AC于D,若点G到AB的距离为2,则点D到AB的距离是(????)
A. 2.5 B. 3 C. 3.6 D. 4
如图,已知AB、CD、EF都与BD垂直,垂足分别是B、D、F,且AB=1,CD=3,那么EF的长是(????)
A. 13 B. 23 C. 34 D. 45
如图,点F是?ABCD的边CD上一点,直线BF交AD的延长线于点E,则下列结论错误的是(????)
A. EDEA=DFAB B. DECB=EFFB C. BFBE=BCAE D. BCDE=BFBE
如图,△ABC中,BC=2,DE是它的中位线,下面三个结论:
(1)DE=1;
(2)△ADE∽△ABC;
(3)△ADE的面积与△ABC的面积之比为1:4.
其中正确的有(????)
A. 0个 B. 1个 C. 2个 D. 3个
如图,已知AD为△ABC的角平分线,DE//AB交AC于E,如果AEEC=35,那么ACAB等于(????)
A. 35 B. 53 C. 85 D. 32
如图,等边△ABC的边长为3,P为BC上一点,且BP=1,D为AC上一点,若∠APD=60°,则CD的长是(????)
A. 45 B. 34 C. 23 D. 12
如图,△ABC中,若DE//BC,EF//AB,则下列比例式正确的是(????)
A. ADDB=DEBC B. EFAD=BFBC C. EFAB=DEBC D. AEEC=BFFC
如图,在Rt△ABC内有边长分别为a,b,c的三个正方形,则a,b,c满足的关系式是(????)????
A. b=a+c B. b=ac C. b2=a2+c2 D. b=2a=2c
二、填空题
如图,已知点C为线段AB的中点,CD⊥AB且CD=AB=4,连接AD,BE⊥AB,AE是∠DAB的平分线,与DC相交于点F,EH⊥DC于点G,交AD于点H,则HG的长为______.
如图,矩形ABCD中,AB=2,BC=3,E是AD的中点,CF⊥BE于点F,则CF=______.
如图,在直角三角形ABC中(∠C=90°),放置边长分别3,4,x的三个正方形,则x的值为_____.
如图,在△ABC中,AD,BE是两条中线,则S△EDC:S△ABC=________.
如图,点P1,P2,P3,P4在坐标轴上,且,,若点P1,P2的坐标分别为,?2,0,则点P4的坐标为_______.
三、解答题
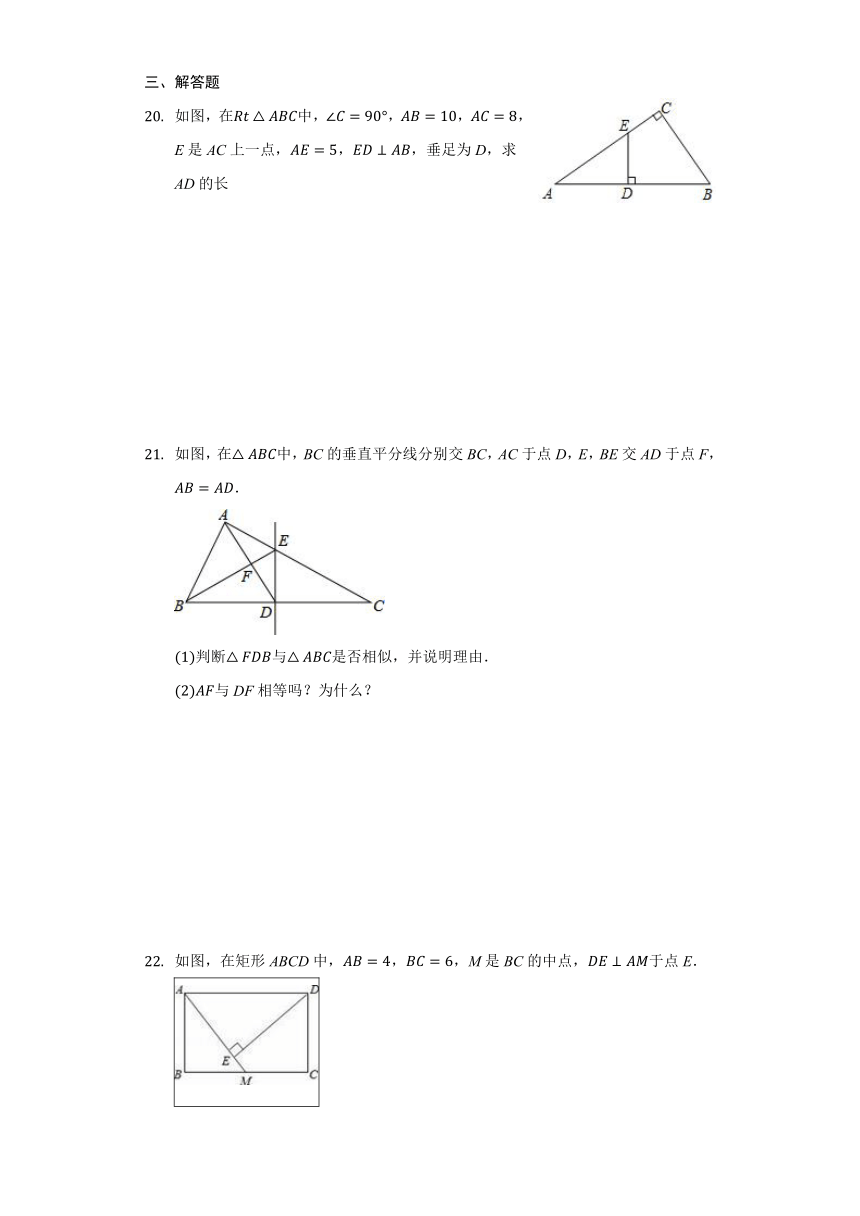
如图,在Rt△ABC中,∠C=90°,AB=10,AC=8,E是AC上一点,AE=5,ED⊥AB,垂足为D,求AD的长
如图,在△ABC中,BC的垂直平分线分别交BC,AC于点D,E,BE交AD于点F,AB=AD.
(1)判断△FDB与△ABC是否相似,并说明理由.
(2)AF与DF相等吗?为什么?
如图,在矩形ABCD中,AB=4,BC=6,M是BC的中点,DE⊥AM于点E.
(1)求证:△ADE∽△MAB;
(2)求DE的长.
答案和解析
1.【答案】D
【解答】
解:∵BE、CD是△ABC中的两条中线,
∴DE是△ABC的中位线,
于是DE//BC,DE=12BC
∴△DOE∽△COB,
∴S△DOES△COB=(DEBC)2=14
故选D.
2.【答案】A
【解答】
解:延长AC交BF延长线于D点,
则∠CFE=30°,作CE⊥BD于E,
在Rt△CFE中,∠CFE=30°,CF=4m,
∴CE=2(米),EF=CF2?CE2=23(米),
在Rt△CED中,
∵同一时刻,一根长为1米、垂直于地面放置的标杆在地面上的影长为2米,CE=2(米),CE:DE=1:2,
∴DE=4(米),
∴BD=BF+EF+ED=12+23(米)
在Rt△ABD中,AB=12BD=12(12+23)=(3+6)米.
故选A.
3.【答案】C
【解答】
解:∵四边形ABCD是正方形,
∴∠B=∠C=90°,BC=CD=12,
在△BEF与△CFD中,
∵∠BFE+∠CFD=∠CFD+∠CDF=90°,
∴∠BFE=∠CDF,
∴△BEF∽△CFD,
∴BFCD=BECF,
∵BF=3,BC=12,
∴CF=BC?BF=12?3=9,
∴312=BE9,
∴BE=2.25.
故选C.
4.【答案】B
【解析】解:∵点A1、A2,B1、B2,C1、C2分别是△ABC的边BC、CA、AB的三等分点,
∴△ABC∽△AC1B2,△ABC∽△C2BA1,△ABC∽△B1A2C,
∴C1B2:BC=1:3,C2A1:AC=1:3,B1A2:AB=1:3,
∴六边形A1A2B1B2C1C2的周长=23(AB+BC+CA),
∵△ABC的周长为I,
∴六边形A1A2B1B2C1C2的周长=23I.
5.【答案】C
【解析】解:∵四边形ABCD是平行四边形,
∴DC=AB,DC//AB,
∵DE:CE=2:3,
∴DE:AB=2:5,
∵DC//AB,
∴△DEF∽△BAF,
∴S△DEFS△ABF=(DEAB)2=425,EFAF=DEAB=25,
∴S△DEFS△ADF=EFAF=25=410(等高的三角形的面积之比等于对应边之比),
∴S△DEF:S△ADF:S△ABF等于4:10:25,
6.【答案】D
【解答】
解:∵在△ABC中,点D、E分别是AB、AC的中点,
∴DE//BC,DE=12BC,
∴△ADE∽△ABC,
∵DEBC=12,
,
∵△ADE的面积为4,
∴△ABC的面积为16,
故选D.
7.【答案】B
【解析】解:分别过D,G作GE⊥AB,DF⊥AB,
∵点G是△ABC的重心
∴BG=2DG
设DG=x,则GB=2x
∵GE⊥AB,DF⊥AB,∠ABD=∠ABD
∴△BGE∽△BDF
∴BGBG+GD=GEDF
即2x3x=2DF
∴DF=3.
8.【答案】C
【解答】
解:∵AB、CD、EF都与BD垂直,
∴AB//CD//EF,
∴△DEF∽△DAB,△BEF∽△BCD,
∴EFAB=DFDB,EFCD=BFBD,
∴EFAB+EFCD=DFDB+BFBD=BDBD=1,
∵AB=1,CD=3,
∴EF1+EF3=1,
∴EF=34.
故选C.
9.【答案】D
【解析】解:∵四边形ABCD是平行四边形,
∴CD//AB,AD//BC,CD=AB,AD=BC,
∴EDEA=DFAB,故A正确,选项不符合题意;
∴DECB=EFFB正确,B选项不符合题意;
BFBE=BCAE,正确,故C不符合题意;
∴BCDE=BFBE,错误,D符合题意.
10.【答案】D
【解析】解:(1)∵△ABC中,BC=2,DE是它的中位线,
∴DE=12BC
=12×2
=1
故本选项正确;
(2)∵△ABC中,DE是它的中位线
∴DE//BC
∴△ADE∽△ABC
故本选项正确;
(3)∵△ADE∽△ABC,相似比为1:2
∴△ADE的面积与△ABC的面积之比为1:4.
故本选项正确
11.【答案】B
【解析】
【解答】
解:∵DE//AB,
∴∠ADE=∠BAD,
∵AD为△ABC的角平分线,
∴∠DAE=∠BAD,
∴∠ADE=∠DAE,
∴AE=DE,
∵DE//AB,
∴△CDE∽△CBA,
∴DEAB=ECAC,
∴ACAB=ECDE,
∵AE=DE,
∴ACAB=ECDE=ECAE=53;
故选B.
12.【答案】C
【解答】
解:∵△ABC为等边三角形,
∴∠B=∠C=60°,
又∵∠APD+∠DPC=∠B+∠BAP,且∠APD=60°,
∴∠BAP=∠DPC,
∴△ABP∽△PCD,
∴BPCD=ABPC,
∵AB=BC=3,BP=1,
∴PC=2,
∴1CD=32,
∴CD=23.
故选:C.
13.【答案】D
【解析】解:∵DE//BC,EF//AB,
∴△ADE∽△ABC,△EFC∽△ABC,四边形BDEF为平行四边形,
∴△ADE∽△EFC,DE=BF,
∴AEEC=DEFC=BFFC.
14.【答案】A
【解答】
解:如图,
∵DH//AB//QF
∴∠EDH=∠A,∠GFQ=∠B;
又∵∠A+∠B=90°,∠EDH+∠DEH=90°,∠GFQ+∠FGQ=90°;
∴∠EDH=∠FGQ,∠DEH=∠GFQ;
∴△DHE∽△GQF,
∴DHGQ=EHFQ,
∴ab?c=b?ac,
∴ac=(b?c)(b?a)
∴b2=ab+bc=b(a+c),
∴b=a+c.
故选A.
15.【答案】3?5
【解析】解:∵AB=CD=4,C为线段AB的中点,
∴BC=AC=2,
∴AD=25,
∵EH⊥DC,CD⊥AB,BE⊥AB,
∴EH//AC,四边形BCGE为矩形,
∴∠HEA=∠EAB,BC=GE=2,
又∵AE是∠DAB的平分线,
∴∠EAB=∠DAE,
∴∠DAE=∠HEA,
∴HA=HE,
设GH=x,
则HA=HE=HG+GE=2+x,
∵EH//AC,
∴△DHG∽△DAC,
∴DHDA=HGAC,即25?(2+x)25=x2,
解得:x=3?5,
即HG=3?5,
16.【答案】2.4
【解答】
解:∵AD//BC,
∴∠AEB=∠CBF,
∵∠A=90°,∠CFB=90°,
∴△ABE∽△FCB,
∴ABFC=BEBC,
∵AB=2,BC=3,E是AD的中点,
∴BE=2.5,
∴2FC=2.53,
解得:FC=2.4.
故答案为:2.4.
17.【答案】7
【解析】解:如图∵在Rt△ABC中∠C=90°,放置边长分别3,4,x的三个正方形,
∴△CEF∽△OME∽△PFN,
∴OE:PN=OM:PF,
∵EF=x,MO=3,PN=4,
∴OE=x?3,PF=x?4,
∴(x?3):4=3:(x?4),
∴(x?3)(x?4)=12,
∴x1=0(不符合题意,舍去),x2=7.
18.【答案】1:4
【解答】
解:∵在△ABC中,AD,BE是两条中线,
∴DE//AB,DE=12AB,
∴△EDC∽△ABC,
,
故答案为1:4.
19.【答案】(8,0)
【解答】
解:∵点P1,P2的坐标分别为(0,?1),(?2,0),
∴OP1=1,OP2=2,
∵Rt△P1OP2∽Rt△P2OP3,
∴OP1OP2=OP2OP3,即12=2OP3,
解得,OP3=4,
∵Rt△P2OP3∽Rt△P3OP4,
∴OP2OP3=OP3OP4,即24=4OP4,
解得,OP4=8,
则点P4的坐标为(8,0),
故答案为:(8,0).
20.【答案】解:∵∠C=∠ADE=90°,∠A=∠A,
∴△ADE∽△ACB,
∴ADAC=AEAB
∴AD8=510,
∴AD=4.
21.【答案】解:(1)∵DE是BC垂直平分线,
∴BE=CE,
∴∠EBC=∠ECB,
∵AB=AD,
∴∠ABC=∠ADB,
∴△FDB∽△ABC;
(2)∵△FDB∽△ABC,
∴FDAB=BDBC=12,
∴AB=2FD,
∵AB=AD,
∴AD=2FD,
∴DF=AF.
22.【答案】(1)证明:∵四边形ABCD是矩形,
∴AD//BC,
∴∠DAE=∠AMB,
又∵∠DEA=∠B=90°,
∴△DAE∽△AMB;
(2)由(1)知△DAE∽△AMB,
∴DE:AD=AB:AM,
∵M是边BC的中点,BC=6,
∴BM=3,
又∵AB=4,∠B=90°,
∴AM=5,
∴DE:6=4:5,
∴DE=245.
一、选择题
如图,在△ABC中,两条中线BE、CD相交于点O,则S△DOE:S△COB=(????)
A. 2 B. 12 C. 13 D. 14
小明想测量一棵树的高度,他发现树的影子恰好落在地面和一斜坡上;如图,此时测得地面上的影长为8米,坡面上的影长为4米.已知斜坡的坡角为30°,同一时刻,一根长为1米、垂直于地面放置的标杆在地面上的影长为2米,则树的高度为(????)
A. (6+3)米 B. 12米 C. (4+23)米 D. 10米
如图,已知在边长为12的正方形ABCD中,有一个小正方形EFGH,其中E、F、G分别在AB、BC、FD上.若BF=3,则BE长为(????)
A. 1 B. 2.5 C. 2.25 D. 1.5
如图,点A1、A2、B1、B2、C1、C2分别为△ABC的边BC、CA、AB的三等分点,若△ABC的周长为I,则六边形A1A2B1B2C1C2的周长为(????)
A. 2I B. 23I C. 33I D. 13I
如图,在平行四边形ABCD中,E为CD上一点,DE:CE=2:3,连结AE,BD交于点F,则S△DEF:S△ADF:S△ABF等于(????)
A. 2:3:5 B. 4:9:25 C. 4:10:25 D. 2:5:25
如图,在△ABC中,点D、E分别是AB、AC的中点,若△ADE的面积为4,则△ABC的面积为(? ? ? ?)
A. 8 B. 12 C. 14 D. 16
如图在△ABC中,点G是重心,连接BG并延长BG交AC于D,若点G到AB的距离为2,则点D到AB的距离是(????)
A. 2.5 B. 3 C. 3.6 D. 4
如图,已知AB、CD、EF都与BD垂直,垂足分别是B、D、F,且AB=1,CD=3,那么EF的长是(????)
A. 13 B. 23 C. 34 D. 45
如图,点F是?ABCD的边CD上一点,直线BF交AD的延长线于点E,则下列结论错误的是(????)
A. EDEA=DFAB B. DECB=EFFB C. BFBE=BCAE D. BCDE=BFBE
如图,△ABC中,BC=2,DE是它的中位线,下面三个结论:
(1)DE=1;
(2)△ADE∽△ABC;
(3)△ADE的面积与△ABC的面积之比为1:4.
其中正确的有(????)
A. 0个 B. 1个 C. 2个 D. 3个
如图,已知AD为△ABC的角平分线,DE//AB交AC于E,如果AEEC=35,那么ACAB等于(????)
A. 35 B. 53 C. 85 D. 32
如图,等边△ABC的边长为3,P为BC上一点,且BP=1,D为AC上一点,若∠APD=60°,则CD的长是(????)
A. 45 B. 34 C. 23 D. 12
如图,△ABC中,若DE//BC,EF//AB,则下列比例式正确的是(????)
A. ADDB=DEBC B. EFAD=BFBC C. EFAB=DEBC D. AEEC=BFFC
如图,在Rt△ABC内有边长分别为a,b,c的三个正方形,则a,b,c满足的关系式是(????)????
A. b=a+c B. b=ac C. b2=a2+c2 D. b=2a=2c
二、填空题
如图,已知点C为线段AB的中点,CD⊥AB且CD=AB=4,连接AD,BE⊥AB,AE是∠DAB的平分线,与DC相交于点F,EH⊥DC于点G,交AD于点H,则HG的长为______.
如图,矩形ABCD中,AB=2,BC=3,E是AD的中点,CF⊥BE于点F,则CF=______.
如图,在直角三角形ABC中(∠C=90°),放置边长分别3,4,x的三个正方形,则x的值为_____.
如图,在△ABC中,AD,BE是两条中线,则S△EDC:S△ABC=________.
如图,点P1,P2,P3,P4在坐标轴上,且,,若点P1,P2的坐标分别为,?2,0,则点P4的坐标为_______.
三、解答题
如图,在Rt△ABC中,∠C=90°,AB=10,AC=8,E是AC上一点,AE=5,ED⊥AB,垂足为D,求AD的长
如图,在△ABC中,BC的垂直平分线分别交BC,AC于点D,E,BE交AD于点F,AB=AD.
(1)判断△FDB与△ABC是否相似,并说明理由.
(2)AF与DF相等吗?为什么?
如图,在矩形ABCD中,AB=4,BC=6,M是BC的中点,DE⊥AM于点E.
(1)求证:△ADE∽△MAB;
(2)求DE的长.
答案和解析
1.【答案】D
【解答】
解:∵BE、CD是△ABC中的两条中线,
∴DE是△ABC的中位线,
于是DE//BC,DE=12BC
∴△DOE∽△COB,
∴S△DOES△COB=(DEBC)2=14
故选D.
2.【答案】A
【解答】
解:延长AC交BF延长线于D点,
则∠CFE=30°,作CE⊥BD于E,
在Rt△CFE中,∠CFE=30°,CF=4m,
∴CE=2(米),EF=CF2?CE2=23(米),
在Rt△CED中,
∵同一时刻,一根长为1米、垂直于地面放置的标杆在地面上的影长为2米,CE=2(米),CE:DE=1:2,
∴DE=4(米),
∴BD=BF+EF+ED=12+23(米)
在Rt△ABD中,AB=12BD=12(12+23)=(3+6)米.
故选A.
3.【答案】C
【解答】
解:∵四边形ABCD是正方形,
∴∠B=∠C=90°,BC=CD=12,
在△BEF与△CFD中,
∵∠BFE+∠CFD=∠CFD+∠CDF=90°,
∴∠BFE=∠CDF,
∴△BEF∽△CFD,
∴BFCD=BECF,
∵BF=3,BC=12,
∴CF=BC?BF=12?3=9,
∴312=BE9,
∴BE=2.25.
故选C.
4.【答案】B
【解析】解:∵点A1、A2,B1、B2,C1、C2分别是△ABC的边BC、CA、AB的三等分点,
∴△ABC∽△AC1B2,△ABC∽△C2BA1,△ABC∽△B1A2C,
∴C1B2:BC=1:3,C2A1:AC=1:3,B1A2:AB=1:3,
∴六边形A1A2B1B2C1C2的周长=23(AB+BC+CA),
∵△ABC的周长为I,
∴六边形A1A2B1B2C1C2的周长=23I.
5.【答案】C
【解析】解:∵四边形ABCD是平行四边形,
∴DC=AB,DC//AB,
∵DE:CE=2:3,
∴DE:AB=2:5,
∵DC//AB,
∴△DEF∽△BAF,
∴S△DEFS△ABF=(DEAB)2=425,EFAF=DEAB=25,
∴S△DEFS△ADF=EFAF=25=410(等高的三角形的面积之比等于对应边之比),
∴S△DEF:S△ADF:S△ABF等于4:10:25,
6.【答案】D
【解答】
解:∵在△ABC中,点D、E分别是AB、AC的中点,
∴DE//BC,DE=12BC,
∴△ADE∽△ABC,
∵DEBC=12,
,
∵△ADE的面积为4,
∴△ABC的面积为16,
故选D.
7.【答案】B
【解析】解:分别过D,G作GE⊥AB,DF⊥AB,
∵点G是△ABC的重心
∴BG=2DG
设DG=x,则GB=2x
∵GE⊥AB,DF⊥AB,∠ABD=∠ABD
∴△BGE∽△BDF
∴BGBG+GD=GEDF
即2x3x=2DF
∴DF=3.
8.【答案】C
【解答】
解:∵AB、CD、EF都与BD垂直,
∴AB//CD//EF,
∴△DEF∽△DAB,△BEF∽△BCD,
∴EFAB=DFDB,EFCD=BFBD,
∴EFAB+EFCD=DFDB+BFBD=BDBD=1,
∵AB=1,CD=3,
∴EF1+EF3=1,
∴EF=34.
故选C.
9.【答案】D
【解析】解:∵四边形ABCD是平行四边形,
∴CD//AB,AD//BC,CD=AB,AD=BC,
∴EDEA=DFAB,故A正确,选项不符合题意;
∴DECB=EFFB正确,B选项不符合题意;
BFBE=BCAE,正确,故C不符合题意;
∴BCDE=BFBE,错误,D符合题意.
10.【答案】D
【解析】解:(1)∵△ABC中,BC=2,DE是它的中位线,
∴DE=12BC
=12×2
=1
故本选项正确;
(2)∵△ABC中,DE是它的中位线
∴DE//BC
∴△ADE∽△ABC
故本选项正确;
(3)∵△ADE∽△ABC,相似比为1:2
∴△ADE的面积与△ABC的面积之比为1:4.
故本选项正确
11.【答案】B
【解析】
【解答】
解:∵DE//AB,
∴∠ADE=∠BAD,
∵AD为△ABC的角平分线,
∴∠DAE=∠BAD,
∴∠ADE=∠DAE,
∴AE=DE,
∵DE//AB,
∴△CDE∽△CBA,
∴DEAB=ECAC,
∴ACAB=ECDE,
∵AE=DE,
∴ACAB=ECDE=ECAE=53;
故选B.
12.【答案】C
【解答】
解:∵△ABC为等边三角形,
∴∠B=∠C=60°,
又∵∠APD+∠DPC=∠B+∠BAP,且∠APD=60°,
∴∠BAP=∠DPC,
∴△ABP∽△PCD,
∴BPCD=ABPC,
∵AB=BC=3,BP=1,
∴PC=2,
∴1CD=32,
∴CD=23.
故选:C.
13.【答案】D
【解析】解:∵DE//BC,EF//AB,
∴△ADE∽△ABC,△EFC∽△ABC,四边形BDEF为平行四边形,
∴△ADE∽△EFC,DE=BF,
∴AEEC=DEFC=BFFC.
14.【答案】A
【解答】
解:如图,
∵DH//AB//QF
∴∠EDH=∠A,∠GFQ=∠B;
又∵∠A+∠B=90°,∠EDH+∠DEH=90°,∠GFQ+∠FGQ=90°;
∴∠EDH=∠FGQ,∠DEH=∠GFQ;
∴△DHE∽△GQF,
∴DHGQ=EHFQ,
∴ab?c=b?ac,
∴ac=(b?c)(b?a)
∴b2=ab+bc=b(a+c),
∴b=a+c.
故选A.
15.【答案】3?5
【解析】解:∵AB=CD=4,C为线段AB的中点,
∴BC=AC=2,
∴AD=25,
∵EH⊥DC,CD⊥AB,BE⊥AB,
∴EH//AC,四边形BCGE为矩形,
∴∠HEA=∠EAB,BC=GE=2,
又∵AE是∠DAB的平分线,
∴∠EAB=∠DAE,
∴∠DAE=∠HEA,
∴HA=HE,
设GH=x,
则HA=HE=HG+GE=2+x,
∵EH//AC,
∴△DHG∽△DAC,
∴DHDA=HGAC,即25?(2+x)25=x2,
解得:x=3?5,
即HG=3?5,
16.【答案】2.4
【解答】
解:∵AD//BC,
∴∠AEB=∠CBF,
∵∠A=90°,∠CFB=90°,
∴△ABE∽△FCB,
∴ABFC=BEBC,
∵AB=2,BC=3,E是AD的中点,
∴BE=2.5,
∴2FC=2.53,
解得:FC=2.4.
故答案为:2.4.
17.【答案】7
【解析】解:如图∵在Rt△ABC中∠C=90°,放置边长分别3,4,x的三个正方形,
∴△CEF∽△OME∽△PFN,
∴OE:PN=OM:PF,
∵EF=x,MO=3,PN=4,
∴OE=x?3,PF=x?4,
∴(x?3):4=3:(x?4),
∴(x?3)(x?4)=12,
∴x1=0(不符合题意,舍去),x2=7.
18.【答案】1:4
【解答】
解:∵在△ABC中,AD,BE是两条中线,
∴DE//AB,DE=12AB,
∴△EDC∽△ABC,
,
故答案为1:4.
19.【答案】(8,0)
【解答】
解:∵点P1,P2的坐标分别为(0,?1),(?2,0),
∴OP1=1,OP2=2,
∵Rt△P1OP2∽Rt△P2OP3,
∴OP1OP2=OP2OP3,即12=2OP3,
解得,OP3=4,
∵Rt△P2OP3∽Rt△P3OP4,
∴OP2OP3=OP3OP4,即24=4OP4,
解得,OP4=8,
则点P4的坐标为(8,0),
故答案为:(8,0).
20.【答案】解:∵∠C=∠ADE=90°,∠A=∠A,
∴△ADE∽△ACB,
∴ADAC=AEAB
∴AD8=510,
∴AD=4.
21.【答案】解:(1)∵DE是BC垂直平分线,
∴BE=CE,
∴∠EBC=∠ECB,
∵AB=AD,
∴∠ABC=∠ADB,
∴△FDB∽△ABC;
(2)∵△FDB∽△ABC,
∴FDAB=BDBC=12,
∴AB=2FD,
∵AB=AD,
∴AD=2FD,
∴DF=AF.
22.【答案】(1)证明:∵四边形ABCD是矩形,
∴AD//BC,
∴∠DAE=∠AMB,
又∵∠DEA=∠B=90°,
∴△DAE∽△AMB;
(2)由(1)知△DAE∽△AMB,
∴DE:AD=AB:AM,
∵M是边BC的中点,BC=6,
∴BM=3,
又∵AB=4,∠B=90°,
∴AM=5,
∴DE:6=4:5,
∴DE=245.
同课章节目录
- 第一章 特殊平行四边形
- 1 菱形的性质与判定
- 2 矩形的性质与判定
- 3 正方形的性质与判定
- 第二章 一元二次方程
- 1 认识一元二次方程
- 2 用配方法求解一元二次方程
- 3 用公式法求解一元二次方程
- 4 用因式分解法求解一元二次方程
- 5 一元二次方程的根与系数的关系
- 6 应用一元二次方程
- 第三章 概率的进一步认识
- 1 用树状图或表格求概率
- 2 用频率估计概率
- 第四章 图形的相似
- 1 成比例线段
- 2 平行线分线段成比例
- 3 相似多边形
- 4 探索三角形相似的条件
- 5 相似三角形判定定理的证明
- 6 利用相似三角形测高
- 7 相似三角形的性质
- 8 图形的位似
- 第五章 投影与视图
- 1 投影
- 2 视图
- 第六章 反比例函数
- 1 反比例函数
- 2 反比例函数的图象与性质
- 3 反比例函数的应用
