鲁教版 (五四制) 八年级 上册 5.4 多边形的内角和与外角和 练习(Word版 含解析)
文档属性
| 名称 | 鲁教版 (五四制) 八年级 上册 5.4 多边形的内角和与外角和 练习(Word版 含解析) |

|
|
| 格式 | docx | ||
| 文件大小 | 70.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 鲁教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-12-24 00:00:00 | ||
图片预览




文档简介
多边形的内角和与外角和练习
一、选择题
已知一个多边形的内角和是它的外角和的2倍,那么这个多边形的边数是
A. 3 B. 4 C. 5 D. 6
已知一个多边形的内角和为1080°,则这个多边形是(????)
A. 九边形 B. 八边形 C. 七边形 D. 六边形
一个多边形的内角和是它的外角和的2倍,则这个多边形是(????)
A. 五边形 B. 六边形 C. 七边形 D. 八边形
一个多边形的内角和是外角和的2倍,则这个多边形的边数为(????)
A. 4 B. 5 C. 6 D. 7
正五边形的每个外角等于(????)
A. 36° B. 60° C. 72° D. 108°
如图,A、B、C、D、E、F是平面上的6个点,则∠A+∠B+∠C+∠D+∠E+∠F的度数是(????)
A. 180° B. 360° C. 540° D. 720°
一个多边形的外角和是内角和的一半,则这个多边形的边数为(????)
A. 8 B. 7 C. 6 D. 5
正n边形每个内角的大小都为108°,则n=(????)
A. 5 B. 6 C. 7 D. 8
多边形的每个内角都等于150°,则从此多边形的一个顶点出发可作的对角线共有(????)
A. 8条 B. 9条 C. 10条 D. 11条
一个多边形从一个顶点可引对角线3条,这个多边形内角和等于(????)
A. 360° B. 540° C. 720° D. 900°
如图,已知四边形ABCD中,AD//BC,∠A=∠BCD=∠ABD,ED⊥CD,下列说法:①AB//CD;②DE平分∠ADB;③S△EDF=S△BCF;④∠CDF=∠CFD,其中正确的有(????)
A. ①②③ B. ①②④ C. ①③④ D. ①②③④
如果多边形的内角和是外角和的k倍,那么这个多边形的边数是(? ? )
A. k B. 2k+1 C. 2k+2 D. 2k?2
如图,在四边形ABCD中,∠A+∠D=α,∠ABC的平分线与∠BCD的平分线交于点P,则∠P=(????)
A. 90°?12α B. 12α C. 90°+12α D. 360°?α
若一个多边形的内角和度数为外角和的4倍,则这个多边形的边数为(????)
A. 12 B. 10 C. 9 D. 8
二、填空题
如图,∠1+∠2+∠3+∠4+∠5+∠6=________.
若一个多边形的内角和为540°,则这个多边形的边数为__________.
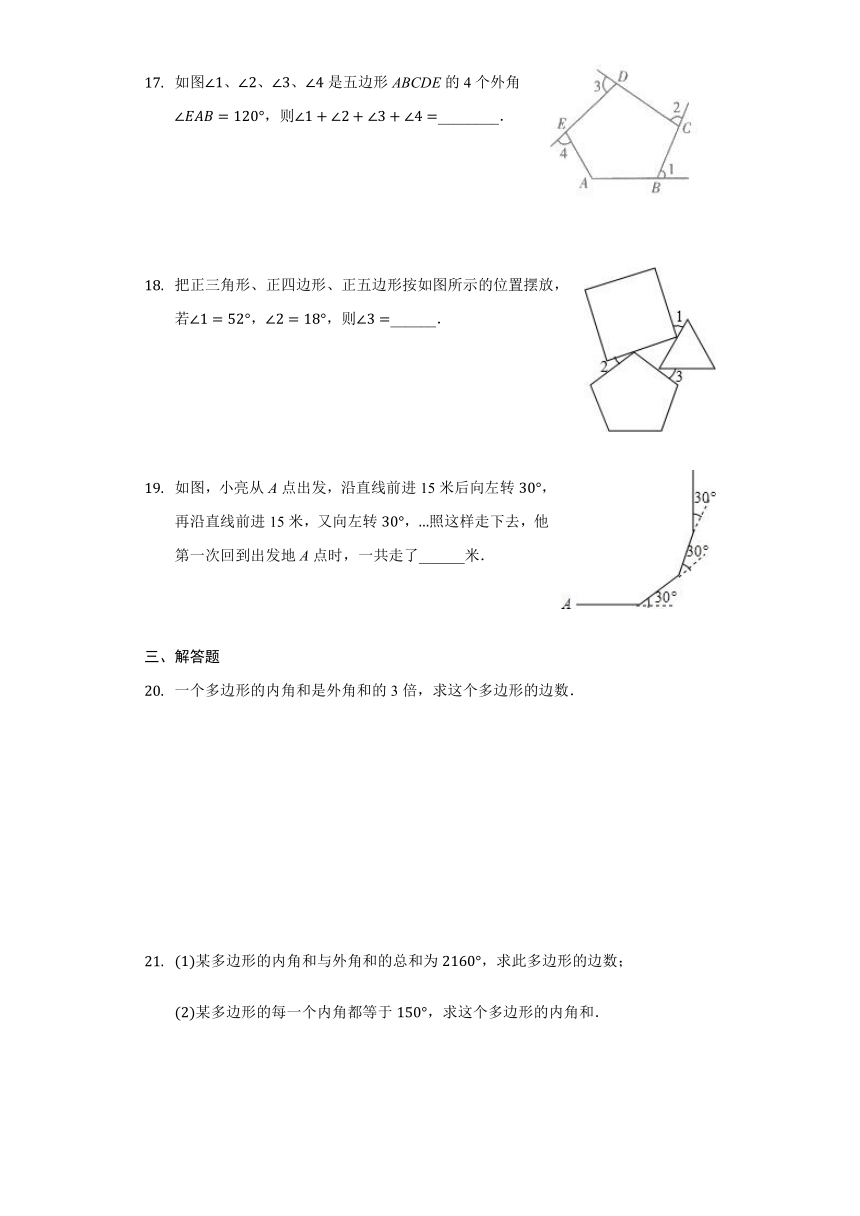
如图∠1、∠2、∠3、∠4是五边形ABCDE的4个外角∠EAB=120°,则∠1+∠2+∠3+∠4=________.
把正三角形、正四边形、正五边形按如图所示的位置摆放,若∠1=52°,∠2=18°,则∠3=______.
如图,小亮从A点出发,沿直线前进15米后向左转30°,再沿直线前进15米,又向左转30°,…照这样走下去,他第一次回到出发地A点时,一共走了______米.
三、解答题
一个多边形的内角和是外角和的3倍,求这个多边形的边数.
(1)某多边形的内角和与外角和的总和为2160°,求此多边形的边数;
(2)某多边形的每一个内角都等于150°,求这个多边形的内角和.
一个多边形的内角和是它的外角和的4倍,求这个多边形的边数.
答案和解析
1.【答案】D
【解答】
解:设这个多边形的边数为n,
∵n边形的内角和为(n?2)·180°,多边形的外角和为360°,
∴(n?2)·180°=360°×2,
解得n=6.
∴此多边形的边数为6.
故选D.
2.【答案】B
【解答】
解:根据n边形的内角和公式,得
(n?2)?180=1080,
解得n=8.
∴这个多边形的边数是8.
故选:B.
3.【答案】B
【解析】解:设这个多边形是n边形,根据题意,得
(n?2)×180°=2×360°,
解得:n=6.
故这个多边形是六边形.
4.【答案】C
【解答】
解:设这个多边形是n边形,
根据题意,得
(n?2)×180°=2×360°,
解得:n=6.
即这个多边形是六边形.
故选C.
5.【答案】C
【分析】
解:360°÷5=72°.
故正五边形的每个外角等于72°.
故选C.
6.【答案】B
【解答】
解:
∵∠BMQ=∠A+∠B,∠DQF=∠C+∠D,∠FNM=∠E+∠F,
∴∠BMQ+∠DQF+∠FNM=∠A+∠B+∠C+∠D+∠E+∠F,
∵∠BMQ+∠DQF+∠FNM=360°,
∴∠A+∠B+∠C+∠D+∠E+∠F=360°,
故选:B.
7.【答案】C
【解析】解:多边形的内角和是:2×360°=720°.
设多边形的边数是n,则
(n?2)?180=720,
解得:n=6.
即这个多边形的边数是6.
8.【答案】A
【解答】
解:∵正n边形每个内角的大小都为108°,
∴每个外角为:72°,
则n=360°72°=5.
故选A.
9.【答案】B
【解答】
解:∵多边形的每个内角都等于150°,
∴多边形的每个外角都等于180°?150°=30°,
∴边数n=360°÷30°=12,
∴对角线条数=12?3=9.
故选B.
10.【答案】C
【解答】
解:∵从一个顶点可引对角线3条,
∴多边形的边数为3+3=6.
多边形的内角和=(n?2)×180°=4×180°=720°.
故选:C.
11.【答案】A
【解析】解:∵AD//BC,
∴∠A+∠ABC=180°,∠ADC+∠BCD=180°,
∵∠A=∠BCD,
∴∠ABC=∠ADC,
∵∠A=∠BCD,
∴四边形ABCD是平行四边形,
∴AB//CD,
故①正确;
∵∠A=∠ABD,
∴AD=BD,
∵ED⊥CD,AB//CD,
∴DE⊥AB,
∴DE平分∠ADB,故②正确;
∵∠A=∠ABD,四边形ABCD是平行四边形,
∴AD=BD=BC,
∴∠BDC=∠BCD,
∵AD//BC,
∴∠ADB=∠DBC,
∵∠ADC=∠ADB+∠BDC,
∴∠ADC=∠DBC+∠BCD,
∴∠ADC?∠DCE=∠DBC+∠BCD?∠DCE=∠DBC+∠BCF,
∵∠DFC=∠DBC+∠BCF,
∴∠DFC=∠ADC?∠DCE,
∵∠CDF=∠ADC?∠ADB,∠DCE≠∠DBC,
∴∠CDF≠∠CFD.故④错误;
∵AB//CD,
∴△BED的边BE上的高和△EBC的边BE上的高相等,
∴由三角形面积公式得:S△BED=S△EBC,
都减去△EFB的面积得:S△EDF=S△BCF,故③正确;
12.【答案】C
【解答】
解:设这个多边形的边数是n,
则(n?2)?180°=k?360°,
解得n=2k+2.
故选:C.
13.【答案】B
【解析】解:∵四边形ABCD中,∠ABC+∠BCD=360°?(∠A+∠D)=360°?α,
∵PB和PC分别为∠ABC、∠BCD的平分线,
∴∠PBC+∠PCB=12(∠ABC+∠BCD)=12(360°?α)=180°?12α,
则∠P=180°?(∠PBC+∠PCB)=180°?(180°?12α)=12α.
14.【答案】B
【解析】解:设这个多边形的边数为n,
(n?2)?180°=4×360°,
解得n=10,
15.【答案】360°
【解析】
【解答】
解:如图,连接CD,构造出四边形ABCD,
显然有:∠1+∠4=∠7+∠8.
所以∠1+∠2+∠3+∠4+∠5+∠6
=∠2+∠3+∠5+∠6+∠7+∠8
=(4?2)×180°
=360°.
故答案为360°.
16.【答案】5
【解答】
解:设这个多边形的边数是n,
则(n?2)?180°=540°,
解得n=5,
故答案为5.
17.【答案】300°
【解析】【试题解析】
解:如图,
由题意得,∠5=180°?∠EAB=60°,
又∵多边形的外角和为360°,
∴∠1+∠2+∠3+∠4=360°?∠5=300°.
18.【答案】32°
【解答】
解:等边三角形的内角的度数是60°,正方形的内角度数是90°,正五边形的内角的度数是:15(5?2)×180°=108°,
则∠3=360°?60°?90°?108°?∠1?∠2=32°.
故答案为32°.
19.【答案】180
【解析】解:∵360÷30=12,
∴他需要走12次才会回到原来的起点,即一共走了15×12=180(米).
20.【答案】解:设这个多边形是n边形,由题意得:
(n?2)×180°=360°×3,
解得:n=8.
答:这个多边形的边数是8.
21.【答案】解:(1)根据题意,得
(n?2)?180=1800,
解得x=12.
所以此多边形的边数是12;
(2)因为每一个外角是180?150=30度,
所以边数是360÷30=12,
所以多边形的内角和是:(12?2)?180°=1800°.
22.【答案】解:设这个多边形的边数是,则
(n?2)×180=360×4,
n?2=8,
n=10.
答:这个多边形的边数是10.
一、选择题
已知一个多边形的内角和是它的外角和的2倍,那么这个多边形的边数是
A. 3 B. 4 C. 5 D. 6
已知一个多边形的内角和为1080°,则这个多边形是(????)
A. 九边形 B. 八边形 C. 七边形 D. 六边形
一个多边形的内角和是它的外角和的2倍,则这个多边形是(????)
A. 五边形 B. 六边形 C. 七边形 D. 八边形
一个多边形的内角和是外角和的2倍,则这个多边形的边数为(????)
A. 4 B. 5 C. 6 D. 7
正五边形的每个外角等于(????)
A. 36° B. 60° C. 72° D. 108°
如图,A、B、C、D、E、F是平面上的6个点,则∠A+∠B+∠C+∠D+∠E+∠F的度数是(????)
A. 180° B. 360° C. 540° D. 720°
一个多边形的外角和是内角和的一半,则这个多边形的边数为(????)
A. 8 B. 7 C. 6 D. 5
正n边形每个内角的大小都为108°,则n=(????)
A. 5 B. 6 C. 7 D. 8
多边形的每个内角都等于150°,则从此多边形的一个顶点出发可作的对角线共有(????)
A. 8条 B. 9条 C. 10条 D. 11条
一个多边形从一个顶点可引对角线3条,这个多边形内角和等于(????)
A. 360° B. 540° C. 720° D. 900°
如图,已知四边形ABCD中,AD//BC,∠A=∠BCD=∠ABD,ED⊥CD,下列说法:①AB//CD;②DE平分∠ADB;③S△EDF=S△BCF;④∠CDF=∠CFD,其中正确的有(????)
A. ①②③ B. ①②④ C. ①③④ D. ①②③④
如果多边形的内角和是外角和的k倍,那么这个多边形的边数是(? ? )
A. k B. 2k+1 C. 2k+2 D. 2k?2
如图,在四边形ABCD中,∠A+∠D=α,∠ABC的平分线与∠BCD的平分线交于点P,则∠P=(????)
A. 90°?12α B. 12α C. 90°+12α D. 360°?α
若一个多边形的内角和度数为外角和的4倍,则这个多边形的边数为(????)
A. 12 B. 10 C. 9 D. 8
二、填空题
如图,∠1+∠2+∠3+∠4+∠5+∠6=________.
若一个多边形的内角和为540°,则这个多边形的边数为__________.
如图∠1、∠2、∠3、∠4是五边形ABCDE的4个外角∠EAB=120°,则∠1+∠2+∠3+∠4=________.
把正三角形、正四边形、正五边形按如图所示的位置摆放,若∠1=52°,∠2=18°,则∠3=______.
如图,小亮从A点出发,沿直线前进15米后向左转30°,再沿直线前进15米,又向左转30°,…照这样走下去,他第一次回到出发地A点时,一共走了______米.
三、解答题
一个多边形的内角和是外角和的3倍,求这个多边形的边数.
(1)某多边形的内角和与外角和的总和为2160°,求此多边形的边数;
(2)某多边形的每一个内角都等于150°,求这个多边形的内角和.
一个多边形的内角和是它的外角和的4倍,求这个多边形的边数.
答案和解析
1.【答案】D
【解答】
解:设这个多边形的边数为n,
∵n边形的内角和为(n?2)·180°,多边形的外角和为360°,
∴(n?2)·180°=360°×2,
解得n=6.
∴此多边形的边数为6.
故选D.
2.【答案】B
【解答】
解:根据n边形的内角和公式,得
(n?2)?180=1080,
解得n=8.
∴这个多边形的边数是8.
故选:B.
3.【答案】B
【解析】解:设这个多边形是n边形,根据题意,得
(n?2)×180°=2×360°,
解得:n=6.
故这个多边形是六边形.
4.【答案】C
【解答】
解:设这个多边形是n边形,
根据题意,得
(n?2)×180°=2×360°,
解得:n=6.
即这个多边形是六边形.
故选C.
5.【答案】C
【分析】
解:360°÷5=72°.
故正五边形的每个外角等于72°.
故选C.
6.【答案】B
【解答】
解:
∵∠BMQ=∠A+∠B,∠DQF=∠C+∠D,∠FNM=∠E+∠F,
∴∠BMQ+∠DQF+∠FNM=∠A+∠B+∠C+∠D+∠E+∠F,
∵∠BMQ+∠DQF+∠FNM=360°,
∴∠A+∠B+∠C+∠D+∠E+∠F=360°,
故选:B.
7.【答案】C
【解析】解:多边形的内角和是:2×360°=720°.
设多边形的边数是n,则
(n?2)?180=720,
解得:n=6.
即这个多边形的边数是6.
8.【答案】A
【解答】
解:∵正n边形每个内角的大小都为108°,
∴每个外角为:72°,
则n=360°72°=5.
故选A.
9.【答案】B
【解答】
解:∵多边形的每个内角都等于150°,
∴多边形的每个外角都等于180°?150°=30°,
∴边数n=360°÷30°=12,
∴对角线条数=12?3=9.
故选B.
10.【答案】C
【解答】
解:∵从一个顶点可引对角线3条,
∴多边形的边数为3+3=6.
多边形的内角和=(n?2)×180°=4×180°=720°.
故选:C.
11.【答案】A
【解析】解:∵AD//BC,
∴∠A+∠ABC=180°,∠ADC+∠BCD=180°,
∵∠A=∠BCD,
∴∠ABC=∠ADC,
∵∠A=∠BCD,
∴四边形ABCD是平行四边形,
∴AB//CD,
故①正确;
∵∠A=∠ABD,
∴AD=BD,
∵ED⊥CD,AB//CD,
∴DE⊥AB,
∴DE平分∠ADB,故②正确;
∵∠A=∠ABD,四边形ABCD是平行四边形,
∴AD=BD=BC,
∴∠BDC=∠BCD,
∵AD//BC,
∴∠ADB=∠DBC,
∵∠ADC=∠ADB+∠BDC,
∴∠ADC=∠DBC+∠BCD,
∴∠ADC?∠DCE=∠DBC+∠BCD?∠DCE=∠DBC+∠BCF,
∵∠DFC=∠DBC+∠BCF,
∴∠DFC=∠ADC?∠DCE,
∵∠CDF=∠ADC?∠ADB,∠DCE≠∠DBC,
∴∠CDF≠∠CFD.故④错误;
∵AB//CD,
∴△BED的边BE上的高和△EBC的边BE上的高相等,
∴由三角形面积公式得:S△BED=S△EBC,
都减去△EFB的面积得:S△EDF=S△BCF,故③正确;
12.【答案】C
【解答】
解:设这个多边形的边数是n,
则(n?2)?180°=k?360°,
解得n=2k+2.
故选:C.
13.【答案】B
【解析】解:∵四边形ABCD中,∠ABC+∠BCD=360°?(∠A+∠D)=360°?α,
∵PB和PC分别为∠ABC、∠BCD的平分线,
∴∠PBC+∠PCB=12(∠ABC+∠BCD)=12(360°?α)=180°?12α,
则∠P=180°?(∠PBC+∠PCB)=180°?(180°?12α)=12α.
14.【答案】B
【解析】解:设这个多边形的边数为n,
(n?2)?180°=4×360°,
解得n=10,
15.【答案】360°
【解析】
【解答】
解:如图,连接CD,构造出四边形ABCD,
显然有:∠1+∠4=∠7+∠8.
所以∠1+∠2+∠3+∠4+∠5+∠6
=∠2+∠3+∠5+∠6+∠7+∠8
=(4?2)×180°
=360°.
故答案为360°.
16.【答案】5
【解答】
解:设这个多边形的边数是n,
则(n?2)?180°=540°,
解得n=5,
故答案为5.
17.【答案】300°
【解析】【试题解析】
解:如图,
由题意得,∠5=180°?∠EAB=60°,
又∵多边形的外角和为360°,
∴∠1+∠2+∠3+∠4=360°?∠5=300°.
18.【答案】32°
【解答】
解:等边三角形的内角的度数是60°,正方形的内角度数是90°,正五边形的内角的度数是:15(5?2)×180°=108°,
则∠3=360°?60°?90°?108°?∠1?∠2=32°.
故答案为32°.
19.【答案】180
【解析】解:∵360÷30=12,
∴他需要走12次才会回到原来的起点,即一共走了15×12=180(米).
20.【答案】解:设这个多边形是n边形,由题意得:
(n?2)×180°=360°×3,
解得:n=8.
答:这个多边形的边数是8.
21.【答案】解:(1)根据题意,得
(n?2)?180=1800,
解得x=12.
所以此多边形的边数是12;
(2)因为每一个外角是180?150=30度,
所以边数是360÷30=12,
所以多边形的内角和是:(12?2)?180°=1800°.
22.【答案】解:设这个多边形的边数是,则
(n?2)×180=360×4,
n?2=8,
n=10.
答:这个多边形的边数是10.
