鲁教版 (五四制)八年级 上册 5.3 三角形的中位线 练习 (Word版 含解析)
文档属性
| 名称 | 鲁教版 (五四制)八年级 上册 5.3 三角形的中位线 练习 (Word版 含解析) |
|
|
| 格式 | docx | ||
| 文件大小 | 223.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 鲁教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-12-24 00:00:00 | ||
图片预览



文档简介
三角形的中位线练习
一、选择题
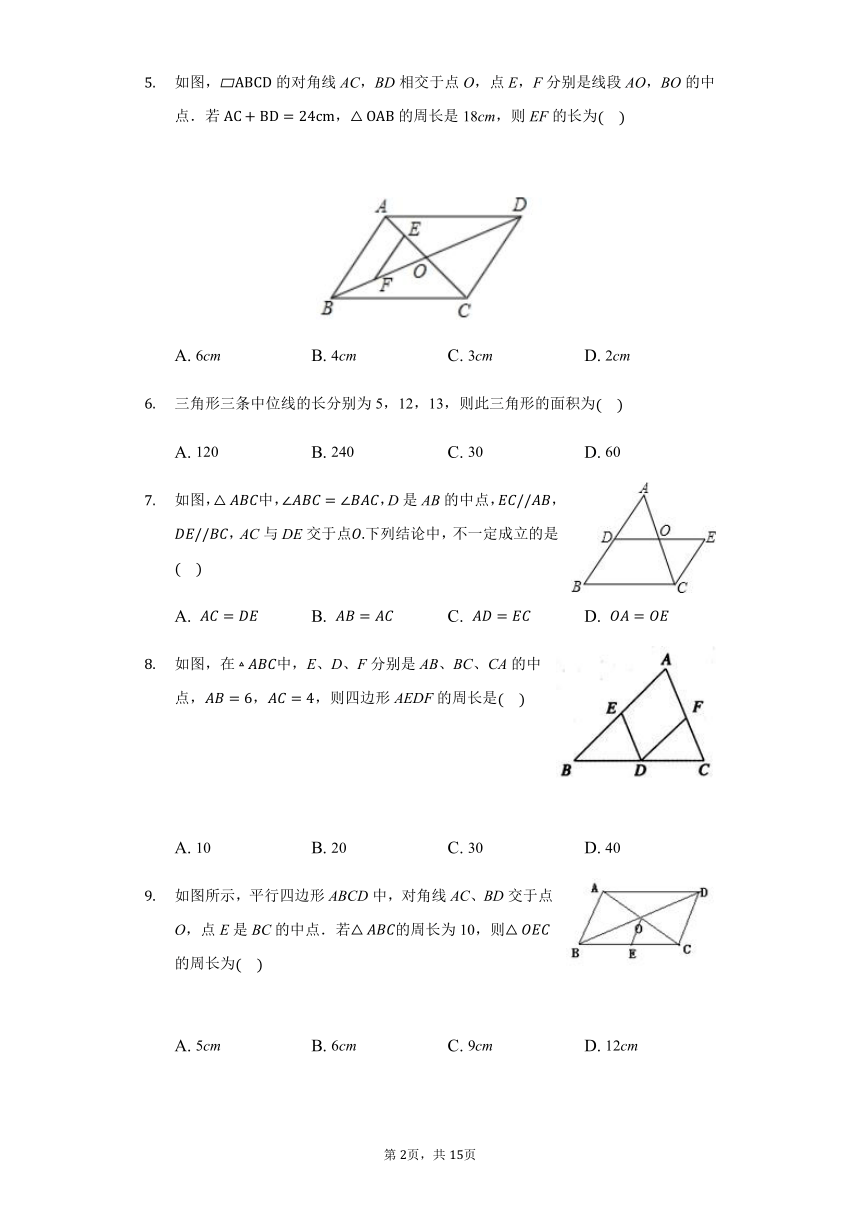
如图,平行四边形ABCD的周长为36,对角线AC、BD相交于点O,点E是CD的中点,BD=12,则△DOE的周长为(????)
A. 12 B. 15 C. 18 D. 21
如图,△ABC中,AB=4,AC=3,AD、AE分别是其角平分线和中线,过点C作CG⊥AD于F,交AB于G,连接EF,则线段EF的长为(????)
A. 12 B. 1 C. 72 D. 7
如图,在Rt△ABC中,∠A=30?,BC=1,点D,E分别是直角边BC,AC的中点,则DE的长为(????)
A. 1 B. 2 C. 3 D. 1+3
顺次连接矩形四边中点得到的四边形一定是(????)
A. 正方形 B. 矩形 C. 菱形 D. 等腰梯形
如图,?ABCD的对角线AC,BD相交于点O,点E,F分别是线段AO,BO的中点.若AC+BD=24cm,△OAB的周长是18cm,则EF的长为(????)
A. 6cm B. 4cm C. 3cm D. 2cm
三角形三条中位线的长分别为5,12,13,则此三角形的面积为(????)
A. 120 B. 240 C. 30 D. 60
如图,△ABC中,∠ABC=∠BAC,D是AB的中点,EC//AB,DE//BC,AC与DE交于点O.下列结论中,不一定成立的是(????)
A. AC=DE B. AB=AC C. AD=EC D. OA=OE
如图,在?ABC中,E、D、F分别是AB、BC、CA的中点,AB=6,AC=4,则四边形AEDF的周长是(????)
A. 10 B. 20 C. 30 D. 40
如图所示,平行四边形ABCD中,对角线AC、BD交于点O,点E是BC的中点.若△ABC的周长为10,则△OEC的周长为(????)
A. 5cm B. 6cm C. 9cm D. 12cm
如图,在△ABC中,点D、E分别是边AB、AC的中点,∠B=50°,∠A=26°,将△ABC沿DE折叠,点A的对应点是点A′,则∠AEA′的度数是(? ?)
A. 145° B. 152° C. 158° D. 160°
如图,平行四边形ABCD中,点E,F分别是AD,AB的中点,EF交AC于点G,那么AG:GC的值为(????)
A. 1:2 B. 1:3 C. 1:4 D. 2:3
已知三角形的三条中位线分别为3?cm,4?cm,6?cm,则这个三角形的周长为(????)
A. 13?cm B. 26?cm C. 24?cm D. 6.5?cm
如图,在等边三角形ABC中,中线AD、BE交于F,则图中共有等腰三角形共有(????)
A. 3个 B. 4个 C. 5个 D. 6个
如图,在Rt△ABC中,∠C=90°,AC=3,BC=4,点D,E,F分别为AB,AC,BC的中点,连结DE,EF,则四边形BDEF的周长为(????)
A. 7 B. 8 C. 9 D. 12
二、填空题
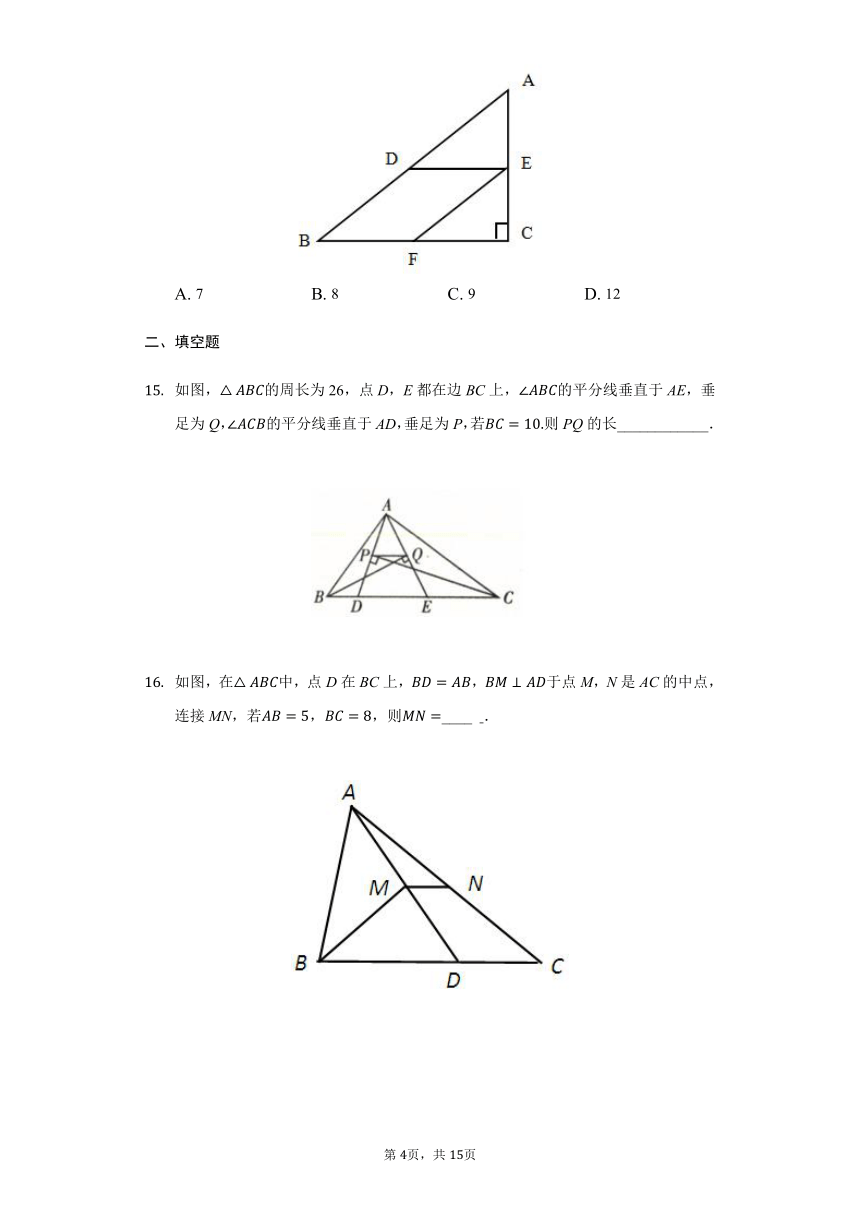
如图,△ABC的周长为26,点D,E都在边BC上,∠ABC的平分线垂直于AE,垂足为Q,∠ACB的平分线垂直于AD,垂足为P,若BC=10.则PQ的长____________.
如图,在△ABC中,点D在BC上,BD=AB,BM⊥AD于点M,N是AC的中点,连接MN,若AB=5,BC=8,则MN=____ ?.
如图,在?ABCD中,AD=6,点E、F分别是BD、CD的中点,则EF=_________.
在四边形ABCD中,对角线AC⊥BD且AC=6、BD=8,E、F分别是边AB、CD的中点,则EF=____.
三、解答题
在△ABC中,AB,BC,CA的中点分别是E,F,G,AD是高,求证:∠EDG=∠EFG.
已知:如图,在△ABC中,中线BE,CD交于点O,F,G分别是OB,OC的中点.求证:四边形DFGE是平行四边形.
如图所示,在四边形ABCD中,AB=CD,M、N、P分别是AD、BC、BD的中点,∠ABD=20°,∠BDC=70°,求∠PMN的度数.
在△ABC中,点M是边BC的中点,AD平分∠BAC,BD⊥AD,BD的延长线交AC于点E,AB=12,AC=20.
(1)求证:BD=DE;
(2)求DM的长.
答案和解析
1.【答案】B
【解答】
解:∵?ABCD的周长为36,
∴2(BC+CD)=36,则BC+CD=18.
∵四边形ABCD是平行四边形,对角线AC,BD相交于点O,BD=12,
∴OD=OB=12BD=6.
又∵点E是CD的中点,
∴OE是△BCD的中位线,DE=12CD,
∴OE=12BC,
∴△DOE的周长=OD+OE+DE=12BD+12(BC+CD)=6+9=15,
故选B.
2.【答案】A
【解答】
解:∵AD是∠BAC的平分线,
∴∠FAG=∠FAC,
∵CG⊥AD,
∴∠AFG=∠AFC=90°,
在△AFG和△AFC中,
∠FAG=∠FACAF=AF∠AFG=∠AFC,
∴△AFG≌△AFC(ASA),
∴FG=FC,AG=AC=3,
∴F是CG的中点,
又∵点E是BC的中点,
∴EF是△CBG的中位线,
∴EF=12BG=12(AB?AG)=12×(4?3)=12.
故选A.
3.【答案】A
【解答】
解:在Rt△ABC中,∵∠A=30?,BC=1,∴AB=2.
∵点D,E分别是BC,AC的中点,∴DE=12AB=12×2=1.
故选A.
4.【答案】C
【解析】解:连接AC、BD,
在△ABD中,
∵AH=HD,AE=EB
∴EH=12BD,
同理FG=12BD,HG=12AC,EF=12AC,
又∵在矩形ABCD中,AC=BD,
∴EH=HG=GF=FE,
∴四边形EFGH为菱形.
5.【答案】C
【解析】解:∵四边形ABCD是平行四边形,
∴OA=OC,OB=OD,
又∵AC+BD=24cm,
∴OA+OB=12cm,
∵△OAB的周长是18cm,
∴AB=6cm,
∵点E,F分别是线段AO,BO的中点,
∴EF是△OAB的中位线,
∴EF=12AB=3cm.
故选C.
6.【答案】A
【解答】
解:设中位线DE=5,DF=12,EF=13.
∵DE是△ABC的中位线,
∴BC=2DE=2×5=10.
同理:AC=2DF=2×12=24,AB=2EF=2×13=26.
∵102+242=676=262,
∴AC2+BC2=AB2,
∴△ABC是直角三角形,且∠ACB=90°,
∴S△ABC=12AC?BC=12×10×24=120.
故选A.
7.【答案】B
【解析】解:∵EC//AB,DE//BC,
∴四边形DBCE为平行四边形,
∴BC=DE,DB=EC,
∵∠ABC=∠BAC,
∴CB=CA,
∴AC=DE,A结论正确,不符合题意;
∵∠ABC与∠ACB不一定相等,
∴AB与AC不一定相等,B结论错误,符合题意;
∵AD=DB,DB=EC,
∴AD=EC,C结论正确,不符合题意;
∵DE//BC,
∴∠ADO=∠ABC,
∴∠ADO=∠A,
∴OA=OD,
∵DE//BC,D是AB的中点,
∴OD=12BC=12DE=OE,
∴OA=OE,D结论正确,不符合题意;
8.【答案】A
【解答】
解:∵在△ABC中,E、D、F分别是AB、BC、CA的中点,
∴DE=AF=12AC=2,DF=AE=12AB=3,
∴四边形AEDF的周长是(2+3)×2=10.
故选A.
9.【答案】A
【解答】
解:∵四边形ABCD是平行四边形,
∴OA=OC,OB=OD,
又∵E是BC中点,
∴OE是△ABC的中位线,BE=CE,
∴OE=12AB,
∴△OEC的周长=12△ABC的周长=12×10=5(cm),
故选A.
10.【答案】B
【解答】
解:∵D、E分别是AB、AC的中点,
∴DE//BC,
∴∠AED=∠C.
又∵∠C=180??(∠A+∠B)=104?,
∴∠AED=104?.
易得△AED≌△A′ED,
∴∠A′ED=∠AED=104?.
∴∠AEA′=360??∠A′ED?∠AED
=360??104??104?=152?.
故选B.
11.【答案】B
【解答】
解:连接BD,与AC相交于点O,∵点E,F分别是AD,AB的中点,
∴EF是△ABD的中位线,∴EF//DB,且EF=12DB,∴△AEF∽
△ADB,∴AGAO=EFDB=12,即G为AO的中点,∴AG=GO,又OA=OC,
∴AG:GC=1:3,
故选B.
12.【答案】B
【解答】
解:∵三角形的三条中位线长分别为3cm,4cm,6cm,
∴原三角形的三条边长分别为3cm×2=6cm,4cm×2=8cm,6cm×2=12cm,
∴原三角形的周长为6cm+8cm+12cm=26cm.
故选B.
13.【答案】D
【解答】
解:∵在等边三角形ABC中,中线AD、BE交于F,
∴AD⊥BC,BE⊥AC,∠ABE=∠CBE=∠BAD=∠CAD=30°,DE为△ABC中位线,
∴DE//AB,
∴∠BED=∠ADE=30°,∠EDC=60°,
∴∠BAF=∠FBA=30°,∠FDE=∠FED=30°,∠EAD=∠ADE=30°,∠DBE=∠DEB=30°,
∴△FAB,△FDE,△ADE,△BDE是等腰三角形,
∵∠EDC=∠C=60°,
∴△ABC,△DCE是等边三角形,
则图中共有等腰三角形共有6个.
故选D.
14.【答案】C
【解析】解:∵在Rt△ABC中,∠C=90°,AC=3,BC=4,
∴AB=BC2+AC2=5.
又∵点D,E分别为AB,AC的中点,
∴DE是△ABC的中位线,
∴DE=12BC=2.
同理,EF=12AB=2.5.
又BD=12AB=2.5,BF=12BC=2,
∴四边形BDEF的周长为:DE+EF+BF+BD=2+2.5+2+2.5=9.
15.【答案】3
【解答】
解:∵BQ平分∠ABC,BQ⊥AE,
∴△BAE是等腰三角形,同理△CAD是等腰三角形,
∴AB=BE,AC=CD,
∴BE+CD=AB+AC=26?BC=26?10=16,
∴DE=BE+CD?BC=6,
由题意得:点Q是AE中点,点P是AD中点(三线合一),
∴PQ是△ADE的中位线,
∴PQ=12DE=12×6=3.
故答案为3.
16.【答案】32
【解答】
解:∵BD=AB,BM⊥AD于点M,
∴AM=DM,
∵N是AC的中点,
∴AN=CN,
∴MN是三角形ADC的中位线,
∴MN=12DC,
∵AB=5,BC=8,
∴DC=3,
∴MN=32,
故答案为32.
17.【答案】3
【解答】
解:∵四边形ABCD是平行四边形,
∴BC=AD=6,
∵点E、F分别是BD、CD的中点,
∴EF=12BC=12×6=3.?
故答案为:3.
18.【答案】5
【解答】
解:如图,取BC的中点G,连接EG、FG,
∵E、F分别是边AB、CD的中点,
∴EG//AC且EG=12AC=12×6=3,
FG//BD且FG=12BD=12×8=4,
∵AC⊥BD,
∴EG⊥FG,
∴EF=??EG2+FG2?=??32+42=5.
故答案为:5.
19.【答案】证明:∵AD是高,且E是AB的中点,
∴DE=BE=AE,
∴∠B=∠BDE,∠EAD=∠ADE.
同理,∠DAG=∠ADG,∠CDG=∠C.
又∵AB、BC、CA的中点分别是E,F,G,
∴EF//AC,FG//AE,
∴四边形AEFG是平行四边形,
∴∠EFG=∠EAG=∠EAD+∠DAG=∠ADE+∠ADG=∠EDG,即:∠EDG=∠EFG.
20.【答案】解:在△ABC中,
∵BE、CD为中线
∴AD=BD,AE=CE,
∴DE//BC且DE=12BC.
在△OBC中,∵OF=FB,OG=GC,
∴FG//BC且FG=12BC.
∴DE//FG,DE=FG.
∴四边形DFGE为平行四边形.
21.【答案】解:∵在四边形ABCD中,M、N、P分别是AD、BC、BD的中点,
∴PN,PM分别是△CDB与△DAB的中位线,
∴PM=12AB,PN=12DC,PM//AB,PN//DC,
∵AB=CD,
∴PM=PN,
∴△PMN是等腰三角形,
∵PM//AB,PN//DC,
∴∠MPD=∠ABD=20°,∠BPN=∠BDC=70°,
∴∠MPN=∠MPD+∠NPD=20°+(180?70)°=130°,
∴∠PMN=180°?130°2=25°.
22.【答案】(1)证明:∵AD平分∠BAC,
∴∠BAD=∠DAE,
∵AD⊥BD,
∴∠ADB=∠ADE=90°,
在△ADB与△ADE中,
∠BAD=∠EADAD=AD∠ADB=∠ADE,
∴△ADB≌△ADE,
∴BD=DE;
(2)解:∵△ADB≌△ADE,
∴AE=AB=12,
∴EC=AC?AE=8,
∵M是BC的中点,BD=DE,
DM=12EC=4.
一、选择题
如图,平行四边形ABCD的周长为36,对角线AC、BD相交于点O,点E是CD的中点,BD=12,则△DOE的周长为(????)
A. 12 B. 15 C. 18 D. 21
如图,△ABC中,AB=4,AC=3,AD、AE分别是其角平分线和中线,过点C作CG⊥AD于F,交AB于G,连接EF,则线段EF的长为(????)
A. 12 B. 1 C. 72 D. 7
如图,在Rt△ABC中,∠A=30?,BC=1,点D,E分别是直角边BC,AC的中点,则DE的长为(????)
A. 1 B. 2 C. 3 D. 1+3
顺次连接矩形四边中点得到的四边形一定是(????)
A. 正方形 B. 矩形 C. 菱形 D. 等腰梯形
如图,?ABCD的对角线AC,BD相交于点O,点E,F分别是线段AO,BO的中点.若AC+BD=24cm,△OAB的周长是18cm,则EF的长为(????)
A. 6cm B. 4cm C. 3cm D. 2cm
三角形三条中位线的长分别为5,12,13,则此三角形的面积为(????)
A. 120 B. 240 C. 30 D. 60
如图,△ABC中,∠ABC=∠BAC,D是AB的中点,EC//AB,DE//BC,AC与DE交于点O.下列结论中,不一定成立的是(????)
A. AC=DE B. AB=AC C. AD=EC D. OA=OE
如图,在?ABC中,E、D、F分别是AB、BC、CA的中点,AB=6,AC=4,则四边形AEDF的周长是(????)
A. 10 B. 20 C. 30 D. 40
如图所示,平行四边形ABCD中,对角线AC、BD交于点O,点E是BC的中点.若△ABC的周长为10,则△OEC的周长为(????)
A. 5cm B. 6cm C. 9cm D. 12cm
如图,在△ABC中,点D、E分别是边AB、AC的中点,∠B=50°,∠A=26°,将△ABC沿DE折叠,点A的对应点是点A′,则∠AEA′的度数是(? ?)
A. 145° B. 152° C. 158° D. 160°
如图,平行四边形ABCD中,点E,F分别是AD,AB的中点,EF交AC于点G,那么AG:GC的值为(????)
A. 1:2 B. 1:3 C. 1:4 D. 2:3
已知三角形的三条中位线分别为3?cm,4?cm,6?cm,则这个三角形的周长为(????)
A. 13?cm B. 26?cm C. 24?cm D. 6.5?cm
如图,在等边三角形ABC中,中线AD、BE交于F,则图中共有等腰三角形共有(????)
A. 3个 B. 4个 C. 5个 D. 6个
如图,在Rt△ABC中,∠C=90°,AC=3,BC=4,点D,E,F分别为AB,AC,BC的中点,连结DE,EF,则四边形BDEF的周长为(????)
A. 7 B. 8 C. 9 D. 12
二、填空题
如图,△ABC的周长为26,点D,E都在边BC上,∠ABC的平分线垂直于AE,垂足为Q,∠ACB的平分线垂直于AD,垂足为P,若BC=10.则PQ的长____________.
如图,在△ABC中,点D在BC上,BD=AB,BM⊥AD于点M,N是AC的中点,连接MN,若AB=5,BC=8,则MN=____ ?.
如图,在?ABCD中,AD=6,点E、F分别是BD、CD的中点,则EF=_________.
在四边形ABCD中,对角线AC⊥BD且AC=6、BD=8,E、F分别是边AB、CD的中点,则EF=____.
三、解答题
在△ABC中,AB,BC,CA的中点分别是E,F,G,AD是高,求证:∠EDG=∠EFG.
已知:如图,在△ABC中,中线BE,CD交于点O,F,G分别是OB,OC的中点.求证:四边形DFGE是平行四边形.
如图所示,在四边形ABCD中,AB=CD,M、N、P分别是AD、BC、BD的中点,∠ABD=20°,∠BDC=70°,求∠PMN的度数.
在△ABC中,点M是边BC的中点,AD平分∠BAC,BD⊥AD,BD的延长线交AC于点E,AB=12,AC=20.
(1)求证:BD=DE;
(2)求DM的长.
答案和解析
1.【答案】B
【解答】
解:∵?ABCD的周长为36,
∴2(BC+CD)=36,则BC+CD=18.
∵四边形ABCD是平行四边形,对角线AC,BD相交于点O,BD=12,
∴OD=OB=12BD=6.
又∵点E是CD的中点,
∴OE是△BCD的中位线,DE=12CD,
∴OE=12BC,
∴△DOE的周长=OD+OE+DE=12BD+12(BC+CD)=6+9=15,
故选B.
2.【答案】A
【解答】
解:∵AD是∠BAC的平分线,
∴∠FAG=∠FAC,
∵CG⊥AD,
∴∠AFG=∠AFC=90°,
在△AFG和△AFC中,
∠FAG=∠FACAF=AF∠AFG=∠AFC,
∴△AFG≌△AFC(ASA),
∴FG=FC,AG=AC=3,
∴F是CG的中点,
又∵点E是BC的中点,
∴EF是△CBG的中位线,
∴EF=12BG=12(AB?AG)=12×(4?3)=12.
故选A.
3.【答案】A
【解答】
解:在Rt△ABC中,∵∠A=30?,BC=1,∴AB=2.
∵点D,E分别是BC,AC的中点,∴DE=12AB=12×2=1.
故选A.
4.【答案】C
【解析】解:连接AC、BD,
在△ABD中,
∵AH=HD,AE=EB
∴EH=12BD,
同理FG=12BD,HG=12AC,EF=12AC,
又∵在矩形ABCD中,AC=BD,
∴EH=HG=GF=FE,
∴四边形EFGH为菱形.
5.【答案】C
【解析】解:∵四边形ABCD是平行四边形,
∴OA=OC,OB=OD,
又∵AC+BD=24cm,
∴OA+OB=12cm,
∵△OAB的周长是18cm,
∴AB=6cm,
∵点E,F分别是线段AO,BO的中点,
∴EF是△OAB的中位线,
∴EF=12AB=3cm.
故选C.
6.【答案】A
【解答】
解:设中位线DE=5,DF=12,EF=13.
∵DE是△ABC的中位线,
∴BC=2DE=2×5=10.
同理:AC=2DF=2×12=24,AB=2EF=2×13=26.
∵102+242=676=262,
∴AC2+BC2=AB2,
∴△ABC是直角三角形,且∠ACB=90°,
∴S△ABC=12AC?BC=12×10×24=120.
故选A.
7.【答案】B
【解析】解:∵EC//AB,DE//BC,
∴四边形DBCE为平行四边形,
∴BC=DE,DB=EC,
∵∠ABC=∠BAC,
∴CB=CA,
∴AC=DE,A结论正确,不符合题意;
∵∠ABC与∠ACB不一定相等,
∴AB与AC不一定相等,B结论错误,符合题意;
∵AD=DB,DB=EC,
∴AD=EC,C结论正确,不符合题意;
∵DE//BC,
∴∠ADO=∠ABC,
∴∠ADO=∠A,
∴OA=OD,
∵DE//BC,D是AB的中点,
∴OD=12BC=12DE=OE,
∴OA=OE,D结论正确,不符合题意;
8.【答案】A
【解答】
解:∵在△ABC中,E、D、F分别是AB、BC、CA的中点,
∴DE=AF=12AC=2,DF=AE=12AB=3,
∴四边形AEDF的周长是(2+3)×2=10.
故选A.
9.【答案】A
【解答】
解:∵四边形ABCD是平行四边形,
∴OA=OC,OB=OD,
又∵E是BC中点,
∴OE是△ABC的中位线,BE=CE,
∴OE=12AB,
∴△OEC的周长=12△ABC的周长=12×10=5(cm),
故选A.
10.【答案】B
【解答】
解:∵D、E分别是AB、AC的中点,
∴DE//BC,
∴∠AED=∠C.
又∵∠C=180??(∠A+∠B)=104?,
∴∠AED=104?.
易得△AED≌△A′ED,
∴∠A′ED=∠AED=104?.
∴∠AEA′=360??∠A′ED?∠AED
=360??104??104?=152?.
故选B.
11.【答案】B
【解答】
解:连接BD,与AC相交于点O,∵点E,F分别是AD,AB的中点,
∴EF是△ABD的中位线,∴EF//DB,且EF=12DB,∴△AEF∽
△ADB,∴AGAO=EFDB=12,即G为AO的中点,∴AG=GO,又OA=OC,
∴AG:GC=1:3,
故选B.
12.【答案】B
【解答】
解:∵三角形的三条中位线长分别为3cm,4cm,6cm,
∴原三角形的三条边长分别为3cm×2=6cm,4cm×2=8cm,6cm×2=12cm,
∴原三角形的周长为6cm+8cm+12cm=26cm.
故选B.
13.【答案】D
【解答】
解:∵在等边三角形ABC中,中线AD、BE交于F,
∴AD⊥BC,BE⊥AC,∠ABE=∠CBE=∠BAD=∠CAD=30°,DE为△ABC中位线,
∴DE//AB,
∴∠BED=∠ADE=30°,∠EDC=60°,
∴∠BAF=∠FBA=30°,∠FDE=∠FED=30°,∠EAD=∠ADE=30°,∠DBE=∠DEB=30°,
∴△FAB,△FDE,△ADE,△BDE是等腰三角形,
∵∠EDC=∠C=60°,
∴△ABC,△DCE是等边三角形,
则图中共有等腰三角形共有6个.
故选D.
14.【答案】C
【解析】解:∵在Rt△ABC中,∠C=90°,AC=3,BC=4,
∴AB=BC2+AC2=5.
又∵点D,E分别为AB,AC的中点,
∴DE是△ABC的中位线,
∴DE=12BC=2.
同理,EF=12AB=2.5.
又BD=12AB=2.5,BF=12BC=2,
∴四边形BDEF的周长为:DE+EF+BF+BD=2+2.5+2+2.5=9.
15.【答案】3
【解答】
解:∵BQ平分∠ABC,BQ⊥AE,
∴△BAE是等腰三角形,同理△CAD是等腰三角形,
∴AB=BE,AC=CD,
∴BE+CD=AB+AC=26?BC=26?10=16,
∴DE=BE+CD?BC=6,
由题意得:点Q是AE中点,点P是AD中点(三线合一),
∴PQ是△ADE的中位线,
∴PQ=12DE=12×6=3.
故答案为3.
16.【答案】32
【解答】
解:∵BD=AB,BM⊥AD于点M,
∴AM=DM,
∵N是AC的中点,
∴AN=CN,
∴MN是三角形ADC的中位线,
∴MN=12DC,
∵AB=5,BC=8,
∴DC=3,
∴MN=32,
故答案为32.
17.【答案】3
【解答】
解:∵四边形ABCD是平行四边形,
∴BC=AD=6,
∵点E、F分别是BD、CD的中点,
∴EF=12BC=12×6=3.?
故答案为:3.
18.【答案】5
【解答】
解:如图,取BC的中点G,连接EG、FG,
∵E、F分别是边AB、CD的中点,
∴EG//AC且EG=12AC=12×6=3,
FG//BD且FG=12BD=12×8=4,
∵AC⊥BD,
∴EG⊥FG,
∴EF=??EG2+FG2?=??32+42=5.
故答案为:5.
19.【答案】证明:∵AD是高,且E是AB的中点,
∴DE=BE=AE,
∴∠B=∠BDE,∠EAD=∠ADE.
同理,∠DAG=∠ADG,∠CDG=∠C.
又∵AB、BC、CA的中点分别是E,F,G,
∴EF//AC,FG//AE,
∴四边形AEFG是平行四边形,
∴∠EFG=∠EAG=∠EAD+∠DAG=∠ADE+∠ADG=∠EDG,即:∠EDG=∠EFG.
20.【答案】解:在△ABC中,
∵BE、CD为中线
∴AD=BD,AE=CE,
∴DE//BC且DE=12BC.
在△OBC中,∵OF=FB,OG=GC,
∴FG//BC且FG=12BC.
∴DE//FG,DE=FG.
∴四边形DFGE为平行四边形.
21.【答案】解:∵在四边形ABCD中,M、N、P分别是AD、BC、BD的中点,
∴PN,PM分别是△CDB与△DAB的中位线,
∴PM=12AB,PN=12DC,PM//AB,PN//DC,
∵AB=CD,
∴PM=PN,
∴△PMN是等腰三角形,
∵PM//AB,PN//DC,
∴∠MPD=∠ABD=20°,∠BPN=∠BDC=70°,
∴∠MPN=∠MPD+∠NPD=20°+(180?70)°=130°,
∴∠PMN=180°?130°2=25°.
22.【答案】(1)证明:∵AD平分∠BAC,
∴∠BAD=∠DAE,
∵AD⊥BD,
∴∠ADB=∠ADE=90°,
在△ADB与△ADE中,
∠BAD=∠EADAD=AD∠ADB=∠ADE,
∴△ADB≌△ADE,
∴BD=DE;
(2)解:∵△ADB≌△ADE,
∴AE=AB=12,
∴EC=AC?AE=8,
∵M是BC的中点,BD=DE,
DM=12EC=4.
