2020-2021学年山东省聊城市莘县八年级上学期期中数学试卷(Word版 含解析)
文档属性
| 名称 | 2020-2021学年山东省聊城市莘县八年级上学期期中数学试卷(Word版 含解析) |  | |
| 格式 | doc | ||
| 文件大小 | 968.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 青岛版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-12-25 05:34:13 | ||
图片预览




文档简介
2020-2021学年山东省聊城市莘县八年级第一学期期中数学试卷
一、选择题
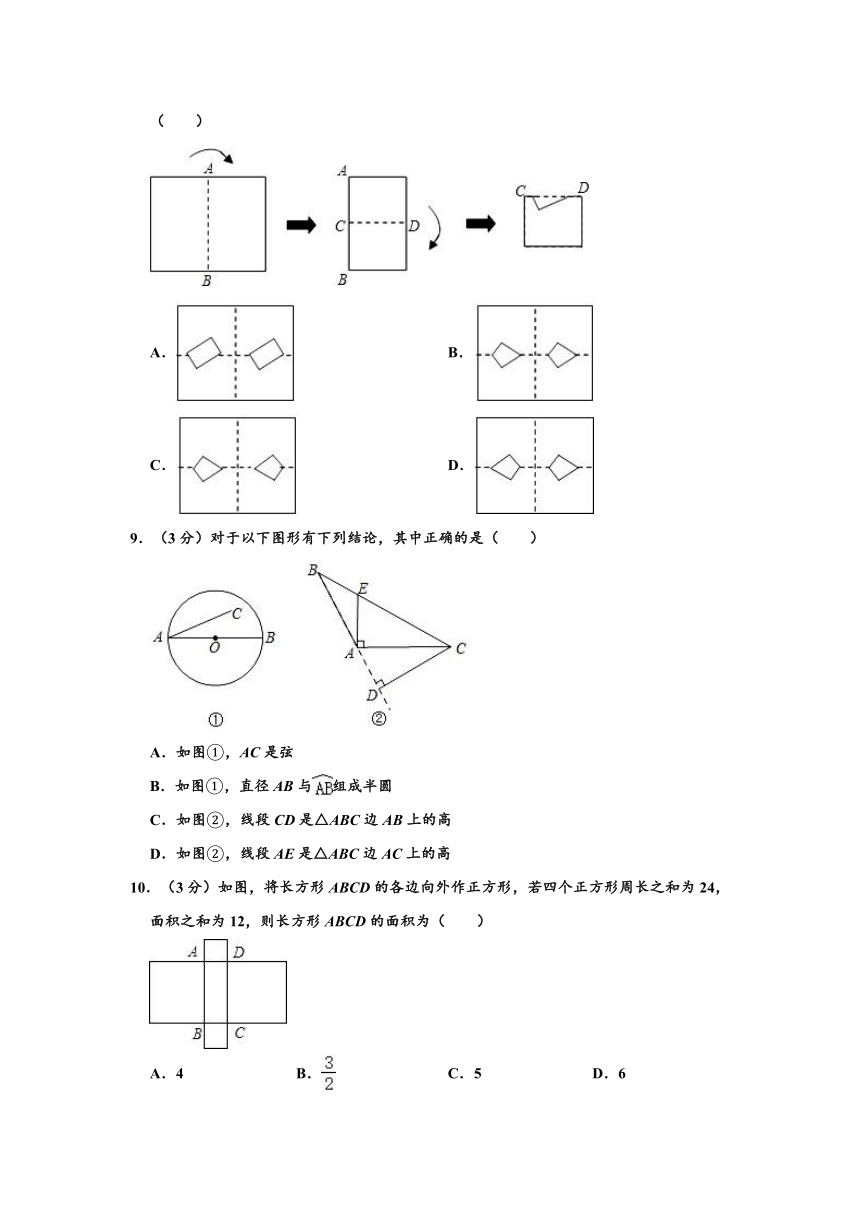
1.(3分)下列4个图案中,既是轴对称图形又是中心对称图形的有( )
A.1个 B.2个 C.3个 D.4个
2.(3分)如图是两个全等三角形,图中字母表示三角形的边长,则∠α的度数为( )
A.50° B.58° C.60° D.72°
3.(3分)若正多边形的一个外角是60°,则该正多边形的内角和为( )
A.360° B.540° C.720° D.900°
4.(3分)已知点A(2,a)与点B(b,3)关于x轴对称,则a+b的值为( )
A.﹣1 B.1 C.2 D.3
5.(3分)如图所示,为估计池塘两岸A,B间的距离,一位同学在池塘一侧选取了一点P,测得PA=16m,PB=12m,那么A,B间的距离不可能是( )
A.15m B.18m C.26m D.30m
6.(3分)若x2+2(m﹣5)x+16是完全平方式,则m的值是( )
A.5 B.9 C.9或1 D.5或1
7.(3分)已知a、b是△ABC的两边,且a2+b2=2ab,则△ABC的形状是( )
A.等腰三角形 B.等边三角形 C.锐角三角形 D.不确定
8.(3分)如图所示,将矩形纸片先沿虚线AB按箭头方向向右对折,接着对折后的纸片沿虚线CD向下对折,然后剪下一个小三角形,再将纸片打开,则打开后的展开图是( )
A. B.
C. D.
9.(3分)对于以下图形有下列结论,其中正确的是( )
A.如图①,AC是弦
B.如图①,直径AB与组成半圆
C.如图②,线段CD是△ABC边AB上的高
D.如图②,线段AE是△ABC边AC上的高
10.(3分)如图,将长方形ABCD的各边向外作正方形,若四个正方形周长之和为24,面积之和为12,则长方形ABCD的面积为( )
A.4 B. C.5 D.6
11.(3分)如图,大半圆中有n个小半圆,若大半圆弧长为L1,n个小半圆弧长的和为L2,大半圆的弦AB,BC,CD的长度和为L3.则( )
A.L1=L2>L3
B.L1=L2<L3
C.无法比较L1、L2、L3间的大小关系
D.L1>L3>L2
12.(3分)如图,矩形BCDE的各边分别平行于x轴或y轴,物体甲和物体乙由点(2,0)同时出发,沿矩形BCDE的边作环绕运动,物体甲按逆时针方向以1个单位/秒匀速运动,物体乙按顺时针方向以2个单位/秒匀速运动,则两个物体运动后的第2016次相遇地点的坐标是( )
A.(﹣1,﹣1) B.(2,0) C.(﹣1,1) D.(1,﹣1)
二、填空题(本大题共6小题,共18.0分)
13.(3分)已知点P(2m+4,m﹣1).
(1)若点P在x轴上,则点P的坐标为 ;
(2)若点P在第四象限,且到y轴的距离是2,则点P的坐标为 .
14.(3分)已知等腰三角形的一边等于3cm,另一边等于6cm,则周长为 cm.
15.(3分)已知点A(a﹣2,2a+7),点B的坐标为(1,5),直线AB∥y轴,则a的值是 .
16.(3分)如图,在△ABC中,AD⊥BC,AE平分∠BAC,若∠1=30°,∠2=20°,则∠B= .
17.(3分)如果x2+3x=2020,那么代数式x(2x+1)﹣(x﹣1)2的值为 .
18.(3分)王强同学用10块高度都是2cm的相同长方体小木块,垒了两堵与地面垂直的木墙,木墙之间刚好可以放进一个等腰直角三角板(AC=BC,∠ACB=90°),点C在DE上,点A和B分别与木墙的顶端重合,则两堵木墙之间的距离为 cm.
三、计算题(本大题共2小题,共12.0分)
19.(6分)因式分解:
(1)m2(m﹣1)+9(1﹣m).
(2)2x2y﹣8xy+8y.
20.(6分)先化简,再求值:(3x+2y)(3x﹣2y)﹣5x(x﹣y)﹣(2x﹣y)2,其中,y=﹣2.
四、解答题(本大题共5小题,共40.0分)
21.(8分)如图,在平面直角坐标系中,△ABC三个顶点的坐标分别为A(1,0),B(4,﹣2),C(5,3).
(1)在图中画出△ABC关于y轴的对称图形△A1B1C1;(要求:画出三角形,标出相应顶点的字母)
(2)分别写出△A1B1C1三个顶点的坐标,并计算△A1B1C1的面积.
22.(8分)如图,在平面直角坐标系中,每个小正方形的边长为1,点A的坐标为(﹣3,2).请按要求分别完成下列各小题:
(1)画出△ABC关于y轴对称的△A1B1C1,则点C1的坐标是 ;
(2)△ABC的面积是多少?
23.(8分)如图:AC∥EF,AC=EF,AE=BD.求证:△ABC≌△EDF.
24.(8分)复习“全等三角形”的知识时,老师布置了一道作业题:
“如图①,已知,在△ABC中,AB=AC,P是△ABC中内任意一点,将AP绕点A顺时针旋转至AQ,使∠QAP=∠BAC,连结BQ、CP则BQ=CP.”
小亮是个爱动脑筋的同学,他通过对图①的分析,证明了△ABQ≌△ACP,从而证得BQ=CP.之后,他将点P移到等腰三角形ABC外,原题中其它条件不变,发现“BQ=CP”仍然成立,请你就图②给出证明.
25.(8分)如图,在△ABC中,AB=AC,点D在边AC上,且BD=DA=BC.
(1)如图1,求∠A的度数;
(2)如图2,若M为线段AD上的点,过点M作直线MH⊥BD于点H,分别交直线AB,BC于点N,E.
①求证:△BNE是等腰三角形;
②试写出线段AN,CE,CD之间的数量关系,并加以证明.
参考答案
一、选择题(本大题共12小题,共36.0分)
1.(3分)下列4个图案中,既是轴对称图形又是中心对称图形的有( )
A.1个 B.2个 C.3个 D.4个
解:A、不是轴对称图形,也不是中心对称图形,不符合题意;
B、不是轴对称图形,是中心对称图形,不符合题意;
C、是轴对称图形,不是中心对称图形,不符合题意;
D、既是轴对称图形又是中心对称图形,符合题意.
故选:A.
2.(3分)如图是两个全等三角形,图中字母表示三角形的边长,则∠α的度数为( )
A.50° B.58° C.60° D.72°
解:根据三角形内角和可得∠β=180°﹣58°﹣72°=50°,
因为两个全等三角形,
所以∠α=∠β=50°,
故选:A.
3.(3分)若正多边形的一个外角是60°,则该正多边形的内角和为( )
A.360° B.540° C.720° D.900°
解:该正多边形的边数为:360°÷60°=6,
该正多边形的内角和为:(6﹣2)×180°=720°.
故选:C.
4.(3分)已知点A(2,a)与点B(b,3)关于x轴对称,则a+b的值为( )
A.﹣1 B.1 C.2 D.3
解:∵点A(2,a)与点B(b,3)关于x轴对称,
∴a=﹣3,b=2,
∴a+b=﹣3+2=﹣1.
故选:A.
5.(3分)如图所示,为估计池塘两岸A,B间的距离,一位同学在池塘一侧选取了一点P,测得PA=16m,PB=12m,那么A,B间的距离不可能是( )
A.15m B.18m C.26m D.30m
解:∵PA、PB、AB能构成三角形,
∴PA﹣PB<AB<PA+PB,即4m<AB<28m.
故选:D.
6.(3分)若x2+2(m﹣5)x+16是完全平方式,则m的值是( )
A.5 B.9 C.9或1 D.5或1
解:∵x2+2(m﹣5)x+16是完全平方式,
∴m﹣5=±4,
解得:m=9或1,
则m的值是9或1.
故选:C.
7.(3分)已知a、b是△ABC的两边,且a2+b2=2ab,则△ABC的形状是( )
A.等腰三角形 B.等边三角形 C.锐角三角形 D.不确定
解:∵a2+b2=2ab
(a﹣b)2=0
∴a=b,
又∵a、b为△ABC的两边,
∴△ABC是等腰三角形.
故选:A.
8.(3分)如图所示,将矩形纸片先沿虚线AB按箭头方向向右对折,接着对折后的纸片沿虚线CD向下对折,然后剪下一个小三角形,再将纸片打开,则打开后的展开图是( )
A. B.
C. D.
解:∵第三个图形是三角形,
∴将第三个图形展开,可得,即可排除答案A,
∵再展开可知两个短边正对着,
∴选择答案D,排除B与C.
故选:D.
9.(3分)对于以下图形有下列结论,其中正确的是( )
A.如图①,AC是弦
B.如图①,直径AB与组成半圆
C.如图②,线段CD是△ABC边AB上的高
D.如图②,线段AE是△ABC边AC上的高
解:A、AC不是弦,故错误;
B、半圆是弧,不包括弧所对的弦,故错误;
C、线段CD是△ABC边AB上的高,正确;
D、线段AE不是△ABC边AC上的高,故错误,
故选:C.
10.(3分)如图,将长方形ABCD的各边向外作正方形,若四个正方形周长之和为24,面积之和为12,则长方形ABCD的面积为( )
A.4 B. C.5 D.6
解:设AB=a,AD=b,由题意得,
8a+8b=24,2a2+2b2=12,
即a+b=3,a2+b2=6,
∴ab===,
即长方形ABCD的面积为,
故选:B.
11.(3分)如图,大半圆中有n个小半圆,若大半圆弧长为L1,n个小半圆弧长的和为L2,大半圆的弦AB,BC,CD的长度和为L3.则( )
A.L1=L2>L3
B.L1=L2<L3
C.无法比较L1、L2、L3间的大小关系
D.L1>L3>L2
解:设小半圆的半径为r,大半圆的半径为nr,L1==nπr,L2=×n=nπr,
∴L1=L2,
∵>弦AB,>弦BC,>弦CD,
∴L1>L3,
∴L1=L2>L3,
故选:A.
12.(3分)如图,矩形BCDE的各边分别平行于x轴或y轴,物体甲和物体乙由点(2,0)同时出发,沿矩形BCDE的边作环绕运动,物体甲按逆时针方向以1个单位/秒匀速运动,物体乙按顺时针方向以2个单位/秒匀速运动,则两个物体运动后的第2016次相遇地点的坐标是( )
A.(﹣1,﹣1) B.(2,0) C.(﹣1,1) D.(1,﹣1)
解:∵甲乙每相遇一次二者绕矩形BCDE运动了一圈,且乙的速度为甲的速度的2倍,
∴运动的每一圈中,甲运动了=圈,
∵2016÷3=672,
∴两个物体运动后的第2016次相遇时,甲物体运动了672圈,正好在出发点.
故选:B.
二、填空题(本大题共6小题,共18.0分)
13.(3分)已知点P(2m+4,m﹣1).
(1)若点P在x轴上,则点P的坐标为 (6,0) ;
(2)若点P在第四象限,且到y轴的距离是2,则点P的坐标为 (2,﹣2) .
解:(1)∵点P(2m+4,m﹣1),点P在x轴上,
∴m﹣1=0,
解得:m=1,
故2m+4=6,
∴点P的坐标为:(6,0);
(2)∵点P(2m+4,m﹣1),点P在第四象限,且到y轴的距离是2,
∴2m+4=2,
解得:m=﹣1,
故m﹣1=﹣2,
则点P的坐标为:(2,﹣2).
故答案为:(1)(6,0);(2)(2,﹣2).
14.(3分)已知等腰三角形的一边等于3cm,另一边等于6cm,则周长为 15 cm.
解:当3cm为腰,6cm为底时,
∵3+3=6,
∴不能构成三角形;
当腰为6时,
∵3+6>6,
∴能构成三角形,
∴等腰三角形的周长为:6+6+3=15cm.
故答案为:15.
15.(3分)已知点A(a﹣2,2a+7),点B的坐标为(1,5),直线AB∥y轴,则a的值是 3 .
解:∵点A(a﹣2,2a+7),点B的坐标为(1,5),直线AB∥y轴,
∴a﹣2=1,
解得a=3.
故答案是:3.
16.(3分)如图,在△ABC中,AD⊥BC,AE平分∠BAC,若∠1=30°,∠2=20°,则∠B= 50° .
解:∵AE平分∠BAC,
∴∠1=∠EAD+∠2,
∴∠EAD=∠1﹣∠2=30°﹣20°=10°,
Rt△ABD中,∠B=90°﹣∠BAD
=90°﹣30°﹣10°=50°.
故答案为50°.
17.(3分)如果x2+3x=2020,那么代数式x(2x+1)﹣(x﹣1)2的值为 2019 .
解:x(2x+1)﹣(x﹣1)2
=2x2+x﹣x2+2x﹣1
=x2+3x﹣1,
∵x2+3x=2020,
∴原式=2020﹣1
=2019,
故答案为:2019.
18.(3分)王强同学用10块高度都是2cm的相同长方体小木块,垒了两堵与地面垂直的木墙,木墙之间刚好可以放进一个等腰直角三角板(AC=BC,∠ACB=90°),点C在DE上,点A和B分别与木墙的顶端重合,则两堵木墙之间的距离为 20 cm.
解:由题意得:AC=BC,∠ACB=90°,AD⊥DE,BE⊥DE,
∴∠ADC=∠CEB=90°,
∴∠ACD+∠BCE=90°,∠ACD+∠DAC=90°,
∴∠BCE=∠DAC,
在△ADC和△CEB中,
,
∴△ADC≌△CEB(AAS);
由题意得:AD=EC=6cm,DC=BE=14cm,
∴DE=DC+CE=20(cm),
答:两堵木墙之间的距离为20cm.
故答案是:20.
三、计算题(本大题共2小题,共12.0分)
19.(6分)因式分解:
(1)m2(m﹣1)+9(1﹣m).
(2)2x2y﹣8xy+8y.
解:(1)m2(m﹣1)+9(1﹣m)
=m2(m﹣1)﹣9(m﹣1)
=(m﹣1)(m2﹣9)
=(m﹣1)(m﹣3)(m+3);
(2)2x2y﹣8xy+8y
=2y(x2﹣4x+4)
=2y(x﹣2)2.
20.(6分)先化简,再求值:(3x+2y)(3x﹣2y)﹣5x(x﹣y)﹣(2x﹣y)2,其中,y=﹣2.
解:原式=9x2﹣4y2﹣5x2+5xy﹣(4x2﹣4xy+y2)
=9x2﹣4y2﹣5x2+5xy﹣4x2+4xy﹣y2
=﹣5y2+9xy,
当,y=﹣2时,
原式==﹣20+6=﹣14.
四、解答题(本大题共5小题,共40.0分)
21.(8分)如图,在平面直角坐标系中,△ABC三个顶点的坐标分别为A(1,0),B(4,﹣2),C(5,3).
(1)在图中画出△ABC关于y轴的对称图形△A1B1C1;(要求:画出三角形,标出相应顶点的字母)
(2)分别写出△A1B1C1三个顶点的坐标,并计算△A1B1C1的面积.
解:(1)如图所示:
(2)A1(﹣1,0),B1(﹣4,﹣2),C(﹣5,3),
△A1B1C1的面积=.
22.(8分)如图,在平面直角坐标系中,每个小正方形的边长为1,点A的坐标为(﹣3,2).请按要求分别完成下列各小题:
(1)画出△ABC关于y轴对称的△A1B1C1,则点C1的坐标是 (5,3) ;
(2)△ABC的面积是多少?
解:(1)如图,△A1B1C1为所作;则点C1的坐标是(5,3);
故答案为(5,3);
(2)△ABC的面积=2×3﹣×1×2﹣×3×1﹣×1×2=2.5.
23.(8分)如图:AC∥EF,AC=EF,AE=BD.求证:△ABC≌△EDF.
【解答】证明:∵AC∥EF,
∴∠CAB=∠FED,
∵AE=BD,
∴AE+EB=BD+EB,
即AB=ED,
又∵AC=EF,
∴△ABC≌△EDF.
24.(8分)复习“全等三角形”的知识时,老师布置了一道作业题:
“如图①,已知,在△ABC中,AB=AC,P是△ABC中内任意一点,将AP绕点A顺时针旋转至AQ,使∠QAP=∠BAC,连结BQ、CP则BQ=CP.”
小亮是个爱动脑筋的同学,他通过对图①的分析,证明了△ABQ≌△ACP,从而证得BQ=CP.之后,他将点P移到等腰三角形ABC外,原题中其它条件不变,发现“BQ=CP”仍然成立,请你就图②给出证明.
【解答】证明:∵∠QAP=∠BAC
∴∠QAP+∠PAB=∠PAB+∠BAC
即∠QAB=∠PAC
在△ABQ和△ACP中,
,
∴△ABQ≌△ACP(SAS),
∴BQ=CP.
25.(8分)如图,在△ABC中,AB=AC,点D在边AC上,且BD=DA=BC.
(1)如图1,求∠A的度数;
(2)如图2,若M为线段AD上的点,过点M作直线MH⊥BD于点H,分别交直线AB,BC于点N,E.
①求证:△BNE是等腰三角形;
②试写出线段AN,CE,CD之间的数量关系,并加以证明.
解:(1)∵BD=BC,
∴∠BDC=∠C,
∵AB=AC,
∴∠ABC=∠C,
∴∠A=∠DBC,
∵AD=BD,
∴∠A=∠DBA,
∴∠A=∠DBA=∠DBC=∠ABC=∠C,
∵∠A+∠ABC+∠C=5∠A=180°,
∴∠A=36°;
(2)①∵∠A=∠ABD=36°,
∠B=∠C=72°,
∴∠ABD=∠CBD=36°,
∵BH⊥EN,
∴∠BHN=∠EHB=90°,
在△BNH与△BEH中,
,
∴△BNH≌△BEH,
∴BN=BE,
∴△BNE是等腰三角形;
②CD=AN+CE,
理由:由①知,BN=BE,
∵AB=AC,
∴AN=AB﹣BN=AC﹣BE,
∵CE=BE﹣BC,
∵CD=AC﹣AD=AC﹣BD=AC﹣BC,
∴CD=AN+CE.
一、选择题
1.(3分)下列4个图案中,既是轴对称图形又是中心对称图形的有( )
A.1个 B.2个 C.3个 D.4个
2.(3分)如图是两个全等三角形,图中字母表示三角形的边长,则∠α的度数为( )
A.50° B.58° C.60° D.72°
3.(3分)若正多边形的一个外角是60°,则该正多边形的内角和为( )
A.360° B.540° C.720° D.900°
4.(3分)已知点A(2,a)与点B(b,3)关于x轴对称,则a+b的值为( )
A.﹣1 B.1 C.2 D.3
5.(3分)如图所示,为估计池塘两岸A,B间的距离,一位同学在池塘一侧选取了一点P,测得PA=16m,PB=12m,那么A,B间的距离不可能是( )
A.15m B.18m C.26m D.30m
6.(3分)若x2+2(m﹣5)x+16是完全平方式,则m的值是( )
A.5 B.9 C.9或1 D.5或1
7.(3分)已知a、b是△ABC的两边,且a2+b2=2ab,则△ABC的形状是( )
A.等腰三角形 B.等边三角形 C.锐角三角形 D.不确定
8.(3分)如图所示,将矩形纸片先沿虚线AB按箭头方向向右对折,接着对折后的纸片沿虚线CD向下对折,然后剪下一个小三角形,再将纸片打开,则打开后的展开图是( )
A. B.
C. D.
9.(3分)对于以下图形有下列结论,其中正确的是( )
A.如图①,AC是弦
B.如图①,直径AB与组成半圆
C.如图②,线段CD是△ABC边AB上的高
D.如图②,线段AE是△ABC边AC上的高
10.(3分)如图,将长方形ABCD的各边向外作正方形,若四个正方形周长之和为24,面积之和为12,则长方形ABCD的面积为( )
A.4 B. C.5 D.6
11.(3分)如图,大半圆中有n个小半圆,若大半圆弧长为L1,n个小半圆弧长的和为L2,大半圆的弦AB,BC,CD的长度和为L3.则( )
A.L1=L2>L3
B.L1=L2<L3
C.无法比较L1、L2、L3间的大小关系
D.L1>L3>L2
12.(3分)如图,矩形BCDE的各边分别平行于x轴或y轴,物体甲和物体乙由点(2,0)同时出发,沿矩形BCDE的边作环绕运动,物体甲按逆时针方向以1个单位/秒匀速运动,物体乙按顺时针方向以2个单位/秒匀速运动,则两个物体运动后的第2016次相遇地点的坐标是( )
A.(﹣1,﹣1) B.(2,0) C.(﹣1,1) D.(1,﹣1)
二、填空题(本大题共6小题,共18.0分)
13.(3分)已知点P(2m+4,m﹣1).
(1)若点P在x轴上,则点P的坐标为 ;
(2)若点P在第四象限,且到y轴的距离是2,则点P的坐标为 .
14.(3分)已知等腰三角形的一边等于3cm,另一边等于6cm,则周长为 cm.
15.(3分)已知点A(a﹣2,2a+7),点B的坐标为(1,5),直线AB∥y轴,则a的值是 .
16.(3分)如图,在△ABC中,AD⊥BC,AE平分∠BAC,若∠1=30°,∠2=20°,则∠B= .
17.(3分)如果x2+3x=2020,那么代数式x(2x+1)﹣(x﹣1)2的值为 .
18.(3分)王强同学用10块高度都是2cm的相同长方体小木块,垒了两堵与地面垂直的木墙,木墙之间刚好可以放进一个等腰直角三角板(AC=BC,∠ACB=90°),点C在DE上,点A和B分别与木墙的顶端重合,则两堵木墙之间的距离为 cm.
三、计算题(本大题共2小题,共12.0分)
19.(6分)因式分解:
(1)m2(m﹣1)+9(1﹣m).
(2)2x2y﹣8xy+8y.
20.(6分)先化简,再求值:(3x+2y)(3x﹣2y)﹣5x(x﹣y)﹣(2x﹣y)2,其中,y=﹣2.
四、解答题(本大题共5小题,共40.0分)
21.(8分)如图,在平面直角坐标系中,△ABC三个顶点的坐标分别为A(1,0),B(4,﹣2),C(5,3).
(1)在图中画出△ABC关于y轴的对称图形△A1B1C1;(要求:画出三角形,标出相应顶点的字母)
(2)分别写出△A1B1C1三个顶点的坐标,并计算△A1B1C1的面积.
22.(8分)如图,在平面直角坐标系中,每个小正方形的边长为1,点A的坐标为(﹣3,2).请按要求分别完成下列各小题:
(1)画出△ABC关于y轴对称的△A1B1C1,则点C1的坐标是 ;
(2)△ABC的面积是多少?
23.(8分)如图:AC∥EF,AC=EF,AE=BD.求证:△ABC≌△EDF.
24.(8分)复习“全等三角形”的知识时,老师布置了一道作业题:
“如图①,已知,在△ABC中,AB=AC,P是△ABC中内任意一点,将AP绕点A顺时针旋转至AQ,使∠QAP=∠BAC,连结BQ、CP则BQ=CP.”
小亮是个爱动脑筋的同学,他通过对图①的分析,证明了△ABQ≌△ACP,从而证得BQ=CP.之后,他将点P移到等腰三角形ABC外,原题中其它条件不变,发现“BQ=CP”仍然成立,请你就图②给出证明.
25.(8分)如图,在△ABC中,AB=AC,点D在边AC上,且BD=DA=BC.
(1)如图1,求∠A的度数;
(2)如图2,若M为线段AD上的点,过点M作直线MH⊥BD于点H,分别交直线AB,BC于点N,E.
①求证:△BNE是等腰三角形;
②试写出线段AN,CE,CD之间的数量关系,并加以证明.
参考答案
一、选择题(本大题共12小题,共36.0分)
1.(3分)下列4个图案中,既是轴对称图形又是中心对称图形的有( )
A.1个 B.2个 C.3个 D.4个
解:A、不是轴对称图形,也不是中心对称图形,不符合题意;
B、不是轴对称图形,是中心对称图形,不符合题意;
C、是轴对称图形,不是中心对称图形,不符合题意;
D、既是轴对称图形又是中心对称图形,符合题意.
故选:A.
2.(3分)如图是两个全等三角形,图中字母表示三角形的边长,则∠α的度数为( )
A.50° B.58° C.60° D.72°
解:根据三角形内角和可得∠β=180°﹣58°﹣72°=50°,
因为两个全等三角形,
所以∠α=∠β=50°,
故选:A.
3.(3分)若正多边形的一个外角是60°,则该正多边形的内角和为( )
A.360° B.540° C.720° D.900°
解:该正多边形的边数为:360°÷60°=6,
该正多边形的内角和为:(6﹣2)×180°=720°.
故选:C.
4.(3分)已知点A(2,a)与点B(b,3)关于x轴对称,则a+b的值为( )
A.﹣1 B.1 C.2 D.3
解:∵点A(2,a)与点B(b,3)关于x轴对称,
∴a=﹣3,b=2,
∴a+b=﹣3+2=﹣1.
故选:A.
5.(3分)如图所示,为估计池塘两岸A,B间的距离,一位同学在池塘一侧选取了一点P,测得PA=16m,PB=12m,那么A,B间的距离不可能是( )
A.15m B.18m C.26m D.30m
解:∵PA、PB、AB能构成三角形,
∴PA﹣PB<AB<PA+PB,即4m<AB<28m.
故选:D.
6.(3分)若x2+2(m﹣5)x+16是完全平方式,则m的值是( )
A.5 B.9 C.9或1 D.5或1
解:∵x2+2(m﹣5)x+16是完全平方式,
∴m﹣5=±4,
解得:m=9或1,
则m的值是9或1.
故选:C.
7.(3分)已知a、b是△ABC的两边,且a2+b2=2ab,则△ABC的形状是( )
A.等腰三角形 B.等边三角形 C.锐角三角形 D.不确定
解:∵a2+b2=2ab
(a﹣b)2=0
∴a=b,
又∵a、b为△ABC的两边,
∴△ABC是等腰三角形.
故选:A.
8.(3分)如图所示,将矩形纸片先沿虚线AB按箭头方向向右对折,接着对折后的纸片沿虚线CD向下对折,然后剪下一个小三角形,再将纸片打开,则打开后的展开图是( )
A. B.
C. D.
解:∵第三个图形是三角形,
∴将第三个图形展开,可得,即可排除答案A,
∵再展开可知两个短边正对着,
∴选择答案D,排除B与C.
故选:D.
9.(3分)对于以下图形有下列结论,其中正确的是( )
A.如图①,AC是弦
B.如图①,直径AB与组成半圆
C.如图②,线段CD是△ABC边AB上的高
D.如图②,线段AE是△ABC边AC上的高
解:A、AC不是弦,故错误;
B、半圆是弧,不包括弧所对的弦,故错误;
C、线段CD是△ABC边AB上的高,正确;
D、线段AE不是△ABC边AC上的高,故错误,
故选:C.
10.(3分)如图,将长方形ABCD的各边向外作正方形,若四个正方形周长之和为24,面积之和为12,则长方形ABCD的面积为( )
A.4 B. C.5 D.6
解:设AB=a,AD=b,由题意得,
8a+8b=24,2a2+2b2=12,
即a+b=3,a2+b2=6,
∴ab===,
即长方形ABCD的面积为,
故选:B.
11.(3分)如图,大半圆中有n个小半圆,若大半圆弧长为L1,n个小半圆弧长的和为L2,大半圆的弦AB,BC,CD的长度和为L3.则( )
A.L1=L2>L3
B.L1=L2<L3
C.无法比较L1、L2、L3间的大小关系
D.L1>L3>L2
解:设小半圆的半径为r,大半圆的半径为nr,L1==nπr,L2=×n=nπr,
∴L1=L2,
∵>弦AB,>弦BC,>弦CD,
∴L1>L3,
∴L1=L2>L3,
故选:A.
12.(3分)如图,矩形BCDE的各边分别平行于x轴或y轴,物体甲和物体乙由点(2,0)同时出发,沿矩形BCDE的边作环绕运动,物体甲按逆时针方向以1个单位/秒匀速运动,物体乙按顺时针方向以2个单位/秒匀速运动,则两个物体运动后的第2016次相遇地点的坐标是( )
A.(﹣1,﹣1) B.(2,0) C.(﹣1,1) D.(1,﹣1)
解:∵甲乙每相遇一次二者绕矩形BCDE运动了一圈,且乙的速度为甲的速度的2倍,
∴运动的每一圈中,甲运动了=圈,
∵2016÷3=672,
∴两个物体运动后的第2016次相遇时,甲物体运动了672圈,正好在出发点.
故选:B.
二、填空题(本大题共6小题,共18.0分)
13.(3分)已知点P(2m+4,m﹣1).
(1)若点P在x轴上,则点P的坐标为 (6,0) ;
(2)若点P在第四象限,且到y轴的距离是2,则点P的坐标为 (2,﹣2) .
解:(1)∵点P(2m+4,m﹣1),点P在x轴上,
∴m﹣1=0,
解得:m=1,
故2m+4=6,
∴点P的坐标为:(6,0);
(2)∵点P(2m+4,m﹣1),点P在第四象限,且到y轴的距离是2,
∴2m+4=2,
解得:m=﹣1,
故m﹣1=﹣2,
则点P的坐标为:(2,﹣2).
故答案为:(1)(6,0);(2)(2,﹣2).
14.(3分)已知等腰三角形的一边等于3cm,另一边等于6cm,则周长为 15 cm.
解:当3cm为腰,6cm为底时,
∵3+3=6,
∴不能构成三角形;
当腰为6时,
∵3+6>6,
∴能构成三角形,
∴等腰三角形的周长为:6+6+3=15cm.
故答案为:15.
15.(3分)已知点A(a﹣2,2a+7),点B的坐标为(1,5),直线AB∥y轴,则a的值是 3 .
解:∵点A(a﹣2,2a+7),点B的坐标为(1,5),直线AB∥y轴,
∴a﹣2=1,
解得a=3.
故答案是:3.
16.(3分)如图,在△ABC中,AD⊥BC,AE平分∠BAC,若∠1=30°,∠2=20°,则∠B= 50° .
解:∵AE平分∠BAC,
∴∠1=∠EAD+∠2,
∴∠EAD=∠1﹣∠2=30°﹣20°=10°,
Rt△ABD中,∠B=90°﹣∠BAD
=90°﹣30°﹣10°=50°.
故答案为50°.
17.(3分)如果x2+3x=2020,那么代数式x(2x+1)﹣(x﹣1)2的值为 2019 .
解:x(2x+1)﹣(x﹣1)2
=2x2+x﹣x2+2x﹣1
=x2+3x﹣1,
∵x2+3x=2020,
∴原式=2020﹣1
=2019,
故答案为:2019.
18.(3分)王强同学用10块高度都是2cm的相同长方体小木块,垒了两堵与地面垂直的木墙,木墙之间刚好可以放进一个等腰直角三角板(AC=BC,∠ACB=90°),点C在DE上,点A和B分别与木墙的顶端重合,则两堵木墙之间的距离为 20 cm.
解:由题意得:AC=BC,∠ACB=90°,AD⊥DE,BE⊥DE,
∴∠ADC=∠CEB=90°,
∴∠ACD+∠BCE=90°,∠ACD+∠DAC=90°,
∴∠BCE=∠DAC,
在△ADC和△CEB中,
,
∴△ADC≌△CEB(AAS);
由题意得:AD=EC=6cm,DC=BE=14cm,
∴DE=DC+CE=20(cm),
答:两堵木墙之间的距离为20cm.
故答案是:20.
三、计算题(本大题共2小题,共12.0分)
19.(6分)因式分解:
(1)m2(m﹣1)+9(1﹣m).
(2)2x2y﹣8xy+8y.
解:(1)m2(m﹣1)+9(1﹣m)
=m2(m﹣1)﹣9(m﹣1)
=(m﹣1)(m2﹣9)
=(m﹣1)(m﹣3)(m+3);
(2)2x2y﹣8xy+8y
=2y(x2﹣4x+4)
=2y(x﹣2)2.
20.(6分)先化简,再求值:(3x+2y)(3x﹣2y)﹣5x(x﹣y)﹣(2x﹣y)2,其中,y=﹣2.
解:原式=9x2﹣4y2﹣5x2+5xy﹣(4x2﹣4xy+y2)
=9x2﹣4y2﹣5x2+5xy﹣4x2+4xy﹣y2
=﹣5y2+9xy,
当,y=﹣2时,
原式==﹣20+6=﹣14.
四、解答题(本大题共5小题,共40.0分)
21.(8分)如图,在平面直角坐标系中,△ABC三个顶点的坐标分别为A(1,0),B(4,﹣2),C(5,3).
(1)在图中画出△ABC关于y轴的对称图形△A1B1C1;(要求:画出三角形,标出相应顶点的字母)
(2)分别写出△A1B1C1三个顶点的坐标,并计算△A1B1C1的面积.
解:(1)如图所示:
(2)A1(﹣1,0),B1(﹣4,﹣2),C(﹣5,3),
△A1B1C1的面积=.
22.(8分)如图,在平面直角坐标系中,每个小正方形的边长为1,点A的坐标为(﹣3,2).请按要求分别完成下列各小题:
(1)画出△ABC关于y轴对称的△A1B1C1,则点C1的坐标是 (5,3) ;
(2)△ABC的面积是多少?
解:(1)如图,△A1B1C1为所作;则点C1的坐标是(5,3);
故答案为(5,3);
(2)△ABC的面积=2×3﹣×1×2﹣×3×1﹣×1×2=2.5.
23.(8分)如图:AC∥EF,AC=EF,AE=BD.求证:△ABC≌△EDF.
【解答】证明:∵AC∥EF,
∴∠CAB=∠FED,
∵AE=BD,
∴AE+EB=BD+EB,
即AB=ED,
又∵AC=EF,
∴△ABC≌△EDF.
24.(8分)复习“全等三角形”的知识时,老师布置了一道作业题:
“如图①,已知,在△ABC中,AB=AC,P是△ABC中内任意一点,将AP绕点A顺时针旋转至AQ,使∠QAP=∠BAC,连结BQ、CP则BQ=CP.”
小亮是个爱动脑筋的同学,他通过对图①的分析,证明了△ABQ≌△ACP,从而证得BQ=CP.之后,他将点P移到等腰三角形ABC外,原题中其它条件不变,发现“BQ=CP”仍然成立,请你就图②给出证明.
【解答】证明:∵∠QAP=∠BAC
∴∠QAP+∠PAB=∠PAB+∠BAC
即∠QAB=∠PAC
在△ABQ和△ACP中,
,
∴△ABQ≌△ACP(SAS),
∴BQ=CP.
25.(8分)如图,在△ABC中,AB=AC,点D在边AC上,且BD=DA=BC.
(1)如图1,求∠A的度数;
(2)如图2,若M为线段AD上的点,过点M作直线MH⊥BD于点H,分别交直线AB,BC于点N,E.
①求证:△BNE是等腰三角形;
②试写出线段AN,CE,CD之间的数量关系,并加以证明.
解:(1)∵BD=BC,
∴∠BDC=∠C,
∵AB=AC,
∴∠ABC=∠C,
∴∠A=∠DBC,
∵AD=BD,
∴∠A=∠DBA,
∴∠A=∠DBA=∠DBC=∠ABC=∠C,
∵∠A+∠ABC+∠C=5∠A=180°,
∴∠A=36°;
(2)①∵∠A=∠ABD=36°,
∠B=∠C=72°,
∴∠ABD=∠CBD=36°,
∵BH⊥EN,
∴∠BHN=∠EHB=90°,
在△BNH与△BEH中,
,
∴△BNH≌△BEH,
∴BN=BE,
∴△BNE是等腰三角形;
②CD=AN+CE,
理由:由①知,BN=BE,
∵AB=AC,
∴AN=AB﹣BN=AC﹣BE,
∵CE=BE﹣BC,
∵CD=AC﹣AD=AC﹣BD=AC﹣BC,
∴CD=AN+CE.
同课章节目录
