2020-2021学年上海市黄浦区格致初级中学八年级上学期期中数学试卷(Word版 含解析)
文档属性
| 名称 | 2020-2021学年上海市黄浦区格致初级中学八年级上学期期中数学试卷(Word版 含解析) |  | |
| 格式 | doc | ||
| 文件大小 | 702.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-12-25 05:36:22 | ||
图片预览



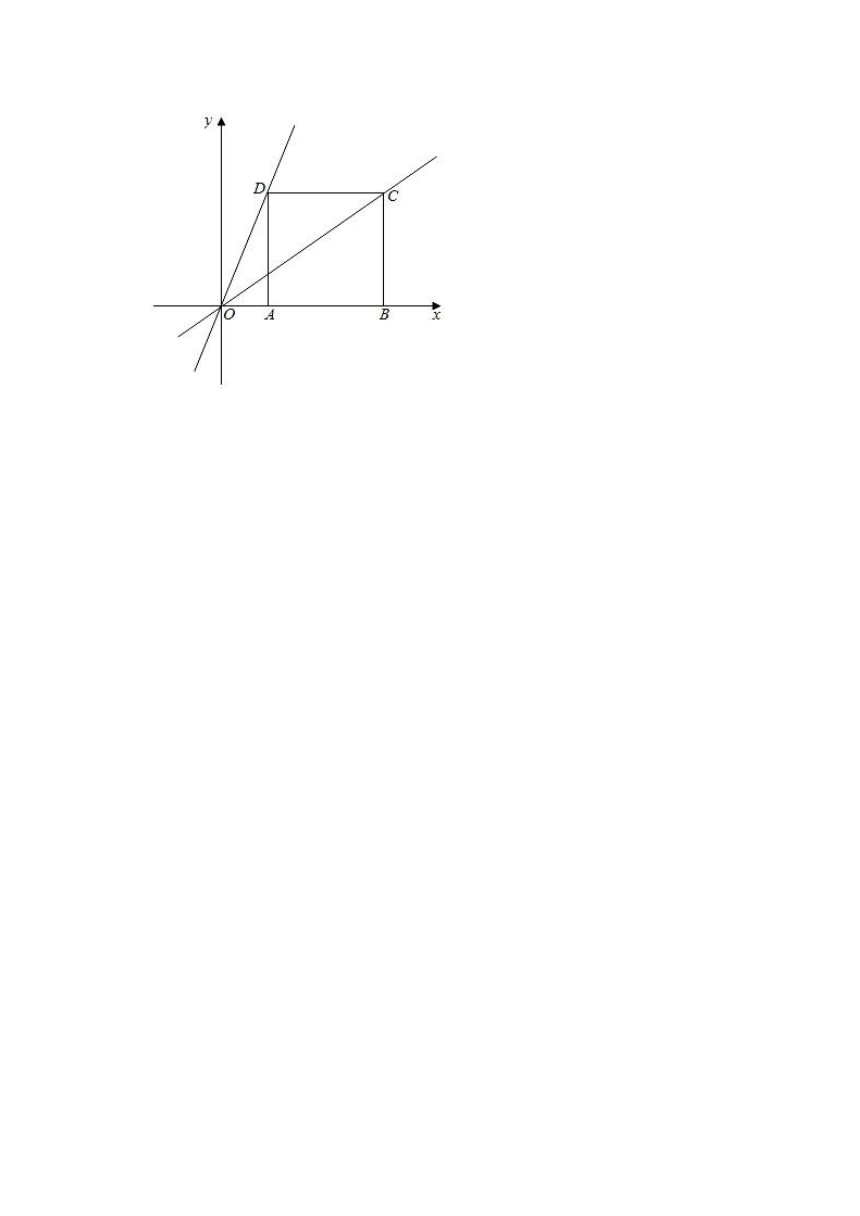

文档简介
2020-2021学年上海市黄浦区格致初级中学八年级第一学期期中数学试卷
一、选择题
1.(2分)下列二次根式中,与是同类二次根式的是( )
A. B. C. D.
2.(2分)下列计算正确的是( )
A. B.
C. D.
3.(2分)+的一个有理化因式是( )
A. B. C. D.
4.(2分)下列方程中,无实数解的是( )
A.2x2+7x+4=0 B.2x2+3x=﹣4
C.y2+49=14y D.﹣5x+12=0
5.(2分)点A(﹣1,y1)、点B(1,y2)在直线y=﹣3x上,则( )
A.y1>y2 B.y1=y2
C.y1<y2 D.无法比较y1、y2大小
6.(2分)已知正比例函数y=(k+1)x与y=(2﹣k)x,则它们图象的大致位置不可能的是( )
A.
B.
C.
D.
二.填空题(本大题共12题,每题2分,满分24分)
7.(2分)化简:= .
8.(2分)化简:= .
9.(2分)如果最简二次根式与是同类二次根式,则a= .
10.(2分)不等式x>x+1的解集是 .
11.(2分)函数的定义域是 .
12.(2分)已知函数f(x)=,则f()= .
13.(2分)方程x2=2x的根为 .
14.(2分)在实数范围内因式分解:x2﹣4x﹣3= .
15.(2分)若一元二次方程ax2﹣bx﹣2016=0有一根为x=﹣1,则a+b= .
16.(2分)关于x的一元二次方程mx2﹣2x+1=0有两个实数根,则m的取值范围是 .
17.(2分)某校八年级举行足球比赛,每个班级都要和其他班级比赛一次,结果一共进行了6场比赛,则八年级共有 个班级.
18.(2分)平面直角坐标系中,点A坐标为(2,2),将点A沿x轴向左平移m个单位后恰好落在正比例函数y=﹣2x的图象上,则m的值为 .
三、简答题:(本大题共6题,每题6分,满分36分)
19.(6分)计算:++2﹣﹣.
20.(6分)计算:×﹣(+).
21.(6分)解方程:(x﹣3)2+4x(x﹣3)=0.
22.(6分)用配方法解方程:x2+2x=4.
23.(6分)已知点(2,﹣4)在正比例函数y=kx的图象上.
(1)求k的值;
(2)若点(﹣1,m)也在此函数y=kx的图象上,试求m的值.
24.(6分)先化简,再求值:﹣.其中a=.
四、解答题:(本大题共3题,25、26题每题8分、27题12分,满分28分)
25.(8分)如图,利用长20米的一段围墙,用篱笆围一个长方形的场地,中间用篱笆分割出2个小长方形,与墙平行的一边上各开一扇宽为1米的门,总共用去篱笆34米,为了使这个长方形ABCD的面积为96平方米,求AB、BC边各为多少米?
26.(8分)已知:正比例函数y=kx的图象经过点A,点A在第四象限,过A作AH⊥x垂足为H,点A的横坐标为3,S△AOH=3.
(1)求点A坐标及此正比例函数解析式;
(2)在x轴上能否找到一点P使S△AOP=5,若存在,求点P坐标;若不存在,说明理由.
27.(12分)如图,正方形ABCD的顶点A、B落在x轴正半轴上,点C落在正比例函数y=kx(k>0)上,点D落在直线y=2x上,且点D的横坐标为a.
(1)直接写出A、B、C、D各点的坐标(用含a的代数式表示);
(2)求出k的值;
(3)将直线OC绕点O旋转,旋转后的直线将正方形ABCD的面积分成1:3两个部分,求旋转后得到的新直线解析式.
参考答案
一、选择题:(本大题共6题,每题2分,满分12分)
1.(2分)下列二次根式中,与是同类二次根式的是( )
A. B. C. D.
解:=2,=3,=2,,
则与是同类二次根式的是.
故选:C.
2.(2分)下列计算正确的是( )
A. B.
C. D.
解:A、和,不能合并同类项,故错误;
B、+=+,故错误;
C、==1,故错误;
D、+=,故正确.
故选:D.
3.(2分)+的一个有理化因式是( )
A. B. C. D.
解:+的一个有理化因式是﹣,
故选:B.
4.(2分)下列方程中,无实数解的是( )
A.2x2+7x+4=0 B.2x2+3x=﹣4
C.y2+49=14y D.﹣5x+12=0
解:A、∵△=72﹣4×2×4=17>0,
∴该方程有两个不相等的实数根;
B、方程可变形为2x2+3x+4=0,
∵△=32﹣4×2×4=﹣23<0,
∴该方程没有实数根;
C、方程可变形为y2﹣14y+49=0,
∵△=(﹣14)2﹣4×1×49=0,
∴该方程有两个相等的实数根;
D、∵△=(﹣5)2﹣4××12=9>0,
∴该方程有两个不相等的实数根.
故选:B.
5.(2分)点A(﹣1,y1)、点B(1,y2)在直线y=﹣3x上,则( )
A.y1>y2 B.y1=y2
C.y1<y2 D.无法比较y1、y2大小
解:∵点A(﹣1,y1)、点B(1,y2)在直线y=﹣3x上,
∴y1=﹣3×(﹣1)=3,y2=﹣3×1=﹣3,
∴y1>y2,
故选:A.
6.(2分)已知正比例函数y=(k+1)x与y=(2﹣k)x,则它们图象的大致位置不可能的是( )
A.
B.
C.
D.
解:当k<﹣1时,正比例函数y=(k+1)x的图象过原点、二、四象限,正比例函数y=(2﹣k)x的图象经过原点,一、三象限,B符合;
当﹣1<k<2时,正比例函数y=(k+1)x的图象过原点、一、三象限,正比例函数y=(2﹣k)x的图象经过原点,一、三象限,A符合;
当k>2时,正比例函数y=(k+1)x的图象过原点、一、三象限,正比例函数y=(2﹣k)x的图象经过原点,二、四象限,C符合;
综上,它们图象的大致位置不可能的是D,
故选:D.
二.填空题(本大题共12题,每题2分,满分24分)
7.(2分)化简:= 4 .
解:,
故答案为:4.
8.(2分)化简:= .
解:因为>1,
所以=﹣1
故答案为:﹣1.
9.(2分)如果最简二次根式与是同类二次根式,则a= 5 .
解:∵最简二次根式与是同类二次根式,
∴3a﹣8=17﹣2a,解得:a=5.
故答案为:5.
10.(2分)不等式x>x+1的解集是 x<﹣1﹣ .
解:移项,得:x﹣x>1,
合并同类项,得:(1﹣)x>1,
系数化为1,得:x<﹣1﹣,
故答案为:x<﹣1﹣.
11.(2分)函数的定义域是 x≤3 .
解:依题意,得3﹣x≥0,
解得x≤3.
故答案为:x≤3.
12.(2分)已知函数f(x)=,则f()= 2+ .
解:∵f(x)=,
∴f()===2+,
故答案为:2+.
13.(2分)方程x2=2x的根为 x1=0,x2=2 .
解:x2=2x,
x2﹣2x=0,
x(x﹣2)=0,
x=0,或x﹣2=0,
x1=0,x2=2,
故答案为:x1=0,x2=2.
14.(2分)在实数范围内因式分解:x2﹣4x﹣3= (x﹣2+)(x﹣2﹣) .
解:令x2﹣4x﹣3=0,
解得:x==2±,
则原式=(x﹣2+)(x﹣2﹣),
故答案为:(x﹣2+)(x﹣2﹣).
15.(2分)若一元二次方程ax2﹣bx﹣2016=0有一根为x=﹣1,则a+b= 2016 .
解:把x=﹣1代入一元二次方程ax2﹣bx﹣2016=0得:a+b﹣2016=0,
即a+b=2016.
故答案是:2016.
16.(2分)关于x的一元二次方程mx2﹣2x+1=0有两个实数根,则m的取值范围是 m≤1且m≠0 .
解:∵关于x的一元二次方程mx2﹣2x+l=0有两个实数根,
∴△=b2﹣4ac=(﹣2)2﹣4m=4﹣4m>0,
∴m<1.
又∵mx2﹣2x+l=0是一元二次方程,
∴m≠0,
故m的取值范围是m≤1且m≠0.
故答案为m≤1且m≠0.
17.(2分)某校八年级举行足球比赛,每个班级都要和其他班级比赛一次,结果一共进行了6场比赛,则八年级共有 3 个班级.
解:设共有x个班级参加比赛,
根据题意得:=6,
整理得:x2﹣x﹣6=0,即(x﹣3)(x+2)=0,
解得:x=3或x=﹣2(舍去).
则共有3个班级球队参加比赛.
故答案为:3.
18.(2分)平面直角坐标系中,点A坐标为(2,2),将点A沿x轴向左平移m个单位后恰好落在正比例函数y=﹣2x的图象上,则m的值为 .
解:∵A坐标为(2,2),
∴将点A沿x轴向左平移m个单位后得到的点的坐标是(2﹣m,2),
∵恰好落在正比例函数y=﹣2x的图象上,
∴(2﹣m)×(﹣2)=2,
解得:m=.
故答案为:.
三、简答题:(本大题共6题,每题6分,满分36分)
19.(6分)计算:++2﹣﹣.
解:原式=2++4﹣﹣3
=+.
20.(6分)计算:×﹣(+).
解:原式=×(3+)﹣(2+2)
=×(6+2)﹣(2+2)
=3+2﹣2﹣2
=.
21.(6分)解方程:(x﹣3)2+4x(x﹣3)=0.
解:原式可化为:(x﹣3)(x﹣3+4x)=0
∴x﹣3=0或5x﹣3=0
解得.
22.(6分)用配方法解方程:x2+2x=4.
解:x2+2x=4,
x2+2x+5=4+5,即(x+)2=9,
∴x+=±3,
∴x1=﹣+3,x2=﹣﹣3.
23.(6分)已知点(2,﹣4)在正比例函数y=kx的图象上.
(1)求k的值;
(2)若点(﹣1,m)也在此函数y=kx的图象上,试求m的值.
解:(1)∵点(2,﹣4)在正比例函数y=kx的图象上,
∴﹣4=2k,解得k=﹣2,
∴这个正比例函数的解析式为y=﹣2x;
(2)∵点(﹣1,m)在函数y=﹣2x的图象上,
∴当x=﹣1时,m=﹣2×(﹣1)=2.
24.(6分)先化简,再求值:﹣.其中a=.
解:a==2﹣<1,
原式=﹣
=a﹣1﹣,
=a﹣1+
=2﹣﹣1+2+
=3.
四、解答题:(本大题共3题,25、26题每题8分、27题12分,满分28分)
25.(8分)如图,利用长20米的一段围墙,用篱笆围一个长方形的场地,中间用篱笆分割出2个小长方形,与墙平行的一边上各开一扇宽为1米的门,总共用去篱笆34米,为了使这个长方形ABCD的面积为96平方米,求AB、BC边各为多少米?
解:设AB为x米,则BC为(36﹣3x)米,
x(36﹣3x)=96,
解得:x1=4,x2=8,
当x=4时,
36﹣3x=24>20(不合题意,舍去),
当x=8时,
36﹣3x=12.
答:AB=8米,BC=12米.
26.(8分)已知:正比例函数y=kx的图象经过点A,点A在第四象限,过A作AH⊥x垂足为H,点A的横坐标为3,S△AOH=3.
(1)求点A坐标及此正比例函数解析式;
(2)在x轴上能否找到一点P使S△AOP=5,若存在,求点P坐标;若不存在,说明理由.
解:(1)∵点A的横坐标为3,且△AOH的面积为3,
∴?3?AH=3,解得AH=2,
∴A(3,﹣2),
把A(3,﹣2)代入y=kx得3k=﹣2,解得k=﹣,
∴正比例函数解析式为y=﹣x;
(2)存在.
设P(t,0),
∵△AOP的面积为5,
∴?|t|?2=5,
∴t=5或t=﹣5,
∴P点坐标为(5,0)或(﹣5,0).
27.(12分)如图,正方形ABCD的顶点A、B落在x轴正半轴上,点C落在正比例函数y=kx(k>0)上,点D落在直线y=2x上,且点D的横坐标为a.
(1)直接写出A、B、C、D各点的坐标(用含a的代数式表示);
(2)求出k的值;
(3)将直线OC绕点O旋转,旋转后的直线将正方形ABCD的面积分成1:3两个部分,求旋转后得到的新直线解析式.
解:(1)点D的横坐标为a,则点D(a,2a),
则AB=AD=2a,则点A、B、C的坐标分别为(a,0)、(3a,0)、(3a,2a),
故点A、B、C、D的坐标分别为(a,0)、(3a,0)、(3a,2a)、(a,2a);
(2)将点C的坐标代入y=kx得,2a=3ak,
解得k=;
(3)设AF=m,则点F(a,m),设直线OC旋转后交AD于点F,交CD于点E,
则直线OF的表达式为y=x,
当y=2a时,y=x=2a,解得x=,故点E(,2a),
由题意得:S△DEF=S正方形ABCD=×(2a)2=a2,
即×DE?EF=×(2a﹣m)×(﹣a)=a2,解得m=3a±a,
则函数的表达式为y=x=(3±)x.
一、选择题
1.(2分)下列二次根式中,与是同类二次根式的是( )
A. B. C. D.
2.(2分)下列计算正确的是( )
A. B.
C. D.
3.(2分)+的一个有理化因式是( )
A. B. C. D.
4.(2分)下列方程中,无实数解的是( )
A.2x2+7x+4=0 B.2x2+3x=﹣4
C.y2+49=14y D.﹣5x+12=0
5.(2分)点A(﹣1,y1)、点B(1,y2)在直线y=﹣3x上,则( )
A.y1>y2 B.y1=y2
C.y1<y2 D.无法比较y1、y2大小
6.(2分)已知正比例函数y=(k+1)x与y=(2﹣k)x,则它们图象的大致位置不可能的是( )
A.
B.
C.
D.
二.填空题(本大题共12题,每题2分,满分24分)
7.(2分)化简:= .
8.(2分)化简:= .
9.(2分)如果最简二次根式与是同类二次根式,则a= .
10.(2分)不等式x>x+1的解集是 .
11.(2分)函数的定义域是 .
12.(2分)已知函数f(x)=,则f()= .
13.(2分)方程x2=2x的根为 .
14.(2分)在实数范围内因式分解:x2﹣4x﹣3= .
15.(2分)若一元二次方程ax2﹣bx﹣2016=0有一根为x=﹣1,则a+b= .
16.(2分)关于x的一元二次方程mx2﹣2x+1=0有两个实数根,则m的取值范围是 .
17.(2分)某校八年级举行足球比赛,每个班级都要和其他班级比赛一次,结果一共进行了6场比赛,则八年级共有 个班级.
18.(2分)平面直角坐标系中,点A坐标为(2,2),将点A沿x轴向左平移m个单位后恰好落在正比例函数y=﹣2x的图象上,则m的值为 .
三、简答题:(本大题共6题,每题6分,满分36分)
19.(6分)计算:++2﹣﹣.
20.(6分)计算:×﹣(+).
21.(6分)解方程:(x﹣3)2+4x(x﹣3)=0.
22.(6分)用配方法解方程:x2+2x=4.
23.(6分)已知点(2,﹣4)在正比例函数y=kx的图象上.
(1)求k的值;
(2)若点(﹣1,m)也在此函数y=kx的图象上,试求m的值.
24.(6分)先化简,再求值:﹣.其中a=.
四、解答题:(本大题共3题,25、26题每题8分、27题12分,满分28分)
25.(8分)如图,利用长20米的一段围墙,用篱笆围一个长方形的场地,中间用篱笆分割出2个小长方形,与墙平行的一边上各开一扇宽为1米的门,总共用去篱笆34米,为了使这个长方形ABCD的面积为96平方米,求AB、BC边各为多少米?
26.(8分)已知:正比例函数y=kx的图象经过点A,点A在第四象限,过A作AH⊥x垂足为H,点A的横坐标为3,S△AOH=3.
(1)求点A坐标及此正比例函数解析式;
(2)在x轴上能否找到一点P使S△AOP=5,若存在,求点P坐标;若不存在,说明理由.
27.(12分)如图,正方形ABCD的顶点A、B落在x轴正半轴上,点C落在正比例函数y=kx(k>0)上,点D落在直线y=2x上,且点D的横坐标为a.
(1)直接写出A、B、C、D各点的坐标(用含a的代数式表示);
(2)求出k的值;
(3)将直线OC绕点O旋转,旋转后的直线将正方形ABCD的面积分成1:3两个部分,求旋转后得到的新直线解析式.
参考答案
一、选择题:(本大题共6题,每题2分,满分12分)
1.(2分)下列二次根式中,与是同类二次根式的是( )
A. B. C. D.
解:=2,=3,=2,,
则与是同类二次根式的是.
故选:C.
2.(2分)下列计算正确的是( )
A. B.
C. D.
解:A、和,不能合并同类项,故错误;
B、+=+,故错误;
C、==1,故错误;
D、+=,故正确.
故选:D.
3.(2分)+的一个有理化因式是( )
A. B. C. D.
解:+的一个有理化因式是﹣,
故选:B.
4.(2分)下列方程中,无实数解的是( )
A.2x2+7x+4=0 B.2x2+3x=﹣4
C.y2+49=14y D.﹣5x+12=0
解:A、∵△=72﹣4×2×4=17>0,
∴该方程有两个不相等的实数根;
B、方程可变形为2x2+3x+4=0,
∵△=32﹣4×2×4=﹣23<0,
∴该方程没有实数根;
C、方程可变形为y2﹣14y+49=0,
∵△=(﹣14)2﹣4×1×49=0,
∴该方程有两个相等的实数根;
D、∵△=(﹣5)2﹣4××12=9>0,
∴该方程有两个不相等的实数根.
故选:B.
5.(2分)点A(﹣1,y1)、点B(1,y2)在直线y=﹣3x上,则( )
A.y1>y2 B.y1=y2
C.y1<y2 D.无法比较y1、y2大小
解:∵点A(﹣1,y1)、点B(1,y2)在直线y=﹣3x上,
∴y1=﹣3×(﹣1)=3,y2=﹣3×1=﹣3,
∴y1>y2,
故选:A.
6.(2分)已知正比例函数y=(k+1)x与y=(2﹣k)x,则它们图象的大致位置不可能的是( )
A.
B.
C.
D.
解:当k<﹣1时,正比例函数y=(k+1)x的图象过原点、二、四象限,正比例函数y=(2﹣k)x的图象经过原点,一、三象限,B符合;
当﹣1<k<2时,正比例函数y=(k+1)x的图象过原点、一、三象限,正比例函数y=(2﹣k)x的图象经过原点,一、三象限,A符合;
当k>2时,正比例函数y=(k+1)x的图象过原点、一、三象限,正比例函数y=(2﹣k)x的图象经过原点,二、四象限,C符合;
综上,它们图象的大致位置不可能的是D,
故选:D.
二.填空题(本大题共12题,每题2分,满分24分)
7.(2分)化简:= 4 .
解:,
故答案为:4.
8.(2分)化简:= .
解:因为>1,
所以=﹣1
故答案为:﹣1.
9.(2分)如果最简二次根式与是同类二次根式,则a= 5 .
解:∵最简二次根式与是同类二次根式,
∴3a﹣8=17﹣2a,解得:a=5.
故答案为:5.
10.(2分)不等式x>x+1的解集是 x<﹣1﹣ .
解:移项,得:x﹣x>1,
合并同类项,得:(1﹣)x>1,
系数化为1,得:x<﹣1﹣,
故答案为:x<﹣1﹣.
11.(2分)函数的定义域是 x≤3 .
解:依题意,得3﹣x≥0,
解得x≤3.
故答案为:x≤3.
12.(2分)已知函数f(x)=,则f()= 2+ .
解:∵f(x)=,
∴f()===2+,
故答案为:2+.
13.(2分)方程x2=2x的根为 x1=0,x2=2 .
解:x2=2x,
x2﹣2x=0,
x(x﹣2)=0,
x=0,或x﹣2=0,
x1=0,x2=2,
故答案为:x1=0,x2=2.
14.(2分)在实数范围内因式分解:x2﹣4x﹣3= (x﹣2+)(x﹣2﹣) .
解:令x2﹣4x﹣3=0,
解得:x==2±,
则原式=(x﹣2+)(x﹣2﹣),
故答案为:(x﹣2+)(x﹣2﹣).
15.(2分)若一元二次方程ax2﹣bx﹣2016=0有一根为x=﹣1,则a+b= 2016 .
解:把x=﹣1代入一元二次方程ax2﹣bx﹣2016=0得:a+b﹣2016=0,
即a+b=2016.
故答案是:2016.
16.(2分)关于x的一元二次方程mx2﹣2x+1=0有两个实数根,则m的取值范围是 m≤1且m≠0 .
解:∵关于x的一元二次方程mx2﹣2x+l=0有两个实数根,
∴△=b2﹣4ac=(﹣2)2﹣4m=4﹣4m>0,
∴m<1.
又∵mx2﹣2x+l=0是一元二次方程,
∴m≠0,
故m的取值范围是m≤1且m≠0.
故答案为m≤1且m≠0.
17.(2分)某校八年级举行足球比赛,每个班级都要和其他班级比赛一次,结果一共进行了6场比赛,则八年级共有 3 个班级.
解:设共有x个班级参加比赛,
根据题意得:=6,
整理得:x2﹣x﹣6=0,即(x﹣3)(x+2)=0,
解得:x=3或x=﹣2(舍去).
则共有3个班级球队参加比赛.
故答案为:3.
18.(2分)平面直角坐标系中,点A坐标为(2,2),将点A沿x轴向左平移m个单位后恰好落在正比例函数y=﹣2x的图象上,则m的值为 .
解:∵A坐标为(2,2),
∴将点A沿x轴向左平移m个单位后得到的点的坐标是(2﹣m,2),
∵恰好落在正比例函数y=﹣2x的图象上,
∴(2﹣m)×(﹣2)=2,
解得:m=.
故答案为:.
三、简答题:(本大题共6题,每题6分,满分36分)
19.(6分)计算:++2﹣﹣.
解:原式=2++4﹣﹣3
=+.
20.(6分)计算:×﹣(+).
解:原式=×(3+)﹣(2+2)
=×(6+2)﹣(2+2)
=3+2﹣2﹣2
=.
21.(6分)解方程:(x﹣3)2+4x(x﹣3)=0.
解:原式可化为:(x﹣3)(x﹣3+4x)=0
∴x﹣3=0或5x﹣3=0
解得.
22.(6分)用配方法解方程:x2+2x=4.
解:x2+2x=4,
x2+2x+5=4+5,即(x+)2=9,
∴x+=±3,
∴x1=﹣+3,x2=﹣﹣3.
23.(6分)已知点(2,﹣4)在正比例函数y=kx的图象上.
(1)求k的值;
(2)若点(﹣1,m)也在此函数y=kx的图象上,试求m的值.
解:(1)∵点(2,﹣4)在正比例函数y=kx的图象上,
∴﹣4=2k,解得k=﹣2,
∴这个正比例函数的解析式为y=﹣2x;
(2)∵点(﹣1,m)在函数y=﹣2x的图象上,
∴当x=﹣1时,m=﹣2×(﹣1)=2.
24.(6分)先化简,再求值:﹣.其中a=.
解:a==2﹣<1,
原式=﹣
=a﹣1﹣,
=a﹣1+
=2﹣﹣1+2+
=3.
四、解答题:(本大题共3题,25、26题每题8分、27题12分,满分28分)
25.(8分)如图,利用长20米的一段围墙,用篱笆围一个长方形的场地,中间用篱笆分割出2个小长方形,与墙平行的一边上各开一扇宽为1米的门,总共用去篱笆34米,为了使这个长方形ABCD的面积为96平方米,求AB、BC边各为多少米?
解:设AB为x米,则BC为(36﹣3x)米,
x(36﹣3x)=96,
解得:x1=4,x2=8,
当x=4时,
36﹣3x=24>20(不合题意,舍去),
当x=8时,
36﹣3x=12.
答:AB=8米,BC=12米.
26.(8分)已知:正比例函数y=kx的图象经过点A,点A在第四象限,过A作AH⊥x垂足为H,点A的横坐标为3,S△AOH=3.
(1)求点A坐标及此正比例函数解析式;
(2)在x轴上能否找到一点P使S△AOP=5,若存在,求点P坐标;若不存在,说明理由.
解:(1)∵点A的横坐标为3,且△AOH的面积为3,
∴?3?AH=3,解得AH=2,
∴A(3,﹣2),
把A(3,﹣2)代入y=kx得3k=﹣2,解得k=﹣,
∴正比例函数解析式为y=﹣x;
(2)存在.
设P(t,0),
∵△AOP的面积为5,
∴?|t|?2=5,
∴t=5或t=﹣5,
∴P点坐标为(5,0)或(﹣5,0).
27.(12分)如图,正方形ABCD的顶点A、B落在x轴正半轴上,点C落在正比例函数y=kx(k>0)上,点D落在直线y=2x上,且点D的横坐标为a.
(1)直接写出A、B、C、D各点的坐标(用含a的代数式表示);
(2)求出k的值;
(3)将直线OC绕点O旋转,旋转后的直线将正方形ABCD的面积分成1:3两个部分,求旋转后得到的新直线解析式.
解:(1)点D的横坐标为a,则点D(a,2a),
则AB=AD=2a,则点A、B、C的坐标分别为(a,0)、(3a,0)、(3a,2a),
故点A、B、C、D的坐标分别为(a,0)、(3a,0)、(3a,2a)、(a,2a);
(2)将点C的坐标代入y=kx得,2a=3ak,
解得k=;
(3)设AF=m,则点F(a,m),设直线OC旋转后交AD于点F,交CD于点E,
则直线OF的表达式为y=x,
当y=2a时,y=x=2a,解得x=,故点E(,2a),
由题意得:S△DEF=S正方形ABCD=×(2a)2=a2,
即×DE?EF=×(2a﹣m)×(﹣a)=a2,解得m=3a±a,
则函数的表达式为y=x=(3±)x.
同课章节目录
