安徽2020-2021学年九年级上第三次(12月份)大联考数学试卷(word版,含解析)
文档属性
| 名称 | 安徽2020-2021学年九年级上第三次(12月份)大联考数学试卷(word版,含解析) |  | |
| 格式 | zip | ||
| 文件大小 | 877.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-12-25 09:02:01 | ||
图片预览




文档简介
安徽2020-2021九年级上第三次(12月份)大联考数学试卷(原卷)
一、选择题(本大题共10小题,每小题4分,满分40分)
1、cos30°的值是(
)
A
B
C
D
2、下列各点中,在反比例函数y=的图象上的是(
)
A
(-1,-4)
B
(-1,4)
C
(-2,2)
D
(2,-2)
3、如图,已知∠DAB=∠CAE,添加下列条件后,仍然无法判定△ABC∽△ADE的是(
)
A.∠B=∠D
B.∠C=∠AED
C
D
第3题
第4题
第6题
第7题
第8题
4、如图,利用标杆BE测量建筑物的高度,A、B、C三点共线,A、E、D三点共线。已知标杆BE高1.8m,测得
AB=2.4m,BC=9.6m,则建筑物CD的高为(
)
A.
6
m
B.
7.2
m
C.
9
m
D.
4
m
5、在Rt△ABC中,∠C=90°,tanA=,则sinB的值为(
)
A
B
C
D
6、如图,在山坡上种树,坡度i=1:2,AB=5m,则相邻两树的水平距离AC为(
)
A.
m
B.
2
m
C.
2
m
D.
4
m
7、如图,在矩形ABCD中,E为AD边上的点,AE=2DE,连接BE交AC于点F,若△AEF的面积为2,则△BCF的面
积为(
)
A.
3
B.
6
C
D.
9
8、如图,在四边形ABCD中,∠B=∠D=90°,若AB=3,BC=2,cosA=,则CD的长为(
)
A
B
2
C
D
9、已知二次函数y=x2+(a+2)x+a(a为常数)的图象的顶点为P(m,n),下列说法正确的是(
)
A.
点P可以在任意一个象限内;
B.
点P只能在第四象限;
C.
n可以等于-2;
D.
n可以等于-
10、如图,已知A、B是反比例函数y=(k>0,x>0)的图象上的两点,BC//y轴,交x轴于点C,动点P从坐标原
点O出发,沿O→A→B→C匀速运动,终点为C,过点P作PQ⊥x轴于点Q,设△OPQ的面积为S,点P运动的时间
为t,则S关于t的函数图象大致为(
)
A
B
C
D
二、填空题(本大题共4小题,每小题5分,满分20分)
11、某公司今年10月份的产值是1000万元,如果该公司第四季度每个月产值的增长率相同,都为x(x>0),今年12月份的产值为y万元,那么y关于x的函数表达式是_
12、已知△ABC与△A1B1C1是关于原点为位似中心的位似图形,且A(2,1),△ABC与△A1B1C1的相似比为,则点A的对应点A1的坐标是_
13、如图,一块含有30°的直角三角板的直角顶点和坐标原点0重合,30°角的顶点A在反比例函数y=的图象上,顶点B在反比例函数y=的图象上,则k的值为
第13题
第14题
14、如图,已知等腰Rt△ABC,AC=BC,D为AB的中点,将点B折叠在边AC上(不与点A、C重合),折痕为EF,点B在边AC上的对应点为M,设CD与EM交于点P,连接PF
(1)△PFM的形状是
;(2)设△PFM的周长为y,若AC=2,则y的取值范围是_
三、(本大题共2小题,每小题8分,满分16分)
15、计算:tan
45°-|-3|-(-)-1
16、已知抛物线y=x2-x-1与x轴的一个交点为(m,0),求代数式-2m2+2m+2021的值
四、(本大题共2小题,每小题8分,满分16分)
17、在由边长为1个单位长度的小正方形组成的网格中,给出了以格点(网格线的交点)为顶点的四边形PABC。
(1)在给定的网格中,以点P为位似中心,将四边形PABC放大为原来的2倍,放大后点A、B、C的对应点分别为A'、B'、C',画出四边形PA'B'C'。
(2)填空:tan∠BCP的值为
18、如图,在△ABC中,DE//BC,AF⊥BC,∠ADE=30°,BF=3.
(1)求AB的长;
(2)若2DE=BC,求DF的长。
五、(本大题共2小题,每小题10分,满分20分)
19、已知反比例函数y=的图象经过点A(2,-4).
(1)求k的值;
(2)若点B(m,6)在这个反比例函数的图象上,则m的值为
(3)点A(x1,y1)、B(x2,y2)均在反比例函数y=的图象上,若x1<
x2,比较y1、y2的大小关系。
20、小华和同学们想用一些测量工具和所学的几何知识测量学校旗杆的高度PA,以检验自己掌握知识和运用知识的能力。如图,旗杆直立于旗台上的点P处,他们的测量方法如下:在阳光下,小华站在旗杆影子的顶端F处。此时,量得小华的影长FG=2m小华的身高EF=1.6
m;同时,在旗杆影子上的点D处,安装测角器CD。测得旗杆顶端A的仰角为49°,量得CD=0.6m,DF=5m,旗台高BP=1.2m。已知在测量过程中,点B、D、F、G在同一水平直线上,点A、P、B在同一条直线上,AB、CD、EF均垂直于BG,设BD=xm
(1)填空:AB的长为_
m(用含x的代数式表示)
(2)求x的值及旗杆的高度PA(参考数据:sin
49°≈0.8,cos49°≈0.7,tan
49°≈1.2)
六、(本题满分12分)
21、如图1,在△ABC中,AB=AC,D为BC边上的动点(点D不与点B、C重合)。以D为顶点作∠ADE=∠B,射线DE
交AC边于点E
(1)求证:△ABD∽△DCE;
(2)若AB=15,tanB=;
①求BC的长;
②如图2,当DE//AB时,过点A作AF⊥AD交射线DE于点F,连接CF,求AE的长
七、(本题满分12分)
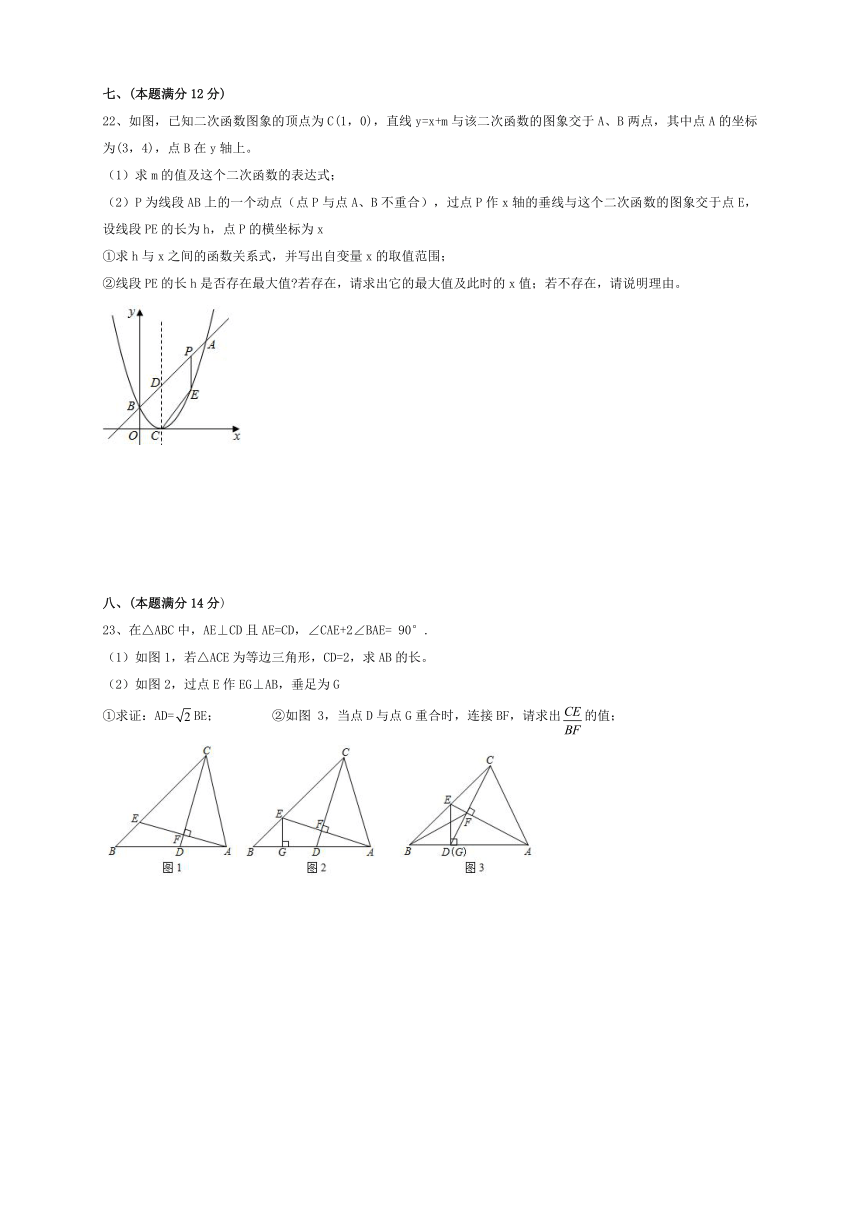
22、如图,已知二次函数图象的顶点为C(1,0),直线y=x+m与该二次函数的图象交于A、B两点,其中点A的坐标为(3,4),点B在y轴上。
(1)求m的值及这个二次函数的表达式;
(2)P为线段AB上的一个动点(点P与点A、B不重合),过点P作x轴的垂线与这个二次函数的图象交于点E,设线段PE的长为h,点P的横坐标为x
①求h与x之间的函数关系式,并写出自变量x的取值范围;
②线段PE的长h是否存在最大值?若存在,请求出它的最大值及此时的x值;若不存在,请说明理由。
八、(本题满分14分)
23、在△ABC中,AE⊥CD且AE=CD,∠CAE+2∠BAE=
90°.
(1)如图1,若△ACE为等边三角形,CD=2,求AB的长。
(2)如图2,过点E作EG⊥AB,垂足为G
①求证:AD=BE;
②如图
3,当点D与点G重合时,连接BF,请求出的值;
安徽2020-2021九年级上第三次(12月份)大联考数学试卷答案及解析
一、选择题(本大题共10小题,每小题4分,满分40分)
1、cos30°的值是(
)
A
B
C
D
【答案】C
【解析】利用特殊角的三角函数的值可知:cos30°=
故选
C
2、下列各点中,在反比例函数y=的图象上的是(
)
A
(-1,-4)
B
(-1,4)
C
(-2,2)
D
(2,-2)
【答案】A
【解析】A、∵-1×(-4)=4,∴该点在函数图象上,故本选项正确符合题意;
B、∵-×4=-4≠4,∴该点不在函数图象上,故本选项不合题意;
C、∵-2×2=-4≠4,∴该点不在函数图象上,故本选项不合题意;
D、2×(-2)=-4≠4,,∴该点不在函数图象上,故本选项不合题意;
故选:A.
3、如图,已知∠DAB=∠CAE,添加下列条件后,仍然无法判定△ABC∽△ADE的是(
)
A.∠B=∠D
B.∠C=∠AED
C
D
【答案】D
【解析】∵∠DAB=∠CAE,∴∠DAE=∠BAC,
A、若∠B=∠D,且∠DAE=∠BAC,可判定△ABC∽△ADE,故选项A不符合题意;
B、若∠C=∠AED,且∠DAE=∠BAC,可判定△ABC∽△ADE,故选项B不符合题意;
C、若,且∠DAE=∠BAC,可判定△ABC∽△ADE,故选项C不符合题意;
D、若,且∠DAE=∠BAC,无法判定△ABC∽△ADE,故选项D符合题意;
故选:D.
4、如图,利用标杆BE测量建筑物的高度,A、B、C三点共线,A、E、D三点共线。已知标杆BE高1.8m,测得
AB=2.4m,BC=9.6m,则建筑物CD的高为(
)
A.
6
m
B.
7.2
m
C.
9
m
D.
4
m
【答案】C
【解析】∵EB∥CD,∴△ABE∽△ACD,∴AB:AC=BE:CD,2.4:(2.4+9.6)=1.8:CD,∴CD=9(米).
故选:C.
5、在Rt△ABC中,∠C=90°,tanA=,则sinB的值为(
)
A
B
C
D
【答案】
【解析】如图所示:∵∠C=90°,tanA=,∴,设BC=12x,AC=5x,故AB=13x,则sinB=.
故选:A.
6、如图,在山坡上种树,坡度i=1:2,AB=5m,则相邻两树的水平距离AC为(
)
A.
m
B.
2
m
C.
2
m
D.
4
m
【答案】B
【解析】∵在山坡上种树,坡度i=1:2,∴设BC=x,则AC=2x,∴x2+(2x)2=52,解得:x=(负值舍去),
故AC=2x=2(m).
故选:B.
7、如图,在矩形ABCD中,E为AD边上的点,AE=2DE,连接BE交AC于点F,若△AEF的面积为2,则△BCF的面
积为(
)
A.
3
B.
6
C
D.
9
【答案】C
【解析】∵AE∥BC,∴△AEF∽△CBF,∴,∵四边形ABCD是矩形,∴AD=BC,∵AE=2DE,
∴,∴4,∴S△BCF=,
故选
C.
8、如图,在四边形ABCD中,∠B=∠D=90°,若AB=3,BC=2,cosA=,则CD的长为(
)
A
B
2
C
D
【答案】D
【解析】延长AD和BC交于点E.∵在直角△ABE中,cosA=,AB=3,∴AE=5,BE=4,∴EC=BE-BC=4-2=2,
∵△ABE和△CDE中,∠B=∠EDC=90°,∠E=∠E,∴∠DCE=∠A,∴直角△CDE中,cos∠DCE
=,
∴设CD=3x,则CE=5x=2,解得:x=,则CD=.
故选
D.
9、已知二次函数y=x2+(a+2)x+a(a为常数)的图象的顶点为P(m,n),下列说法正确的是(
)
A.
点P可以在任意一个象限内;
B.
点P只能在第四象限;
C.
n可以等于-2;
D.
n可以等于-
【答案】C
【解析】二次函数y=
x2+(a+2)x+a(a为常数)的图象顶点P(m,n),∴m=,n=,∵a2≥0,∴a2+4≥4,∴n=≤?1,
故选:C.
10、如图,已知A、B是反比例函数y=(k>0,x>0)的图象上的两点,BC//y轴,交x轴于点C,动点P从坐标原
点O出发,沿O→A→B→C匀速运动,终点为C,过点P作PQ⊥x轴于点Q,设△OPQ的面积为S,点P运动的时间
为t,则S关于t的函数图象大致为(
)
A
B
C
D
【答案】B
【解析】①当点P在线段OA上运动时.设P(x,y).则S=ax2(a是大于0的常数,x>0),图象为抛物线的一部分,排除C;
②当点P在AB上运动时,此时△OPQ的面积S=k(k>0),保持不变,排除D;
③点P在BC上运动时,设路线O→A→B→C的总路程为l,点P的速度为b,则S=OC×BC=OC×(l-at),
因为l,OC,a均是常数,所以S与t成一次函数关系.故排除A.
故选:B.
二、填空题(本大题共4小题,每小题5分,满分20分)
11、某公司今年10月份的产值是1000万元,如果该公司第四季度每个月产值的增长率相同,都为x(x>0),今年12月份的产值为y万元,那么y关于x的函数表达式是_
【答案】y=100(1+x)2
【解析】由题意可得,y=100(1+x)2,
故答案为:y=100(1+x)2.
12、已知△ABC与△A1B1C1是关于原点为位似中心的位似图形,且A(2,1),△ABC与△A1B1C1的相似比为,则点A的对应点A1的坐标是_
【答案】(8,4)或(-8,-4)
【解析】△ABC与△A1B1C1是关于原点为中心的位似图形,A(2,1),△ABC与△A1B1C1的相似比为,
∴A的对应点A1的坐标是(2×4,1×4)或(-2×4,-1×4),即(8,4)或(-8,-4),
故答案为:(8,4)或(-8,-4).
13、如图,一块含有30°的直角三角板的直角顶点和坐标原点0重合,30°角的顶点A在反比例函数y=的图象上,顶点B在反比例函数y=的图象上,则k的值为
【答案】-18
【解析】过点A、B分别作x轴的垂线,垂足分别为C、D,在Rt△ABO中,∠BAO=30°,∠AOB=90°,
∴=tan30°=,∵∠BOD+∠OBD=90°,∠BOD+∠AOC=180°-90°=90°,∴∠OBD=∠AOC,
又∵∠ACO=∠ODB=90°,∴△AOC∽△OBD,∴,∵点B在y=的图象上,∴S△OBD=|6|=3,
∴S△AOC=3S△OBD=3×3=9=|k|,∴k=±18,又∵点A在第二象限,∴k=-18,
故答案为-18.
14、如图,已知等腰Rt△ABC,AC=BC,D为AB的中点,将点B折叠在边AC上(不与点A、C重合),折痕为EF,点B在边AC上的对应点为M,设CD与EM交于点P,连接PF
(1)△PFM的形状是
;(2)设△PFM的周长为y,若AC=2,则y的取值范围是_
【答案】
【解析】(1)△PFM的形状是等腰直角三角形,不会发生变化,理由如下:由折叠的性质可知,∠PMF=∠B=45°,∵CD是中垂线,∴∠ACD=∠DCF=45°,∴∠PMO=∠FCO,∵∠POM=∠FOC,∴△POM∽△FOC,∴,
∴,∵∠POF=∠MOC,∴△POF∽△MOC,∴∠PFO=∠MCO=45°,∴∠PFM=∠PMF=45°,∴∠MPF=90°,∴△PFM是等腰直角三角形.
(2)∵△PFM是等腰直角三角形,设FM=x,由勾股定理可知:PF=PM=,∴△PFM的周长y=(1+)x,
∵1<x<2,∴△PFM的周长满足:1+<y<2+2.
三、(本大题共2小题,每小题8分,满分16分)
15、计算:tan
45°-|-3|-(-)-1
【答案】
【解析】原式=1-3-(-2)=1-3+2=0
16、已知抛物线y=x2-x-1与x轴的一个交点为(m,0),求代数式-2m2+2m+2021的值
【答案】
【解析】∵抛物线y=x2-x-1与x轴的一个交点为(m,0),∴m2-m-1=0,即m2-m=1
-2m2+2m+2021=-2(m2-m)+2021=-2×1+2021=2019
四、(本大题共2小题,每小题8分,满分16分)
17、在由边长为1个单位长度的小正方形组成的网格中,给出了以格点(网格线的交点)为顶点的四边形PABC。
(1)在给定的网格中,以点P为位似中心,将四边形PABC放大为原来的2倍,放大后点A、B、C的对应点分别为A'、B'、C',画出四边形PA'B'C'。
(2)填空:tan∠BCP的值为
【答案】
【解析】(1)如图所示:;
(2)
连接PB,则PBC=90°,由勾股定理知:BC=;PB=2
,tan∠BCP=;
18、如图,在△ABC中,DE//BC,AF⊥BC,∠ADE=30°,BF=3.
(1)求AB的长;
(2)若2DE=BC,求DF的长。
【答案】
【解析】(1)∵DE∥BC,∴∠B=∠ADE=30°,∵AF⊥BC,∴∠AFB=90°,∴AB=BF/cosB=6;
(2)∵DE∥BC,∴△ADE∽△ABC,∴AD:AB=DE:BC=1:2,∴点D是AB的中点,在Rt△AFB中,
点D是AB的中点,∴DF=AB=3.
五、(本大题共2小题,每小题10分,满分20分)
19、已知反比例函数y=的图象经过点A(2,-4).
(1)求k的值;
(2)若点B(m,6)在这个反比例函数的图象上,则m的值为
(3)点A(x1,y1)、B(x2,y2)均在反比例函数y=的图象上,若x1<
x2,比较y1、y2的大小关系。
【答案】
【解析】(1)依题意得:1-k=2×(-4)=-8,所以k=9;
(2)∵点B(m,6)在这个反比例函数的图象上,6m=-8,∴m=-;
(3)∵点A(x1,y1)、B(x2,y2)都在反比例函数y=-的图象上,-8<0,
所以当A、B同时在第二或第四象限时,即x1<x2<0时或0<x1<x2时,y1<y2;
当A在第二象限,B在第四象限时,即x1<0<x2时,y2<y1;
20、小华和同学们想用一些测量工具和所学的几何知识测量学校旗杆的高度PA,以检验自己掌握知识和运用知识的能力。如图,旗杆直立于旗台上的点P处,他们的测量方法如下:在阳光下,小华站在旗杆影子的顶端F处。此时,量得小华的影长FG=2m小华的身高EF=1.6
m;同时,在旗杆影子上的点D处,安装测角器CD。测得旗杆顶端A的仰角为49°,量得CD=0.6m,DF=5m,旗台高BP=1.2m。已知在测量过程中,点B、D、F、G在同一水平直线上,点A、P、B在同一条直线上,AB、CD、EF均垂直于BG,设BD=xm
(1)填空:AB的长为_
m(用含x的代数式表示)
(2)求x的值及旗杆的高度PA(参考数据:sin
49°≈0.8,cos49°≈0.7,tan
49°≈1.2)
【答案】
【解析】(1)过C作CH⊥AB于H,则四边形BDCH是矩形,∴CH=BD,BH=CD=0.6m,设BD=CH=x,则BF=(5+x)m,在Rt△AHC中,tan∠ACH=AH/CH,∴AH=CH?tan49°=1.2x,∴AB=1.2x+0.6,
(2)连接EG,∵∠ABF=∠EFG=90°,∠AFB=∠EGF,∴△ABF∽△EFG,∴AB:EF=BF:FG,
∴(1.2x+0.6):1.6=(5+x):2,解得:x=8.5,∴AB=10.8,∴AP=10.8-1.2=9.6(m)
答:旗杆的高度PA为9.6m.
六、(本题满分12分)
21、如图1,在△ABC中,AB=AC,D为BC边上的动点(点D不与点B、C重合)。以D为顶点作∠ADE=∠B,射线DE
交AC边于点E
(1)求证:△ABD∽△DCE;
(2)若AB=15,tanB=;
①求BC的长;
②如图2,当DE//AB时,过点A作AF⊥AD交射线DE于点F,连接CF,求AE的长
【答案】
【解析】(1)∵AB=AC,∴∠B=∠ACB,∵∠ADE+∠CDE=∠B+∠BAD,∠ADE=∠B,∴∠BAD=∠CDE,
∴△BAD∽△DCE;
(2)如图2中,作AM⊥BC于M.
在Rt△ABM中,设BM=4k,∵tanB==,∴AM=BM?tanB=4k×=3k,由勾股定理,得到AB2=AM2+BM2,
∴152=(3k)2+(4k)2,∴k=3或-3(舍弃),∴AM=9,BM=12,∵AB=AC,AM⊥BC,∴BC=2BM=2×4k=24,
(3)点D在BC边上运动的过程中,存在某个位置,使得DF=CF.
∵DE∥AB,∴∠BAD=∠ADE,∵∠ADE=∠B,∠B=∠ACB,∴∠BAD=∠ACB,∵∠ABD=∠CBA,∴△ABD∽△CBA,
∴AB:CB=DB:AB,∴DB===,∵DE∥AB,∴AE:AC=BD:BC,∴AE===.
七、(本题满分12分)
22、如图,已知二次函数图象的顶点为C(1,0),直线y=x+m与该二次函数的图象交于A、B两点,其中点A的坐标为(3,4),点B在y轴上。
(1)求m的值及这个二次函数的表达式;
(2)P为线段AB上的一个动点(点P与点A、B不重合),过点P作x轴的垂线与这个二次函数的图象交于点E,设线段PE的长为h,点P的横坐标为x
①求h与x之间的函数关系式,并写出自变量x的取值范围;
②线段PE的长h是否存在最大值?若存在,请求出它的最大值及此时的x值;若不存在,请说明理由。
【答案】
【解析】(1)∵点A(3,4)在直线y=x+m上,∴4=3+m.∴m=1.设所求二次函数的关系式为y=a(x-1)2.
∵点A(3,4)在二次函数y=a(x-1)2的图象上,∴4=a(3-1)2,∴a=1.
∴所求二次函数的关系式为y=(x-1)2.即y=x2-2x+1.
(2)①设P、E两点的纵坐标分别为yP和yE.∴PE=h=yP-yE=(x+1)-(x2-2x+1)=-x2+3x.
即h=-x2+3x(0<x<3).
②存在.∵h=-(x-)2+,又∵a=-1<0,∴x=时,h的值最大,最大值为.
八、(本题满分14分)
23、在△ABC中,AE⊥CD且AE=CD,∠CAE+2∠BAE=
90°.
(1)如图1,若△ACE为等边三角形,CD=2,求AB的长。
(2)如图2,过点E作EG⊥AB,垂足为G
①求证:AD=BE;
②如图3,当点D与点G重合时,连接BF,请求出的值;
【答案】
【解析】(1)∵若△ACE为等边三角形,∴AC=AE=CD=2,且∠CEA=∠CAE=60°,∵∠CAE+2∠BAE=
90°,∴∠BAE=15°,
∠B=45°,过点A作AK⊥BC,垂足为K,则AK=×AC=,且AB=AK=;
(2)①过点C作CM⊥AB,M为垂足,设∠BAE=β,∵∠CAE+2∠BAE=
90°,∴∠CAE=90°-2β,∵AE⊥CD,
∴∠ACD=2β,∵AE⊥CD,∴∠CAE=90°-[90°-2β+β]=
β,∴∠DCM=∠ACM=∠BAE=
β,CM=CM,
∠CMD=∠CMA=90°,∴△AMC≌△DMC,∴AM=DM,且AC=CD=AE,在△AGE与△AMC中,∠ACM=∠BAE,
∠AGE=∠CMA=90°,AC=AE,
∴△AMC≌△EGA,∴AM=EG,
∴EGAD,在等腰△AEC中,∠EAC=90°-β,
∴∠AEC=45°+β,∴∠B=45°,∵EG⊥AB,∴BE=EG=×AD,即AD=BE;
②过点C、F分别作CM⊥AB、FH⊥AB,垂足为M、H,则ED//FH//CM;由①知:AM=MD=BD=DE,设BD=a,AM=DM=DE=a,
AD=2a,由勾股定理得到:BE=a,AE=a;则DF=a,
EF=a,
AF=a,
∵FH//ED,∴△AHF∽△ADE,
∴FH:DE=AF:AE=AH:AD,解得:FH=a;
AH=a;
则BH=a;
由勾股定理:BF=a,;=,
一、选择题(本大题共10小题,每小题4分,满分40分)
1、cos30°的值是(
)
A
B
C
D
2、下列各点中,在反比例函数y=的图象上的是(
)
A
(-1,-4)
B
(-1,4)
C
(-2,2)
D
(2,-2)
3、如图,已知∠DAB=∠CAE,添加下列条件后,仍然无法判定△ABC∽△ADE的是(
)
A.∠B=∠D
B.∠C=∠AED
C
D
第3题
第4题
第6题
第7题
第8题
4、如图,利用标杆BE测量建筑物的高度,A、B、C三点共线,A、E、D三点共线。已知标杆BE高1.8m,测得
AB=2.4m,BC=9.6m,则建筑物CD的高为(
)
A.
6
m
B.
7.2
m
C.
9
m
D.
4
m
5、在Rt△ABC中,∠C=90°,tanA=,则sinB的值为(
)
A
B
C
D
6、如图,在山坡上种树,坡度i=1:2,AB=5m,则相邻两树的水平距离AC为(
)
A.
m
B.
2
m
C.
2
m
D.
4
m
7、如图,在矩形ABCD中,E为AD边上的点,AE=2DE,连接BE交AC于点F,若△AEF的面积为2,则△BCF的面
积为(
)
A.
3
B.
6
C
D.
9
8、如图,在四边形ABCD中,∠B=∠D=90°,若AB=3,BC=2,cosA=,则CD的长为(
)
A
B
2
C
D
9、已知二次函数y=x2+(a+2)x+a(a为常数)的图象的顶点为P(m,n),下列说法正确的是(
)
A.
点P可以在任意一个象限内;
B.
点P只能在第四象限;
C.
n可以等于-2;
D.
n可以等于-
10、如图,已知A、B是反比例函数y=(k>0,x>0)的图象上的两点,BC//y轴,交x轴于点C,动点P从坐标原
点O出发,沿O→A→B→C匀速运动,终点为C,过点P作PQ⊥x轴于点Q,设△OPQ的面积为S,点P运动的时间
为t,则S关于t的函数图象大致为(
)
A
B
C
D
二、填空题(本大题共4小题,每小题5分,满分20分)
11、某公司今年10月份的产值是1000万元,如果该公司第四季度每个月产值的增长率相同,都为x(x>0),今年12月份的产值为y万元,那么y关于x的函数表达式是_
12、已知△ABC与△A1B1C1是关于原点为位似中心的位似图形,且A(2,1),△ABC与△A1B1C1的相似比为,则点A的对应点A1的坐标是_
13、如图,一块含有30°的直角三角板的直角顶点和坐标原点0重合,30°角的顶点A在反比例函数y=的图象上,顶点B在反比例函数y=的图象上,则k的值为
第13题
第14题
14、如图,已知等腰Rt△ABC,AC=BC,D为AB的中点,将点B折叠在边AC上(不与点A、C重合),折痕为EF,点B在边AC上的对应点为M,设CD与EM交于点P,连接PF
(1)△PFM的形状是
;(2)设△PFM的周长为y,若AC=2,则y的取值范围是_
三、(本大题共2小题,每小题8分,满分16分)
15、计算:tan
45°-|-3|-(-)-1
16、已知抛物线y=x2-x-1与x轴的一个交点为(m,0),求代数式-2m2+2m+2021的值
四、(本大题共2小题,每小题8分,满分16分)
17、在由边长为1个单位长度的小正方形组成的网格中,给出了以格点(网格线的交点)为顶点的四边形PABC。
(1)在给定的网格中,以点P为位似中心,将四边形PABC放大为原来的2倍,放大后点A、B、C的对应点分别为A'、B'、C',画出四边形PA'B'C'。
(2)填空:tan∠BCP的值为
18、如图,在△ABC中,DE//BC,AF⊥BC,∠ADE=30°,BF=3.
(1)求AB的长;
(2)若2DE=BC,求DF的长。
五、(本大题共2小题,每小题10分,满分20分)
19、已知反比例函数y=的图象经过点A(2,-4).
(1)求k的值;
(2)若点B(m,6)在这个反比例函数的图象上,则m的值为
(3)点A(x1,y1)、B(x2,y2)均在反比例函数y=的图象上,若x1<
x2,比较y1、y2的大小关系。
20、小华和同学们想用一些测量工具和所学的几何知识测量学校旗杆的高度PA,以检验自己掌握知识和运用知识的能力。如图,旗杆直立于旗台上的点P处,他们的测量方法如下:在阳光下,小华站在旗杆影子的顶端F处。此时,量得小华的影长FG=2m小华的身高EF=1.6
m;同时,在旗杆影子上的点D处,安装测角器CD。测得旗杆顶端A的仰角为49°,量得CD=0.6m,DF=5m,旗台高BP=1.2m。已知在测量过程中,点B、D、F、G在同一水平直线上,点A、P、B在同一条直线上,AB、CD、EF均垂直于BG,设BD=xm
(1)填空:AB的长为_
m(用含x的代数式表示)
(2)求x的值及旗杆的高度PA(参考数据:sin
49°≈0.8,cos49°≈0.7,tan
49°≈1.2)
六、(本题满分12分)
21、如图1,在△ABC中,AB=AC,D为BC边上的动点(点D不与点B、C重合)。以D为顶点作∠ADE=∠B,射线DE
交AC边于点E
(1)求证:△ABD∽△DCE;
(2)若AB=15,tanB=;
①求BC的长;
②如图2,当DE//AB时,过点A作AF⊥AD交射线DE于点F,连接CF,求AE的长
七、(本题满分12分)
22、如图,已知二次函数图象的顶点为C(1,0),直线y=x+m与该二次函数的图象交于A、B两点,其中点A的坐标为(3,4),点B在y轴上。
(1)求m的值及这个二次函数的表达式;
(2)P为线段AB上的一个动点(点P与点A、B不重合),过点P作x轴的垂线与这个二次函数的图象交于点E,设线段PE的长为h,点P的横坐标为x
①求h与x之间的函数关系式,并写出自变量x的取值范围;
②线段PE的长h是否存在最大值?若存在,请求出它的最大值及此时的x值;若不存在,请说明理由。
八、(本题满分14分)
23、在△ABC中,AE⊥CD且AE=CD,∠CAE+2∠BAE=
90°.
(1)如图1,若△ACE为等边三角形,CD=2,求AB的长。
(2)如图2,过点E作EG⊥AB,垂足为G
①求证:AD=BE;
②如图
3,当点D与点G重合时,连接BF,请求出的值;
安徽2020-2021九年级上第三次(12月份)大联考数学试卷答案及解析
一、选择题(本大题共10小题,每小题4分,满分40分)
1、cos30°的值是(
)
A
B
C
D
【答案】C
【解析】利用特殊角的三角函数的值可知:cos30°=
故选
C
2、下列各点中,在反比例函数y=的图象上的是(
)
A
(-1,-4)
B
(-1,4)
C
(-2,2)
D
(2,-2)
【答案】A
【解析】A、∵-1×(-4)=4,∴该点在函数图象上,故本选项正确符合题意;
B、∵-×4=-4≠4,∴该点不在函数图象上,故本选项不合题意;
C、∵-2×2=-4≠4,∴该点不在函数图象上,故本选项不合题意;
D、2×(-2)=-4≠4,,∴该点不在函数图象上,故本选项不合题意;
故选:A.
3、如图,已知∠DAB=∠CAE,添加下列条件后,仍然无法判定△ABC∽△ADE的是(
)
A.∠B=∠D
B.∠C=∠AED
C
D
【答案】D
【解析】∵∠DAB=∠CAE,∴∠DAE=∠BAC,
A、若∠B=∠D,且∠DAE=∠BAC,可判定△ABC∽△ADE,故选项A不符合题意;
B、若∠C=∠AED,且∠DAE=∠BAC,可判定△ABC∽△ADE,故选项B不符合题意;
C、若,且∠DAE=∠BAC,可判定△ABC∽△ADE,故选项C不符合题意;
D、若,且∠DAE=∠BAC,无法判定△ABC∽△ADE,故选项D符合题意;
故选:D.
4、如图,利用标杆BE测量建筑物的高度,A、B、C三点共线,A、E、D三点共线。已知标杆BE高1.8m,测得
AB=2.4m,BC=9.6m,则建筑物CD的高为(
)
A.
6
m
B.
7.2
m
C.
9
m
D.
4
m
【答案】C
【解析】∵EB∥CD,∴△ABE∽△ACD,∴AB:AC=BE:CD,2.4:(2.4+9.6)=1.8:CD,∴CD=9(米).
故选:C.
5、在Rt△ABC中,∠C=90°,tanA=,则sinB的值为(
)
A
B
C
D
【答案】
【解析】如图所示:∵∠C=90°,tanA=,∴,设BC=12x,AC=5x,故AB=13x,则sinB=.
故选:A.
6、如图,在山坡上种树,坡度i=1:2,AB=5m,则相邻两树的水平距离AC为(
)
A.
m
B.
2
m
C.
2
m
D.
4
m
【答案】B
【解析】∵在山坡上种树,坡度i=1:2,∴设BC=x,则AC=2x,∴x2+(2x)2=52,解得:x=(负值舍去),
故AC=2x=2(m).
故选:B.
7、如图,在矩形ABCD中,E为AD边上的点,AE=2DE,连接BE交AC于点F,若△AEF的面积为2,则△BCF的面
积为(
)
A.
3
B.
6
C
D.
9
【答案】C
【解析】∵AE∥BC,∴△AEF∽△CBF,∴,∵四边形ABCD是矩形,∴AD=BC,∵AE=2DE,
∴,∴4,∴S△BCF=,
故选
C.
8、如图,在四边形ABCD中,∠B=∠D=90°,若AB=3,BC=2,cosA=,则CD的长为(
)
A
B
2
C
D
【答案】D
【解析】延长AD和BC交于点E.∵在直角△ABE中,cosA=,AB=3,∴AE=5,BE=4,∴EC=BE-BC=4-2=2,
∵△ABE和△CDE中,∠B=∠EDC=90°,∠E=∠E,∴∠DCE=∠A,∴直角△CDE中,cos∠DCE
=,
∴设CD=3x,则CE=5x=2,解得:x=,则CD=.
故选
D.
9、已知二次函数y=x2+(a+2)x+a(a为常数)的图象的顶点为P(m,n),下列说法正确的是(
)
A.
点P可以在任意一个象限内;
B.
点P只能在第四象限;
C.
n可以等于-2;
D.
n可以等于-
【答案】C
【解析】二次函数y=
x2+(a+2)x+a(a为常数)的图象顶点P(m,n),∴m=,n=,∵a2≥0,∴a2+4≥4,∴n=≤?1,
故选:C.
10、如图,已知A、B是反比例函数y=(k>0,x>0)的图象上的两点,BC//y轴,交x轴于点C,动点P从坐标原
点O出发,沿O→A→B→C匀速运动,终点为C,过点P作PQ⊥x轴于点Q,设△OPQ的面积为S,点P运动的时间
为t,则S关于t的函数图象大致为(
)
A
B
C
D
【答案】B
【解析】①当点P在线段OA上运动时.设P(x,y).则S=ax2(a是大于0的常数,x>0),图象为抛物线的一部分,排除C;
②当点P在AB上运动时,此时△OPQ的面积S=k(k>0),保持不变,排除D;
③点P在BC上运动时,设路线O→A→B→C的总路程为l,点P的速度为b,则S=OC×BC=OC×(l-at),
因为l,OC,a均是常数,所以S与t成一次函数关系.故排除A.
故选:B.
二、填空题(本大题共4小题,每小题5分,满分20分)
11、某公司今年10月份的产值是1000万元,如果该公司第四季度每个月产值的增长率相同,都为x(x>0),今年12月份的产值为y万元,那么y关于x的函数表达式是_
【答案】y=100(1+x)2
【解析】由题意可得,y=100(1+x)2,
故答案为:y=100(1+x)2.
12、已知△ABC与△A1B1C1是关于原点为位似中心的位似图形,且A(2,1),△ABC与△A1B1C1的相似比为,则点A的对应点A1的坐标是_
【答案】(8,4)或(-8,-4)
【解析】△ABC与△A1B1C1是关于原点为中心的位似图形,A(2,1),△ABC与△A1B1C1的相似比为,
∴A的对应点A1的坐标是(2×4,1×4)或(-2×4,-1×4),即(8,4)或(-8,-4),
故答案为:(8,4)或(-8,-4).
13、如图,一块含有30°的直角三角板的直角顶点和坐标原点0重合,30°角的顶点A在反比例函数y=的图象上,顶点B在反比例函数y=的图象上,则k的值为
【答案】-18
【解析】过点A、B分别作x轴的垂线,垂足分别为C、D,在Rt△ABO中,∠BAO=30°,∠AOB=90°,
∴=tan30°=,∵∠BOD+∠OBD=90°,∠BOD+∠AOC=180°-90°=90°,∴∠OBD=∠AOC,
又∵∠ACO=∠ODB=90°,∴△AOC∽△OBD,∴,∵点B在y=的图象上,∴S△OBD=|6|=3,
∴S△AOC=3S△OBD=3×3=9=|k|,∴k=±18,又∵点A在第二象限,∴k=-18,
故答案为-18.
14、如图,已知等腰Rt△ABC,AC=BC,D为AB的中点,将点B折叠在边AC上(不与点A、C重合),折痕为EF,点B在边AC上的对应点为M,设CD与EM交于点P,连接PF
(1)△PFM的形状是
;(2)设△PFM的周长为y,若AC=2,则y的取值范围是_
【答案】
【解析】(1)△PFM的形状是等腰直角三角形,不会发生变化,理由如下:由折叠的性质可知,∠PMF=∠B=45°,∵CD是中垂线,∴∠ACD=∠DCF=45°,∴∠PMO=∠FCO,∵∠POM=∠FOC,∴△POM∽△FOC,∴,
∴,∵∠POF=∠MOC,∴△POF∽△MOC,∴∠PFO=∠MCO=45°,∴∠PFM=∠PMF=45°,∴∠MPF=90°,∴△PFM是等腰直角三角形.
(2)∵△PFM是等腰直角三角形,设FM=x,由勾股定理可知:PF=PM=,∴△PFM的周长y=(1+)x,
∵1<x<2,∴△PFM的周长满足:1+<y<2+2.
三、(本大题共2小题,每小题8分,满分16分)
15、计算:tan
45°-|-3|-(-)-1
【答案】
【解析】原式=1-3-(-2)=1-3+2=0
16、已知抛物线y=x2-x-1与x轴的一个交点为(m,0),求代数式-2m2+2m+2021的值
【答案】
【解析】∵抛物线y=x2-x-1与x轴的一个交点为(m,0),∴m2-m-1=0,即m2-m=1
-2m2+2m+2021=-2(m2-m)+2021=-2×1+2021=2019
四、(本大题共2小题,每小题8分,满分16分)
17、在由边长为1个单位长度的小正方形组成的网格中,给出了以格点(网格线的交点)为顶点的四边形PABC。
(1)在给定的网格中,以点P为位似中心,将四边形PABC放大为原来的2倍,放大后点A、B、C的对应点分别为A'、B'、C',画出四边形PA'B'C'。
(2)填空:tan∠BCP的值为
【答案】
【解析】(1)如图所示:;
(2)
连接PB,则PBC=90°,由勾股定理知:BC=;PB=2
,tan∠BCP=;
18、如图,在△ABC中,DE//BC,AF⊥BC,∠ADE=30°,BF=3.
(1)求AB的长;
(2)若2DE=BC,求DF的长。
【答案】
【解析】(1)∵DE∥BC,∴∠B=∠ADE=30°,∵AF⊥BC,∴∠AFB=90°,∴AB=BF/cosB=6;
(2)∵DE∥BC,∴△ADE∽△ABC,∴AD:AB=DE:BC=1:2,∴点D是AB的中点,在Rt△AFB中,
点D是AB的中点,∴DF=AB=3.
五、(本大题共2小题,每小题10分,满分20分)
19、已知反比例函数y=的图象经过点A(2,-4).
(1)求k的值;
(2)若点B(m,6)在这个反比例函数的图象上,则m的值为
(3)点A(x1,y1)、B(x2,y2)均在反比例函数y=的图象上,若x1<
x2,比较y1、y2的大小关系。
【答案】
【解析】(1)依题意得:1-k=2×(-4)=-8,所以k=9;
(2)∵点B(m,6)在这个反比例函数的图象上,6m=-8,∴m=-;
(3)∵点A(x1,y1)、B(x2,y2)都在反比例函数y=-的图象上,-8<0,
所以当A、B同时在第二或第四象限时,即x1<x2<0时或0<x1<x2时,y1<y2;
当A在第二象限,B在第四象限时,即x1<0<x2时,y2<y1;
20、小华和同学们想用一些测量工具和所学的几何知识测量学校旗杆的高度PA,以检验自己掌握知识和运用知识的能力。如图,旗杆直立于旗台上的点P处,他们的测量方法如下:在阳光下,小华站在旗杆影子的顶端F处。此时,量得小华的影长FG=2m小华的身高EF=1.6
m;同时,在旗杆影子上的点D处,安装测角器CD。测得旗杆顶端A的仰角为49°,量得CD=0.6m,DF=5m,旗台高BP=1.2m。已知在测量过程中,点B、D、F、G在同一水平直线上,点A、P、B在同一条直线上,AB、CD、EF均垂直于BG,设BD=xm
(1)填空:AB的长为_
m(用含x的代数式表示)
(2)求x的值及旗杆的高度PA(参考数据:sin
49°≈0.8,cos49°≈0.7,tan
49°≈1.2)
【答案】
【解析】(1)过C作CH⊥AB于H,则四边形BDCH是矩形,∴CH=BD,BH=CD=0.6m,设BD=CH=x,则BF=(5+x)m,在Rt△AHC中,tan∠ACH=AH/CH,∴AH=CH?tan49°=1.2x,∴AB=1.2x+0.6,
(2)连接EG,∵∠ABF=∠EFG=90°,∠AFB=∠EGF,∴△ABF∽△EFG,∴AB:EF=BF:FG,
∴(1.2x+0.6):1.6=(5+x):2,解得:x=8.5,∴AB=10.8,∴AP=10.8-1.2=9.6(m)
答:旗杆的高度PA为9.6m.
六、(本题满分12分)
21、如图1,在△ABC中,AB=AC,D为BC边上的动点(点D不与点B、C重合)。以D为顶点作∠ADE=∠B,射线DE
交AC边于点E
(1)求证:△ABD∽△DCE;
(2)若AB=15,tanB=;
①求BC的长;
②如图2,当DE//AB时,过点A作AF⊥AD交射线DE于点F,连接CF,求AE的长
【答案】
【解析】(1)∵AB=AC,∴∠B=∠ACB,∵∠ADE+∠CDE=∠B+∠BAD,∠ADE=∠B,∴∠BAD=∠CDE,
∴△BAD∽△DCE;
(2)如图2中,作AM⊥BC于M.
在Rt△ABM中,设BM=4k,∵tanB==,∴AM=BM?tanB=4k×=3k,由勾股定理,得到AB2=AM2+BM2,
∴152=(3k)2+(4k)2,∴k=3或-3(舍弃),∴AM=9,BM=12,∵AB=AC,AM⊥BC,∴BC=2BM=2×4k=24,
(3)点D在BC边上运动的过程中,存在某个位置,使得DF=CF.
∵DE∥AB,∴∠BAD=∠ADE,∵∠ADE=∠B,∠B=∠ACB,∴∠BAD=∠ACB,∵∠ABD=∠CBA,∴△ABD∽△CBA,
∴AB:CB=DB:AB,∴DB===,∵DE∥AB,∴AE:AC=BD:BC,∴AE===.
七、(本题满分12分)
22、如图,已知二次函数图象的顶点为C(1,0),直线y=x+m与该二次函数的图象交于A、B两点,其中点A的坐标为(3,4),点B在y轴上。
(1)求m的值及这个二次函数的表达式;
(2)P为线段AB上的一个动点(点P与点A、B不重合),过点P作x轴的垂线与这个二次函数的图象交于点E,设线段PE的长为h,点P的横坐标为x
①求h与x之间的函数关系式,并写出自变量x的取值范围;
②线段PE的长h是否存在最大值?若存在,请求出它的最大值及此时的x值;若不存在,请说明理由。
【答案】
【解析】(1)∵点A(3,4)在直线y=x+m上,∴4=3+m.∴m=1.设所求二次函数的关系式为y=a(x-1)2.
∵点A(3,4)在二次函数y=a(x-1)2的图象上,∴4=a(3-1)2,∴a=1.
∴所求二次函数的关系式为y=(x-1)2.即y=x2-2x+1.
(2)①设P、E两点的纵坐标分别为yP和yE.∴PE=h=yP-yE=(x+1)-(x2-2x+1)=-x2+3x.
即h=-x2+3x(0<x<3).
②存在.∵h=-(x-)2+,又∵a=-1<0,∴x=时,h的值最大,最大值为.
八、(本题满分14分)
23、在△ABC中,AE⊥CD且AE=CD,∠CAE+2∠BAE=
90°.
(1)如图1,若△ACE为等边三角形,CD=2,求AB的长。
(2)如图2,过点E作EG⊥AB,垂足为G
①求证:AD=BE;
②如图3,当点D与点G重合时,连接BF,请求出的值;
【答案】
【解析】(1)∵若△ACE为等边三角形,∴AC=AE=CD=2,且∠CEA=∠CAE=60°,∵∠CAE+2∠BAE=
90°,∴∠BAE=15°,
∠B=45°,过点A作AK⊥BC,垂足为K,则AK=×AC=,且AB=AK=;
(2)①过点C作CM⊥AB,M为垂足,设∠BAE=β,∵∠CAE+2∠BAE=
90°,∴∠CAE=90°-2β,∵AE⊥CD,
∴∠ACD=2β,∵AE⊥CD,∴∠CAE=90°-[90°-2β+β]=
β,∴∠DCM=∠ACM=∠BAE=
β,CM=CM,
∠CMD=∠CMA=90°,∴△AMC≌△DMC,∴AM=DM,且AC=CD=AE,在△AGE与△AMC中,∠ACM=∠BAE,
∠AGE=∠CMA=90°,AC=AE,
∴△AMC≌△EGA,∴AM=EG,
∴EGAD,在等腰△AEC中,∠EAC=90°-β,
∴∠AEC=45°+β,∴∠B=45°,∵EG⊥AB,∴BE=EG=×AD,即AD=BE;
②过点C、F分别作CM⊥AB、FH⊥AB,垂足为M、H,则ED//FH//CM;由①知:AM=MD=BD=DE,设BD=a,AM=DM=DE=a,
AD=2a,由勾股定理得到:BE=a,AE=a;则DF=a,
EF=a,
AF=a,
∵FH//ED,∴△AHF∽△ADE,
∴FH:DE=AF:AE=AH:AD,解得:FH=a;
AH=a;
则BH=a;
由勾股定理:BF=a,;=,
同课章节目录
