华东师大版七年级上册 5.2.2 平行线 的判定课件(共19张PPT)
文档属性
| 名称 | 华东师大版七年级上册 5.2.2 平行线 的判定课件(共19张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 491.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-12-25 14:29:07 | ||
图片预览



文档简介
(共19张PPT)
平行线的判定
学习目标
1.掌握平行线的判定方法.
2.能应用平行线的判定方法判定两
直线平行.
3.了解推理、证明的格式,能进行
简单的逻辑推理.
设疑自探
同学们,根据本节课题结合学习目标,你有那些问题,请提出来。
1.掌握平行线的判定方法.
2.能应用平行线的判定方法判定两
直线平行.
3.了解推理、证明的格式,能进行
简单的逻辑推理.
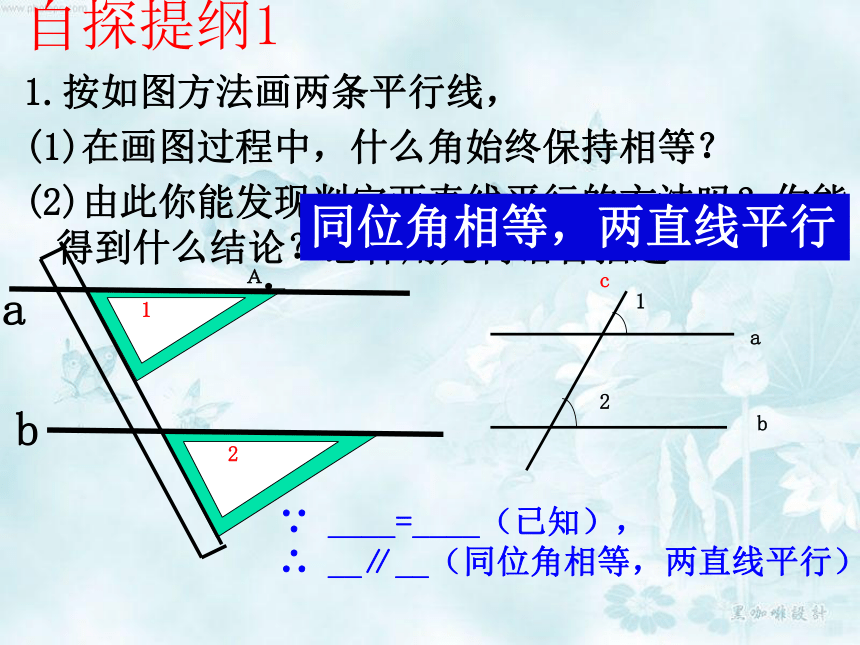
自探提纲1
1.按如图方法画两条平行线,
(1)在画图过程中,什么角始终保持相等?
(2)由此你能发现判定两直线平行的方法吗?你能得到什么结论?怎样用几何语言描述?
1
2
a
b
.
A
c
a
b
1
2
∵
____=____(已知),
∴
__∥__(同位角相等,两直线平行).
同位角相等,两直线平行
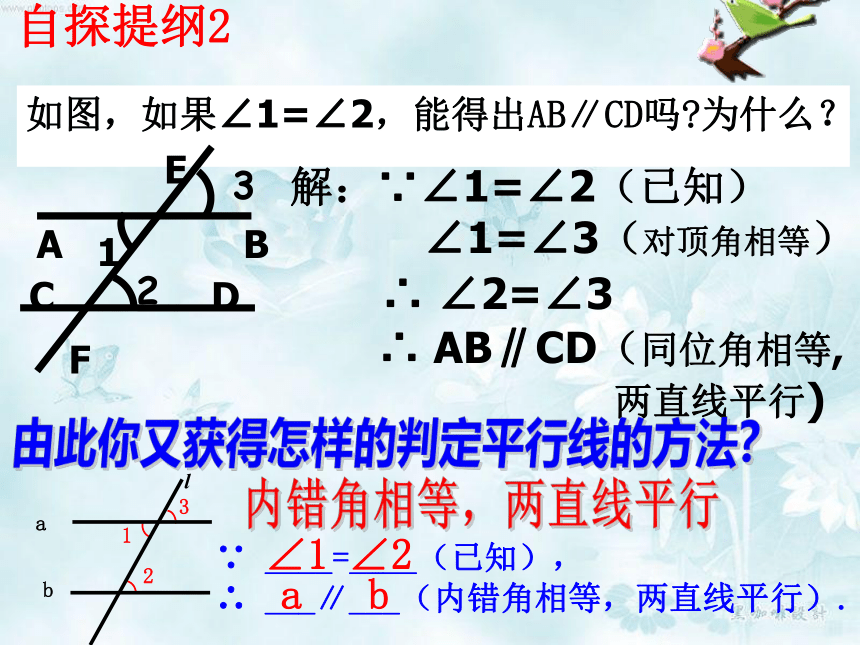
如图,如果∠1=∠2,能得出AB∥CD吗?为什么?
解:∵∠1=∠2(已知)
∠1=∠3(对顶角相等)
∴
∠2=∠3
∴
AB∥CD(同位角相等,
两直线平行)
B
1
A
C
D
F
3
2
E
由此你又获得怎样的判定平行线的方法?
自探提纲2
a
b
l
2
1
3
∵
____=____(已知),
∴
___∥___(内错角相等,两直线平行).
内错角相等,两直线平行
∠1
∠2
a
b
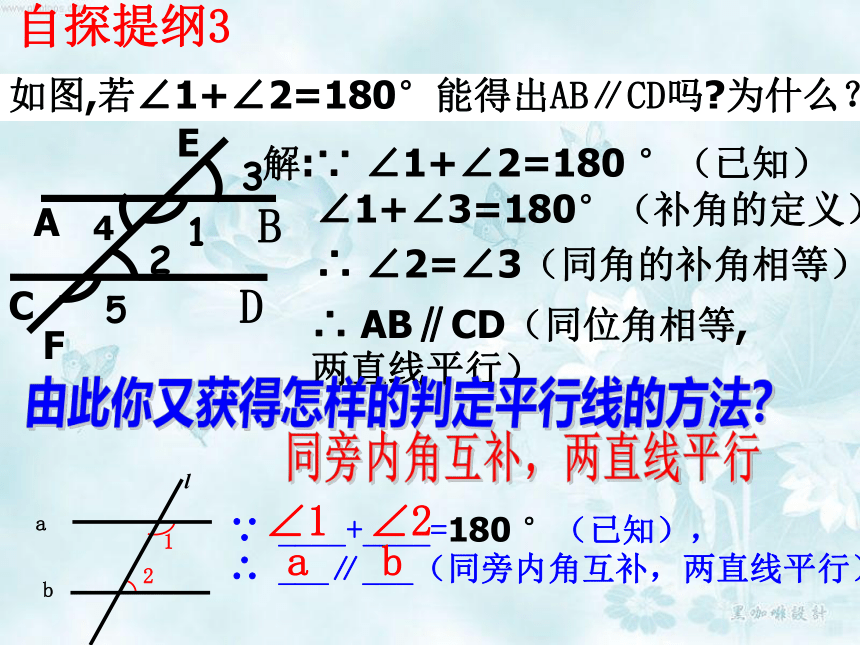
如图,若∠1+∠2=180°能得出AB∥CD吗?为什么?
解:∵
∠1+∠2=180
°(已知)
∠1+∠3=180°(补角的定义)
∴
∠2=∠3(同角的补角相等)
∴
AB∥CD(同位角相等,
两直线平行)
4
A
C
3
1
2
5
D
B
E
F
自探提纲3
由此你又获得怎样的判定平行线的方法?
同旁内角互补,两直线平行
a
b
l
2
1
∵
____+____=180
°(已知),
∴
___∥___(同旁内角互补,两直线平行).
∠1
∠2
a
b
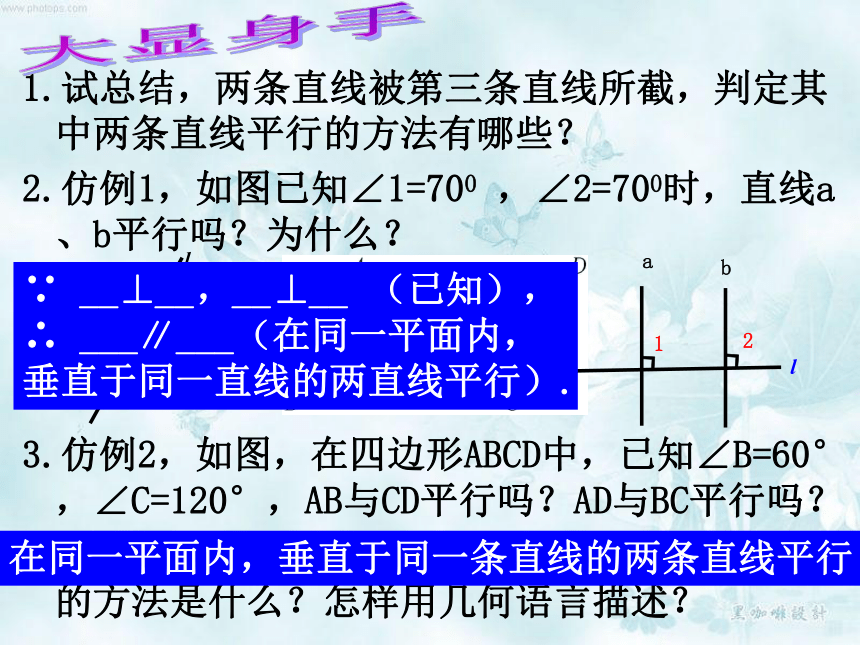
1.试总结,两条直线被第三条直线所截,判定其中两条直线平行的方法有哪些?
2.仿例1,如图已知∠1=700
,∠2=700时,直线a、b平行吗?为什么?
3.仿例2,如图,在四边形ABCD中,已知∠B=60°,∠C=120°,AB与CD平行吗?AD与BC平行吗?
4.完成例3,由此例我们可以得到判定两直线平行的方法是什么?怎样用几何语言描述?
a
b
l
2
1
a
b
l
1
2
┓
┓
在同一平面内,垂直于同一条直线的两条直线平行
∵
__⊥__,__⊥__
(已知),
∴
___∥___(在同一平面内,
垂直于同一直线的两直线平行).
大显身手
①
∵
∠2
=____(已知),
∴
___∥___
(
)
②
∵
∠3
=
(已知),
∴
___∥___(
)
③
∵
∠4
+
=180°(已知),
∴
___∥___(
)
∠6
AB
CD
AB
CD
∠5
AB
CD
A
C
1
4
2
3
5
8
6
7
B
D
1.如图:
同位角相等,两直线平行
内错角相等,两直线平行
同旁内角互补,两直线平行
∠5
小试牛刀
1.完成课后练习1.2.4
2.
如图:已知
∠1=75°
,
∠2
=105°
问:直线AB与CD平行吗?为什么?
A
C
1
4
2
3
B
D
5
大显身手
(1)
∵
∠1
=
_____(已知),
∴
AB∥CE(
)
(2)
∵
∠1
+
_____=180°(已知),
∴
CD∥BF(
)
3.如图:
1
3
5
4
2
C
F
E
A
D
B
(3)
∵
∠1
+∠5
=180°(已知),
∴
_____∥_____(
)
(4)
∵
∠4
+_____=180°(已知),
∴
CE∥AB(
)
如图,AD平分∠BAC,
∠1=∠3,能推出AB∥CD吗?说明理由。
2
1
3
B
C
D
A
(第2题)
解:∵
AD平分∠BAC,
∴∠1=∠2
(角平分线的定义)
又∵
∠1=
∠3,
∴
∠2=
∠3
(等量代换)
∴AB∥CD(内错角相等,两直线平行。)
勇攀高峰
如图,已知∠ABD=∠ACE,BF、CG分别是∠ABD、∠ACE的平分线,请判断BF与CG是否平行,并说明理由。
1
A
B
C
D
E
F
G
2
能力拓展
平行线的判定示意图
同位角相等
内错角相等
同旁内角互补
两直线平行
判定
数量关系
位置关系
知识的升华
独立
作业
驶向胜利的彼岸
P179
3.(抄写解题过程)4.
如图,直线a
∥b,b∥c,c∥d,那么a
∥d吗?为什么?
a
b
c
d
解:
因为
a
∥b,b∥c,
所以
a
∥c
(
)
如果两条直线都与第三条直线平行,那么这两条直线互相平行
如果两条直线都与第三条直线平行,那么这两条直线互相平行
因为
c∥d,
所以
a
∥d
(
)
能力拓展
三角形个数=多边形边数-1
如果从多边形边上一点,连接多边形的各个顶点分割三角形,n边形可分割成多少个三角形?
能力拓展
如果沿着在三角形内部找一点,连接多边形的各个顶点,那么n边形可以分割成多少个三角形?
三角形个数=多边形边数
挑战自我
能力拓展
有两个多项式:
A=2a2
-4a+1,
B=2(a2
-2a)+3,当a取任意有理数时,请比较A与B的大小.
解:
∵A-B
=
(2a2-4a+1
)-
[2(a2-2a)+3]
=
(2a2
-4a+1
)-
(2a2
-4a+3)
=
2a2
-4a+1
-
2a2
+4a-3
=
(2a2
-
2a2
)-(4a+4a
)+(1-3)
=
-2<0
∴
A
-B
<
0
∴
A
<
B
挑战自我
平行线的判定
学习目标
1.掌握平行线的判定方法.
2.能应用平行线的判定方法判定两
直线平行.
3.了解推理、证明的格式,能进行
简单的逻辑推理.
设疑自探
同学们,根据本节课题结合学习目标,你有那些问题,请提出来。
1.掌握平行线的判定方法.
2.能应用平行线的判定方法判定两
直线平行.
3.了解推理、证明的格式,能进行
简单的逻辑推理.
自探提纲1
1.按如图方法画两条平行线,
(1)在画图过程中,什么角始终保持相等?
(2)由此你能发现判定两直线平行的方法吗?你能得到什么结论?怎样用几何语言描述?
1
2
a
b
.
A
c
a
b
1
2
∵
____=____(已知),
∴
__∥__(同位角相等,两直线平行).
同位角相等,两直线平行
如图,如果∠1=∠2,能得出AB∥CD吗?为什么?
解:∵∠1=∠2(已知)
∠1=∠3(对顶角相等)
∴
∠2=∠3
∴
AB∥CD(同位角相等,
两直线平行)
B
1
A
C
D
F
3
2
E
由此你又获得怎样的判定平行线的方法?
自探提纲2
a
b
l
2
1
3
∵
____=____(已知),
∴
___∥___(内错角相等,两直线平行).
内错角相等,两直线平行
∠1
∠2
a
b
如图,若∠1+∠2=180°能得出AB∥CD吗?为什么?
解:∵
∠1+∠2=180
°(已知)
∠1+∠3=180°(补角的定义)
∴
∠2=∠3(同角的补角相等)
∴
AB∥CD(同位角相等,
两直线平行)
4
A
C
3
1
2
5
D
B
E
F
自探提纲3
由此你又获得怎样的判定平行线的方法?
同旁内角互补,两直线平行
a
b
l
2
1
∵
____+____=180
°(已知),
∴
___∥___(同旁内角互补,两直线平行).
∠1
∠2
a
b
1.试总结,两条直线被第三条直线所截,判定其中两条直线平行的方法有哪些?
2.仿例1,如图已知∠1=700
,∠2=700时,直线a、b平行吗?为什么?
3.仿例2,如图,在四边形ABCD中,已知∠B=60°,∠C=120°,AB与CD平行吗?AD与BC平行吗?
4.完成例3,由此例我们可以得到判定两直线平行的方法是什么?怎样用几何语言描述?
a
b
l
2
1
a
b
l
1
2
┓
┓
在同一平面内,垂直于同一条直线的两条直线平行
∵
__⊥__,__⊥__
(已知),
∴
___∥___(在同一平面内,
垂直于同一直线的两直线平行).
大显身手
①
∵
∠2
=____(已知),
∴
___∥___
(
)
②
∵
∠3
=
(已知),
∴
___∥___(
)
③
∵
∠4
+
=180°(已知),
∴
___∥___(
)
∠6
AB
CD
AB
CD
∠5
AB
CD
A
C
1
4
2
3
5
8
6
7
B
D
1.如图:
同位角相等,两直线平行
内错角相等,两直线平行
同旁内角互补,两直线平行
∠5
小试牛刀
1.完成课后练习1.2.4
2.
如图:已知
∠1=75°
,
∠2
=105°
问:直线AB与CD平行吗?为什么?
A
C
1
4
2
3
B
D
5
大显身手
(1)
∵
∠1
=
_____(已知),
∴
AB∥CE(
)
(2)
∵
∠1
+
_____=180°(已知),
∴
CD∥BF(
)
3.如图:
1
3
5
4
2
C
F
E
A
D
B
(3)
∵
∠1
+∠5
=180°(已知),
∴
_____∥_____(
)
(4)
∵
∠4
+_____=180°(已知),
∴
CE∥AB(
)
如图,AD平分∠BAC,
∠1=∠3,能推出AB∥CD吗?说明理由。
2
1
3
B
C
D
A
(第2题)
解:∵
AD平分∠BAC,
∴∠1=∠2
(角平分线的定义)
又∵
∠1=
∠3,
∴
∠2=
∠3
(等量代换)
∴AB∥CD(内错角相等,两直线平行。)
勇攀高峰
如图,已知∠ABD=∠ACE,BF、CG分别是∠ABD、∠ACE的平分线,请判断BF与CG是否平行,并说明理由。
1
A
B
C
D
E
F
G
2
能力拓展
平行线的判定示意图
同位角相等
内错角相等
同旁内角互补
两直线平行
判定
数量关系
位置关系
知识的升华
独立
作业
驶向胜利的彼岸
P179
3.(抄写解题过程)4.
如图,直线a
∥b,b∥c,c∥d,那么a
∥d吗?为什么?
a
b
c
d
解:
因为
a
∥b,b∥c,
所以
a
∥c
(
)
如果两条直线都与第三条直线平行,那么这两条直线互相平行
如果两条直线都与第三条直线平行,那么这两条直线互相平行
因为
c∥d,
所以
a
∥d
(
)
能力拓展
三角形个数=多边形边数-1
如果从多边形边上一点,连接多边形的各个顶点分割三角形,n边形可分割成多少个三角形?
能力拓展
如果沿着在三角形内部找一点,连接多边形的各个顶点,那么n边形可以分割成多少个三角形?
三角形个数=多边形边数
挑战自我
能力拓展
有两个多项式:
A=2a2
-4a+1,
B=2(a2
-2a)+3,当a取任意有理数时,请比较A与B的大小.
解:
∵A-B
=
(2a2-4a+1
)-
[2(a2-2a)+3]
=
(2a2
-4a+1
)-
(2a2
-4a+3)
=
2a2
-4a+1
-
2a2
+4a-3
=
(2a2
-
2a2
)-(4a+4a
)+(1-3)
=
-2<0
∴
A
-B
<
0
∴
A
<
B
挑战自我
同课章节目录
- 第1章 走进数学世界
- 数学伴我们成长
- 人类离不开数学
- 人人都能学会数学
- 第2章 有理数
- 2.1 有理数
- 2.2 数轴
- 2.3 相反数
- 2.4 绝对值
- 2.5 有理数的大小比较
- 2.6 有理数的加法
- 2.7 有理数的减法
- 2.8 有理数加减混合运算
- 2.9 有理数的乘法
- 2.10 有理数的除法
- 2.11 有理数的乘方
- 2.12 科学记数法
- 2.13 有理数的混合运算
- 2.14 近似数
- 2.15 用计算器进行计算
- 第3章 整式的加减
- 3.1 列代数式
- 3.2 代数式的值
- 3.3 整式
- 3.4 整式的加减
- 第4章 图形的初步认识
- 4.1 生活中的立体图形
- 4.2 立体图形的视图
- 4.3 立体图形的表面展开图
- 4.4 平面图形
- 4.5 最基本的图形——点和线
- 4.6 角
- 第5章 相交线与平行线
- 5.1 相交线
- 5.2 平行线
