湘教版九下数学2.7正多边形与圆课件(29张ppt)
文档属性
| 名称 | 湘教版九下数学2.7正多边形与圆课件(29张ppt) |  | |
| 格式 | zip | ||
| 文件大小 | 746.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-12-25 14:31:47 | ||
图片预览



文档简介
(共29张PPT)
正多边形与圆
一、
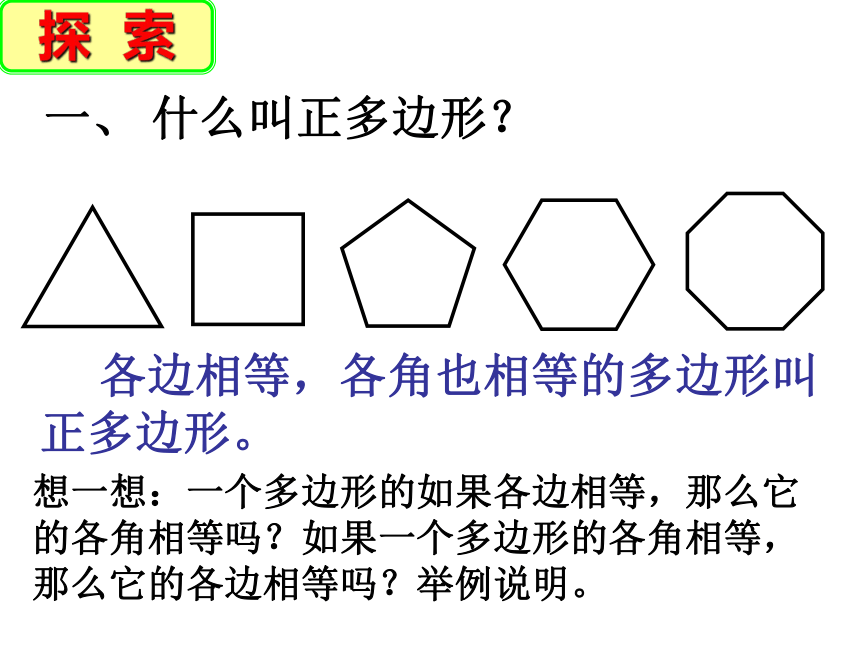
什么叫正多边形?
各边相等,各角也相等的多边形叫
正多边形。
探
索
想一想:一个多边形的如果各边相等,那么它的各角相等吗?如果一个多边形的各角相等,那么它的各边相等吗?举例说明。
二、
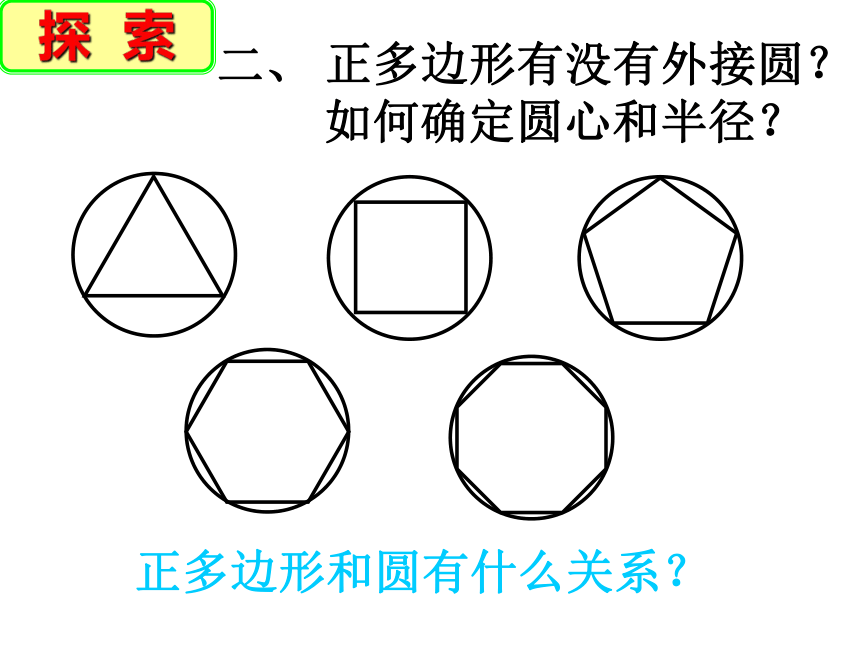
正多边形有没有外接圆?
如何确定圆心和半径?
正多边形和圆有什么关系?
探
索
三、
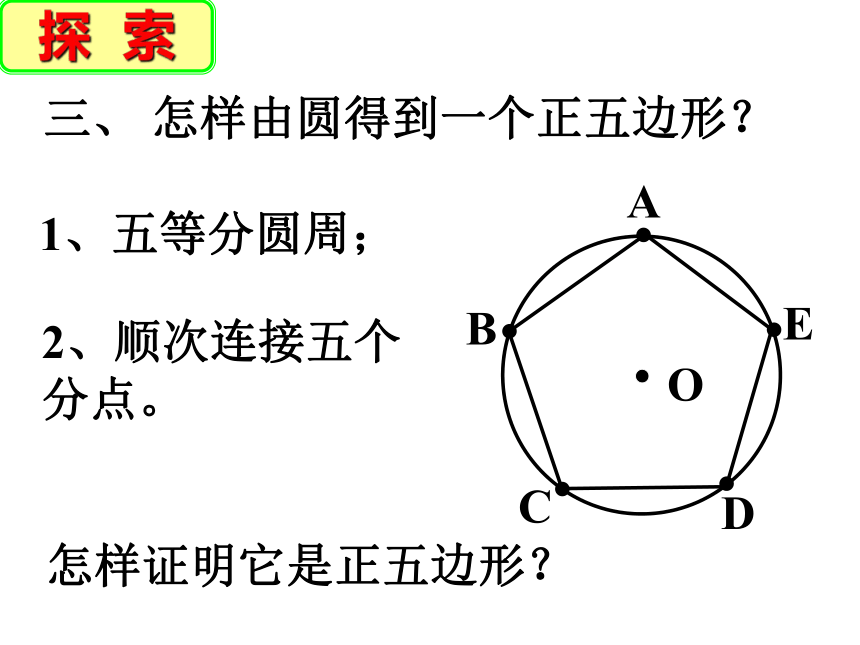
怎样由圆得到一个正五边形?
O
A
B
C
D
E
1、五等分圆周;
2、顺次连接五个
分点。
怎样证明它是正五边形?
探
索
四、
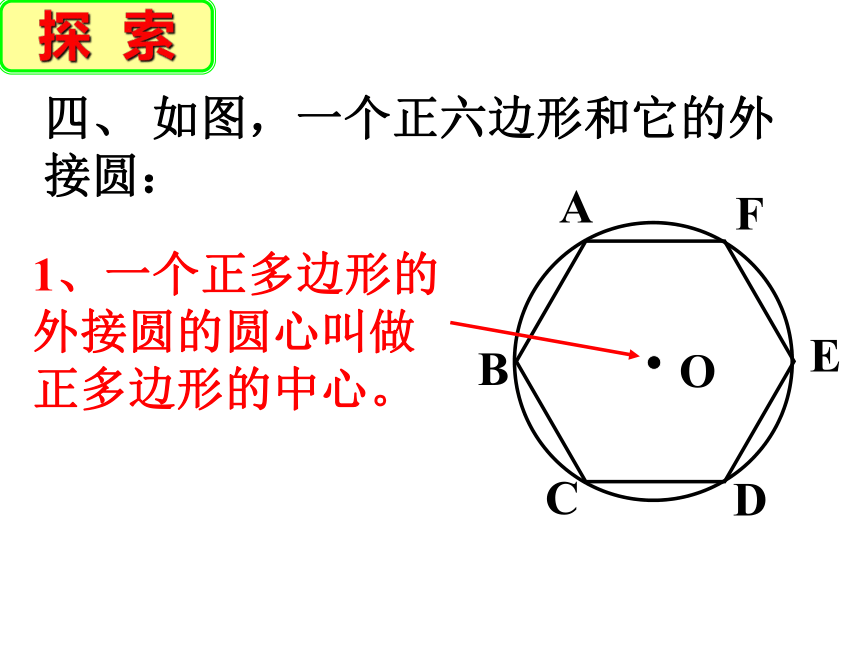
如图,一个正六边形和它的外
接圆:
O
A
B
C
D
E
F
1、一个正多边形的
外接圆的圆心叫做
正多边形的中心。
探
索
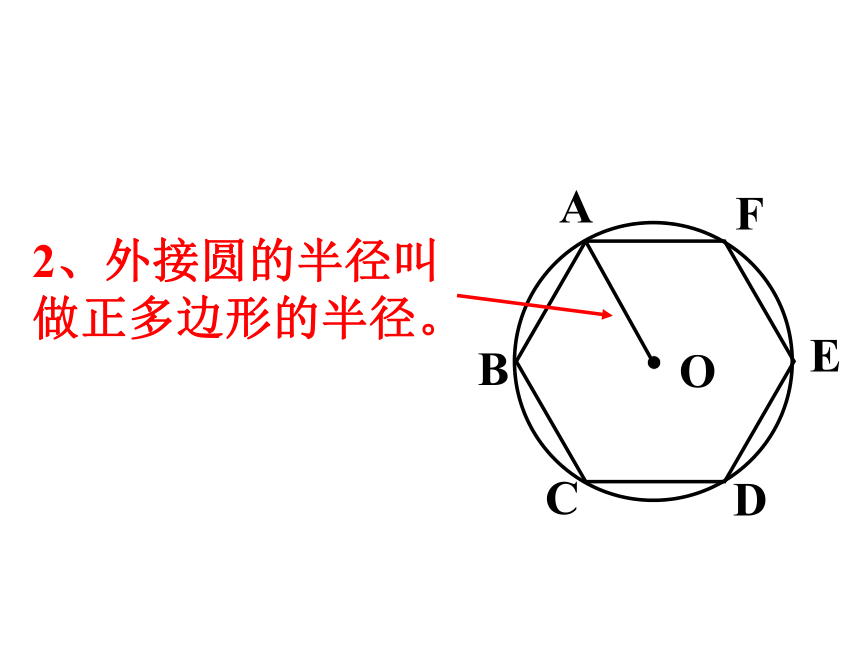
2、外接圆的半径叫
做正多边形的半径。
O
A
B
C
D
E
F
3、正多边形每一边
所对的圆心角叫做
正多边形的中心角。
O
A
B
C
D
E
F
正n边形的中心角:
正n边形的每一个外角等于多少?
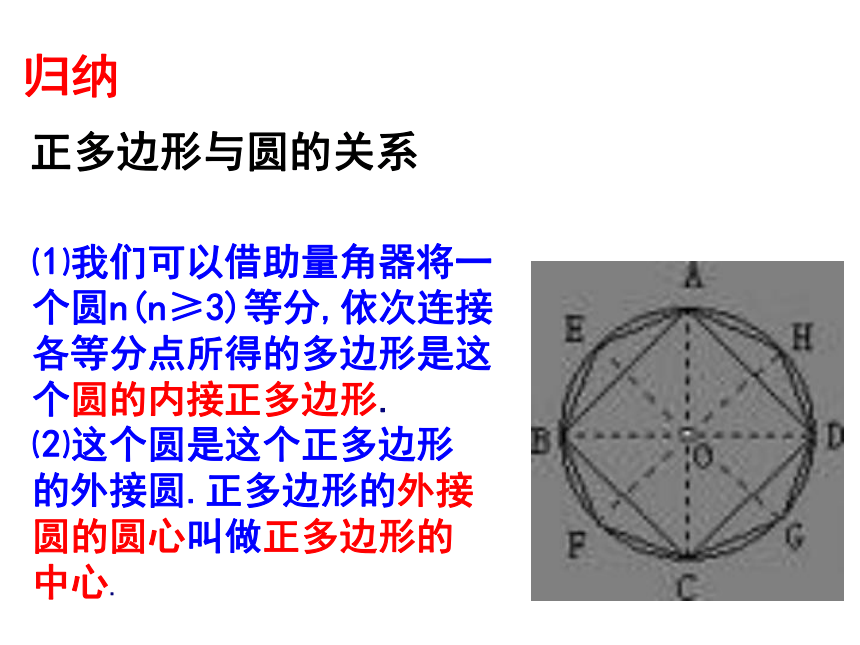
正多边形与圆的关系
⑴我们可以借助量角器将一个圆n(n≥3)等分,依次连接各等分点所得的多边形是这个圆的内接正多边形.
⑵这个圆是这个正多边形的外接圆.正多边形的外接圆的圆心叫做正多边形的中心.
归纳
正多边形对称性
交流:你认为正多边形都是对称性
归纳:正多边形都是轴对称图形,一个正n边形
共有n条对称轴,每条对称轴都通过n边形
的中心。
探索交流
边数是偶数的正多边形还是中心
对称图形,它的中心就是对称中心。
正多边形的性质:
1.正多边形的各边相等,各角相等.
2.正多边形都是轴对称图形,一个正n边形有n条对称轴,每条对称轴都通过正多边形的中心;正多边形的边数是偶数时,它既是轴对称图形,也是中心对称图形,它的中心就是对称中心。
3.边数相同的正多边形相似
2、正多边形内切圆的半径叫做边心距.
正多边形外接圆的半径叫做正多边形的半径.
3、正多边形的一边所对正多边形外接圆的圆心角叫做中心角
4、正n边形的每个内角等于多少?每个外角等于多少?中心角等于多少?
1、正多边形的外接圆与内切圆的圆心互相重合
1、正方形ABCD的内切圆⊙O的半径OE叫做正方形ABCD的______.
2、若正六边形的边长为1,
那么正六边形的中心角是___度,半径是______,边心距是
,
它的每一个内角是______.
3、正n边形的一个外角度数与它的______角的度数相等.
边心距
60
1
120°
中心
1.正四边形
O
2正六边形
O
如何画一个边长为2cm的正六边
形?
O
A
B
C
D
E
F
1、以2cm为半径作
一个⊙
O;
2、用量角器画一个
60°的圆心角;
3、在圆上顺次截取这个圆心角对的弧;
4、顺次连接分点。
思考
用尺规作一个正三角形。
由此你还能作哪些正多边形?
练
习
如何作正十二边形,正八边形?
例1、如图,有一个亭子,它的地基是
半径为4cm的正六边形,求地基的周长
和面积(精确到0.1cm2)。
O
A
B
C
D
E
F
P
典型例题
例2、如图,正六边形ABCDEF的半径为
8cm,求这个正六边形的边长。
O
A
B
C
D
E
F
例3、正三角形的半径为R,则边长为
,
边心距为
,面积为
。
例4、正三角形的边长a,则其半径为
。
1、已知圆内接正方形的面积为8,求
圆内接正六边形的面积。
O
A
B
C
D
E
F
巩固练习
2、同圆的内接正三角形、正四边形、
正六边形的边长之比为
。
巩固练习
如图,△ABC是⊙O的内接等腰
三角形,顶角∠BAC=36°,弦BD、
CE分别平分∠ABC,
∠ACB。
求证:五边形
AEBCD是正
五边形。
O
A
E
B
C
D
巩固练习
1.正方形ABCD的外接圆圆心O叫做正方形ABCD的______.
中心
2.正多边形一定是
对称图形,一个正n边形共有
条对称轴,每条对称轴都通过
;如果一个正n边形是中心对称图形,n一定是
.
3.将一个正五边形绕它的中心旋转,至少要旋转
度,才能与原来的图形位置重合.
轴
n
中心
偶数
72
4.下列说法中正确的是(
)
A.平行四边形是正多边形
B.
矩形是正四边形
C.
菱形是正四边形
D.
正方形是正四边形
5.
下列命题中,真命题的个数是(
)
①各边都相等的多边形是正多边形;
②各角都相等的多边形是正多边形;
③正多边形一定是中心对称图形;
④边数相同的正多边形一定相似.
A.1
B.2
C.
3
D.
4
D
A
6.已知正n边形的一个外角与一个内角的比为1﹕3,则n等于(
)
A.
4
B.
6
C.
8
D.
12
7.
如果一个正多边形绕它的中心旋转90°就和原来的图形重合,那么这个正多边形是(
)
A.正三角形
B.正方形
C.正五边形
D.正六边形
C
B
8.两个正三角形的内切圆的半径分别为12和18,这两个三角形的周长之比为
,面积之比为
.
2﹕3
4﹕9
9.
P144练习
1,2
你会计算五角星的每个锐角的度数吗?
1.正多边形和圆的有关概念
2.正多边形的基本图形
3.正多边形的画法
归纳总结
正多边形与圆
一、
什么叫正多边形?
各边相等,各角也相等的多边形叫
正多边形。
探
索
想一想:一个多边形的如果各边相等,那么它的各角相等吗?如果一个多边形的各角相等,那么它的各边相等吗?举例说明。
二、
正多边形有没有外接圆?
如何确定圆心和半径?
正多边形和圆有什么关系?
探
索
三、
怎样由圆得到一个正五边形?
O
A
B
C
D
E
1、五等分圆周;
2、顺次连接五个
分点。
怎样证明它是正五边形?
探
索
四、
如图,一个正六边形和它的外
接圆:
O
A
B
C
D
E
F
1、一个正多边形的
外接圆的圆心叫做
正多边形的中心。
探
索
2、外接圆的半径叫
做正多边形的半径。
O
A
B
C
D
E
F
3、正多边形每一边
所对的圆心角叫做
正多边形的中心角。
O
A
B
C
D
E
F
正n边形的中心角:
正n边形的每一个外角等于多少?
正多边形与圆的关系
⑴我们可以借助量角器将一个圆n(n≥3)等分,依次连接各等分点所得的多边形是这个圆的内接正多边形.
⑵这个圆是这个正多边形的外接圆.正多边形的外接圆的圆心叫做正多边形的中心.
归纳
正多边形对称性
交流:你认为正多边形都是对称性
归纳:正多边形都是轴对称图形,一个正n边形
共有n条对称轴,每条对称轴都通过n边形
的中心。
探索交流
边数是偶数的正多边形还是中心
对称图形,它的中心就是对称中心。
正多边形的性质:
1.正多边形的各边相等,各角相等.
2.正多边形都是轴对称图形,一个正n边形有n条对称轴,每条对称轴都通过正多边形的中心;正多边形的边数是偶数时,它既是轴对称图形,也是中心对称图形,它的中心就是对称中心。
3.边数相同的正多边形相似
2、正多边形内切圆的半径叫做边心距.
正多边形外接圆的半径叫做正多边形的半径.
3、正多边形的一边所对正多边形外接圆的圆心角叫做中心角
4、正n边形的每个内角等于多少?每个外角等于多少?中心角等于多少?
1、正多边形的外接圆与内切圆的圆心互相重合
1、正方形ABCD的内切圆⊙O的半径OE叫做正方形ABCD的______.
2、若正六边形的边长为1,
那么正六边形的中心角是___度,半径是______,边心距是
,
它的每一个内角是______.
3、正n边形的一个外角度数与它的______角的度数相等.
边心距
60
1
120°
中心
1.正四边形
O
2正六边形
O
如何画一个边长为2cm的正六边
形?
O
A
B
C
D
E
F
1、以2cm为半径作
一个⊙
O;
2、用量角器画一个
60°的圆心角;
3、在圆上顺次截取这个圆心角对的弧;
4、顺次连接分点。
思考
用尺规作一个正三角形。
由此你还能作哪些正多边形?
练
习
如何作正十二边形,正八边形?
例1、如图,有一个亭子,它的地基是
半径为4cm的正六边形,求地基的周长
和面积(精确到0.1cm2)。
O
A
B
C
D
E
F
P
典型例题
例2、如图,正六边形ABCDEF的半径为
8cm,求这个正六边形的边长。
O
A
B
C
D
E
F
例3、正三角形的半径为R,则边长为
,
边心距为
,面积为
。
例4、正三角形的边长a,则其半径为
。
1、已知圆内接正方形的面积为8,求
圆内接正六边形的面积。
O
A
B
C
D
E
F
巩固练习
2、同圆的内接正三角形、正四边形、
正六边形的边长之比为
。
巩固练习
如图,△ABC是⊙O的内接等腰
三角形,顶角∠BAC=36°,弦BD、
CE分别平分∠ABC,
∠ACB。
求证:五边形
AEBCD是正
五边形。
O
A
E
B
C
D
巩固练习
1.正方形ABCD的外接圆圆心O叫做正方形ABCD的______.
中心
2.正多边形一定是
对称图形,一个正n边形共有
条对称轴,每条对称轴都通过
;如果一个正n边形是中心对称图形,n一定是
.
3.将一个正五边形绕它的中心旋转,至少要旋转
度,才能与原来的图形位置重合.
轴
n
中心
偶数
72
4.下列说法中正确的是(
)
A.平行四边形是正多边形
B.
矩形是正四边形
C.
菱形是正四边形
D.
正方形是正四边形
5.
下列命题中,真命题的个数是(
)
①各边都相等的多边形是正多边形;
②各角都相等的多边形是正多边形;
③正多边形一定是中心对称图形;
④边数相同的正多边形一定相似.
A.1
B.2
C.
3
D.
4
D
A
6.已知正n边形的一个外角与一个内角的比为1﹕3,则n等于(
)
A.
4
B.
6
C.
8
D.
12
7.
如果一个正多边形绕它的中心旋转90°就和原来的图形重合,那么这个正多边形是(
)
A.正三角形
B.正方形
C.正五边形
D.正六边形
C
B
8.两个正三角形的内切圆的半径分别为12和18,这两个三角形的周长之比为
,面积之比为
.
2﹕3
4﹕9
9.
P144练习
1,2
你会计算五角星的每个锐角的度数吗?
1.正多边形和圆的有关概念
2.正多边形的基本图形
3.正多边形的画法
归纳总结
