沪教版(上海)数学九年级第二学期-27.3 垂径定理(1) 课件(20张PPT)
文档属性
| 名称 | 沪教版(上海)数学九年级第二学期-27.3 垂径定理(1) 课件(20张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 476.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-12-25 16:52:31 | ||
图片预览





文档简介
(共20张PPT)
赵州石拱桥
一千三百多年前,我国隋代建造的赵州石拱桥的桥拱是圆弧形,它的跨度(弧所对的弦的长)为37.4米,
拱高(弧的中点到弦的距离,也叫弓形高)为7.2米.
你会求桥拱所在圆的半径长吗?
§27.3
垂径定理(1)
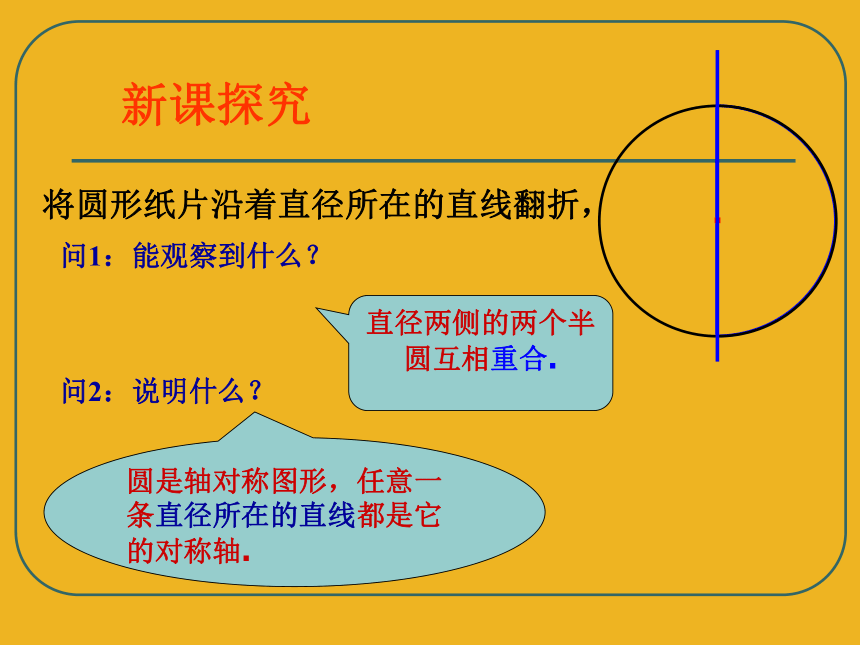
将圆形纸片沿着直径所在的直线翻折,
新课探究
问1:能观察到什么?
问2:说明什么?
直径两侧的两个半圆互相重合.
圆是轴对称图形,任意一条直径所在的直线都是它的对称轴.
·
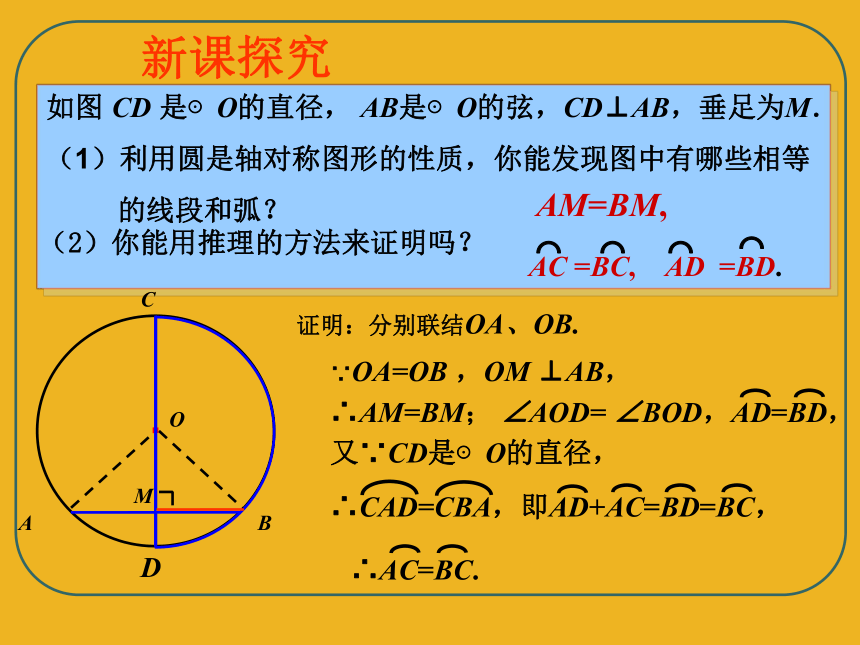
如图
CD
是⊙O的直径,
AB是⊙O的弦,CD⊥AB,垂足为M.
(1)利用圆是轴对称图形的性质,你能发现图中有哪些相等
的线段和弧?
(2)你能用推理的方法来证明吗?
新课探究
证明:分别联结OA、OB.
∵OA=OB
,OM
⊥AB,
又∵CD是⊙O的直径,
AM=BM,
⌒
⌒
AC
=BC,
⌒
⌒
AD
=BD.
∴CAD=CBA,即AD+AC=BD=BC,
∴AM=BM;
∠AOD=
∠BOD,AD=BD,
∴AC=BC.
·
O
A
B
C
M
D
B
C
A
M
O
.
D
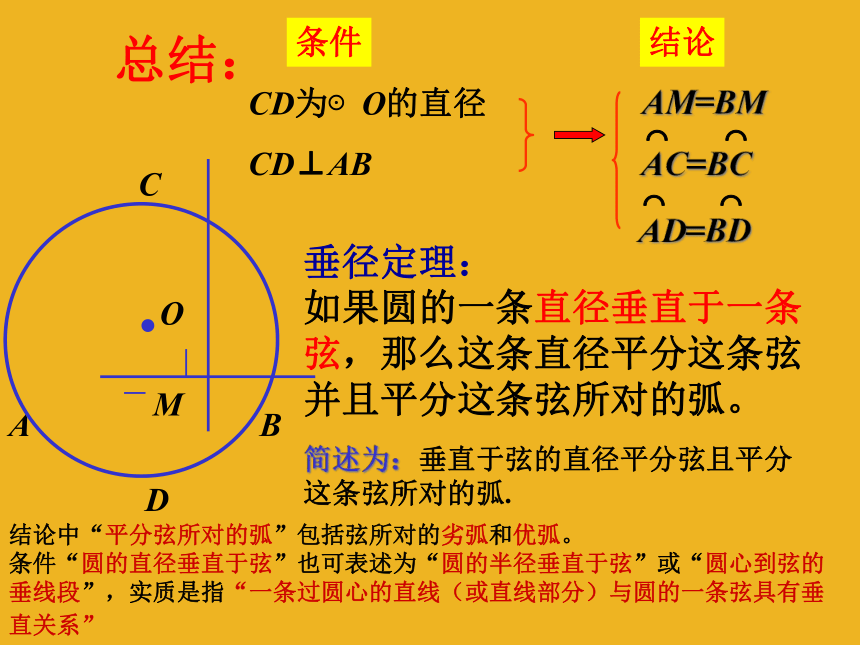
总结:
垂径定理:
如果圆的一条直径垂直于一条弦,那么这条直径平分这条弦并且平分这条弦所对的弧。
CD为⊙O的直径
CD⊥AB
条件
结论
⌒
⌒
⌒
⌒
AM=BM
AC=BC
AD=BD
结论中“平分弦所对的弧”包括弦所对的劣弧和优弧。
条件“圆的直径垂直于弦”也可表述为“圆的半径垂直于弦”或“圆心到弦的垂线段”,实质是指“一条过圆心的直线(或直线部分)与圆的一条弦具有垂直关系”
简述为:垂直于弦的直径平分弦且平分这条弦所对的弧.
垂径定理的符号语言
●O
A
B
C
D
M└
CD⊥AB,
∵
CD过圆心,
∴AM=BM,
⌒
⌒
AC
=BC,
⌒
⌒
AD
=BD(垂径定理)
E
O
A
B
D
C
E
O
A
B
C
O
B
A
E
D
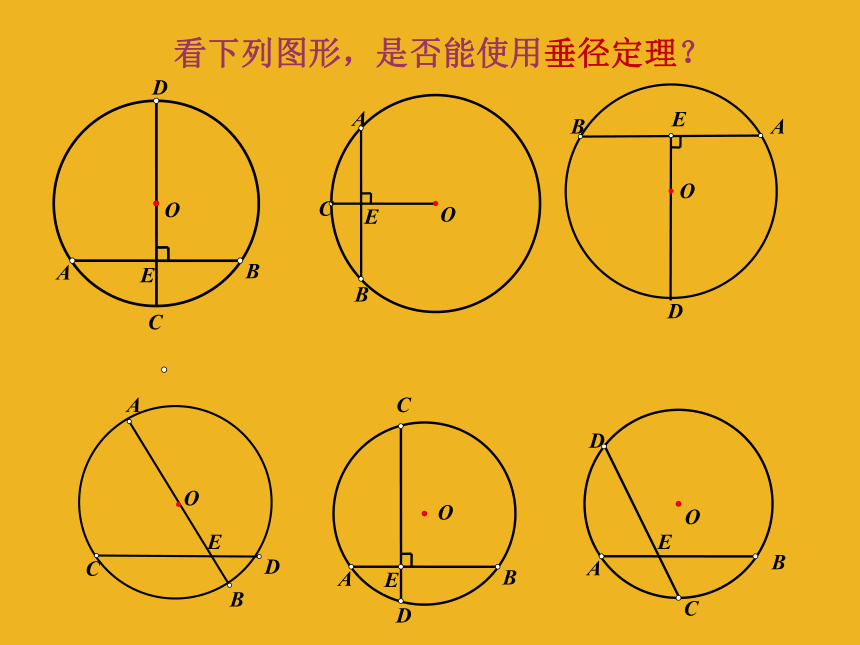
看下列图形,是否能使用垂径定理?
E
A
B
C
D
E
O
A
B
D
C
E
O
C
D
A
B
O
例1
如图,已知,以点O为圆心的两个圆中,大圆的弦AB交小圆于C、D两点.
求证:AC=BD
.
垂径定理的应用
问1:大圆的弦AB
交小圆于C
、
D
两点的含义是什么?
问2:这两个圆叫什么圆?
同心圆
B
D
A
O
C
CD是小圆的弦
例1
如图,已知,以点O为圆心的两个圆中,大圆的弦AB交小圆于C、D两点.
求证:AC=BD
.
垂径定理的应用
过圆心O作OH⊥AB,垂足为点H.
由垂径定理,得AH=BH,
同理:CH=DH,
∴AH-CH=BH-DH,
即AC=BD
B
D
A
O
C
H
证明:
37.4
7.2
例题2
石拱桥的桥拱是圆弧形,它的跨度(弧所对的弦的长)为37.4m,拱高(弧的中点到弦的距离,也叫弓形高)为7.2m.求桥拱所在圆的半径长(精确到0.1m).
R
R-7.2
根据题意,画出图形
O
A
B
D
C
跨度指的是什么?
拱高指的是什么?
如何求半径?
例题2
石拱桥的桥拱是圆弧形,它的跨度(弧所对的弦的长)为37.4m,拱高(弧的中点到弦的距离,也叫弓形高)为7.2m.求桥拱所在圆的半径长(精确到0.1m).
37.4
7.2
R
R-7.2
O
A
B
D
C
解:如图,用弧AB表示桥拱,O为圆心,联结AB,过圆心O作半径OC垂直于弦AB,垂足为点D.根据垂经定理可知D是AB的中点,C是弧AB的中点,则CD是拱高。
由题意得AB=37.4米,CD=7.2米,得
在Rt△AOD中,由勾股定理得
设半径为R,
则OD=R-7.2.
解得
R≈27.9(m).
答:赵州桥的桥拱半径约为27.9m.
1、如图,已知⊙O的弦AB长为10,半径长R为7,OC是弦AB的弦心距,求OC的长.
书13页练习
C
B
O
A
解:联结AO.
∵OC
⊥AB,O为圆心,
∴AC=
AB=
×10=5.
在Rt
△AOC中,由勾股定理得
OC=
答:OC的长为
.
添加半径是常作的辅助线.
2、已知⊙O的半径长为50cm,弦AB长50cm,
求:(1)点O到AB的距离;(2)∠AOB的大小.
解:过圆心O作OD⊥AB,D为垂足,联OA,OB.
∴AD=
AB=
×50=25.
在Rt
△AOD中,由勾股定理得
OD=
.
答:点O到AB的距离为
厘米,∠AOB=60°.
∵AO=BO=AB=50,
∴△AOB是等边三角形,
∴∠AOB=60°.
B
A
O
D
也可用锐角三角比的知识来求∠AOB.
3、如图,已知⊙O的半径OC垂直于弦AB,
垂足为点D,AD长2厘米,AB长5厘米,
求:(1)AB的长;(2)AC的长.
D
C
B
O
A
⌒
⌒
解:联结AO.
∵OD⊥AB,O为圆心,
∴AB=2AD=2×2=4.
∴
AC=
AB=
×5=2.5
⌒
⌒
⌒
答:AB的长为4厘米,AC为2.5厘米.
4、如图,已知P是⊙O内一点,画一条弦AB,使AB经过点P,并且AP=PB.
C
O
P
∴弦AB为所求.
想一想:作图的依据是什么?
B
A
总结归纳:
.
A
B
O
1、圆的轴对称性:圆是轴对称图形,任意一条直径所在的直线都是它的对称轴.
2、垂径定理:垂直于弦的直径平分弦且平分这条弦所对的弧.
3、常添辅助线:添加半径、过圆心作垂线等构造直角三角形.
本节课你有哪些收获?
练习册:P5
习题27.3(1)
布置作业:
8cm
1.半径为4cm的⊙O中,弦AB=4cm,
那么圆心O到弦AB的距离是
。
2.⊙O的直径为10cm,圆心O到弦AB的
距离为3cm,则弦AB的长是
。
3.半径为2cm的圆中,过半径中点且
垂直于这条半径的弦长是
。
补充练习
1
A
B
O
E
A
B
O
E
O
A
B
E
1.如图,在⊙O中,弦AB的长为8cm,圆心到AB的距离为3cm,则⊙O的半径为
.
·
A
B
O
∟
C
5cm
3
4
2.弓形的弦长AB为24cm,弓形的高CD为8cm,则这弓形所在圆的半径为 .
13cm
1题
2题
12
8
补充练习
2
赵州石拱桥
一千三百多年前,我国隋代建造的赵州石拱桥的桥拱是圆弧形,它的跨度(弧所对的弦的长)为37.4米,
拱高(弧的中点到弦的距离,也叫弓形高)为7.2米.
你会求桥拱所在圆的半径长吗?
§27.3
垂径定理(1)
将圆形纸片沿着直径所在的直线翻折,
新课探究
问1:能观察到什么?
问2:说明什么?
直径两侧的两个半圆互相重合.
圆是轴对称图形,任意一条直径所在的直线都是它的对称轴.
·
如图
CD
是⊙O的直径,
AB是⊙O的弦,CD⊥AB,垂足为M.
(1)利用圆是轴对称图形的性质,你能发现图中有哪些相等
的线段和弧?
(2)你能用推理的方法来证明吗?
新课探究
证明:分别联结OA、OB.
∵OA=OB
,OM
⊥AB,
又∵CD是⊙O的直径,
AM=BM,
⌒
⌒
AC
=BC,
⌒
⌒
AD
=BD.
∴CAD=CBA,即AD+AC=BD=BC,
∴AM=BM;
∠AOD=
∠BOD,AD=BD,
∴AC=BC.
·
O
A
B
C
M
D
B
C
A
M
O
.
D
总结:
垂径定理:
如果圆的一条直径垂直于一条弦,那么这条直径平分这条弦并且平分这条弦所对的弧。
CD为⊙O的直径
CD⊥AB
条件
结论
⌒
⌒
⌒
⌒
AM=BM
AC=BC
AD=BD
结论中“平分弦所对的弧”包括弦所对的劣弧和优弧。
条件“圆的直径垂直于弦”也可表述为“圆的半径垂直于弦”或“圆心到弦的垂线段”,实质是指“一条过圆心的直线(或直线部分)与圆的一条弦具有垂直关系”
简述为:垂直于弦的直径平分弦且平分这条弦所对的弧.
垂径定理的符号语言
●O
A
B
C
D
M└
CD⊥AB,
∵
CD过圆心,
∴AM=BM,
⌒
⌒
AC
=BC,
⌒
⌒
AD
=BD(垂径定理)
E
O
A
B
D
C
E
O
A
B
C
O
B
A
E
D
看下列图形,是否能使用垂径定理?
E
A
B
C
D
E
O
A
B
D
C
E
O
C
D
A
B
O
例1
如图,已知,以点O为圆心的两个圆中,大圆的弦AB交小圆于C、D两点.
求证:AC=BD
.
垂径定理的应用
问1:大圆的弦AB
交小圆于C
、
D
两点的含义是什么?
问2:这两个圆叫什么圆?
同心圆
B
D
A
O
C
CD是小圆的弦
例1
如图,已知,以点O为圆心的两个圆中,大圆的弦AB交小圆于C、D两点.
求证:AC=BD
.
垂径定理的应用
过圆心O作OH⊥AB,垂足为点H.
由垂径定理,得AH=BH,
同理:CH=DH,
∴AH-CH=BH-DH,
即AC=BD
B
D
A
O
C
H
证明:
37.4
7.2
例题2
石拱桥的桥拱是圆弧形,它的跨度(弧所对的弦的长)为37.4m,拱高(弧的中点到弦的距离,也叫弓形高)为7.2m.求桥拱所在圆的半径长(精确到0.1m).
R
R-7.2
根据题意,画出图形
O
A
B
D
C
跨度指的是什么?
拱高指的是什么?
如何求半径?
例题2
石拱桥的桥拱是圆弧形,它的跨度(弧所对的弦的长)为37.4m,拱高(弧的中点到弦的距离,也叫弓形高)为7.2m.求桥拱所在圆的半径长(精确到0.1m).
37.4
7.2
R
R-7.2
O
A
B
D
C
解:如图,用弧AB表示桥拱,O为圆心,联结AB,过圆心O作半径OC垂直于弦AB,垂足为点D.根据垂经定理可知D是AB的中点,C是弧AB的中点,则CD是拱高。
由题意得AB=37.4米,CD=7.2米,得
在Rt△AOD中,由勾股定理得
设半径为R,
则OD=R-7.2.
解得
R≈27.9(m).
答:赵州桥的桥拱半径约为27.9m.
1、如图,已知⊙O的弦AB长为10,半径长R为7,OC是弦AB的弦心距,求OC的长.
书13页练习
C
B
O
A
解:联结AO.
∵OC
⊥AB,O为圆心,
∴AC=
AB=
×10=5.
在Rt
△AOC中,由勾股定理得
OC=
答:OC的长为
.
添加半径是常作的辅助线.
2、已知⊙O的半径长为50cm,弦AB长50cm,
求:(1)点O到AB的距离;(2)∠AOB的大小.
解:过圆心O作OD⊥AB,D为垂足,联OA,OB.
∴AD=
AB=
×50=25.
在Rt
△AOD中,由勾股定理得
OD=
.
答:点O到AB的距离为
厘米,∠AOB=60°.
∵AO=BO=AB=50,
∴△AOB是等边三角形,
∴∠AOB=60°.
B
A
O
D
也可用锐角三角比的知识来求∠AOB.
3、如图,已知⊙O的半径OC垂直于弦AB,
垂足为点D,AD长2厘米,AB长5厘米,
求:(1)AB的长;(2)AC的长.
D
C
B
O
A
⌒
⌒
解:联结AO.
∵OD⊥AB,O为圆心,
∴AB=2AD=2×2=4.
∴
AC=
AB=
×5=2.5
⌒
⌒
⌒
答:AB的长为4厘米,AC为2.5厘米.
4、如图,已知P是⊙O内一点,画一条弦AB,使AB经过点P,并且AP=PB.
C
O
P
∴弦AB为所求.
想一想:作图的依据是什么?
B
A
总结归纳:
.
A
B
O
1、圆的轴对称性:圆是轴对称图形,任意一条直径所在的直线都是它的对称轴.
2、垂径定理:垂直于弦的直径平分弦且平分这条弦所对的弧.
3、常添辅助线:添加半径、过圆心作垂线等构造直角三角形.
本节课你有哪些收获?
练习册:P5
习题27.3(1)
布置作业:
8cm
1.半径为4cm的⊙O中,弦AB=4cm,
那么圆心O到弦AB的距离是
。
2.⊙O的直径为10cm,圆心O到弦AB的
距离为3cm,则弦AB的长是
。
3.半径为2cm的圆中,过半径中点且
垂直于这条半径的弦长是
。
补充练习
1
A
B
O
E
A
B
O
E
O
A
B
E
1.如图,在⊙O中,弦AB的长为8cm,圆心到AB的距离为3cm,则⊙O的半径为
.
·
A
B
O
∟
C
5cm
3
4
2.弓形的弦长AB为24cm,弓形的高CD为8cm,则这弓形所在圆的半径为 .
13cm
1题
2题
12
8
补充练习
2
