人教版九年级数学上册 数学活动:三角点阵中前n行的点数计算-1教学设计
文档属性
| 名称 | 人教版九年级数学上册 数学活动:三角点阵中前n行的点数计算-1教学设计 |
|
|
| 格式 | zip | ||
| 文件大小 | 94.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-12-26 00:00:00 | ||
图片预览



文档简介
课程基本信息
课题
数学活动:三角点阵中前n行的点数计算
教科书
书名:
《数学》九年级上册
出版社:人民教育出版社
出版日期:
2014
年3
月
教学目标
教学目标::
通过观察三角点阵,探究发现三角点阵中前
n
行的点数规律,并能用于计算.
运用一元二次方程的知识探索三角点阵中前n行的点数和的计算公式.
掌握从特殊到一般的分析问题的方法,建立数学模型解决问题.
教学重点:探索并运用三角点阵中前n行的点数和的计算公式
教学难点:探索并运用三角点阵中前n行的点数和的计算公式
时间
教学环节
教学过程
2分钟
活动1
问题引入
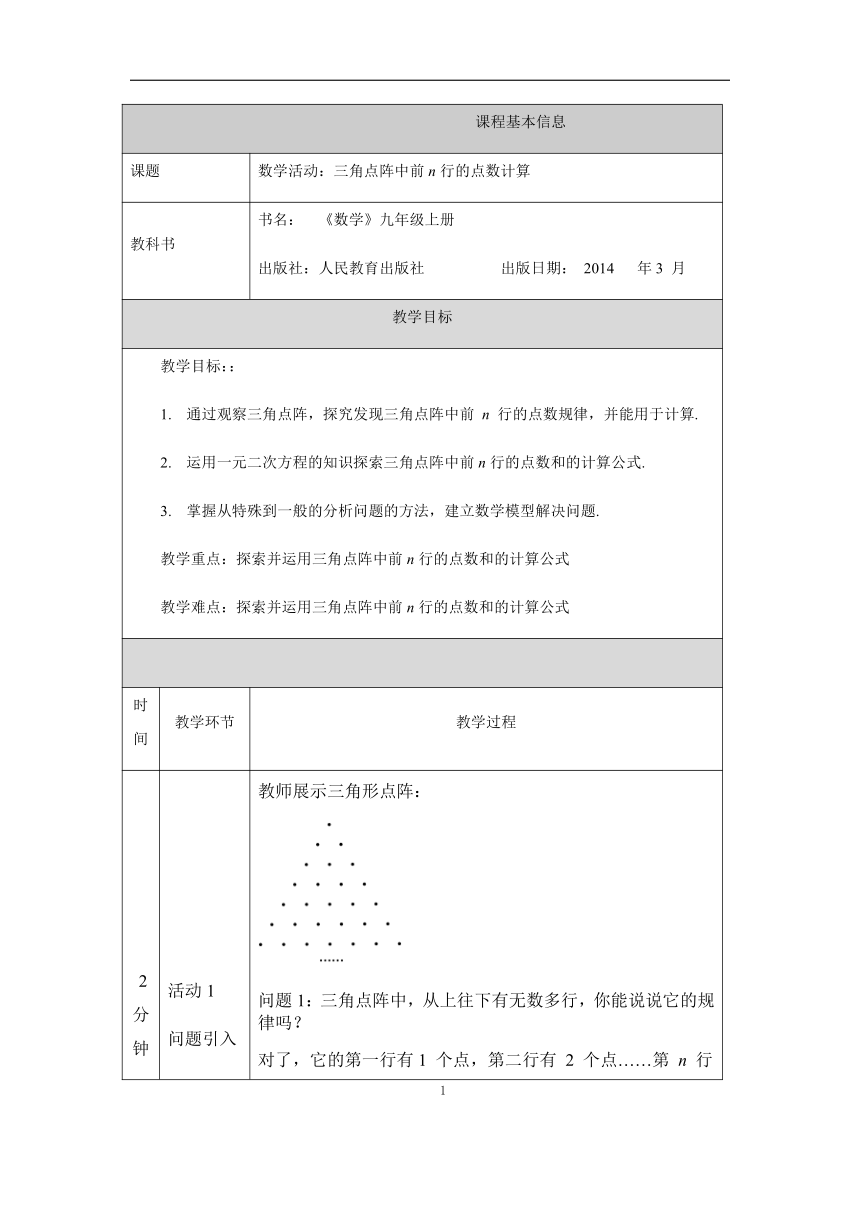
教师展示三角形点阵:
问题1:三角点阵中,从上往下有无数多行,你能说说它的规律吗?
对了,它的第一行有1
个点,第二行有
2
个点……第
n
行有
n
个点。
问题2:前4行的点数和是多少?
通过“逐个数”的方式,我们可以得到前四行的点数和是10,当然我们也可以通过这种方式得到前5行,前6行或者任意前几行的点数和,不过我们也发现当n逐渐变大,点数和越来越大,数起来就越来越麻烦了.
10分钟
活动2
探索规律
问题3:你能发现300是前多少行的点数的和吗?
我们是不是可以一行一行的加,一直加到点数和为300?
很明显我们只要列出算式:
这样由上而下地逐行相加其点数,就可以得到答案
也就是说,前24行的点数和为300。但是很明显的,这样寻找答案要花费较多时间,能有更快捷的方法来解决这个问题吗?
你想到了吗?我们只要能够推导出三角点阵中前n行的点数公式就可以借助方程解决这个问题了。
基于我们之前对于三角点阵的分析,它前n行的点数和应该这样计算:
我们发现:
这样我们只要能够确定这n个数相加有多少对和为(n+1)的数就可以啦!
如果n为偶数,一共有对,所以和为
如果n为奇数,n项不能均分成两部分,最中间的数是,这样还剩下n-1个数,n-1为偶数,也就是有对和为(n+1)的数,所以这n个数的总和为,整理得,得到.发现和n为偶数的情况得到的结果是一样的,也就是说无论n为奇数还是偶数都有.
整理得,得到.
也就是说无论n为奇数还是偶数都有
这样我们就得到了三角点阵前n行的点数和公式.
除了分类讨论之外,我们为了能够实现的“首尾相加”,还可以考虑把和写成倒序形式,我们不妨设记为方程①,再将这个等式的右边改写成倒序相加的形式,记为方程②,将这两个方程相加,得到等式右边有n个(n+1)做和,所以得到解得也可以得到的值是.这样做是不是更快捷了?
也有同学会提出问题,这样做倒序相加,再结合三角点阵的背景,不就是将一个正立的三角和一个倒立的三角拼在一起吗?能不能直接利用到图形特征来求呢?我们来一起看一看
以前7行为例,如果我们将2个三角点阵如图放置
我们可以把它们组合成一个平行四边形
把其中一个点阵进行移动,我们可以把它们组合成一个平行四边形点阵,此时可以用平行四边形的面积公式算得平行四边形点阵的点数和为,也就是两个7行的三角点阵的点数和为,那么一个7行的三角形点阵的点数和为.
活动3
建立方程
解决问题
我们再回到问题3:你能发现300是前多少行的点数的和吗?
将方程:
转化为:
整理得:
解得:
由实际意义得:
即三角形点阵中前24行的点数和为300.
活动4
巩固提高
拓展延伸
通过刚才的探索,我们发现,得到自然数的前n项和的公式后,可以建立一元二次方程,“一劳永逸”的解决类似的问题,比如:
问题4:三角点阵中前n行的和能是600吗?如果能,求出n;如果不能,请说明理由.
我们可以直接依题意列出方程:
整理得:
计算
发现尽管此方程有两个不等实根,但是由于不是完全平方数,所以得不到正整数根,不符合题意.
所以三角点阵中前n行的和不可能是600.
如果三角形各行的点数换了呢?那我们推得的公式就不适用了,如何解决?我们来看问题5,
问题5:如果把三角形点阵中各行的点数依次换为
2,4,6,…,2n,…,你能探究出前n行的点数和满足什么规律吗?这个三角点阵中前n行的点数和能是600吗?如果能,求出n;如果不能,请说明理由.
根据题意列出方程:
变形为:
由之前推导出的公式,可得:
根据实际意义,解得:
活动5:
本课小结
本节课我们在三角点阵前n行的点数计算的探索过程中,通过观察算式特征和图形的特征,发现了规律,得到了公式,将繁琐的计算转化为简洁的一元二次方程,从而解决了问题。这个过程体现了利用已有的知识和熟悉的方法来解决不熟悉的问题,这也正是解决数学问题的最常用的方法.
6
课题
数学活动:三角点阵中前n行的点数计算
教科书
书名:
《数学》九年级上册
出版社:人民教育出版社
出版日期:
2014
年3
月
教学目标
教学目标::
通过观察三角点阵,探究发现三角点阵中前
n
行的点数规律,并能用于计算.
运用一元二次方程的知识探索三角点阵中前n行的点数和的计算公式.
掌握从特殊到一般的分析问题的方法,建立数学模型解决问题.
教学重点:探索并运用三角点阵中前n行的点数和的计算公式
教学难点:探索并运用三角点阵中前n行的点数和的计算公式
时间
教学环节
教学过程
2分钟
活动1
问题引入
教师展示三角形点阵:
问题1:三角点阵中,从上往下有无数多行,你能说说它的规律吗?
对了,它的第一行有1
个点,第二行有
2
个点……第
n
行有
n
个点。
问题2:前4行的点数和是多少?
通过“逐个数”的方式,我们可以得到前四行的点数和是10,当然我们也可以通过这种方式得到前5行,前6行或者任意前几行的点数和,不过我们也发现当n逐渐变大,点数和越来越大,数起来就越来越麻烦了.
10分钟
活动2
探索规律
问题3:你能发现300是前多少行的点数的和吗?
我们是不是可以一行一行的加,一直加到点数和为300?
很明显我们只要列出算式:
这样由上而下地逐行相加其点数,就可以得到答案
也就是说,前24行的点数和为300。但是很明显的,这样寻找答案要花费较多时间,能有更快捷的方法来解决这个问题吗?
你想到了吗?我们只要能够推导出三角点阵中前n行的点数公式就可以借助方程解决这个问题了。
基于我们之前对于三角点阵的分析,它前n行的点数和应该这样计算:
我们发现:
这样我们只要能够确定这n个数相加有多少对和为(n+1)的数就可以啦!
如果n为偶数,一共有对,所以和为
如果n为奇数,n项不能均分成两部分,最中间的数是,这样还剩下n-1个数,n-1为偶数,也就是有对和为(n+1)的数,所以这n个数的总和为,整理得,得到.发现和n为偶数的情况得到的结果是一样的,也就是说无论n为奇数还是偶数都有.
整理得,得到.
也就是说无论n为奇数还是偶数都有
这样我们就得到了三角点阵前n行的点数和公式.
除了分类讨论之外,我们为了能够实现的“首尾相加”,还可以考虑把和写成倒序形式,我们不妨设记为方程①,再将这个等式的右边改写成倒序相加的形式,记为方程②,将这两个方程相加,得到等式右边有n个(n+1)做和,所以得到解得也可以得到的值是.这样做是不是更快捷了?
也有同学会提出问题,这样做倒序相加,再结合三角点阵的背景,不就是将一个正立的三角和一个倒立的三角拼在一起吗?能不能直接利用到图形特征来求呢?我们来一起看一看
以前7行为例,如果我们将2个三角点阵如图放置
我们可以把它们组合成一个平行四边形
把其中一个点阵进行移动,我们可以把它们组合成一个平行四边形点阵,此时可以用平行四边形的面积公式算得平行四边形点阵的点数和为,也就是两个7行的三角点阵的点数和为,那么一个7行的三角形点阵的点数和为.
活动3
建立方程
解决问题
我们再回到问题3:你能发现300是前多少行的点数的和吗?
将方程:
转化为:
整理得:
解得:
由实际意义得:
即三角形点阵中前24行的点数和为300.
活动4
巩固提高
拓展延伸
通过刚才的探索,我们发现,得到自然数的前n项和的公式后,可以建立一元二次方程,“一劳永逸”的解决类似的问题,比如:
问题4:三角点阵中前n行的和能是600吗?如果能,求出n;如果不能,请说明理由.
我们可以直接依题意列出方程:
整理得:
计算
发现尽管此方程有两个不等实根,但是由于不是完全平方数,所以得不到正整数根,不符合题意.
所以三角点阵中前n行的和不可能是600.
如果三角形各行的点数换了呢?那我们推得的公式就不适用了,如何解决?我们来看问题5,
问题5:如果把三角形点阵中各行的点数依次换为
2,4,6,…,2n,…,你能探究出前n行的点数和满足什么规律吗?这个三角点阵中前n行的点数和能是600吗?如果能,求出n;如果不能,请说明理由.
根据题意列出方程:
变形为:
由之前推导出的公式,可得:
根据实际意义,解得:
活动5:
本课小结
本节课我们在三角点阵前n行的点数计算的探索过程中,通过观察算式特征和图形的特征,发现了规律,得到了公式,将繁琐的计算转化为简洁的一元二次方程,从而解决了问题。这个过程体现了利用已有的知识和熟悉的方法来解决不熟悉的问题,这也正是解决数学问题的最常用的方法.
6
同课章节目录
