人教版数学九年级上册:直线和圆的位置关系 课件(共14张PPT)
文档属性
| 名称 | 人教版数学九年级上册:直线和圆的位置关系 课件(共14张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 462.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-12-25 00:00:00 | ||
图片预览

文档简介
直线和圆的位置关系
?1
?
P
A
B
C
如图,直线?1外有一点P,在直线?1上分别取A,B,C三点并连接。哪条线段是P到?1的距离?
?
点到直线的距离指的是什么?
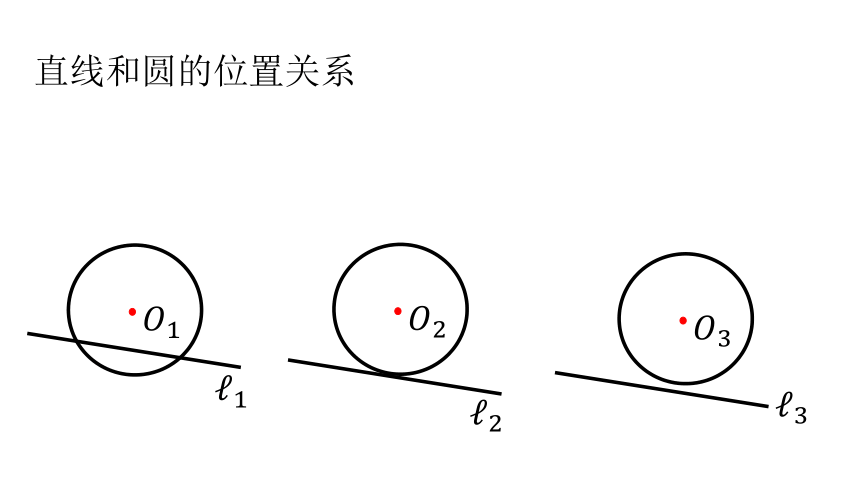
直线和圆的位置关系
?1
?
????1
?
?2
?
????2
?
?3
?
????3
?
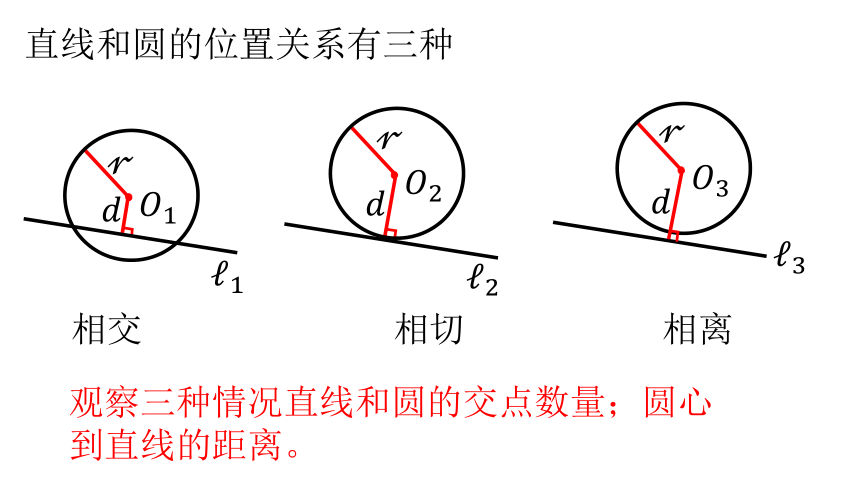
直线和圆的位置关系有三种
?1
?
????1
?
?2
?
????2
?
?3
?
????3
?
相交 相切 相离
????
?
????
?
????
?
????
?
????
?
????
?
观察三种情况直线和圆的交点数量;圆心到直线的距离。
?1
?
????1
?
?2
?
????2
?
?3
?
????3
?
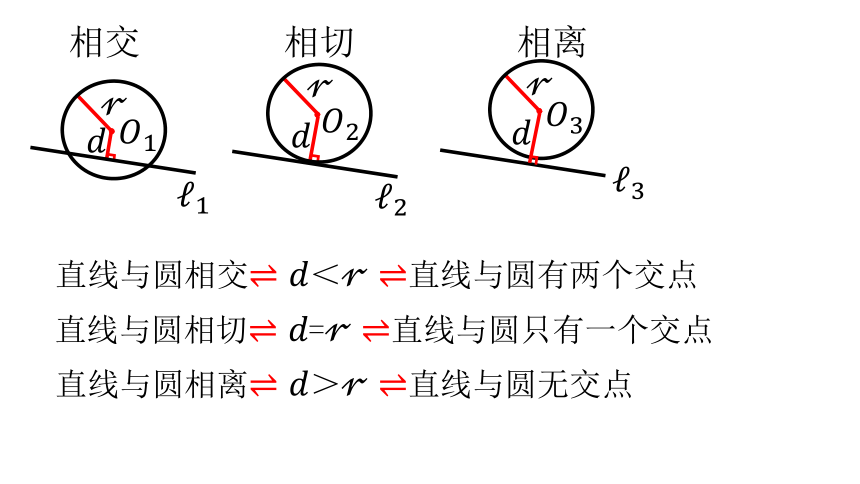
相交 相切 相离
????
?
????
?
????
?
????
?
????
?
????
?
直线与圆相交?????<?????直线与圆有两个交点
?
直线与圆相切?????=?????直线与圆只有一个交点
?
直线与圆相离?????>?????直线与圆无交点
?
A
O
B
P
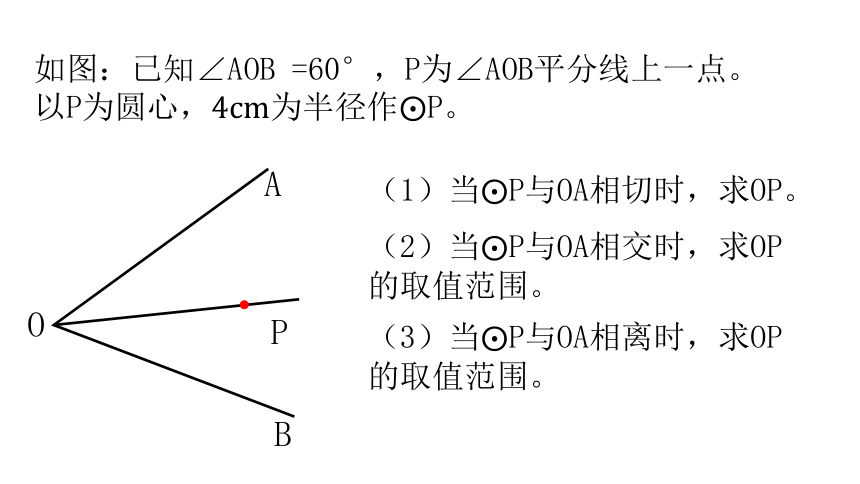
如图:已知∠AOB =60°,P为∠AOB平分线上一点。以P为圆心,4cm为半径作?P。
?
(1)当?P与OA相切时,求OP。
?
(2)当?P与OA相交时,求OP的取值范围。
?
(3)当?P与OA相离时,求OP的取值范围。
?
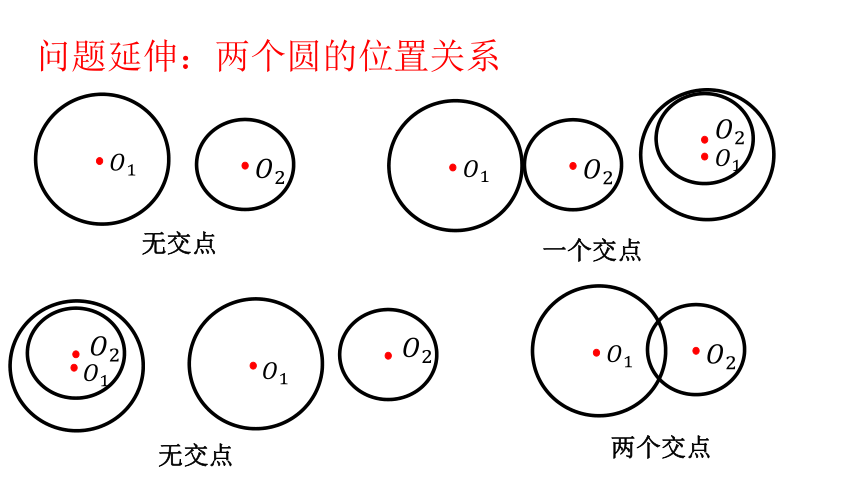
问题延伸:两个圆的位置关系
????1
?
????2
?
????1
?
????2
?
????1
?
????2
?
无交点
????1
?
????2
?
一个交点
两个交点
无交点
????1
?
????2
?
????1
?
????2
?
????1
?
????2
?
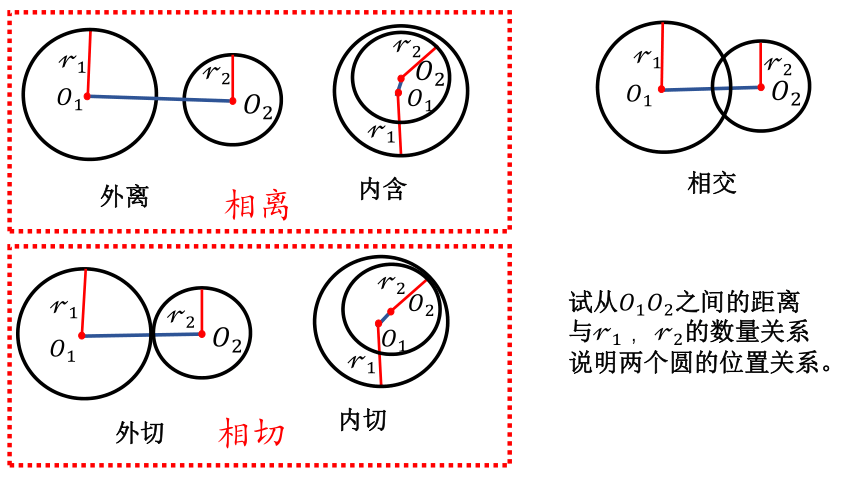
外离
????1
?
????2
?
????1
?
????2
?
外切
????1
?
????2
?
????1
?
????2
?
内含
相离
????1
?
????2
?
????1
?
????2
?
相交
????1
?
????2
?
试从????1????2之间的距离与????1 ,????2的数量关系说明两个圆的位置关系。
?
????1
?
????2
?
内切
????1
?
????2
?
相切
O
P
?1
?
切线的判定和性质
如图:已知直线?1为?????的切线。
思考:
1.OP的长度与?????的半径的关系。
2.点P与?????的位置关系,OP是什 么?
3.OP⊥ ?1吗?是否一定?
?
切线的定义:
切线的定义:经过半径的外端且垂直于这条半径的直线是圆的切线。
切线的两大要素:
1.经过半径的外端。
2.垂直于这条半径的直线是圆的切线。
两个要素缺一不可,缺一则不存在切线;都满足则为切线。
1.如图:P为?????上一点,直线?1经过点P,若直线?1要成为?????的切线,需要满足什么条件?要如何做?
?
O
P
?1
?
2.如图所示,以△ABC的边AB为直径做?O,点C在?O上,BD是?O的弦,∠A=∠CBD,过点C作CF⊥AB于点F,交BD于点G,过点C作CE∥BD交AB延长线于点E。
(1)求证:CE是?O的切线。
(2)求证:CG=BG
(3)若∠DBA=30°,CG=4,求BE的长。
?
A
B
C
D
F
G
E
O
3.如图:过 ?????的圆心O作OP⊥ ?1于点P,若直线?1要成为?????的切线,需要满足什么条件?
?
O
P
?1
?
4.如图:在梯形ABCD中,AD∥BC,∠D=90°;AD+BC=AB,以AB为直径作?O。
求证: ?O与CD相切。
?
A
O
B
C
D
证明一条直线是圆的切线要看是否满足这两个条件:
1.经过半径的外端。
2.垂直于这条半径的直线是圆的切线。
方法:
1.是半径?证垂直
2.已垂直?证半径
?1
?
P
A
B
C
如图,直线?1外有一点P,在直线?1上分别取A,B,C三点并连接。哪条线段是P到?1的距离?
?
点到直线的距离指的是什么?
直线和圆的位置关系
?1
?
????1
?
?2
?
????2
?
?3
?
????3
?
直线和圆的位置关系有三种
?1
?
????1
?
?2
?
????2
?
?3
?
????3
?
相交 相切 相离
????
?
????
?
????
?
????
?
????
?
????
?
观察三种情况直线和圆的交点数量;圆心到直线的距离。
?1
?
????1
?
?2
?
????2
?
?3
?
????3
?
相交 相切 相离
????
?
????
?
????
?
????
?
????
?
????
?
直线与圆相交?????<?????直线与圆有两个交点
?
直线与圆相切?????=?????直线与圆只有一个交点
?
直线与圆相离?????>?????直线与圆无交点
?
A
O
B
P
如图:已知∠AOB =60°,P为∠AOB平分线上一点。以P为圆心,4cm为半径作?P。
?
(1)当?P与OA相切时,求OP。
?
(2)当?P与OA相交时,求OP的取值范围。
?
(3)当?P与OA相离时,求OP的取值范围。
?
问题延伸:两个圆的位置关系
????1
?
????2
?
????1
?
????2
?
????1
?
????2
?
无交点
????1
?
????2
?
一个交点
两个交点
无交点
????1
?
????2
?
????1
?
????2
?
????1
?
????2
?
外离
????1
?
????2
?
????1
?
????2
?
外切
????1
?
????2
?
????1
?
????2
?
内含
相离
????1
?
????2
?
????1
?
????2
?
相交
????1
?
????2
?
试从????1????2之间的距离与????1 ,????2的数量关系说明两个圆的位置关系。
?
????1
?
????2
?
内切
????1
?
????2
?
相切
O
P
?1
?
切线的判定和性质
如图:已知直线?1为?????的切线。
思考:
1.OP的长度与?????的半径的关系。
2.点P与?????的位置关系,OP是什 么?
3.OP⊥ ?1吗?是否一定?
?
切线的定义:
切线的定义:经过半径的外端且垂直于这条半径的直线是圆的切线。
切线的两大要素:
1.经过半径的外端。
2.垂直于这条半径的直线是圆的切线。
两个要素缺一不可,缺一则不存在切线;都满足则为切线。
1.如图:P为?????上一点,直线?1经过点P,若直线?1要成为?????的切线,需要满足什么条件?要如何做?
?
O
P
?1
?
2.如图所示,以△ABC的边AB为直径做?O,点C在?O上,BD是?O的弦,∠A=∠CBD,过点C作CF⊥AB于点F,交BD于点G,过点C作CE∥BD交AB延长线于点E。
(1)求证:CE是?O的切线。
(2)求证:CG=BG
(3)若∠DBA=30°,CG=4,求BE的长。
?
A
B
C
D
F
G
E
O
3.如图:过 ?????的圆心O作OP⊥ ?1于点P,若直线?1要成为?????的切线,需要满足什么条件?
?
O
P
?1
?
4.如图:在梯形ABCD中,AD∥BC,∠D=90°;AD+BC=AB,以AB为直径作?O。
求证: ?O与CD相切。
?
A
O
B
C
D
证明一条直线是圆的切线要看是否满足这两个条件:
1.经过半径的外端。
2.垂直于这条半径的直线是圆的切线。
方法:
1.是半径?证垂直
2.已垂直?证半径
同课章节目录
