人教版数学九年级上册:圆与圆的位置关系 课件(共36张PPT)
文档属性
| 名称 | 人教版数学九年级上册:圆与圆的位置关系 课件(共36张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 234.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-12-25 18:49:20 | ||
图片预览








文档简介
圆
圆
与
的
位
置
关
系
圆与圆的位置关系
.
o
.
.
一:点与圆的位置关系:
(2)点在圆上
(1)点在圆内
(3)点在圆外
.
相离
相切
相交
二:直线与圆的位置关系:
复习巩固
探究:
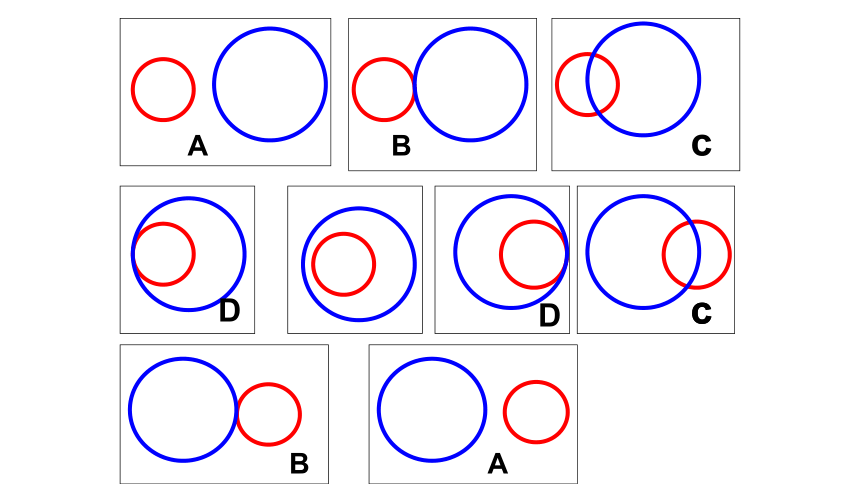
圆和圆有哪几种位置关系?
认真观察
观察结果
A
A
B
B
c
c
c
D
D
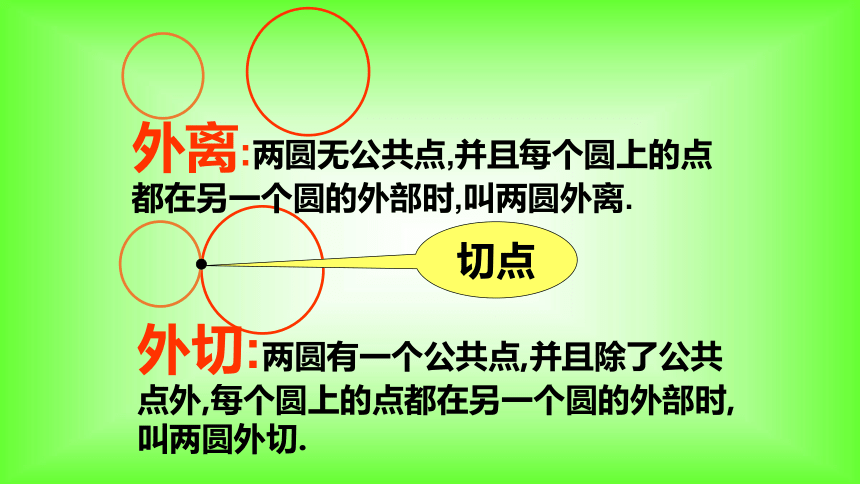
外离:两圆无公共点,并且每个圆上的点都在另一个圆的外部时,叫两圆外离.
外切:两圆有一个公共点,并且除了公共点外,每个圆上的点都在另一个圆的外部时,叫两圆外切.
切点
切点
相交:两圆有两个公共点时,叫两圆相交.
内切:两圆有一个公共点,并且除了公共点外,一个圆上的点都在另一个圆的内部时,叫两圆内切.
内含:两圆无公共点,并且一个圆上的点都在另一个圆的内部时,叫两圆内含.
特 例
.O
同心圆
圆
和
圆
的
位
置
关
系
1、外 离
4、内 切
5、相 交
3、外 切
2、内 含
没有公共点
相 离
一个公共点
相切
两个公共点
相交
圆与圆的位置关系
一、点与圆的位置关系:
(2)点在圆上
(1)点在圆内
(3)点在圆外
二、直线与圆的位置关系:
d<r
d=r
d>r
相离
相切
相交
d>r
d=r
d回顾:
能否类比点与圆的位置关系和直线与圆的位置关系,也能用d和r之间的数量关系来反应圆与圆的位置关系?
圆心距:两圆心之间的距离叫圆心距.(用d表示)
O
O
B
A
1
2
d
d
点与圆的位置关系: d表示点到圆心的距离
直线与圆的位置关系: d表示点到直线的距离
o1
o2
R
r
d
d>R+r
精彩源于发现
外 离
R
r
d
o1
o2
d=R+r
T
外 切
o1
o2
r
R
d
d=R-r (R>r)
T
内 切
o1
o2
d
R
r
相 交
R-r (R>r)
d=R+r
o1
o2
o1
o2
o1
o2
d=R-r
R-rr)
O
O1
O2
0≤dr)
内 含
d=0
d=R-r
O2
O1
1、外 离
4、内 切
5、相 交
3、外 切
2、内 含
圆与圆的位置关系
d>R+r
d=R+r
R-rr)
0≤dr)
d=R-r (R>r)
两圆位置关系的性质与判定:
0
R―r
R+r
同心圆
内含
外离
外切
相交
内切
位 置 关 系 数 字 化
d
巩固练习:
1、 ⊙O1和⊙O2的半径分别为3厘米和4厘米,
设(1) O1O2=8厘米; (2) O1O2=7厘米;
(3) O1O2=5厘米; (4) O1O2=1厘米;
(5) O1O2=0.5厘米; (6) O1和O2重合。
⊙O1和⊙O2的位置关系怎样?
(1)、外 离
(4)、内 切
(3)、相 交
(2)、外 切
(5)、内 含(同心)
2.已知两圆的半径分别为1厘米和5厘米,
(1)若两圆相交,则圆心距d的取值范围是 ;
(2)若两圆外离则d的取值范围 ;
(3)若两圆内含则d的取值范围 ;
若两圆相切则d= .
口答:(看谁答得对)
R=3 cm
R=13 cm
.
.
P
O
例题:如图⊙O的半径为5cm,点P是⊙O外一点,
OP=8cm。若以P为圆心作⊙P与⊙O相切,求⊙P的半径?
.
.
P
O
综上⊙P的半径为3cm或13cm
解:设⊙P的半径为R
(1)若⊙O与⊙P外切,
则 R =op-5=8-5
则 R =8-5
(2)若⊙O与⊙P内切,
则 R=OP+5=8,
R
5
R
5
.
.
P
O
.
P
O
练习3.两圆的半径之比为5:3,当两圆相切时,圆心距为8cm,求两圆的半径?
解:设大圆的半径为5x,小圆的半径为3x
两圆外切时:5x+3x=8 得x=1
∴两圆半径分别为5cm和3cm
两圆内切时:5x-3x=8 得x=4
∴两圆半径分别为20cm和12cm
4、定圆O的半径是4厘米,动圆P的半径是1厘米。
(1)设⊙P和⊙O相外切,那么点P与点O的距离是多少?点P可以在什么样的线上移动?
.
.
5
.
.
3
(2)设⊙P和⊙O相内切,情况怎样?
O
P
.
.
.
.
.
.
.
.
以0为圆心5cm为半径的圆上移动
以0为圆心3cm为半径的圆上移动
5.分别以1厘米、2厘米、4厘米为 半径,用圆规画圆,使他们两两外切。
6.两个半径相等的圆的位置关系有几种?
外离
外切
相交
重合
小结:
1)两圆的五种位置关系
2)用两圆的圆心距d与两圆的半径R,r的数量关系来判别两圆的位置关系
位置关系
d 和R、 r关系
交点
两圆外
两圆外切
两圆相交
两圆内切
两圆内含
两圆位置关系的性质与判定:
d>R+r
d=R+r
R?rR?r=d
R?r>d
0
1
2
1
0
已知半径均为1厘米的两圆外切,半径为2厘米,且和这两
圆都相切的圆共有 个.
5
思考题
思考题
⊙A与⊙B的半径都是1cm, ⊙A与⊙B外切于原点O(如图),
A(-1,0),B(1,0), ⊙C的半径为3cm, ⊙C与⊙A 和
⊙B都相切,
(1)这样的圆有 个;
O
A
(2)写出点C的坐标.
B
6
C1 (-3,0)
C2 (3,0)
C3 (0,15)
C4 ( 0,- 15 )
C5 (0,3)
C6 (0,- 3)
x
y
1.已知两圆的半径分别为3厘米和2厘米,若两圆没有公共点,则圆心距d的取值范围为
思考题
2. ☉A 和☉B的半径分别为6厘米和3厘米,A和B的坐标分别为(5,0)和(0,6),则两圆的位置关系是
3.分别以1厘米、2厘米、4厘米为 半径,用圆规画圆,使他们两两外切。
思考题
圆
与
的
位
置
关
系
圆与圆的位置关系
.
o
.
.
一:点与圆的位置关系:
(2)点在圆上
(1)点在圆内
(3)点在圆外
.
相离
相切
相交
二:直线与圆的位置关系:
复习巩固
探究:
圆和圆有哪几种位置关系?
认真观察
观察结果
A
A
B
B
c
c
c
D
D
外离:两圆无公共点,并且每个圆上的点都在另一个圆的外部时,叫两圆外离.
外切:两圆有一个公共点,并且除了公共点外,每个圆上的点都在另一个圆的外部时,叫两圆外切.
切点
切点
相交:两圆有两个公共点时,叫两圆相交.
内切:两圆有一个公共点,并且除了公共点外,一个圆上的点都在另一个圆的内部时,叫两圆内切.
内含:两圆无公共点,并且一个圆上的点都在另一个圆的内部时,叫两圆内含.
特 例
.O
同心圆
圆
和
圆
的
位
置
关
系
1、外 离
4、内 切
5、相 交
3、外 切
2、内 含
没有公共点
相 离
一个公共点
相切
两个公共点
相交
圆与圆的位置关系
一、点与圆的位置关系:
(2)点在圆上
(1)点在圆内
(3)点在圆外
二、直线与圆的位置关系:
d<r
d=r
d>r
相离
相切
相交
d>r
d=r
d
能否类比点与圆的位置关系和直线与圆的位置关系,也能用d和r之间的数量关系来反应圆与圆的位置关系?
圆心距:两圆心之间的距离叫圆心距.(用d表示)
O
O
B
A
1
2
d
d
点与圆的位置关系: d表示点到圆心的距离
直线与圆的位置关系: d表示点到直线的距离
o1
o2
R
r
d
d>R+r
精彩源于发现
外 离
R
r
d
o1
o2
d=R+r
T
外 切
o1
o2
r
R
d
d=R-r (R>r)
T
内 切
o1
o2
d
R
r
相 交
R-r
d=R+r
o1
o2
o1
o2
o1
o2
d=R-r
R-r
O
O1
O2
0≤d
内 含
d=0
d=R-r
O2
O1
1、外 离
4、内 切
5、相 交
3、外 切
2、内 含
圆与圆的位置关系
d>R+r
d=R+r
R-r
0≤d
d=R-r (R>r)
两圆位置关系的性质与判定:
0
R―r
R+r
同心圆
内含
外离
外切
相交
内切
位 置 关 系 数 字 化
d
巩固练习:
1、 ⊙O1和⊙O2的半径分别为3厘米和4厘米,
设(1) O1O2=8厘米; (2) O1O2=7厘米;
(3) O1O2=5厘米; (4) O1O2=1厘米;
(5) O1O2=0.5厘米; (6) O1和O2重合。
⊙O1和⊙O2的位置关系怎样?
(1)、外 离
(4)、内 切
(3)、相 交
(2)、外 切
(5)、内 含(同心)
2.已知两圆的半径分别为1厘米和5厘米,
(1)若两圆相交,则圆心距d的取值范围是 ;
(2)若两圆外离则d的取值范围 ;
(3)若两圆内含则d的取值范围 ;
若两圆相切则d= .
口答:(看谁答得对)
R=3 cm
R=13 cm
.
.
P
O
例题:如图⊙O的半径为5cm,点P是⊙O外一点,
OP=8cm。若以P为圆心作⊙P与⊙O相切,求⊙P的半径?
.
.
P
O
综上⊙P的半径为3cm或13cm
解:设⊙P的半径为R
(1)若⊙O与⊙P外切,
则 R =op-5=8-5
则 R =8-5
(2)若⊙O与⊙P内切,
则 R=OP+5=8,
R
5
R
5
.
.
P
O
.
P
O
练习3.两圆的半径之比为5:3,当两圆相切时,圆心距为8cm,求两圆的半径?
解:设大圆的半径为5x,小圆的半径为3x
两圆外切时:5x+3x=8 得x=1
∴两圆半径分别为5cm和3cm
两圆内切时:5x-3x=8 得x=4
∴两圆半径分别为20cm和12cm
4、定圆O的半径是4厘米,动圆P的半径是1厘米。
(1)设⊙P和⊙O相外切,那么点P与点O的距离是多少?点P可以在什么样的线上移动?
.
.
5
.
.
3
(2)设⊙P和⊙O相内切,情况怎样?
O
P
.
.
.
.
.
.
.
.
以0为圆心5cm为半径的圆上移动
以0为圆心3cm为半径的圆上移动
5.分别以1厘米、2厘米、4厘米为 半径,用圆规画圆,使他们两两外切。
6.两个半径相等的圆的位置关系有几种?
外离
外切
相交
重合
小结:
1)两圆的五种位置关系
2)用两圆的圆心距d与两圆的半径R,r的数量关系来判别两圆的位置关系
位置关系
d 和R、 r关系
交点
两圆外
两圆外切
两圆相交
两圆内切
两圆内含
两圆位置关系的性质与判定:
d>R+r
d=R+r
R?r
R?r>d
0
1
2
1
0
已知半径均为1厘米的两圆外切,半径为2厘米,且和这两
圆都相切的圆共有 个.
5
思考题
思考题
⊙A与⊙B的半径都是1cm, ⊙A与⊙B外切于原点O(如图),
A(-1,0),B(1,0), ⊙C的半径为3cm, ⊙C与⊙A 和
⊙B都相切,
(1)这样的圆有 个;
O
A
(2)写出点C的坐标.
B
6
C1 (-3,0)
C2 (3,0)
C3 (0,15)
C4 ( 0,- 15 )
C5 (0,3)
C6 (0,- 3)
x
y
1.已知两圆的半径分别为3厘米和2厘米,若两圆没有公共点,则圆心距d的取值范围为
思考题
2. ☉A 和☉B的半径分别为6厘米和3厘米,A和B的坐标分别为(5,0)和(0,6),则两圆的位置关系是
3.分别以1厘米、2厘米、4厘米为 半径,用圆规画圆,使他们两两外切。
思考题
同课章节目录
