沪教版(上海)初中数学八年级第一学期 19.7 直角三角形全等的判定 课件(共18张ppt)
文档属性
| 名称 | 沪教版(上海)初中数学八年级第一学期 19.7 直角三角形全等的判定 课件(共18张ppt) |

|
|
| 格式 | zip | ||
| 文件大小 | 162.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-12-25 00:00:00 | ||
图片预览



文档简介
(共18张PPT)
19.7直角三角形全等的判定
C’
C
A
B
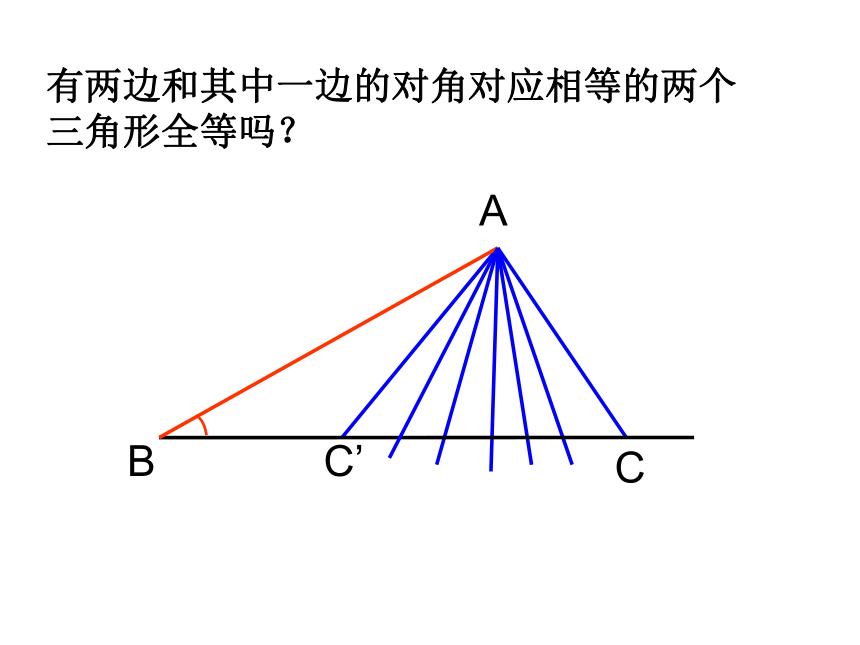
有两边和其中一边的对角对应相等的两个
三角形全等吗?
B
C’
A
B
A
C
动画演示
对于一般的三角形,“边边角”不可以证明三角形全等
如果两个直角三角形的斜边和一条直角边对应相等,那么这两个直角三角形全等。
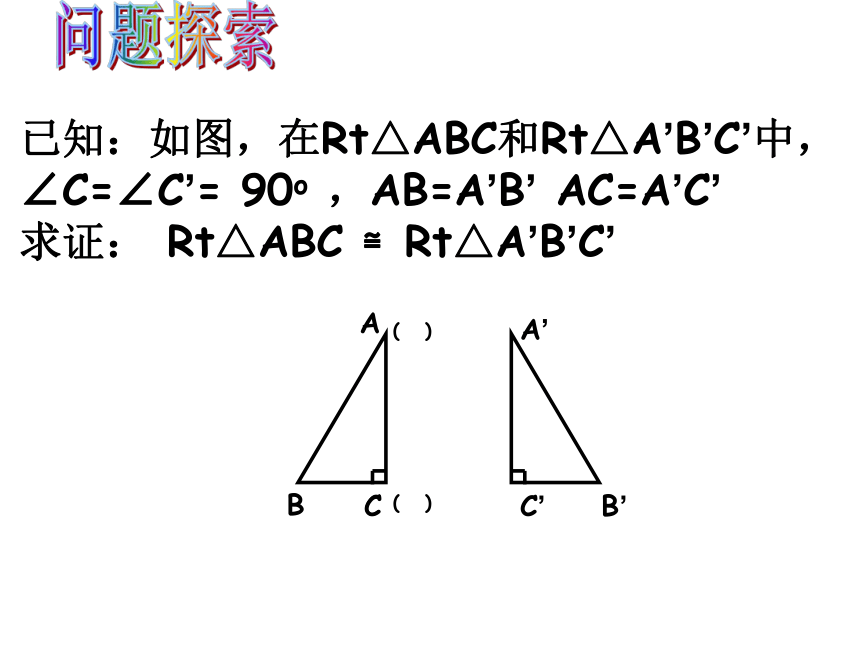
已知:如图,在Rt△ABC和Rt△A’B’C’中,∠C=∠C’=
90o
,AB=A’B’
AC=A’C’
求证:
Rt△ABC
≌Rt△A’B’C’
命题
问题探索
A’
C’
B’
A
B
C
B’
A’
C’
B
C
A
问题探索
C
(
)
(
)
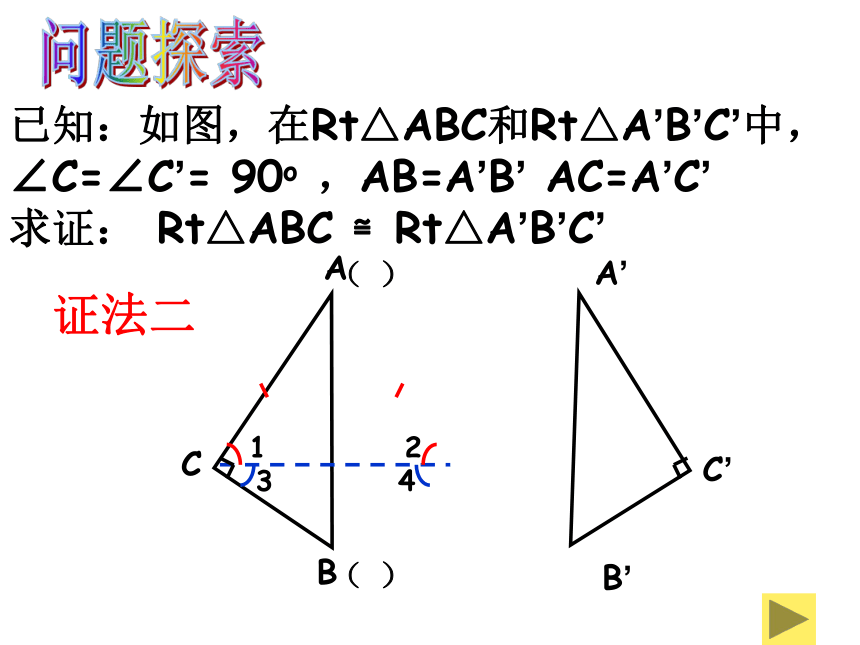
已知:如图,在Rt△ABC和Rt△A’B’C’中,∠C=∠C’=
90o
,AB=A’B’
AC=A’C’
求证:
Rt△ABC
≌Rt△A’B’C’
C
A
B
(
)
(
)
1
2
3
4
C’
B’
A’
证法二
问题探索
已知:如图,在Rt△ABC和Rt△A’B’C’中,∠C=∠C’=
90o
,AB=A’B’
AC=A’C’
求证:
Rt△ABC
≌Rt△A’B’C’
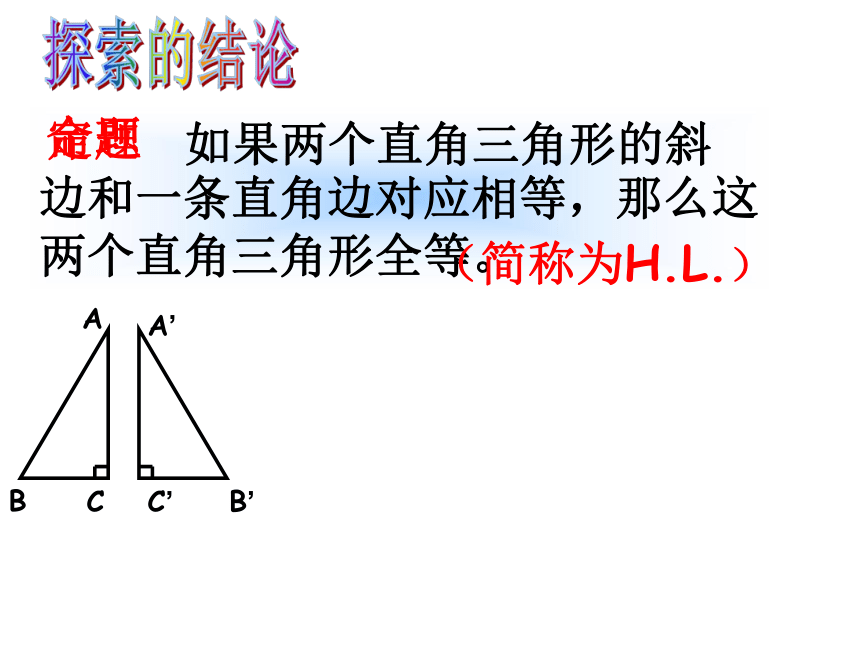
如果两个直角三角形的斜边和一条直角边对应相等,那么这两个直角三角形全等。
(简称为H.L.)
定理
命题
探索的结论
B’
A’
C’
B
C
A
(3)AB=A’B’,BC=B’C’
(
)
_____
(2)AC=A’C’,BC=B’C’
(
)
_____
如图,具有下列条件的RT△ABC
和RT△A’B’C’(其中∠C=∠C’=
90o
)是否全等?如果全等在(
)里打“√”,并在“——”上填写判定三角形全等的理由,如果不全等,在(
)里打“×”。
(1)AC=A’C’,∠A=∠A’
(
)
_____
√
√
√
A.S.A.
S.A.S.
H.L.
练一练
B’
A’
C’
B
C
A
(6)
BC=B’C’,∠A=∠A’
(
)
_____
(5)AC=A’C’,AB=A’B’
(
)
_____
练一练
如图,具有下列条件的RT△ABC
和RT△A’B’C’(其中∠C=∠C’=
90o
)是否全等?如果全等在(
)里打“√”,并在“——”上填写判定三角形全等的理由,如果不全等,在(
)里打“×”。
(4)∠A=∠A’,∠B=∠B’
(
)
_____
√
√
A.A.S.
H.L.
×
B’
A’
C’
B
C
A
例1
已知:如图,QD⊥OB,QE⊥OA,垂足分别是点D、E,且QD=QE
求证:点Q在∠AOB的平分线上
例题讲解
逆定理:在一个角的内部(包括顶点)且到角的两边距离相等的点,在这个角的平分线上
已知:如图,在△ABC中,BD⊥AC,CE⊥AB,点D、E为垂足,BD和CE相交于点F,BD=CE.
求证:三角形ABC为等腰三角形
B
A
C
O
E
D
试一试
本节我们学习了哪些什么知识?
有哪些收获、体会,
请
畅所欲言!
畅所欲言!!
畅所欲言!!!
小结
直角三角形全等的判定
一般三角形全等的判定
SAS
ASA
AAS
SSS
SAS
ASA
AAS
HL
灵活运用各种方法证明直角三角形全等
小结
1.
已知:如图,在△ABC中,AD是∠BAC的角平分线,且BD=CD,DE、DF分别垂直于AB,AC,垂足分别为点E、F.
求证:EB=FC
巩固练习
2.
已知:如图,AB⊥BC,AE⊥ED,
垂足分别为点B、E,AB=AE,∠1=∠2。
求证:BC=DE
巩固练习
3.
已知:如图。AD⊥CD,BC⊥CD,D、C分别为垂足,AB的垂直平分线EF交AB于点E,交CD于点F,BC=DF。
求证:AD=FC
巩固练习
B’
A’
C’
A
B
C
A’
C’
B’
B’
A’
C’
A
C
B
A’
B’
C’
证法三:
证法四:
A’
C’
B’
A
B
C
问题1:在两个直角三角形中,“边、边、角”对应相等的情况有几种?
问题3:你能把我们想要解决的问题用命题的形式来表述吗?
问题探索
对应相等的角:一对直角
对应相等的角的对边:斜边
对应相等的边:对应直角边
问题2:在两个直角三角形中,“边、边、角”对应相等的两个三角形全等吗?这句话可改写为?
19.7直角三角形全等的判定
C’
C
A
B
有两边和其中一边的对角对应相等的两个
三角形全等吗?
B
C’
A
B
A
C
动画演示
对于一般的三角形,“边边角”不可以证明三角形全等
如果两个直角三角形的斜边和一条直角边对应相等,那么这两个直角三角形全等。
已知:如图,在Rt△ABC和Rt△A’B’C’中,∠C=∠C’=
90o
,AB=A’B’
AC=A’C’
求证:
Rt△ABC
≌Rt△A’B’C’
命题
问题探索
A’
C’
B’
A
B
C
B’
A’
C’
B
C
A
问题探索
C
(
)
(
)
已知:如图,在Rt△ABC和Rt△A’B’C’中,∠C=∠C’=
90o
,AB=A’B’
AC=A’C’
求证:
Rt△ABC
≌Rt△A’B’C’
C
A
B
(
)
(
)
1
2
3
4
C’
B’
A’
证法二
问题探索
已知:如图,在Rt△ABC和Rt△A’B’C’中,∠C=∠C’=
90o
,AB=A’B’
AC=A’C’
求证:
Rt△ABC
≌Rt△A’B’C’
如果两个直角三角形的斜边和一条直角边对应相等,那么这两个直角三角形全等。
(简称为H.L.)
定理
命题
探索的结论
B’
A’
C’
B
C
A
(3)AB=A’B’,BC=B’C’
(
)
_____
(2)AC=A’C’,BC=B’C’
(
)
_____
如图,具有下列条件的RT△ABC
和RT△A’B’C’(其中∠C=∠C’=
90o
)是否全等?如果全等在(
)里打“√”,并在“——”上填写判定三角形全等的理由,如果不全等,在(
)里打“×”。
(1)AC=A’C’,∠A=∠A’
(
)
_____
√
√
√
A.S.A.
S.A.S.
H.L.
练一练
B’
A’
C’
B
C
A
(6)
BC=B’C’,∠A=∠A’
(
)
_____
(5)AC=A’C’,AB=A’B’
(
)
_____
练一练
如图,具有下列条件的RT△ABC
和RT△A’B’C’(其中∠C=∠C’=
90o
)是否全等?如果全等在(
)里打“√”,并在“——”上填写判定三角形全等的理由,如果不全等,在(
)里打“×”。
(4)∠A=∠A’,∠B=∠B’
(
)
_____
√
√
A.A.S.
H.L.
×
B’
A’
C’
B
C
A
例1
已知:如图,QD⊥OB,QE⊥OA,垂足分别是点D、E,且QD=QE
求证:点Q在∠AOB的平分线上
例题讲解
逆定理:在一个角的内部(包括顶点)且到角的两边距离相等的点,在这个角的平分线上
已知:如图,在△ABC中,BD⊥AC,CE⊥AB,点D、E为垂足,BD和CE相交于点F,BD=CE.
求证:三角形ABC为等腰三角形
B
A
C
O
E
D
试一试
本节我们学习了哪些什么知识?
有哪些收获、体会,
请
畅所欲言!
畅所欲言!!
畅所欲言!!!
小结
直角三角形全等的判定
一般三角形全等的判定
SAS
ASA
AAS
SSS
SAS
ASA
AAS
HL
灵活运用各种方法证明直角三角形全等
小结
1.
已知:如图,在△ABC中,AD是∠BAC的角平分线,且BD=CD,DE、DF分别垂直于AB,AC,垂足分别为点E、F.
求证:EB=FC
巩固练习
2.
已知:如图,AB⊥BC,AE⊥ED,
垂足分别为点B、E,AB=AE,∠1=∠2。
求证:BC=DE
巩固练习
3.
已知:如图。AD⊥CD,BC⊥CD,D、C分别为垂足,AB的垂直平分线EF交AB于点E,交CD于点F,BC=DF。
求证:AD=FC
巩固练习
B’
A’
C’
A
B
C
A’
C’
B’
B’
A’
C’
A
C
B
A’
B’
C’
证法三:
证法四:
A’
C’
B’
A
B
C
问题1:在两个直角三角形中,“边、边、角”对应相等的情况有几种?
问题3:你能把我们想要解决的问题用命题的形式来表述吗?
问题探索
对应相等的角:一对直角
对应相等的角的对边:斜边
对应相等的边:对应直角边
问题2:在两个直角三角形中,“边、边、角”对应相等的两个三角形全等吗?这句话可改写为?
