沪教版(上海)初中数学八年级第一学期 18.3 反比例函数的图像和性质 课件(共16张ppt)
文档属性
| 名称 | 沪教版(上海)初中数学八年级第一学期 18.3 反比例函数的图像和性质 课件(共16张ppt) |
|
|
| 格式 | zip | ||
| 文件大小 | 350.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-12-25 23:20:19 | ||
图片预览





文档简介
(共16张PPT)
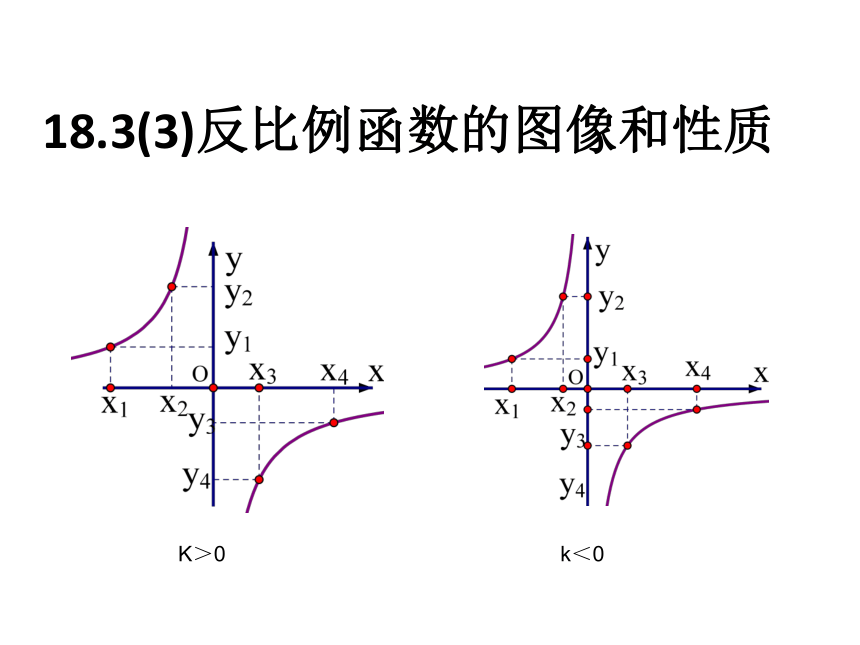
18.3(3)反比例函数的图像和性质
K>0
k<0
1、已知函数
的图像过点(-3,-2),则k=
,图像的两支分别在
象限。
2、函数
的图像过点(
)
,则图像的两支分别在
象限。
6
一、三
二、四
课前练习
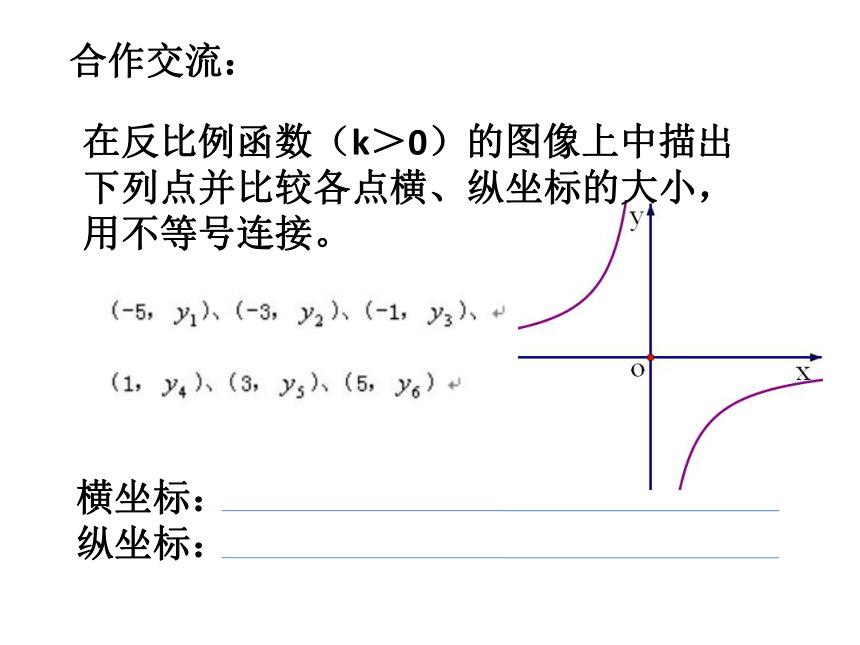
在反比例函数(k>0)的图像上中描出下列点并比较各点横、纵坐标的大小,用不等号连接。
合作交流:
横坐标:
纵坐标:
在反比例函数(k>0)的图像上中描出下列点并比较各点横、纵坐标的大小,用不等号连接。
合作交流:
横坐标:
纵坐标:
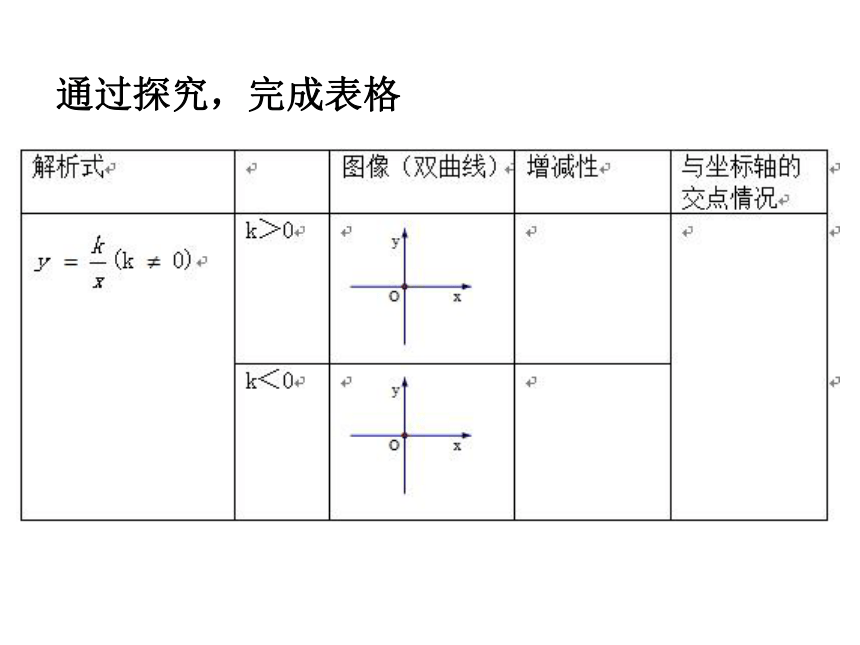
通过探究,完成表格
1、已知反比例函数
(k≠0)的图像过二、四象限,k
0,则在每个象限内,y随x的增大而
。
2、已知反比例函数
(k>0),则其图像过
象限,当x>0时,y随x的减小而
。
3、已知反比例函数
(k≠0),当x<0时,
y随x的增大而增大,则k
0,且图像过
象限。
<
增大
增大
<
二、四
一、三
总结:反比例函数的性质中,已知其中一个都可以判断另外两个。
巩固练习1
巩固练习2
4.
如果点
在反比例函
数
的图象上,如果
的大小关系是(
)
A
5.函数
(
k≠0
)的图像过点(-3,-2),在每个象限内,y的值随x的增大而
。
增大
6.若点
在
的图像上,那么
三个数
的大小关系是
。
例题1:已知反比例函数
(1)如果这个函数的图像过点(2,-1),求k的值;并说出y随x的增大而怎样变化
(2)如果这个函数图像所在的每个象限内y的值随x的增大而减小,求k的取值范围。
巩固练习3
7.已知反比例函数
的图像有一支在第二象限,则k的取值范围是
。
8.已知反比例函数
,当x>0时,y随x的增大而减小,则k的范围是
。
9.已知反比例函数
图像上有
点
如果点
,且当
时,
,
那么k的取值范围是
。
10.如果点
在函数
上,
若
,那么
的大小关系是
。
巩固练习2
1.下列函数中,y随
x的增大而减少的函数是(
)
总结:正反比例的函数性质可以借助于图像,
数形结合,理解记忆。
D
反比例函数必须有条件“在每个象限内”或“x>0”或“x<0”
新课探索二
(1)已知反比例函数
(k≠0)的图像上有一点A(2,3),过点A分别向坐标轴作垂线,那么k=
,两条垂线与两坐标轴围成的长方形的面积是
。
若B(m,6)也在该函数的图像上,过点A分别向坐标轴作垂线,两条垂线与两坐标轴围成的长方形的面积是
。
(2)若A点改为(-5,3)那么k=
,两条垂线与两坐标轴围成的长方形的面积是
。
6
6
6
15
15
若A为反比例函数
(k≠0)的图像上的任意一点,过点A分别向坐标轴作垂线,两条垂线与两坐标轴围成的长方形的面积是
(用k的表达式表示)
总结3
(4)若点A(3,m)在双曲线
的图像上,过A点向x轴作垂线段,交x轴于B点,并联结OA,则
。
2
总结4
过双曲线
(k≠0)的图像上任意点A向x轴
(或y轴)作垂线段,交x轴(或y轴)于C点,
并联结OA,则
(用k来表示)
1、反比例函数三个基本性质是什么?
2、反比例函数图像上独有的性质是什么?
本课小结
18.3(3)反比例函数的图像和性质
K>0
k<0
1、已知函数
的图像过点(-3,-2),则k=
,图像的两支分别在
象限。
2、函数
的图像过点(
)
,则图像的两支分别在
象限。
6
一、三
二、四
课前练习
在反比例函数(k>0)的图像上中描出下列点并比较各点横、纵坐标的大小,用不等号连接。
合作交流:
横坐标:
纵坐标:
在反比例函数(k>0)的图像上中描出下列点并比较各点横、纵坐标的大小,用不等号连接。
合作交流:
横坐标:
纵坐标:
通过探究,完成表格
1、已知反比例函数
(k≠0)的图像过二、四象限,k
0,则在每个象限内,y随x的增大而
。
2、已知反比例函数
(k>0),则其图像过
象限,当x>0时,y随x的减小而
。
3、已知反比例函数
(k≠0),当x<0时,
y随x的增大而增大,则k
0,且图像过
象限。
<
增大
增大
<
二、四
一、三
总结:反比例函数的性质中,已知其中一个都可以判断另外两个。
巩固练习1
巩固练习2
4.
如果点
在反比例函
数
的图象上,如果
的大小关系是(
)
A
5.函数
(
k≠0
)的图像过点(-3,-2),在每个象限内,y的值随x的增大而
。
增大
6.若点
在
的图像上,那么
三个数
的大小关系是
。
例题1:已知反比例函数
(1)如果这个函数的图像过点(2,-1),求k的值;并说出y随x的增大而怎样变化
(2)如果这个函数图像所在的每个象限内y的值随x的增大而减小,求k的取值范围。
巩固练习3
7.已知反比例函数
的图像有一支在第二象限,则k的取值范围是
。
8.已知反比例函数
,当x>0时,y随x的增大而减小,则k的范围是
。
9.已知反比例函数
图像上有
点
如果点
,且当
时,
,
那么k的取值范围是
。
10.如果点
在函数
上,
若
,那么
的大小关系是
。
巩固练习2
1.下列函数中,y随
x的增大而减少的函数是(
)
总结:正反比例的函数性质可以借助于图像,
数形结合,理解记忆。
D
反比例函数必须有条件“在每个象限内”或“x>0”或“x<0”
新课探索二
(1)已知反比例函数
(k≠0)的图像上有一点A(2,3),过点A分别向坐标轴作垂线,那么k=
,两条垂线与两坐标轴围成的长方形的面积是
。
若B(m,6)也在该函数的图像上,过点A分别向坐标轴作垂线,两条垂线与两坐标轴围成的长方形的面积是
。
(2)若A点改为(-5,3)那么k=
,两条垂线与两坐标轴围成的长方形的面积是
。
6
6
6
15
15
若A为反比例函数
(k≠0)的图像上的任意一点,过点A分别向坐标轴作垂线,两条垂线与两坐标轴围成的长方形的面积是
(用k的表达式表示)
总结3
(4)若点A(3,m)在双曲线
的图像上,过A点向x轴作垂线段,交x轴于B点,并联结OA,则
。
2
总结4
过双曲线
(k≠0)的图像上任意点A向x轴
(或y轴)作垂线段,交x轴(或y轴)于C点,
并联结OA,则
(用k来表示)
1、反比例函数三个基本性质是什么?
2、反比例函数图像上独有的性质是什么?
本课小结
