沪教版(上海)初中数学八年级第一学期 18.3 正比例函数与反比例函数 课件(21张)
文档属性
| 名称 | 沪教版(上海)初中数学八年级第一学期 18.3 正比例函数与反比例函数 课件(21张) |

|
|
| 格式 | zip | ||
| 文件大小 | 157.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-12-26 00:00:00 | ||
图片预览








文档简介
(共21张PPT)
正比例函数与反比例函数
函数的概念
2.
自变量的取值范围:
(1)使解析式有意义
(2)实际问题具有实际意义
1.
概念:在一个变化过程中有两个变量x与
y,如果对于x的每一个值,y都有唯一的
值与它对应,那么就说x是自变量,y是x
的函数。
3.列函数关系式与列方程对比;
4.函数的表示方法;
(1)解析法
(2)列表法
(3)图象法
5.函数的图象
(1)画图
(2)识图
三、正比例函数和反比例图象和性质
1.
概念:
形如
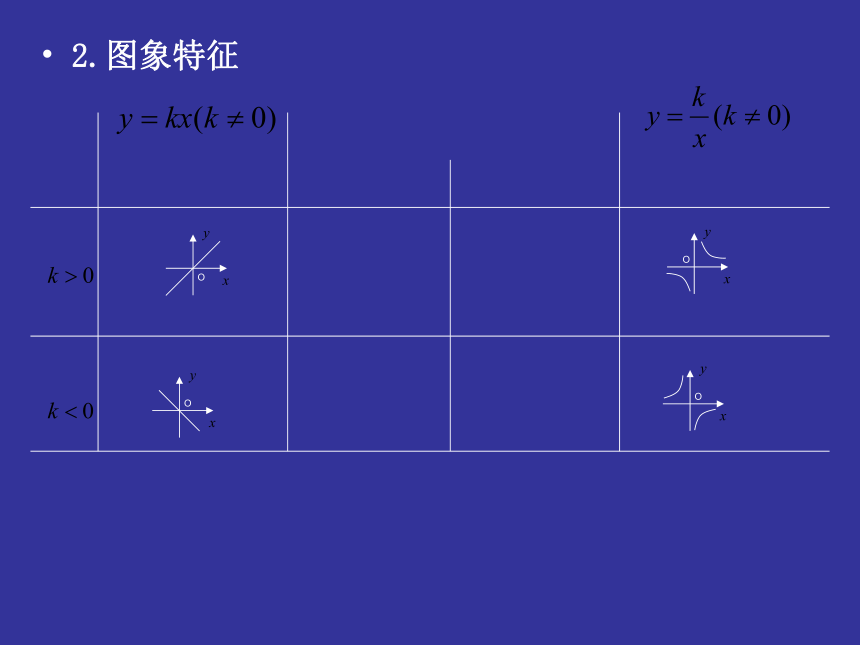
2.图象特征
O
O
O
O
3.性质
当k>0时,y随x的增大而增大
当k<0时,y随x的增大而减小
K>0,图象分布在第一、三象限,
在一、三象限,y随x的增大而减小
K<0,图象分布在第二、四象限,
在二、四象限,y随x的增大而增大
(2) 可用图象上一点的坐标,
或图象上一点引坐标轴的垂线所构成
的矩形的面积结合图象所在象限确定。
4.求解析式
(1)正比例函数,只要知道图象上除原点
外的任一点坐标;
1.在直角坐标系中,O为坐标原点,已知A
(1,1),在x轴上确定点P,使△AOP为
等腰三角形,则符合条件的点P的个数共
有(
)
A.
1个
B.
2个
C.
3个
D.
4个
D
2.某气球内充满了一定质量的气体,当温度不变时,气体内气压P(kpa)是气体体积V(m3)的反比例函数,其图象如图所示,当气球内的气压大于140kpa时,气球将爆炸,为了安全起见,气体体积应( )
A.不大于
m3
B.不小于
m3
C.不大于
m3
D.不小于
m3
A(0.8,120)
B
3.某校八年级学生到距学校6千米的郊外春游,一部分同学步行,另一部分同学骑自行车,沿相同路线前往,如图,分别表示步行和骑车的同学前往目的地所走路程y(千米)与所用时间x(分钟)之间的函数图象,则
下列判断错误的是( )
D
A.骑车同学比步行的同学晚出发30分钟
B.步行速度为6千米/时
C.骑车的同学从出发到追上步行的同学用
了20分钟
D.骑车的同学和步行的同学同时到达目的地
4.某闭合电路中,电源电压为定值,电流
I(A)与电阻R( )成反比例,图中表
示的是该电路中电流I与电阻R之间函数 关系的图象,则用电阻R表示电流I的函
数解析式为( )
A. B.
C.
D.
B(1,3)
I
R
C
5.函数 与函数 的图象在同
一平面直角坐标系内的交点个数(
)
A.
1个
B.
2个
C.
3个
D.
0个
B
6.函数 中自变量x的取值范围是
( )
A.x≥2
B.
x≥2且x≠-3
C.
x>2
D.
x≠-3
A
7.反比例函数 与正比例函数
在同一坐标系中的图象不可
能是( )
A
B
C
D
x
y
x
y
x
y
x
y
D
8.正比例函数y=x与反比例函数
的
图象相交于A、C两点,AB⊥x轴于B,
CD
⊥x轴于D(如图),则四边形ABCD
的面积为( )
A.1
B.
C.2
D.
C
9.若双曲线 经过点A(m,-2m),则m的值为___________
10.任意写出一个图象经过二、四象限的反
比例函数的解析式____________
11.一化工厂生产某种产品出厂价为500元/吨,其原材料成本(含设备损
耗)为200元/吨,同时,生产1吨该产品需付环保处理费及各项支出共计100元,写出利润y(元)与产品销量x(吨)之间的函数关系式为_______,销售该产品______吨,才能获得10万元利润。
y=200x
500
12.如图,△P1OA1、△P2A1A2是等腰直角三角形,点P1、P2在函数 的图
象上,斜边
OA1,A1A2都在x轴上,则点A2的坐标是(
,
)
0
A1
y
x
O
A2
P2
P1
13.在一次蜡烛燃烧实验中,甲、乙两根蜡
烛燃烧时剩余部分的高度y(cm)与燃
烧时间x(h)的关系如图所示,请根据
图象所提供的信息解答下列问题。
甲
乙
甲、乙两根蜡烛燃烧前的高度分别是____________;
从点燃到燃尽所用的时间分别是____________;
30cm
,25cm
2h
,2.5h
14.夏天容易发生腹泻等肠道疾病,某市医药公司的甲、乙两仓库内分别存有医治腹泻的药品80箱和70箱,现需要将库存的药品调往南县100箱和沅江50箱,已知从甲、乙两仓库运送药品到两地的费用(元/箱)如下表所示:
(1)从甲仓库运送到南县的药品为x箱,求总费用y(元)与x(箱)之间的函数关系式,并写出x的取值范围。
(2)求出最低费用,并说明总费用最低时的调配方案。
∴y=14x+10(80-x)+20(100-x)+8(x-30)
=-8x+2560
x的取值范围为:30≤
x≤80
(2)
∵y=-8x+2560中,y随x的增大而减小,
又∵30≤
x≤80
∴x=80时,y最小=1920(元)
总费用最低时的调配方案为:甲仓库80箱全部运往南县,乙仓库20箱运送南县,50箱运送沅江。
解(1)设从甲仓库运送到南县的药品为x
箱,则从甲仓库运送到沅江的药品为(80-x)箱,从乙仓库运送到南县的药品为(100-x)箱,从乙仓库运送到沅江的药品为(x-30)箱。
正比例函数与反比例函数
函数的概念
2.
自变量的取值范围:
(1)使解析式有意义
(2)实际问题具有实际意义
1.
概念:在一个变化过程中有两个变量x与
y,如果对于x的每一个值,y都有唯一的
值与它对应,那么就说x是自变量,y是x
的函数。
3.列函数关系式与列方程对比;
4.函数的表示方法;
(1)解析法
(2)列表法
(3)图象法
5.函数的图象
(1)画图
(2)识图
三、正比例函数和反比例图象和性质
1.
概念:
形如
2.图象特征
O
O
O
O
3.性质
当k>0时,y随x的增大而增大
当k<0时,y随x的增大而减小
K>0,图象分布在第一、三象限,
在一、三象限,y随x的增大而减小
K<0,图象分布在第二、四象限,
在二、四象限,y随x的增大而增大
(2) 可用图象上一点的坐标,
或图象上一点引坐标轴的垂线所构成
的矩形的面积结合图象所在象限确定。
4.求解析式
(1)正比例函数,只要知道图象上除原点
外的任一点坐标;
1.在直角坐标系中,O为坐标原点,已知A
(1,1),在x轴上确定点P,使△AOP为
等腰三角形,则符合条件的点P的个数共
有(
)
A.
1个
B.
2个
C.
3个
D.
4个
D
2.某气球内充满了一定质量的气体,当温度不变时,气体内气压P(kpa)是气体体积V(m3)的反比例函数,其图象如图所示,当气球内的气压大于140kpa时,气球将爆炸,为了安全起见,气体体积应( )
A.不大于
m3
B.不小于
m3
C.不大于
m3
D.不小于
m3
A(0.8,120)
B
3.某校八年级学生到距学校6千米的郊外春游,一部分同学步行,另一部分同学骑自行车,沿相同路线前往,如图,分别表示步行和骑车的同学前往目的地所走路程y(千米)与所用时间x(分钟)之间的函数图象,则
下列判断错误的是( )
D
A.骑车同学比步行的同学晚出发30分钟
B.步行速度为6千米/时
C.骑车的同学从出发到追上步行的同学用
了20分钟
D.骑车的同学和步行的同学同时到达目的地
4.某闭合电路中,电源电压为定值,电流
I(A)与电阻R( )成反比例,图中表
示的是该电路中电流I与电阻R之间函数 关系的图象,则用电阻R表示电流I的函
数解析式为( )
A. B.
C.
D.
B(1,3)
I
R
C
5.函数 与函数 的图象在同
一平面直角坐标系内的交点个数(
)
A.
1个
B.
2个
C.
3个
D.
0个
B
6.函数 中自变量x的取值范围是
( )
A.x≥2
B.
x≥2且x≠-3
C.
x>2
D.
x≠-3
A
7.反比例函数 与正比例函数
在同一坐标系中的图象不可
能是( )
A
B
C
D
x
y
x
y
x
y
x
y
D
8.正比例函数y=x与反比例函数
的
图象相交于A、C两点,AB⊥x轴于B,
CD
⊥x轴于D(如图),则四边形ABCD
的面积为( )
A.1
B.
C.2
D.
C
9.若双曲线 经过点A(m,-2m),则m的值为___________
10.任意写出一个图象经过二、四象限的反
比例函数的解析式____________
11.一化工厂生产某种产品出厂价为500元/吨,其原材料成本(含设备损
耗)为200元/吨,同时,生产1吨该产品需付环保处理费及各项支出共计100元,写出利润y(元)与产品销量x(吨)之间的函数关系式为_______,销售该产品______吨,才能获得10万元利润。
y=200x
500
12.如图,△P1OA1、△P2A1A2是等腰直角三角形,点P1、P2在函数 的图
象上,斜边
OA1,A1A2都在x轴上,则点A2的坐标是(
,
)
0
A1
y
x
O
A2
P2
P1
13.在一次蜡烛燃烧实验中,甲、乙两根蜡
烛燃烧时剩余部分的高度y(cm)与燃
烧时间x(h)的关系如图所示,请根据
图象所提供的信息解答下列问题。
甲
乙
甲、乙两根蜡烛燃烧前的高度分别是____________;
从点燃到燃尽所用的时间分别是____________;
30cm
,25cm
2h
,2.5h
14.夏天容易发生腹泻等肠道疾病,某市医药公司的甲、乙两仓库内分别存有医治腹泻的药品80箱和70箱,现需要将库存的药品调往南县100箱和沅江50箱,已知从甲、乙两仓库运送药品到两地的费用(元/箱)如下表所示:
(1)从甲仓库运送到南县的药品为x箱,求总费用y(元)与x(箱)之间的函数关系式,并写出x的取值范围。
(2)求出最低费用,并说明总费用最低时的调配方案。
∴y=14x+10(80-x)+20(100-x)+8(x-30)
=-8x+2560
x的取值范围为:30≤
x≤80
(2)
∵y=-8x+2560中,y随x的增大而减小,
又∵30≤
x≤80
∴x=80时,y最小=1920(元)
总费用最低时的调配方案为:甲仓库80箱全部运往南县,乙仓库20箱运送南县,50箱运送沅江。
解(1)设从甲仓库运送到南县的药品为x
箱,则从甲仓库运送到沅江的药品为(80-x)箱,从乙仓库运送到南县的药品为(100-x)箱,从乙仓库运送到沅江的药品为(x-30)箱。
