沪教版(上海)初中数学八年级第一学期 17.1 一元二次方程的概念 课件(共16张ppt)
文档属性
| 名称 | 沪教版(上海)初中数学八年级第一学期 17.1 一元二次方程的概念 课件(共16张ppt) |

|
|
| 格式 | zip | ||
| 文件大小 | 288.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-12-25 00:00:00 | ||
图片预览


文档简介
(共16张PPT)
§17.1一元二次方程的概念
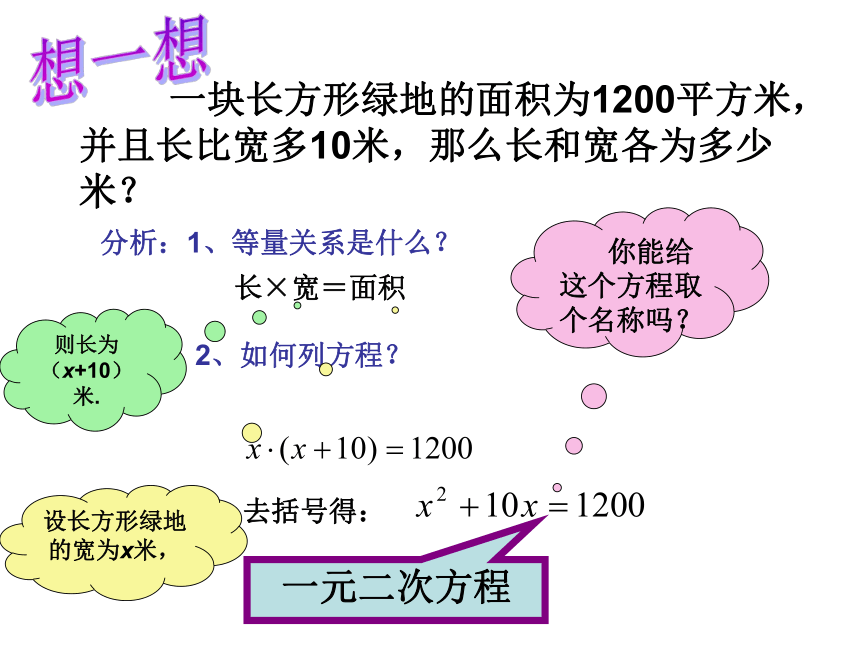
一块长方形绿地的面积为1200平方米,并且长比宽多10米,那么长和宽各为多少米?
想一想
分析:1、等量关系是什么?
长×宽=面积
2、如何列方程?
去括号得:
你能给这个方程取个名称吗?
设长方形绿地的宽为x米,
一元二次方程
则长为(x+10)米.
只含有一个未知数且未知数的最高次数是2的整式方程叫做一元二次方程.
试一试:下列方程哪些是一元二次方程?
不是整式方程.
去括号得:8x+7=0,是一元一次方程
.
它是不是一元二次方程呢?
学一学
√
√
√
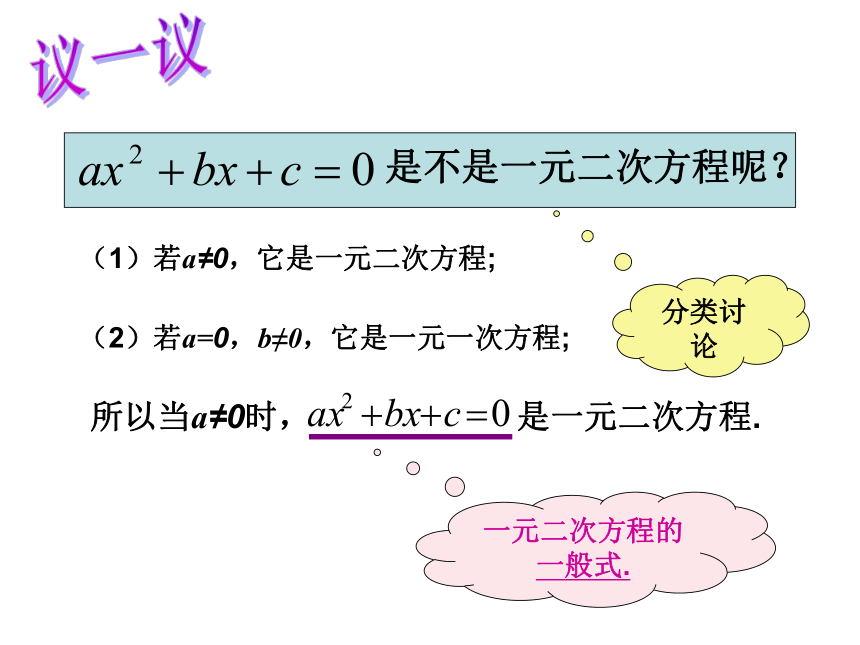
是不是一元二次方程呢?
(1)若a≠0,它是一元二次方程;
(2)若a=0,b≠0,它是一元一次方程;
所以当a≠0时,
是一元二次方程.
议一议
一元二次方程的一般式.
分类讨论
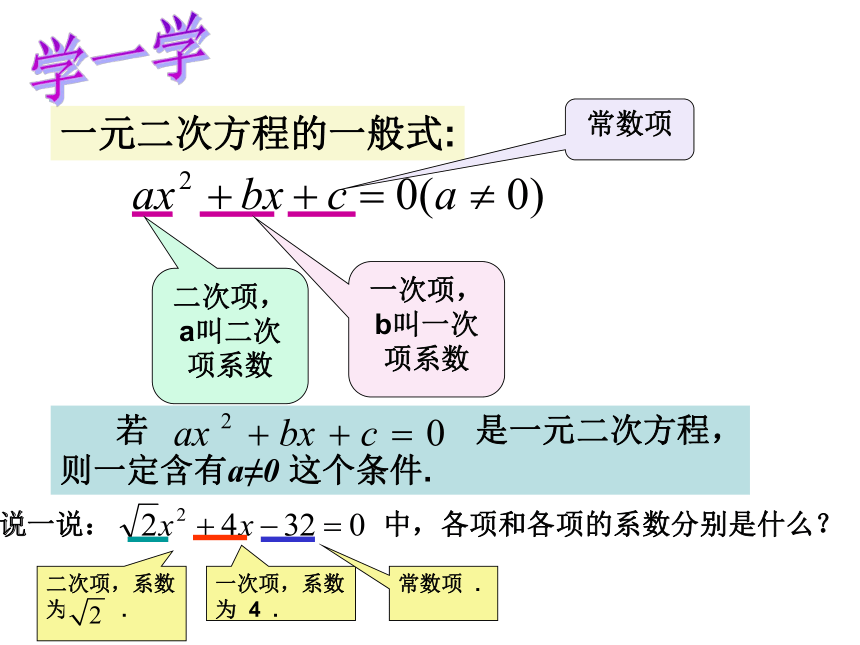
一元二次方程的一般式:
常数项
若
是一元二次方程,
则一定含有a≠0
这个条件.
二次项,a叫二次项系数
一次项,b叫一次项系数
说一说:
中,各项和各项的系数分别是什么?
学一学
二次项,系数为
.
一次项,系数为
4
.
常数项
.
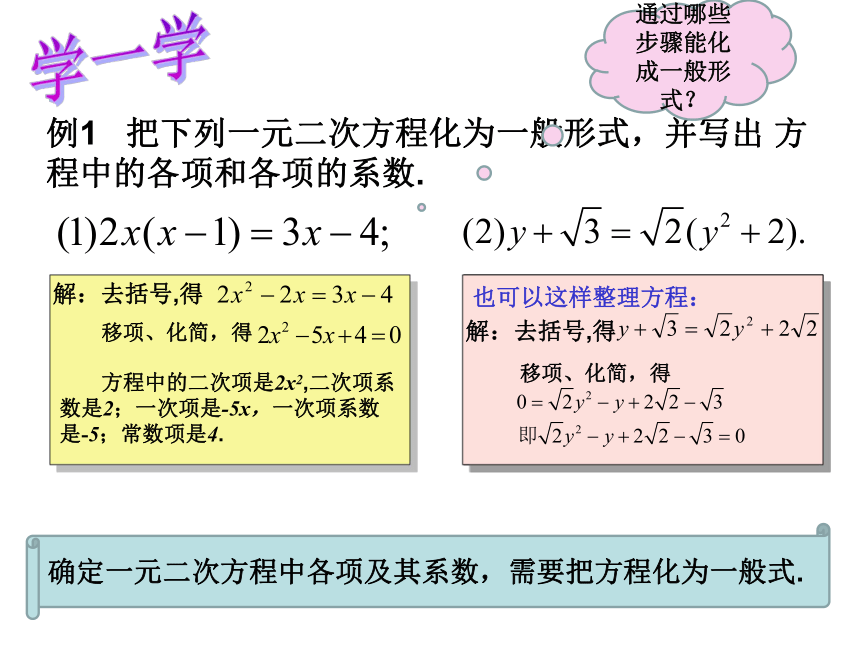
例1
把下列一元二次方程化为一般形式,并写出
方程中的各项和各项的系数.
通过哪些步骤能化成一般形式?
确定一元二次方程中各项及其系数,需要把方程化为一般式.
学一学
解:去括号,得
移项、化简,得
方程中的二次项是2x2,二次项系
数是2;一次项是-5x,一次项系数
是-5;常数项是4.
解:去括号,得
移项、化简,得
方程中的二次项是
,二次项系
数是
;一次项是y
,一次项系数
是1;常数项是
.
解:去括号,得
移项、化简,得
也可以这样整理方程:
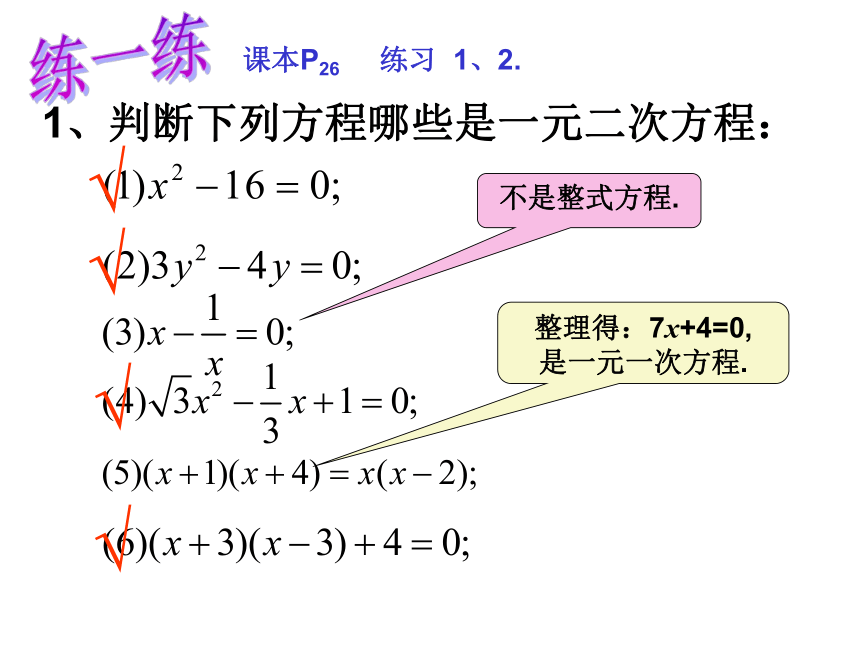
1、判断下列方程哪些是一元二次方程:
练一练
√
√
不是整式方程.
√
整理得:7x+4=0,
是一元一次方程.
√
课本P26
练习
1、2.
2、将下列一元二次方程化为一般式,并分别指出它们的二次项系数、一次项系数和常数项:
练一练
2、将下列一元二次方程化为一般式,并分别指出它们的二次项系数、一次项系数和常数项:
练一练
例2
判断2,5,-4是不是一元二次方程
的根?
分析:1、什么是方程的根?
2、什么是方程的解?
只含有一个未知数的方程的解也叫做方程的根.
学一学
能够使方程两边相等的未知数的值叫做方程的解.
例2
判断2,5,-4是不是一元二次方程
的根?
解:化成一般式得:
把x=2分别代入方程
的左边和右边得:
左边=
右边=
0;
∵左边=右边,
∴x=2是这个一元二次方程的根.
左边=
右边=
0;
∵左边≠右边,
∴x=5不是这个一元二次方程的根.
把x=5分别代入方程
的左边和右边得:
左边=
右边=
0;
∵左边=右边,
∴x=-4是这个一元二次方程的根.
把x=-4分别代入方程的左边和右边得:
学一学
从这个例题看出一元二次方程的根不止一个,与一元一次方程只有一个根是不同的.
例3
关于
x
的方程
(1)在什么条件下是一元二次方程?
(2)在什么条件下是一元一次方程?
分析:1、要判断一个方程是否是一元二次
方程,应先做什么?
应先把方程整理成一般式.
2、整理结果是什么?
3、满足什么条件才能是一元二次方程?
4、满足什么条件才能是一元一次方程?
想一想
二次项系数不等于0,
即
二次项系数为0,且一次项系数不为0,
即
例3
关于
x
的方程
想一想
解:方程化为一般式为
(1)当
,即
时,方程是一元二次方程;
(2)当
即
时,方程是一元二次方程.
1、当m为何值时,关于x的方程
是一元二次方程?
练一练
2、已知关于x的一元二次方程
有一个根是0,求m的值.
解:整理得
当m-1≠0,即m≠1时,此方程是一元二次方程.
解:把x
=
0代入原方程得
0
+
0+m-
4
=
0,
解得
m=4,
所以当m的值为4时,原方程有一个根是0.
课本P26
练习
3、4.
这节课你有什么收获和体会?
谈一谈
1.一元二次方程的概念.
小结
在一元二次方程概念的形成过程中,体会了类比的数学思想.
只含有一个未知数且未知数的最高次数是2的整式方程叫做一元二次方程.
2.一元二次方程的一般式、各项及其系数.
常数项.
一次项,b叫一次项系数.
二次项,a叫二次项系数.
3.判断一个数是不是一元二次方程的根.
§17.1一元二次方程的概念
一块长方形绿地的面积为1200平方米,并且长比宽多10米,那么长和宽各为多少米?
想一想
分析:1、等量关系是什么?
长×宽=面积
2、如何列方程?
去括号得:
你能给这个方程取个名称吗?
设长方形绿地的宽为x米,
一元二次方程
则长为(x+10)米.
只含有一个未知数且未知数的最高次数是2的整式方程叫做一元二次方程.
试一试:下列方程哪些是一元二次方程?
不是整式方程.
去括号得:8x+7=0,是一元一次方程
.
它是不是一元二次方程呢?
学一学
√
√
√
是不是一元二次方程呢?
(1)若a≠0,它是一元二次方程;
(2)若a=0,b≠0,它是一元一次方程;
所以当a≠0时,
是一元二次方程.
议一议
一元二次方程的一般式.
分类讨论
一元二次方程的一般式:
常数项
若
是一元二次方程,
则一定含有a≠0
这个条件.
二次项,a叫二次项系数
一次项,b叫一次项系数
说一说:
中,各项和各项的系数分别是什么?
学一学
二次项,系数为
.
一次项,系数为
4
.
常数项
.
例1
把下列一元二次方程化为一般形式,并写出
方程中的各项和各项的系数.
通过哪些步骤能化成一般形式?
确定一元二次方程中各项及其系数,需要把方程化为一般式.
学一学
解:去括号,得
移项、化简,得
方程中的二次项是2x2,二次项系
数是2;一次项是-5x,一次项系数
是-5;常数项是4.
解:去括号,得
移项、化简,得
方程中的二次项是
,二次项系
数是
;一次项是y
,一次项系数
是1;常数项是
.
解:去括号,得
移项、化简,得
也可以这样整理方程:
1、判断下列方程哪些是一元二次方程:
练一练
√
√
不是整式方程.
√
整理得:7x+4=0,
是一元一次方程.
√
课本P26
练习
1、2.
2、将下列一元二次方程化为一般式,并分别指出它们的二次项系数、一次项系数和常数项:
练一练
2、将下列一元二次方程化为一般式,并分别指出它们的二次项系数、一次项系数和常数项:
练一练
例2
判断2,5,-4是不是一元二次方程
的根?
分析:1、什么是方程的根?
2、什么是方程的解?
只含有一个未知数的方程的解也叫做方程的根.
学一学
能够使方程两边相等的未知数的值叫做方程的解.
例2
判断2,5,-4是不是一元二次方程
的根?
解:化成一般式得:
把x=2分别代入方程
的左边和右边得:
左边=
右边=
0;
∵左边=右边,
∴x=2是这个一元二次方程的根.
左边=
右边=
0;
∵左边≠右边,
∴x=5不是这个一元二次方程的根.
把x=5分别代入方程
的左边和右边得:
左边=
右边=
0;
∵左边=右边,
∴x=-4是这个一元二次方程的根.
把x=-4分别代入方程的左边和右边得:
学一学
从这个例题看出一元二次方程的根不止一个,与一元一次方程只有一个根是不同的.
例3
关于
x
的方程
(1)在什么条件下是一元二次方程?
(2)在什么条件下是一元一次方程?
分析:1、要判断一个方程是否是一元二次
方程,应先做什么?
应先把方程整理成一般式.
2、整理结果是什么?
3、满足什么条件才能是一元二次方程?
4、满足什么条件才能是一元一次方程?
想一想
二次项系数不等于0,
即
二次项系数为0,且一次项系数不为0,
即
例3
关于
x
的方程
想一想
解:方程化为一般式为
(1)当
,即
时,方程是一元二次方程;
(2)当
即
时,方程是一元二次方程.
1、当m为何值时,关于x的方程
是一元二次方程?
练一练
2、已知关于x的一元二次方程
有一个根是0,求m的值.
解:整理得
当m-1≠0,即m≠1时,此方程是一元二次方程.
解:把x
=
0代入原方程得
0
+
0+m-
4
=
0,
解得
m=4,
所以当m的值为4时,原方程有一个根是0.
课本P26
练习
3、4.
这节课你有什么收获和体会?
谈一谈
1.一元二次方程的概念.
小结
在一元二次方程概念的形成过程中,体会了类比的数学思想.
只含有一个未知数且未知数的最高次数是2的整式方程叫做一元二次方程.
2.一元二次方程的一般式、各项及其系数.
常数项.
一次项,b叫一次项系数.
二次项,a叫二次项系数.
3.判断一个数是不是一元二次方程的根.
