6.7用相似三角形解决问题(1)-苏科版九年级数学下册培优训练(Word版 含答案)
文档属性
| 名称 | 6.7用相似三角形解决问题(1)-苏科版九年级数学下册培优训练(Word版 含答案) |

|
|
| 格式 | doc | ||
| 文件大小 | 578.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-12-26 00:00:00 | ||
图片预览


文档简介
6.7用相似三角形解决问题(1)-苏科版九年级数学下册 培优训练
一、选择题
1、在下面的图形中,表示两棵小树在同一时刻阳光下的影子的是 ( )
2、为了加强视力保护意识,小明要在书房里挂一张视力表.由于书房空间狭小,他想根据测试距离为5 m的大视力表制作一个测试距离为3 m的小视力表.如图,如果大视力表中“E”的高度是3.5 cm,那么小视力表中相应“E”的高度是( )
A.3 cm B.2.5 cm C.2.3 cm D.2.1 cm
3、如图是小明测量某古城墙高度的示意图,点P处放一水平的平面镜,然后,后退至点B,从点A经平面镜刚好看到古城墙CD的顶端C处,已知AB⊥BD,CD⊥BD,且测得AB=1.2米,BP=1.8米,PD=12米,那么该古城墙的高度是 ( )
A.6米 B.8米 C.18米 D.24米
4、如图,小明在打网球时,要使球恰好能打过网,而且落在离网5米的位置上,
则球拍击球的高度h应为( )
A.2.7 m B.1.8 m C.0.9 m D.6 m
5、如图,A,B两地被池塘隔开,小明通过下列方法测出了A、B间的距离:先在AB外选一点C,然后测出AC,BC的中点M,N,并测量出MN的长为12m,由此他就知道了A、B间的距离.有关他这次探究活动的描述错误的是( )
A.AB=24m B. MN∥AB C. △CMN∽△CAB D. CM:MA=1:2
6、如图,利用标杆BE测量建筑物的高度.已知标杆BE高1.2 m,测得AB=1.6 m,BC=12.4 m,则建筑物CD的高是( )
A.9.3 m B.10.5 m C.12.4 m D.14 m
7、在同一时刻两根木竿在太阳光下的影子如图所示,其中木竿AB=2 m,它的影子BC=1.6 m,木竿PQ的影子有一部分落在了墙上,PM=1.2 m,MN=0.8 m,则木竿PQ的长度为( )
A.2.3 m B.2.5 m C.2.4 m D.2.1 m
二、填空题
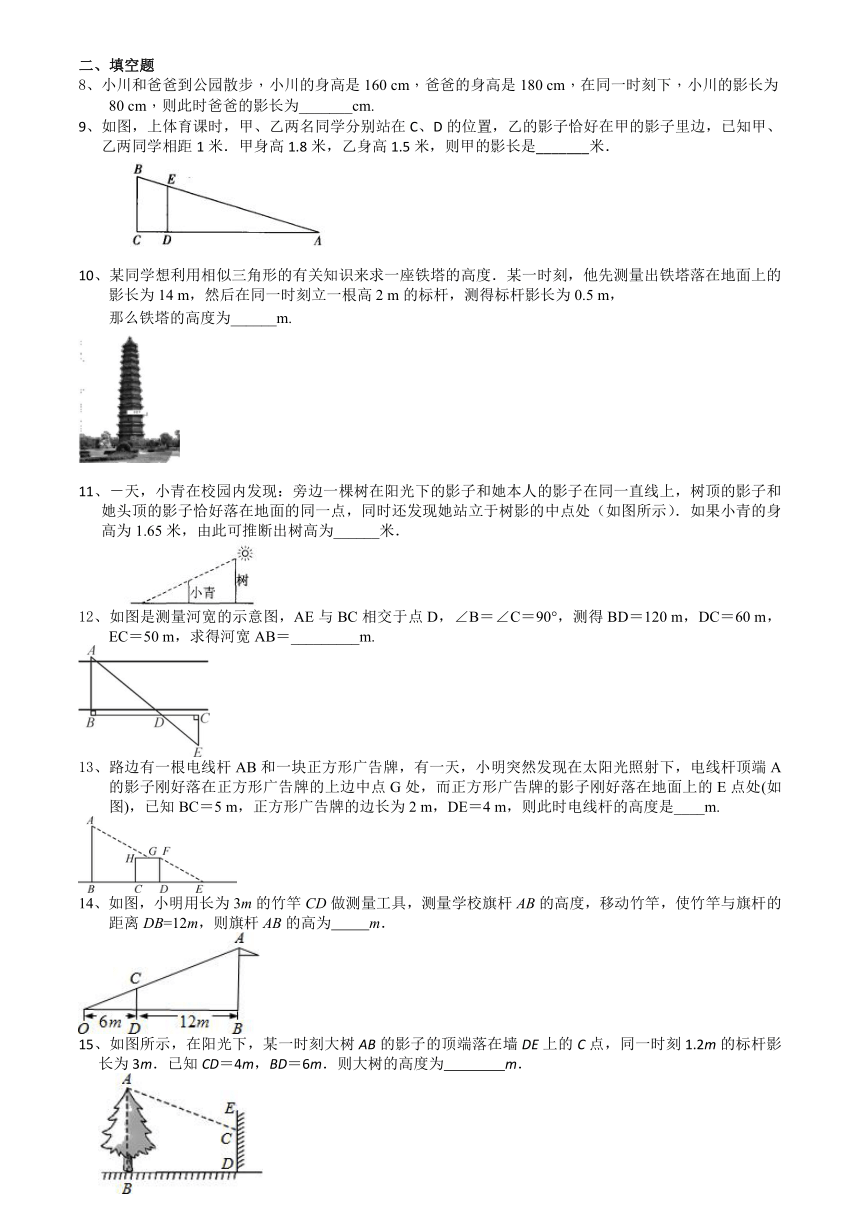
8、小川和爸爸到公园散步,小川的身高是160 cm,爸爸的身高是180 cm,在同一时刻下,小川的影长为80 cm,则此时爸爸的影长为_______cm.
9、如图,上体育课时,甲、乙两名同学分别站在C、D的位置,乙的影子恰好在甲的影子里边,已知甲、乙两同学相距1米.甲身高1.8米,乙身高1.5米,则甲的影长是_______米.
10、某同学想利用相似三角形的有关知识来求一座铁塔的高度.某一时刻,他先测量出铁塔落在地面上的影长为14 m,然后在同一时刻立一根高2 m的标杆,测得标杆影长为0.5 m,
那么铁塔的高度为______m.
11、-天,小青在校园内发现:旁边一棵树在阳光下的影子和她本人的影子在同一直线上,树顶的影子和她头顶的影子恰好落在地面的同一点,同时还发现她站立于树影的中点处(如图所示).如果小青的身高为1.65米,由此可推断出树高为______米.
12、如图是测量河宽的示意图,AE与BC相交于点D,∠B=∠C=90°,测得BD=120 m,DC=60 m,EC=50 m,求得河宽AB=_________m.
13、路边有一根电线杆AB和一块正方形广告牌,有一天,小明突然发现在太阳光照射下,电线杆顶端A的影子刚好落在正方形广告牌的上边中点G处,而正方形广告牌的影子刚好落在地面上的E点处(如图),已知BC=5 m,正方形广告牌的边长为2 m,DE=4 m,则此时电线杆的高度是____m.
14、如图,小明用长为3m的竹竿CD做测量工具,测量学校旗杆AB的高度,移动竹竿,使竹竿与旗杆的距离DB=12m,则旗杆AB的高为 m.
15、如图所示,在阳光下,某一时刻大树AB的影子的顶端落在墙DE上的C点,同一时刻1.2m的标杆影长为3m.已知CD=4m,BD=6m.则大树的高度为 m.
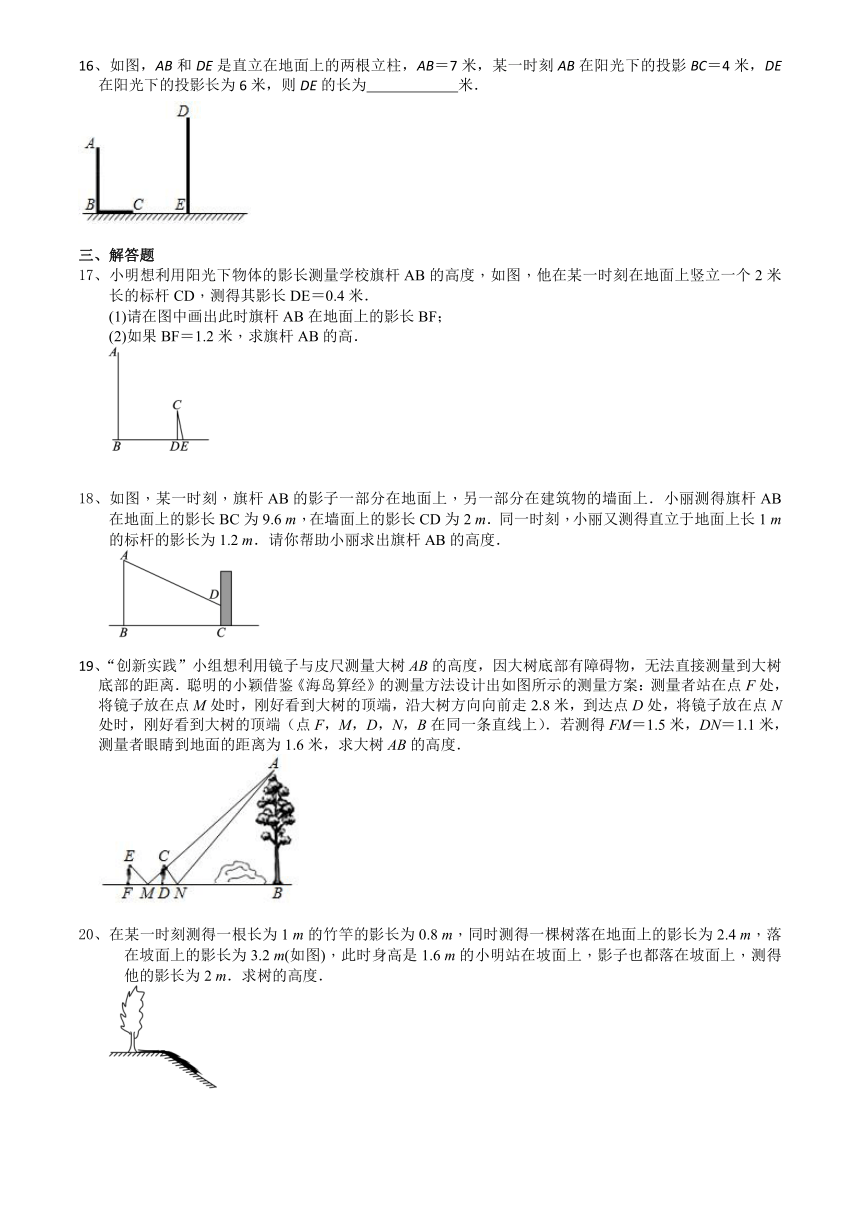
16、如图,AB和DE是直立在地面上的两根立柱,AB=7米,某一时刻AB在阳光下的投影BC=4米,DE在阳光下的投影长为6米,则DE的长为 米.
三、解答题
17、小明想利用阳光下物体的影长测量学校旗杆AB的高度,如图,他在某一时刻在地面上竖立一个2米长的标杆CD,测得其影长DE=0.4米.
(1)请在图中画出此时旗杆AB在地面上的影长BF;
(2)如果BF=1.2米,求旗杆AB的高.
18、如图,某一时刻,旗杆AB的影子一部分在地面上,另一部分在建筑物的墙面上.小丽测得旗杆AB在地面上的影长BC为9.6 m,在墙面上的影长CD为2 m.同一时刻,小丽又测得直立于地面上长1 m的标杆的影长为1.2 m.请你帮助小丽求出旗杆AB的高度.
19、“创新实践”小组想利用镜子与皮尺测量大树AB的高度,因大树底部有障碍物,无法直接测量到大树底部的距离.聪明的小颖借鉴《海岛算经》的测量方法设计出如图所示的测量方案:测量者站在点F处,将镜子放在点M处时,刚好看到大树的顶端,沿大树方向向前走2.8米,到达点D处,将镜子放在点N处时,刚好看到大树的顶端(点F,M,D,N,B在同一条直线上).若测得FM=1.5米,DN=1.1米,测量者眼睛到地面的距离为1.6米,求大树AB的高度.
20、在某一时刻测得一根长为1 m的竹竿的影长为0.8 m,同时测得一棵树落在地面上的影长为2.4 m,落在坡面上的影长为3.2 m(如图),此时身高是1.6 m的小明站在坡面上,影子也都落在坡面上,测得他的影长为2 m.求树的高度.
6.7用相似三角形解决问题(1)-苏科版九年级数学下册 培优训练(答案)
一、选择题
1、在下面的图形中,表示两棵小树在同一时刻阳光下的影子的是 ( D )
2、为了加强视力保护意识,小明要在书房里挂一张视力表.由于书房空间狭小,他想根据测试距离为5 m的大视力表制作一个测试距离为3 m的小视力表.如图,如果大视力表中“E”的高度是3.5 cm,那么小视力表中相应“E”的高度是( )
A.3 cm B.2.5 cm C.2.3 cm D.2.1 cm
[解析] 如图,由题意得CD∥AB,∴=.
∵AB=3.5 cm,BE=5 m,DE=3 m,∴=, ∴CD=2.1 cm.故选D.
3、如图是小明测量某古城墙高度的示意图,点P处放一水平的平面镜,然后,后退至点B,从点A经平面镜刚好看到古城墙CD的顶端C处,已知AB⊥BD,CD⊥BD,且测得AB=1.2米,BP=1.8米,PD=12米,那么该古城墙的高度是 ( B )
A.6米 B.8米 C.18米 D.24米
4、如图,小明在打网球时,要使球恰好能打过网,而且落在离网5米的位置上,
则球拍击球的高度h应为( A )
A.2.7 m B.1.8 m C.0.9 m D.6 m
5、如图,A,B两地被池塘隔开,小明通过下列方法测出了A、B间的距离:先在AB外选一点C,然后测出AC,BC的中点M,N,并测量出MN的长为12m,由此他就知道了A、B间的距离.有关他这次探究活动的描述错误的是( D )
A.AB=24m B. MN∥AB C. △CMN∽△CAB D. CM:MA=1:2
6、如图,利用标杆BE测量建筑物的高度.已知标杆BE高1.2 m,测得AB=1.6 m,BC=12.4 m,则建筑物CD的高是( B )
A.9.3 m B.10.5 m C.12.4 m D.14 m
7、在同一时刻两根木竿在太阳光下的影子如图所示,其中木竿AB=2 m,它的影子BC=1.6 m,木竿PQ的影子有一部分落在了墙上,PM=1.2 m,MN=0.8 m,则木竿PQ的长度为( A )
A.2.3 m B.2.5 m C.2.4 m D.2.1 m
二、填空题
8、小川和爸爸到公园散步,小川的身高是160 cm,爸爸的身高是180 cm,在同一时刻下,小川的影长为80 cm,则此时爸爸的影长为__90______cm.
9、如图,上体育课时,甲、乙两名同学分别站在C、D的位置,乙的影子恰好在甲的影子里边,已知甲、乙两同学相距1米.甲身高1.8米,乙身高1.5米,则甲的影长是__6 _____米.
10、某同学想利用相似三角形的有关知识来求一座铁塔的高度.某一时刻,他先测量出铁塔落在地面上的影长为14 m,然后在同一时刻立一根高2 m的标杆,测得标杆影长为0.5 m,
那么铁塔的高度为____56___m.
11、-天,小青在校园内发现:旁边一棵树在阳光下的影子和她本人的影子在同一直线上,树顶的影子和她头顶的影子恰好落在地面的同一点,同时还发现她站立于树影的中点处(如图所示).如果小青的身高为1.65米,由此可推断出树高为__3.3 _____米.
12、如图是测量河宽的示意图,AE与BC相交于点D,∠B=∠C=90°,测得BD=120 m,DC=60 m,EC=50 m,求得河宽AB=__100 ________m.
13、路边有一根电线杆AB和一块正方形广告牌,有一天,小明突然发现在太阳光照射下,电线杆顶端A的影子刚好落在正方形广告牌的上边中点G处,而正方形广告牌的影子刚好落在地面上的E点处(如图),已知BC=5 m,正方形广告牌的边长为2 m,DE=4 m,则此时电线杆的高度是___5__m.
14、如图,小明用长为3m的竹竿CD做测量工具,测量学校旗杆AB的高度,移动竹竿,使竹竿与旗杆的距离DB=12m,则旗杆AB的高为 9 m.
15、如图所示,在阳光下,某一时刻大树AB的影子的顶端落在墙DE上的C点,同一时刻1.2m的标杆影长为3m.已知CD=4m,BD=6m.则大树的高度为 m.
【解答】解:作CF⊥AB于F,如图,
易得四边形BDCF为矩形,
∴CF=BD=6,BF=CD=4,
∵同一时刻1.2m的标杆影长为3m,
∴=,即=,解得AF=3.2,
∴AB=AF+BF=3.2+4=7.2(m).
故答案为7.2.
16、如图,AB和DE是直立在地面上的两根立柱,AB=7米,某一时刻AB在阳光下的投影BC=4米,DE在阳光下的投影长为6米,则DE的长为 米.
【解答】解:如图所示,
连接AC,过点D作DF∥AC交地面于点F,
∵同一时刻物高与物高的比等于影长与影长的比,∴=,即=
∴DE=.则DE的长为米. 故答案为.
三、解答题
17、小明想利用阳光下物体的影长测量学校旗杆AB的高度,如图,他在某一时刻在地面上竖立一个2米长的标杆CD,测得其影长DE=0.4米.
(1)请在图中画出此时旗杆AB在地面上的影长BF;
(2)如果BF=1.2米,求旗杆AB的高.
解:(1)如图所示.
(2)∵AF∥CE,∴∠AFB=∠CED.
又∵∠ABF=∠CDE=90°,∴△ABF∽△CDE,∴=,解得AB=6米.
答:旗杆AB的高为6米.
18、如图,某一时刻,旗杆AB的影子一部分在地面上,另一部分在建筑物的墙面上.小丽测得旗杆AB在地面上的影长BC为9.6 m,在墙面上的影长CD为2 m.同一时刻,小丽又测得直立于地面上长1 m的标杆的影长为1.2 m.请你帮助小丽求出旗杆AB的高度.
解:如图,过点D作DE⊥AB于点E.
∵EB⊥BC,DC⊥BC,∴四边形BCDE为矩形,
∴DE=BC=9.6 m,BE=DC=2 m.
∵同一时刻物高与影长成比例,∴=,解得AE=8,∴AB=8+2=10(m).
答:旗杆AB的高度为10 m.
19、“创新实践”小组想利用镜子与皮尺测量大树AB的高度,因大树底部有障碍物,无法直接测量到大树底部的距离.聪明的小颖借鉴《海岛算经》的测量方法设计出如图所示的测量方案:测量者站在点F处,将镜子放在点M处时,刚好看到大树的顶端,沿大树方向向前走2.8米,到达点D处,将镜子放在点N处时,刚好看到大树的顶端(点F,M,D,N,B在同一条直线上).若测得FM=1.5米,DN=1.1米,测量者眼睛到地面的距离为1.6米,求大树AB的高度.
【解答】解:设NB的长为x米,则MB=x+1.1+2.8﹣1.5=(x+2.4)米.
由题意,得∠CND=∠ANB,∠CDN=∠ABN=90°,∴△CND∽△ANB,
∴.
同理,△EMF∽△AMB,∴.
∵EF=CD,∴,即.解得x=6.6,
∵,∴.解得AB=9.6.答:大树AB的高度为9.6米.
20、在某一时刻测得一根长为1 m的竹竿的影长为0.8 m,同时测得一棵树落在地面上的影长为2.4 m,落在坡面上的影长为3.2 m(如图),此时身高是1.6 m的小明站在坡面上,影子也都落在坡面上,测得他的影长为2 m.求树的高度.
解:如图,设AB为树的高度,BC为树落在地面上的影子,
CD为树落在坡面上的影子,则BC=2.4 m,CD=3.2 m.
作过点A,C的一束平行光线AD,EC,EC交AB于点E,作CF⊥BC于点C,交AD于点F,易知四边形AECF是平行四边形,∴AE=CF.
由题意得=,解得BE=3 m,=,解得CF=2.56 m,
∴AB=AE+BE=CF+BE=5.56 m. 答:树的高度为5.56 m.
一、选择题
1、在下面的图形中,表示两棵小树在同一时刻阳光下的影子的是 ( )
2、为了加强视力保护意识,小明要在书房里挂一张视力表.由于书房空间狭小,他想根据测试距离为5 m的大视力表制作一个测试距离为3 m的小视力表.如图,如果大视力表中“E”的高度是3.5 cm,那么小视力表中相应“E”的高度是( )
A.3 cm B.2.5 cm C.2.3 cm D.2.1 cm
3、如图是小明测量某古城墙高度的示意图,点P处放一水平的平面镜,然后,后退至点B,从点A经平面镜刚好看到古城墙CD的顶端C处,已知AB⊥BD,CD⊥BD,且测得AB=1.2米,BP=1.8米,PD=12米,那么该古城墙的高度是 ( )
A.6米 B.8米 C.18米 D.24米
4、如图,小明在打网球时,要使球恰好能打过网,而且落在离网5米的位置上,
则球拍击球的高度h应为( )
A.2.7 m B.1.8 m C.0.9 m D.6 m
5、如图,A,B两地被池塘隔开,小明通过下列方法测出了A、B间的距离:先在AB外选一点C,然后测出AC,BC的中点M,N,并测量出MN的长为12m,由此他就知道了A、B间的距离.有关他这次探究活动的描述错误的是( )
A.AB=24m B. MN∥AB C. △CMN∽△CAB D. CM:MA=1:2
6、如图,利用标杆BE测量建筑物的高度.已知标杆BE高1.2 m,测得AB=1.6 m,BC=12.4 m,则建筑物CD的高是( )
A.9.3 m B.10.5 m C.12.4 m D.14 m
7、在同一时刻两根木竿在太阳光下的影子如图所示,其中木竿AB=2 m,它的影子BC=1.6 m,木竿PQ的影子有一部分落在了墙上,PM=1.2 m,MN=0.8 m,则木竿PQ的长度为( )
A.2.3 m B.2.5 m C.2.4 m D.2.1 m
二、填空题
8、小川和爸爸到公园散步,小川的身高是160 cm,爸爸的身高是180 cm,在同一时刻下,小川的影长为80 cm,则此时爸爸的影长为_______cm.
9、如图,上体育课时,甲、乙两名同学分别站在C、D的位置,乙的影子恰好在甲的影子里边,已知甲、乙两同学相距1米.甲身高1.8米,乙身高1.5米,则甲的影长是_______米.
10、某同学想利用相似三角形的有关知识来求一座铁塔的高度.某一时刻,他先测量出铁塔落在地面上的影长为14 m,然后在同一时刻立一根高2 m的标杆,测得标杆影长为0.5 m,
那么铁塔的高度为______m.
11、-天,小青在校园内发现:旁边一棵树在阳光下的影子和她本人的影子在同一直线上,树顶的影子和她头顶的影子恰好落在地面的同一点,同时还发现她站立于树影的中点处(如图所示).如果小青的身高为1.65米,由此可推断出树高为______米.
12、如图是测量河宽的示意图,AE与BC相交于点D,∠B=∠C=90°,测得BD=120 m,DC=60 m,EC=50 m,求得河宽AB=_________m.
13、路边有一根电线杆AB和一块正方形广告牌,有一天,小明突然发现在太阳光照射下,电线杆顶端A的影子刚好落在正方形广告牌的上边中点G处,而正方形广告牌的影子刚好落在地面上的E点处(如图),已知BC=5 m,正方形广告牌的边长为2 m,DE=4 m,则此时电线杆的高度是____m.
14、如图,小明用长为3m的竹竿CD做测量工具,测量学校旗杆AB的高度,移动竹竿,使竹竿与旗杆的距离DB=12m,则旗杆AB的高为 m.
15、如图所示,在阳光下,某一时刻大树AB的影子的顶端落在墙DE上的C点,同一时刻1.2m的标杆影长为3m.已知CD=4m,BD=6m.则大树的高度为 m.
16、如图,AB和DE是直立在地面上的两根立柱,AB=7米,某一时刻AB在阳光下的投影BC=4米,DE在阳光下的投影长为6米,则DE的长为 米.
三、解答题
17、小明想利用阳光下物体的影长测量学校旗杆AB的高度,如图,他在某一时刻在地面上竖立一个2米长的标杆CD,测得其影长DE=0.4米.
(1)请在图中画出此时旗杆AB在地面上的影长BF;
(2)如果BF=1.2米,求旗杆AB的高.
18、如图,某一时刻,旗杆AB的影子一部分在地面上,另一部分在建筑物的墙面上.小丽测得旗杆AB在地面上的影长BC为9.6 m,在墙面上的影长CD为2 m.同一时刻,小丽又测得直立于地面上长1 m的标杆的影长为1.2 m.请你帮助小丽求出旗杆AB的高度.
19、“创新实践”小组想利用镜子与皮尺测量大树AB的高度,因大树底部有障碍物,无法直接测量到大树底部的距离.聪明的小颖借鉴《海岛算经》的测量方法设计出如图所示的测量方案:测量者站在点F处,将镜子放在点M处时,刚好看到大树的顶端,沿大树方向向前走2.8米,到达点D处,将镜子放在点N处时,刚好看到大树的顶端(点F,M,D,N,B在同一条直线上).若测得FM=1.5米,DN=1.1米,测量者眼睛到地面的距离为1.6米,求大树AB的高度.
20、在某一时刻测得一根长为1 m的竹竿的影长为0.8 m,同时测得一棵树落在地面上的影长为2.4 m,落在坡面上的影长为3.2 m(如图),此时身高是1.6 m的小明站在坡面上,影子也都落在坡面上,测得他的影长为2 m.求树的高度.
6.7用相似三角形解决问题(1)-苏科版九年级数学下册 培优训练(答案)
一、选择题
1、在下面的图形中,表示两棵小树在同一时刻阳光下的影子的是 ( D )
2、为了加强视力保护意识,小明要在书房里挂一张视力表.由于书房空间狭小,他想根据测试距离为5 m的大视力表制作一个测试距离为3 m的小视力表.如图,如果大视力表中“E”的高度是3.5 cm,那么小视力表中相应“E”的高度是( )
A.3 cm B.2.5 cm C.2.3 cm D.2.1 cm
[解析] 如图,由题意得CD∥AB,∴=.
∵AB=3.5 cm,BE=5 m,DE=3 m,∴=, ∴CD=2.1 cm.故选D.
3、如图是小明测量某古城墙高度的示意图,点P处放一水平的平面镜,然后,后退至点B,从点A经平面镜刚好看到古城墙CD的顶端C处,已知AB⊥BD,CD⊥BD,且测得AB=1.2米,BP=1.8米,PD=12米,那么该古城墙的高度是 ( B )
A.6米 B.8米 C.18米 D.24米
4、如图,小明在打网球时,要使球恰好能打过网,而且落在离网5米的位置上,
则球拍击球的高度h应为( A )
A.2.7 m B.1.8 m C.0.9 m D.6 m
5、如图,A,B两地被池塘隔开,小明通过下列方法测出了A、B间的距离:先在AB外选一点C,然后测出AC,BC的中点M,N,并测量出MN的长为12m,由此他就知道了A、B间的距离.有关他这次探究活动的描述错误的是( D )
A.AB=24m B. MN∥AB C. △CMN∽△CAB D. CM:MA=1:2
6、如图,利用标杆BE测量建筑物的高度.已知标杆BE高1.2 m,测得AB=1.6 m,BC=12.4 m,则建筑物CD的高是( B )
A.9.3 m B.10.5 m C.12.4 m D.14 m
7、在同一时刻两根木竿在太阳光下的影子如图所示,其中木竿AB=2 m,它的影子BC=1.6 m,木竿PQ的影子有一部分落在了墙上,PM=1.2 m,MN=0.8 m,则木竿PQ的长度为( A )
A.2.3 m B.2.5 m C.2.4 m D.2.1 m
二、填空题
8、小川和爸爸到公园散步,小川的身高是160 cm,爸爸的身高是180 cm,在同一时刻下,小川的影长为80 cm,则此时爸爸的影长为__90______cm.
9、如图,上体育课时,甲、乙两名同学分别站在C、D的位置,乙的影子恰好在甲的影子里边,已知甲、乙两同学相距1米.甲身高1.8米,乙身高1.5米,则甲的影长是__6 _____米.
10、某同学想利用相似三角形的有关知识来求一座铁塔的高度.某一时刻,他先测量出铁塔落在地面上的影长为14 m,然后在同一时刻立一根高2 m的标杆,测得标杆影长为0.5 m,
那么铁塔的高度为____56___m.
11、-天,小青在校园内发现:旁边一棵树在阳光下的影子和她本人的影子在同一直线上,树顶的影子和她头顶的影子恰好落在地面的同一点,同时还发现她站立于树影的中点处(如图所示).如果小青的身高为1.65米,由此可推断出树高为__3.3 _____米.
12、如图是测量河宽的示意图,AE与BC相交于点D,∠B=∠C=90°,测得BD=120 m,DC=60 m,EC=50 m,求得河宽AB=__100 ________m.
13、路边有一根电线杆AB和一块正方形广告牌,有一天,小明突然发现在太阳光照射下,电线杆顶端A的影子刚好落在正方形广告牌的上边中点G处,而正方形广告牌的影子刚好落在地面上的E点处(如图),已知BC=5 m,正方形广告牌的边长为2 m,DE=4 m,则此时电线杆的高度是___5__m.
14、如图,小明用长为3m的竹竿CD做测量工具,测量学校旗杆AB的高度,移动竹竿,使竹竿与旗杆的距离DB=12m,则旗杆AB的高为 9 m.
15、如图所示,在阳光下,某一时刻大树AB的影子的顶端落在墙DE上的C点,同一时刻1.2m的标杆影长为3m.已知CD=4m,BD=6m.则大树的高度为 m.
【解答】解:作CF⊥AB于F,如图,
易得四边形BDCF为矩形,
∴CF=BD=6,BF=CD=4,
∵同一时刻1.2m的标杆影长为3m,
∴=,即=,解得AF=3.2,
∴AB=AF+BF=3.2+4=7.2(m).
故答案为7.2.
16、如图,AB和DE是直立在地面上的两根立柱,AB=7米,某一时刻AB在阳光下的投影BC=4米,DE在阳光下的投影长为6米,则DE的长为 米.
【解答】解:如图所示,
连接AC,过点D作DF∥AC交地面于点F,
∵同一时刻物高与物高的比等于影长与影长的比,∴=,即=
∴DE=.则DE的长为米. 故答案为.
三、解答题
17、小明想利用阳光下物体的影长测量学校旗杆AB的高度,如图,他在某一时刻在地面上竖立一个2米长的标杆CD,测得其影长DE=0.4米.
(1)请在图中画出此时旗杆AB在地面上的影长BF;
(2)如果BF=1.2米,求旗杆AB的高.
解:(1)如图所示.
(2)∵AF∥CE,∴∠AFB=∠CED.
又∵∠ABF=∠CDE=90°,∴△ABF∽△CDE,∴=,解得AB=6米.
答:旗杆AB的高为6米.
18、如图,某一时刻,旗杆AB的影子一部分在地面上,另一部分在建筑物的墙面上.小丽测得旗杆AB在地面上的影长BC为9.6 m,在墙面上的影长CD为2 m.同一时刻,小丽又测得直立于地面上长1 m的标杆的影长为1.2 m.请你帮助小丽求出旗杆AB的高度.
解:如图,过点D作DE⊥AB于点E.
∵EB⊥BC,DC⊥BC,∴四边形BCDE为矩形,
∴DE=BC=9.6 m,BE=DC=2 m.
∵同一时刻物高与影长成比例,∴=,解得AE=8,∴AB=8+2=10(m).
答:旗杆AB的高度为10 m.
19、“创新实践”小组想利用镜子与皮尺测量大树AB的高度,因大树底部有障碍物,无法直接测量到大树底部的距离.聪明的小颖借鉴《海岛算经》的测量方法设计出如图所示的测量方案:测量者站在点F处,将镜子放在点M处时,刚好看到大树的顶端,沿大树方向向前走2.8米,到达点D处,将镜子放在点N处时,刚好看到大树的顶端(点F,M,D,N,B在同一条直线上).若测得FM=1.5米,DN=1.1米,测量者眼睛到地面的距离为1.6米,求大树AB的高度.
【解答】解:设NB的长为x米,则MB=x+1.1+2.8﹣1.5=(x+2.4)米.
由题意,得∠CND=∠ANB,∠CDN=∠ABN=90°,∴△CND∽△ANB,
∴.
同理,△EMF∽△AMB,∴.
∵EF=CD,∴,即.解得x=6.6,
∵,∴.解得AB=9.6.答:大树AB的高度为9.6米.
20、在某一时刻测得一根长为1 m的竹竿的影长为0.8 m,同时测得一棵树落在地面上的影长为2.4 m,落在坡面上的影长为3.2 m(如图),此时身高是1.6 m的小明站在坡面上,影子也都落在坡面上,测得他的影长为2 m.求树的高度.
解:如图,设AB为树的高度,BC为树落在地面上的影子,
CD为树落在坡面上的影子,则BC=2.4 m,CD=3.2 m.
作过点A,C的一束平行光线AD,EC,EC交AB于点E,作CF⊥BC于点C,交AD于点F,易知四边形AECF是平行四边形,∴AE=CF.
由题意得=,解得BE=3 m,=,解得CF=2.56 m,
∴AB=AE+BE=CF+BE=5.56 m. 答:树的高度为5.56 m.
同课章节目录
- 第5章 二次函数
- 5.1 二次函数
- 5.2 二次函数的图象和性质
- 5.3 用待定系数法确定二次函数表达式
- 5.4 二次函数与一元二次方程
- 5.5 用二次函数解决问题
- 第6章 图形的相似
- 6.1 图上距离与实际距离
- 6.2 黄金分割
- 6.3 相似图形
- 6.4 探索三角形相似的条件
- 6.5 相似三角形的性质
- 6.6 图形的位似
- 6.7用相似三角形解决问题
- 第7章 锐角函数
- 7.1 正切
- 7.2 正弦、余弦
- 7.3 特殊角的三角函数
- 7.4 由三角函数值求锐角
- 7.5 解直角三角形
- 7.6 用锐角三角函数解决问题
- 第8章 统计和概率的简单应用
- 8.1 中学生的视力情况调查
- 8.2 货比三家
- 8.3 统计分析帮你做预测
- 8.4 抽签方法合理吗
- 8.5 概率帮你做估计
- 8.6 收取多少保险费合理
