7.4由三角函数值求锐角-苏科版九年级数学下册培优训练(Word版 含答案)
文档属性
| 名称 | 7.4由三角函数值求锐角-苏科版九年级数学下册培优训练(Word版 含答案) |

|
|
| 格式 | doc | ||
| 文件大小 | 1.6MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-12-26 00:00:00 | ||
图片预览

文档简介
7.4由三角函数值求锐角-苏科版九年级数学下册 培优训练
一、选择题
1、若tan α=0.4997,则α约等于( )
A.26°33′5″ B.86°33′4″ C.35°20′3″ D.12°16′4″
2、当∠A为锐角,且<cosA<时,∠A的范围是( )
A.0°<∠A<30° B.30°<∠A<60° C.60°<∠A<90° D.30°<∠A<45°
3、已知cosA·sin30°=,则∠A为( )
A.30° B.45° C.60° D.75°
4、若关于x的方程x2-x+cosα=0有两个相等的实数根,则锐角α的度数为( )
A.30° B.45° C.60° D.75°
5、如果∠α为锐角,且sinα=,那么( )
A.0°<∠α<30° B.30°<∠α<45° C.45°<∠α<60° D.60°<∠α<90°
二、填空题
6、在△ABC中,∠C=90°,a=5,c=13,用计算器求∠A约等于_________
7、利用计算器求下列各角(精确到1′).
(1)sinA=0.75,∠A=______; (2)cosB=0.888 9,∠B=_______;
(3)tanC=45.43,∠C=_______; (4)tanD=0.974 2,∠D=________.
8、如图,在Rt△ABC中,∠C=90°.
(1)若AC=5,BC=12,则AB=______,tanA=_______,∠A≈______(精确到1″);
(2)若AC=3,AB=5,则sinA=______,tanB=______,∠A≈_______,∠B≈______(精确到1″).
9、设α、β为锐角,若sinα=,则α=________;若tanβ=,则β=_________.
10、等腰三角形的底边长为20 cm,面积为 cm2,则顶角为________度.
11、如图,测得一商场自动扶梯的长l为20 m,该自动扶梯到达的高度h为5 m,则自动扶梯与地面所成的角θ的度数是 (精确到1′).
三、解答题
12、若用三根长度分别为8,8,6的木条做成一个等腰三角形,则这个等腰三角形的各个角的大小分别为多少(精确到1′)?
13、已知α、β都是锐角,且cosβ+sinα=1.4538,cosβ-sinα=0.2058,
求∠α和∠β的度数(精确到1″).
14、如图是一晒衣架的侧面示意图,立杆AB,CD相交于点O,B,D两点立于地面,经测量:OE=OF=34 cm,现将晒衣架完全稳固张开,扣链EF成一条线段,且EF=32 cm,求扣链EF与立杆AB的夹角∠OEF的度数(精确到0.1°).
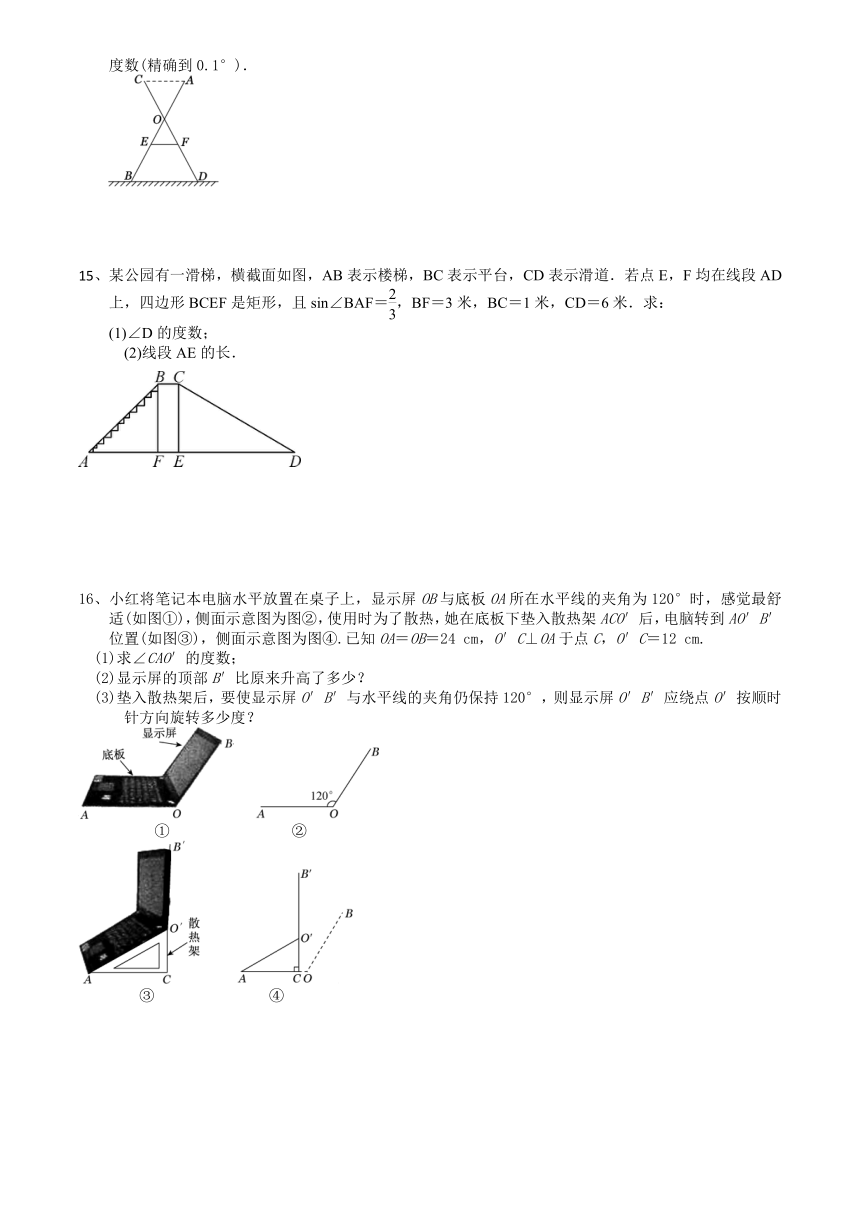
15、某公园有一滑梯,横截面如图,AB表示楼梯,BC表示平台,CD表示滑道.若点E,F均在线段AD上,四边形BCEF是矩形,且sin∠BAF=,BF=3米,BC=1米,CD=6米.求:
(1)∠D的度数;
(2)线段AE的长.
16、小红将笔记本电脑水平放置在桌子上,显示屏OB与底板OA所在水平线的夹角为120°时,感觉最舒适(如图①),侧面示意图为图②,使用时为了散热,她在底板下垫入散热架ACO′后,电脑转到AO′B′位置(如图③),侧面示意图为图④.已知OA=OB=24 cm,O′C⊥OA于点C,O′C=12 cm.
(1)求∠CAO′的度数;
(2)显示屏的顶部B′比原来升高了多少?
(3)垫入散热架后,要使显示屏O′B′与水平线的夹角仍保持120°,则显示屏O′B′应绕点O′按顺时针方向旋转多少度?
① ②
③ ④
7.4由三角函数值求锐角-苏科版九年级数学下册 培优训练(答案)
一、选择题
1、若tan α=0.4997,则α约等于(A )
A.26°33′5″ B.86°33′4″ C.35°20′3″ D.12°16′4″
2、当∠A为锐角,且<cosA<时,∠A的范围是( B )
A.0°<∠A<30° B.30°<∠A<60° C.60°<∠A<90° D.30°<∠A<45°
3、已知cosA·sin30°=,则∠A为( )
A.30° B.45° C.60° D.75°
【解析】 由题意,得cosA×=,∴cosA=,∴∠A=30°.故选A.
4、若关于x的方程x2-x+cosα=0有两个相等的实数根,则锐角α的度数为(C )
A.30° B.45° C.60° D.75°
5、如果∠α为锐角,且sinα=,那么( A )
A.0°<∠α<30° B.30°<∠α<45° C.45°<∠α<60° D.60°<∠α<90°
二、填空题
6、在△ABC中,∠C=90°,a=5,c=13,用计算器求∠A约等于___22°37′ ______
7、利用计算器求下列各角(精确到1′).
(1)sinA=0.75,∠A=______; (2)cosB=0.888 9,∠B=_______;
(3)tanC=45.43,∠C=_______; (4)tanD=0.974 2,∠D=________.
答案:(1)∠A≈48°35′ (2)∠B≈27°16′ (3)∠C≈88°44′ (4)∠D≈44°15′
8、如图,在Rt△ABC中,∠C=90°.
(1)若AC=5,BC=12,则AB=______,tanA=_______,∠A≈______(精确到1″);
(2)若AC=3,AB=5,则sinA=______,tanB=______,∠A≈_______,∠B≈______(精确到1″).
答案: (1)13,,67°22′48″ (2),,53°7′48″,36°52′12″
9、设α、β为锐角,若sinα=,则α=________;若tanβ=,则β=_________.
答案:60°,30°
10、等腰三角形的底边长为20 cm,面积为 cm2,则顶角为________度.
【解析】 如答图,作等腰三角形ABC的高线AD,有BD=BC=10(cm).
又∵BC·AD=, ∴ ×20×AD=,解得AD=,
∴tan∠BAD===, ∴∠BAD=60°,∴∠BAC=120°.
11、如图,测得一商场自动扶梯的长l为20 m,该自动扶梯到达的高度h为5 m,则自动扶梯与地面所成的角θ的度数是14°29′ (精确到1′).
三、解答题
12、若用三根长度分别为8,8,6的木条做成一个等腰三角形,则这个等腰三角形的各个角的大小分别为多少(精确到1′)?
解:如答图,根据题意,作△ABC,AB=AC=8,BC=6.
过点A作AD⊥BC于点D,则BD=CD=3.∴cosB==,
∴∠B≈67°59′, ∴∠C≈67°59′,∠A≈44°2′.
13、已知α、β都是锐角,且cosβ+sinα=1.4538,cosβ-sinα=0.2058,
求∠α和∠β的度数(精确到1″).
答案: 38°36′32″,33°55′18″
14、如图是一晒衣架的侧面示意图,立杆AB,CD相交于点O,B,D两点立于地面,经测量:OE=OF=34 cm,现将晒衣架完全稳固张开,扣链EF成一条线段,且EF=32 cm,求扣链EF与立杆AB的夹角∠OEF的度数(精确到0.1°).
解:如答图,过点O作OM⊥EF于点M,则EM=16 cm.
在Rt△OEM中,∵∠OME=90°,∴cos∠OEF==≈0.470 6,∴∠OEF≈61.9°.
15、某公园有一滑梯,横截面如图,AB表示楼梯,BC表示平台,CD表示滑道.若点E,F均在线段AD上,四边形BCEF是矩形,且sin∠BAF=,BF=3米,BC=1米,CD=6米.求:
(1)∠D的度数;
(2)线段AE的长.
解:(1)∵四边形BCEF是矩形,∴CE=BF=3,CD=6,
由sinD==,∴∠D=30°
(2)在Rt△ABF中,sin∠BAF==,设BF=2k,则AB=3k,
由勾股定理得AF=k.由BF=3,即2k=3,∴k=,
∴AF=,AE=(+1)米
16、小红将笔记本电脑水平放置在桌子上,显示屏OB与底板OA所在水平线的夹角为120°时,感觉最舒适(如图①),侧面示意图为图②,使用时为了散热,她在底板下垫入散热架ACO′后,电脑转到AO′B′位置(如图③),侧面示意图为图④.已知OA=OB=24 cm,O′C⊥OA于点C,O′C=12 cm.
(1)求∠CAO′的度数;
(2)显示屏的顶部B′比原来升高了多少?
(3)垫入散热架后,要使显示屏O′B′与水平线的夹角仍保持120°,则显示屏O′B′应绕点O′按顺时针方向旋转多少度?
① ②
③ ④
解:(1)∵O′C⊥OA,O′C=12 cm,O′A=OA=24 cm, ∴sin∠CAO′===,
∴∠CAO′=30°;
(2)如答图,过点B作BD⊥AC,交AC的延长线于点D.
∵∠BOD=180°-∠AOB=60°,∴BD=24sin60°=12(cm),
又∵B′C=B′O′+O′C=24+12=36(cm),∴B′C-BD= cm,
即显示屏的顶部B′比原来升高了 cm;
(3)∵120°-90°=30°, ∴显示屏O′B′应绕点O′按顺时针方向旋转30°.
一、选择题
1、若tan α=0.4997,则α约等于( )
A.26°33′5″ B.86°33′4″ C.35°20′3″ D.12°16′4″
2、当∠A为锐角,且<cosA<时,∠A的范围是( )
A.0°<∠A<30° B.30°<∠A<60° C.60°<∠A<90° D.30°<∠A<45°
3、已知cosA·sin30°=,则∠A为( )
A.30° B.45° C.60° D.75°
4、若关于x的方程x2-x+cosα=0有两个相等的实数根,则锐角α的度数为( )
A.30° B.45° C.60° D.75°
5、如果∠α为锐角,且sinα=,那么( )
A.0°<∠α<30° B.30°<∠α<45° C.45°<∠α<60° D.60°<∠α<90°
二、填空题
6、在△ABC中,∠C=90°,a=5,c=13,用计算器求∠A约等于_________
7、利用计算器求下列各角(精确到1′).
(1)sinA=0.75,∠A=______; (2)cosB=0.888 9,∠B=_______;
(3)tanC=45.43,∠C=_______; (4)tanD=0.974 2,∠D=________.
8、如图,在Rt△ABC中,∠C=90°.
(1)若AC=5,BC=12,则AB=______,tanA=_______,∠A≈______(精确到1″);
(2)若AC=3,AB=5,则sinA=______,tanB=______,∠A≈_______,∠B≈______(精确到1″).
9、设α、β为锐角,若sinα=,则α=________;若tanβ=,则β=_________.
10、等腰三角形的底边长为20 cm,面积为 cm2,则顶角为________度.
11、如图,测得一商场自动扶梯的长l为20 m,该自动扶梯到达的高度h为5 m,则自动扶梯与地面所成的角θ的度数是 (精确到1′).
三、解答题
12、若用三根长度分别为8,8,6的木条做成一个等腰三角形,则这个等腰三角形的各个角的大小分别为多少(精确到1′)?
13、已知α、β都是锐角,且cosβ+sinα=1.4538,cosβ-sinα=0.2058,
求∠α和∠β的度数(精确到1″).
14、如图是一晒衣架的侧面示意图,立杆AB,CD相交于点O,B,D两点立于地面,经测量:OE=OF=34 cm,现将晒衣架完全稳固张开,扣链EF成一条线段,且EF=32 cm,求扣链EF与立杆AB的夹角∠OEF的度数(精确到0.1°).
15、某公园有一滑梯,横截面如图,AB表示楼梯,BC表示平台,CD表示滑道.若点E,F均在线段AD上,四边形BCEF是矩形,且sin∠BAF=,BF=3米,BC=1米,CD=6米.求:
(1)∠D的度数;
(2)线段AE的长.
16、小红将笔记本电脑水平放置在桌子上,显示屏OB与底板OA所在水平线的夹角为120°时,感觉最舒适(如图①),侧面示意图为图②,使用时为了散热,她在底板下垫入散热架ACO′后,电脑转到AO′B′位置(如图③),侧面示意图为图④.已知OA=OB=24 cm,O′C⊥OA于点C,O′C=12 cm.
(1)求∠CAO′的度数;
(2)显示屏的顶部B′比原来升高了多少?
(3)垫入散热架后,要使显示屏O′B′与水平线的夹角仍保持120°,则显示屏O′B′应绕点O′按顺时针方向旋转多少度?
① ②
③ ④
7.4由三角函数值求锐角-苏科版九年级数学下册 培优训练(答案)
一、选择题
1、若tan α=0.4997,则α约等于(A )
A.26°33′5″ B.86°33′4″ C.35°20′3″ D.12°16′4″
2、当∠A为锐角,且<cosA<时,∠A的范围是( B )
A.0°<∠A<30° B.30°<∠A<60° C.60°<∠A<90° D.30°<∠A<45°
3、已知cosA·sin30°=,则∠A为( )
A.30° B.45° C.60° D.75°
【解析】 由题意,得cosA×=,∴cosA=,∴∠A=30°.故选A.
4、若关于x的方程x2-x+cosα=0有两个相等的实数根,则锐角α的度数为(C )
A.30° B.45° C.60° D.75°
5、如果∠α为锐角,且sinα=,那么( A )
A.0°<∠α<30° B.30°<∠α<45° C.45°<∠α<60° D.60°<∠α<90°
二、填空题
6、在△ABC中,∠C=90°,a=5,c=13,用计算器求∠A约等于___22°37′ ______
7、利用计算器求下列各角(精确到1′).
(1)sinA=0.75,∠A=______; (2)cosB=0.888 9,∠B=_______;
(3)tanC=45.43,∠C=_______; (4)tanD=0.974 2,∠D=________.
答案:(1)∠A≈48°35′ (2)∠B≈27°16′ (3)∠C≈88°44′ (4)∠D≈44°15′
8、如图,在Rt△ABC中,∠C=90°.
(1)若AC=5,BC=12,则AB=______,tanA=_______,∠A≈______(精确到1″);
(2)若AC=3,AB=5,则sinA=______,tanB=______,∠A≈_______,∠B≈______(精确到1″).
答案: (1)13,,67°22′48″ (2),,53°7′48″,36°52′12″
9、设α、β为锐角,若sinα=,则α=________;若tanβ=,则β=_________.
答案:60°,30°
10、等腰三角形的底边长为20 cm,面积为 cm2,则顶角为________度.
【解析】 如答图,作等腰三角形ABC的高线AD,有BD=BC=10(cm).
又∵BC·AD=, ∴ ×20×AD=,解得AD=,
∴tan∠BAD===, ∴∠BAD=60°,∴∠BAC=120°.
11、如图,测得一商场自动扶梯的长l为20 m,该自动扶梯到达的高度h为5 m,则自动扶梯与地面所成的角θ的度数是14°29′ (精确到1′).
三、解答题
12、若用三根长度分别为8,8,6的木条做成一个等腰三角形,则这个等腰三角形的各个角的大小分别为多少(精确到1′)?
解:如答图,根据题意,作△ABC,AB=AC=8,BC=6.
过点A作AD⊥BC于点D,则BD=CD=3.∴cosB==,
∴∠B≈67°59′, ∴∠C≈67°59′,∠A≈44°2′.
13、已知α、β都是锐角,且cosβ+sinα=1.4538,cosβ-sinα=0.2058,
求∠α和∠β的度数(精确到1″).
答案: 38°36′32″,33°55′18″
14、如图是一晒衣架的侧面示意图,立杆AB,CD相交于点O,B,D两点立于地面,经测量:OE=OF=34 cm,现将晒衣架完全稳固张开,扣链EF成一条线段,且EF=32 cm,求扣链EF与立杆AB的夹角∠OEF的度数(精确到0.1°).
解:如答图,过点O作OM⊥EF于点M,则EM=16 cm.
在Rt△OEM中,∵∠OME=90°,∴cos∠OEF==≈0.470 6,∴∠OEF≈61.9°.
15、某公园有一滑梯,横截面如图,AB表示楼梯,BC表示平台,CD表示滑道.若点E,F均在线段AD上,四边形BCEF是矩形,且sin∠BAF=,BF=3米,BC=1米,CD=6米.求:
(1)∠D的度数;
(2)线段AE的长.
解:(1)∵四边形BCEF是矩形,∴CE=BF=3,CD=6,
由sinD==,∴∠D=30°
(2)在Rt△ABF中,sin∠BAF==,设BF=2k,则AB=3k,
由勾股定理得AF=k.由BF=3,即2k=3,∴k=,
∴AF=,AE=(+1)米
16、小红将笔记本电脑水平放置在桌子上,显示屏OB与底板OA所在水平线的夹角为120°时,感觉最舒适(如图①),侧面示意图为图②,使用时为了散热,她在底板下垫入散热架ACO′后,电脑转到AO′B′位置(如图③),侧面示意图为图④.已知OA=OB=24 cm,O′C⊥OA于点C,O′C=12 cm.
(1)求∠CAO′的度数;
(2)显示屏的顶部B′比原来升高了多少?
(3)垫入散热架后,要使显示屏O′B′与水平线的夹角仍保持120°,则显示屏O′B′应绕点O′按顺时针方向旋转多少度?
① ②
③ ④
解:(1)∵O′C⊥OA,O′C=12 cm,O′A=OA=24 cm, ∴sin∠CAO′===,
∴∠CAO′=30°;
(2)如答图,过点B作BD⊥AC,交AC的延长线于点D.
∵∠BOD=180°-∠AOB=60°,∴BD=24sin60°=12(cm),
又∵B′C=B′O′+O′C=24+12=36(cm),∴B′C-BD= cm,
即显示屏的顶部B′比原来升高了 cm;
(3)∵120°-90°=30°, ∴显示屏O′B′应绕点O′按顺时针方向旋转30°.
同课章节目录
- 第5章 二次函数
- 5.1 二次函数
- 5.2 二次函数的图象和性质
- 5.3 用待定系数法确定二次函数表达式
- 5.4 二次函数与一元二次方程
- 5.5 用二次函数解决问题
- 第6章 图形的相似
- 6.1 图上距离与实际距离
- 6.2 黄金分割
- 6.3 相似图形
- 6.4 探索三角形相似的条件
- 6.5 相似三角形的性质
- 6.6 图形的位似
- 6.7用相似三角形解决问题
- 第7章 锐角函数
- 7.1 正切
- 7.2 正弦、余弦
- 7.3 特殊角的三角函数
- 7.4 由三角函数值求锐角
- 7.5 解直角三角形
- 7.6 用锐角三角函数解决问题
- 第8章 统计和概率的简单应用
- 8.1 中学生的视力情况调查
- 8.2 货比三家
- 8.3 统计分析帮你做预测
- 8.4 抽签方法合理吗
- 8.5 概率帮你做估计
- 8.6 收取多少保险费合理
