金属晶体的堆积模型
图片预览



文档简介
(共17张PPT)
第三节 金属晶体
第2课时 金属晶体的原子 堆积模型
成都市川化中学 张亚军
2
5
6
4
3
7
8
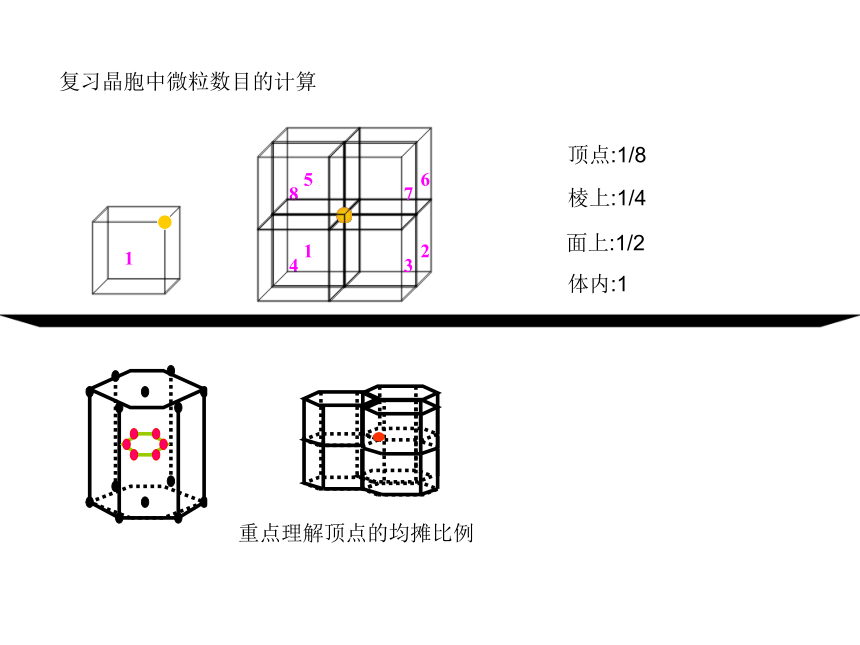
复习晶胞中微粒数目的计算
1
1
顶点:1/8
棱上:1/4
面上:1/2
体内:1
重点理解顶点的均摊比例
自学并小组学习讨论
【要求】 认识理解并能分清楚在平面上金属原子排列的非密置层和密置层。
【回答】非密置层堆积与密置层堆积的方式有什么不同?
【亲自体验活动】用桌上的乒乓球堆积出非密置层和密置层,并在模型图上
任选一个中心原子标出它周围的配位原子及配位数
行列对齐四原子围一空 非最紧密排列
行列相错三原子围一空最紧密排列
【学生活动】探究金属原子在二维平面上有几种排列方式?
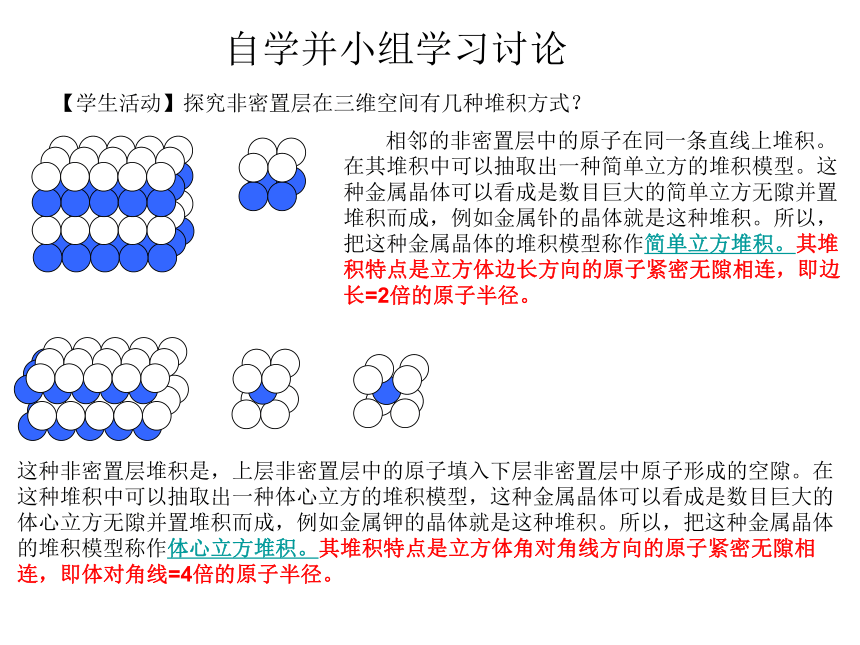
【学生活动】探究非密置层在三维空间有几种堆积方式?
自学并小组学习讨论
相邻的非密置层中的原子在同一条直线上堆积。
在其堆积中可以抽取出一种简单立方的堆积模型。这
种金属晶体可以看成是数目巨大的简单立方无隙并置
堆积而成,例如金属钋的晶体就是这种堆积。所以,
把这种金属晶体的堆积模型称作简单立方堆积。其堆
积特点是立方体边长方向的原子紧密无隙相连,即边
长=2倍的原子半径。
这种非密置层堆积是,上层非密置层中的原子填入下层非密置层中原子形成的空隙。在
这种堆积中可以抽取出一种体心立方的堆积模型,这种金属晶体可以看成是数目巨大的体心立方无隙并置堆积而成,例如金属钾的晶体就是这种堆积。所以,把这种金属晶体的堆积模型称作体心立方堆积。其堆积特点是立方体角对角线方向的原子紧密无隙相连,即体对角线=4倍的原子半径。
【学生活动】探究密置层在三维空间有几种堆积方式?
自学并小组学习讨论
第三层对准第一层的原子重复堆积,于是每两层形成一个周期,即ABABAB......堆积方式。在其堆积
中可以抽取出一种六方最密的堆积模型。所以,把这种金属晶体的堆积模型称作六方最密的堆积。
第三层原子对准第一层的与第二层共同形成的空隙堆积,于是每三层形成一个周期,即ABCABCABC.....堆积方式。在其堆积中可以抽取出一种面心方最密的堆积模型。所以,把这种金属晶体的堆积模型称作面心立方最密的堆积。
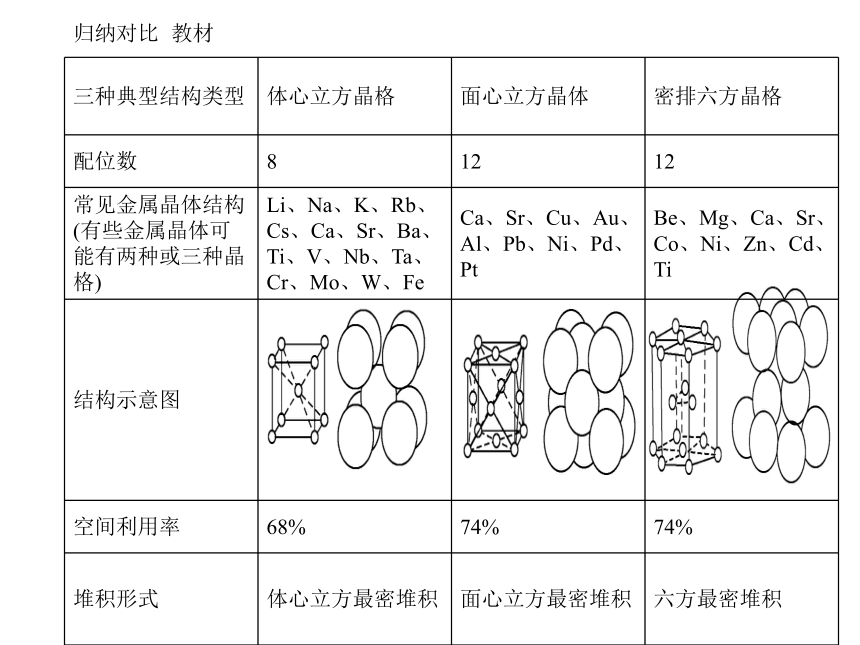
归纳对比 教材
三种典型结构类型 体心立方晶格 面心立方晶体 密排六方晶格
配位数 8 12 12
常见金属晶体结构(有些金属晶体可能有两种或三种晶格) Li、Na、K、Rb、Cs、Ca、Sr、Ba、Ti、V、Nb、Ta、Cr、Mo、W、Fe Ca、Sr、Cu、Au、Al、Pb、Ni、Pd、Pt Be、Mg、Ca、Sr、Co、Ni、Zn、Cd、Ti
结构示意图
空间利用率 68% 74% 74%
堆积形式 体心立方最密堆积 面心立方最密堆积 六方最密堆积
课堂练习
1.只有阳离子而没有阴离子的晶体是( )
A.金属晶体 B.原子晶体 C.离子晶体 D.分子晶体
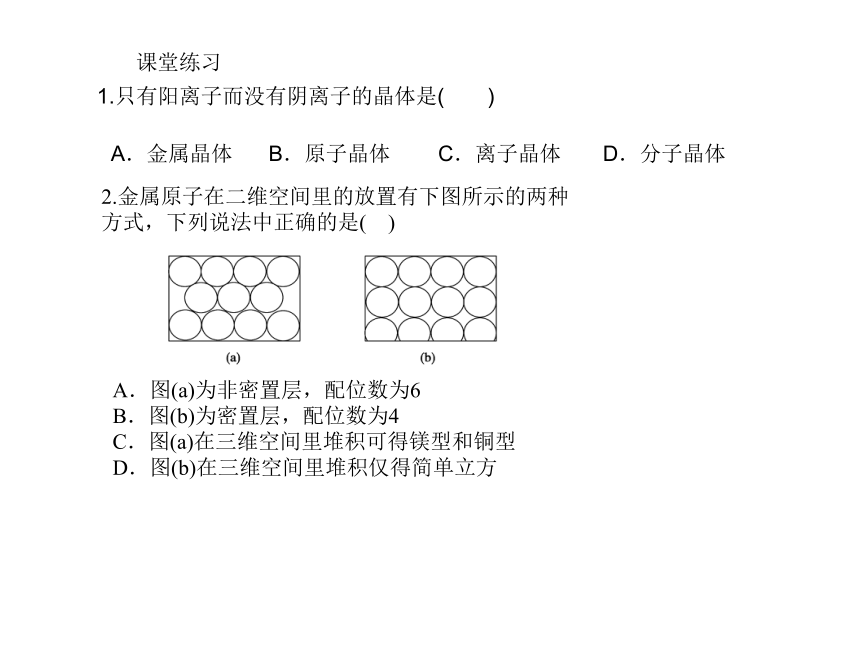
2.金属原子在二维空间里的放置有下图所示的两种
方式,下列说法中正确的是( )
A.图(a)为非密置层,配位数为6
B.图(b)为密置层,配位数为4
C.图(a)在三维空间里堆积可得镁型和铜型
D.图(b)在三维空间里堆积仅得简单立方
答案 3.59×10-10
3.晶胞即晶体中最小的重复单元。已知铜为面心立方晶体,其结构如图Ⅰ所示,
面心立方的结构特征如图Ⅱ所示。若铜原子的半径为1.27×10-10 m,试求铜金
属晶体中的晶胞边长,即图Ⅲ中AB的长度为______m。
4.金晶体的最小重复单元(也称晶胞)是面心立方体,即在立方体的8个
顶点各有一个金原子,各个面的中心有一个金原子,每个金原子被
相邻的晶胞所共有。金原子的直径为d,用NA表示阿伏加德罗常数,
M表示金的摩尔质量。
(1)金晶体每个晶胞中含有 个金原子。
(2)欲计算一个晶胞的体积,除假定金原子是刚性小球外,还应假定 。
(3)一个晶胞的体积是 。
(4)金晶体的密度是 。
[课后思考题]
5.已知金属铜为面心立方晶体,如图所示,铜的相对原子质量为63.54,密度为 8.936g/cm3,试求
(1)图中正方形边长 a,
(2)铜的金属半径 r
a
r
r
o
r
r
自我评价
1.是否能够用自己的语言向同学或老师描述出金属晶体内原子的四种
堆积模型的抽取来历吗?
2.能说出四种堆积模型中原子半径与边长,面对角线,体对角线的关系吗?
金属晶体的四种堆积模型
简单立方堆积【学与练】
【描述】这种晶胞模型是从那种排列方式中抽取出来的?
配位数是多少?指出配位原子及配位数
【小组学习讨论】
【1】边长a与原子半径r的关系:
【2】面对角线与原子半径r的关系:
【3】体对角线与原子半径r的关系:
【4】空间利用率
a=2r
面对角线=
体对角线=
边长方向两个原子紧密排列,
其他方向的原子没有紧密排列
返回
体心立方堆积模型【学与练】
【问题】这种晶胞模型是从那种排列方式中抽取出来的?怎么抽取?
配位数是多少?指出配位原子及配位数
体对角线方向两个原子紧密排列,
其他方向的原子没有紧密排列
【小组学习讨论】
【1】体对角线与原子半径r的关系:
【2】边长a与原子半径r的关系:
【3】面对角线与原子半径r的关系:
【4】空间利用率
体对角线=4r
边长a=
面对角线=
金属晶体的四种堆积模型
返回
六方最密堆积模型
【问题】这种晶胞模型是从那种排列方式中抽取出来的?怎么抽取?
配位数是多少?指出配位原子及配位数。
金属晶体的四种堆积模型
返回
【思考】第2层分别与第1层第3层所形成的空隙
是否相同?
面心立方最密堆积模型【学与练】
【问题】这种晶胞模型是从那种排列方式中抽取出来的?怎么抽取?
配位数是多少?指出配位原子及配位数
【小组学习讨论】
【1】面对角线与原子半径r的关系:
【2】边长a与原子半径r的关系:
【3】体对角线与原子半径r的关系:
【4】空间利用率
面对角线=4r
面对角线方向两个原子紧密排列,
其他方向的原子没有紧密排列
金属晶体的四种堆积模型
返回
【思考】第2层分别与第1层第3层所形成的空隙是否相同?
谢谢
第三节 金属晶体
第2课时 金属晶体的原子 堆积模型
成都市川化中学 张亚军
2
5
6
4
3
7
8
复习晶胞中微粒数目的计算
1
1
顶点:1/8
棱上:1/4
面上:1/2
体内:1
重点理解顶点的均摊比例
自学并小组学习讨论
【要求】 认识理解并能分清楚在平面上金属原子排列的非密置层和密置层。
【回答】非密置层堆积与密置层堆积的方式有什么不同?
【亲自体验活动】用桌上的乒乓球堆积出非密置层和密置层,并在模型图上
任选一个中心原子标出它周围的配位原子及配位数
行列对齐四原子围一空 非最紧密排列
行列相错三原子围一空最紧密排列
【学生活动】探究金属原子在二维平面上有几种排列方式?
【学生活动】探究非密置层在三维空间有几种堆积方式?
自学并小组学习讨论
相邻的非密置层中的原子在同一条直线上堆积。
在其堆积中可以抽取出一种简单立方的堆积模型。这
种金属晶体可以看成是数目巨大的简单立方无隙并置
堆积而成,例如金属钋的晶体就是这种堆积。所以,
把这种金属晶体的堆积模型称作简单立方堆积。其堆
积特点是立方体边长方向的原子紧密无隙相连,即边
长=2倍的原子半径。
这种非密置层堆积是,上层非密置层中的原子填入下层非密置层中原子形成的空隙。在
这种堆积中可以抽取出一种体心立方的堆积模型,这种金属晶体可以看成是数目巨大的体心立方无隙并置堆积而成,例如金属钾的晶体就是这种堆积。所以,把这种金属晶体的堆积模型称作体心立方堆积。其堆积特点是立方体角对角线方向的原子紧密无隙相连,即体对角线=4倍的原子半径。
【学生活动】探究密置层在三维空间有几种堆积方式?
自学并小组学习讨论
第三层对准第一层的原子重复堆积,于是每两层形成一个周期,即ABABAB......堆积方式。在其堆积
中可以抽取出一种六方最密的堆积模型。所以,把这种金属晶体的堆积模型称作六方最密的堆积。
第三层原子对准第一层的与第二层共同形成的空隙堆积,于是每三层形成一个周期,即ABCABCABC.....堆积方式。在其堆积中可以抽取出一种面心方最密的堆积模型。所以,把这种金属晶体的堆积模型称作面心立方最密的堆积。
归纳对比 教材
三种典型结构类型 体心立方晶格 面心立方晶体 密排六方晶格
配位数 8 12 12
常见金属晶体结构(有些金属晶体可能有两种或三种晶格) Li、Na、K、Rb、Cs、Ca、Sr、Ba、Ti、V、Nb、Ta、Cr、Mo、W、Fe Ca、Sr、Cu、Au、Al、Pb、Ni、Pd、Pt Be、Mg、Ca、Sr、Co、Ni、Zn、Cd、Ti
结构示意图
空间利用率 68% 74% 74%
堆积形式 体心立方最密堆积 面心立方最密堆积 六方最密堆积
课堂练习
1.只有阳离子而没有阴离子的晶体是( )
A.金属晶体 B.原子晶体 C.离子晶体 D.分子晶体
2.金属原子在二维空间里的放置有下图所示的两种
方式,下列说法中正确的是( )
A.图(a)为非密置层,配位数为6
B.图(b)为密置层,配位数为4
C.图(a)在三维空间里堆积可得镁型和铜型
D.图(b)在三维空间里堆积仅得简单立方
答案 3.59×10-10
3.晶胞即晶体中最小的重复单元。已知铜为面心立方晶体,其结构如图Ⅰ所示,
面心立方的结构特征如图Ⅱ所示。若铜原子的半径为1.27×10-10 m,试求铜金
属晶体中的晶胞边长,即图Ⅲ中AB的长度为______m。
4.金晶体的最小重复单元(也称晶胞)是面心立方体,即在立方体的8个
顶点各有一个金原子,各个面的中心有一个金原子,每个金原子被
相邻的晶胞所共有。金原子的直径为d,用NA表示阿伏加德罗常数,
M表示金的摩尔质量。
(1)金晶体每个晶胞中含有 个金原子。
(2)欲计算一个晶胞的体积,除假定金原子是刚性小球外,还应假定 。
(3)一个晶胞的体积是 。
(4)金晶体的密度是 。
[课后思考题]
5.已知金属铜为面心立方晶体,如图所示,铜的相对原子质量为63.54,密度为 8.936g/cm3,试求
(1)图中正方形边长 a,
(2)铜的金属半径 r
a
r
r
o
r
r
自我评价
1.是否能够用自己的语言向同学或老师描述出金属晶体内原子的四种
堆积模型的抽取来历吗?
2.能说出四种堆积模型中原子半径与边长,面对角线,体对角线的关系吗?
金属晶体的四种堆积模型
简单立方堆积【学与练】
【描述】这种晶胞模型是从那种排列方式中抽取出来的?
配位数是多少?指出配位原子及配位数
【小组学习讨论】
【1】边长a与原子半径r的关系:
【2】面对角线与原子半径r的关系:
【3】体对角线与原子半径r的关系:
【4】空间利用率
a=2r
面对角线=
体对角线=
边长方向两个原子紧密排列,
其他方向的原子没有紧密排列
返回
体心立方堆积模型【学与练】
【问题】这种晶胞模型是从那种排列方式中抽取出来的?怎么抽取?
配位数是多少?指出配位原子及配位数
体对角线方向两个原子紧密排列,
其他方向的原子没有紧密排列
【小组学习讨论】
【1】体对角线与原子半径r的关系:
【2】边长a与原子半径r的关系:
【3】面对角线与原子半径r的关系:
【4】空间利用率
体对角线=4r
边长a=
面对角线=
金属晶体的四种堆积模型
返回
六方最密堆积模型
【问题】这种晶胞模型是从那种排列方式中抽取出来的?怎么抽取?
配位数是多少?指出配位原子及配位数。
金属晶体的四种堆积模型
返回
【思考】第2层分别与第1层第3层所形成的空隙
是否相同?
面心立方最密堆积模型【学与练】
【问题】这种晶胞模型是从那种排列方式中抽取出来的?怎么抽取?
配位数是多少?指出配位原子及配位数
【小组学习讨论】
【1】面对角线与原子半径r的关系:
【2】边长a与原子半径r的关系:
【3】体对角线与原子半径r的关系:
【4】空间利用率
面对角线=4r
面对角线方向两个原子紧密排列,
其他方向的原子没有紧密排列
金属晶体的四种堆积模型
返回
【思考】第2层分别与第1层第3层所形成的空隙是否相同?
谢谢
