人教版七年级数学下册 5.2 平行线及其判定 同步测试题(Word版 含解析)
文档属性
| 名称 | 人教版七年级数学下册 5.2 平行线及其判定 同步测试题(Word版 含解析) |  | |
| 格式 | docx | ||
| 文件大小 | 219.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-12-25 22:43:11 | ||
图片预览


文档简介
10312400103378005.2 平行线及其判定 同步测试题
班级:_____________姓名:_____________
一、 选择题 (本题共计 10 小题 ,每题 3 分 ,共计30分 , ) ?
1. 在同一平面内,两直线可能的位置关系是( )
A.相交 B.平行
C.相交或平行 D.相交、平行或垂直?
2. 同一平面内有三条直线,如果其中只有两条平行,那么它们( )
A.没有交点 B.有一个交点 C.有两个交点 D.有三个交点?
3. 下列说法不正确的是( )
A.过马路的斑马线是平行线
B.100米跑道的跑道线是平行线
C.若a?//?b,b?//?d,则a⊥d
D.过直线外一点有且只有一条直线与已知直线平行?
4. 在同一平面内,两条直线的位置关系是( )
A.平行或垂直 B.平行或相交
C.垂直或相交 D.平行、垂直或相交?
5. 如图,点E在BC的延长线上,下列条件中不能判定AB?//?CD的是(? ? ? ? )
?
A.∠3=∠4 B.∠1=∠2
C.∠B=∠DCE D.∠D+∠DAB=180?
?6. 如图,下列四组条件中,能说明AB?//?CD的是(? ? ? ? )
A.∠1=∠2 B.∠BAD=∠BCD
C.∠ABC=∠ADC,∠3=∠4 D.∠BAD+∠ABC=180?
7. 已知同一平面内的三条直线a,b,c,下列命题中错误的是( )
A.∵ a?//?b,b?//?c,∴ a?//?c B.∵ a⊥b,b⊥c,∴ a?//?c
C.∵ a?//?b,b⊥c,∴ a⊥c D.∵ a⊥b,b⊥c,∴ a⊥c?
8. 下列说法正确的是(? ? ? ? )
①在同一平面内,不相交的两条直线叫做平行线;
②在同一平面内,过一点有且仅有一条直线与已知直线平行;
③平面内,过一点有且仅有一条直线与已知直线垂直;
④平行于同一条直线的两条直线平行;
A.①② B.①③ C.①②③ D.①③④?
9. 下列结论正确的是( )
A.不相交的两条直线叫做平行线
B.两条直线被第三条直线所截,同位角相等
C.垂直于同一直线的两条直线互相平行
D.平行于同一直线的两条直线互相平行?
10. 下列说法中,正确的个数为( )
(1)过一点有无数条直线与已知直线平行
(2)如果a?//?b,a?//?c,那么b?//?c
(3)如果两线段不相交,那么它们就平行
(4)如果两直线不相交,那么它们就平行
A.1个 B.2个 C.3个 D.4个
二、 填空题 (本题共计 10 小题 ,每题 3 分 ,共计30分 , ) ?
11. 若AB?//?CD,AB?//?EF,则________. ?
12. 在同一平面内的三条直线,其中有两条直线平行,则这第三条直线的交点一定有两个________.
?
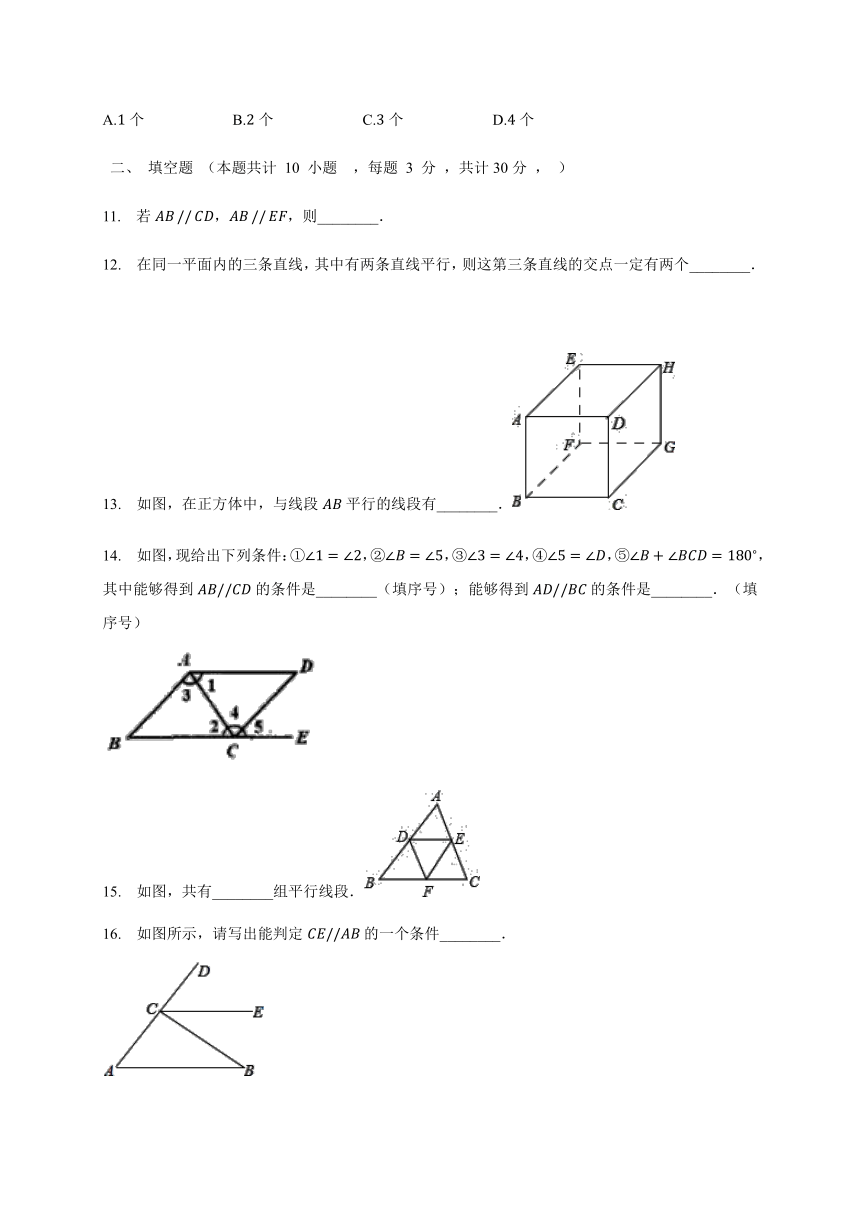
13. 如图,在正方体中,与线段AB平行的线段有________. ?
14. 如图,现给出下列条件:①∠1=∠2,②∠B=∠5,③∠3=∠4,④∠5=∠D,⑤∠B+∠BCD=180?,其中能够得到AB//CD的条件是________(填序号);能够得到AD//BC的条件是________.(填序号)
?
15. 如图,共有________组平行线段. ?
16. 如图所示,请写出能判定CE//AB的一个条件________.
?17. 如果两条直线都与第三条直线平行,那么这两条直线________.也叫做平行线的传递性. ?
18. 下列说法中:
(1)不相交的两条直线叫做平行线; (2)经过一点,有且只有一条直线与已知直线平行;
(3)垂直于同一条直线的两直线平行; (4)直线a?//?b,b?//?c,则a?//?c;
(5)两条直线被第三条直线所截,同位角相等.其中正确的是________.
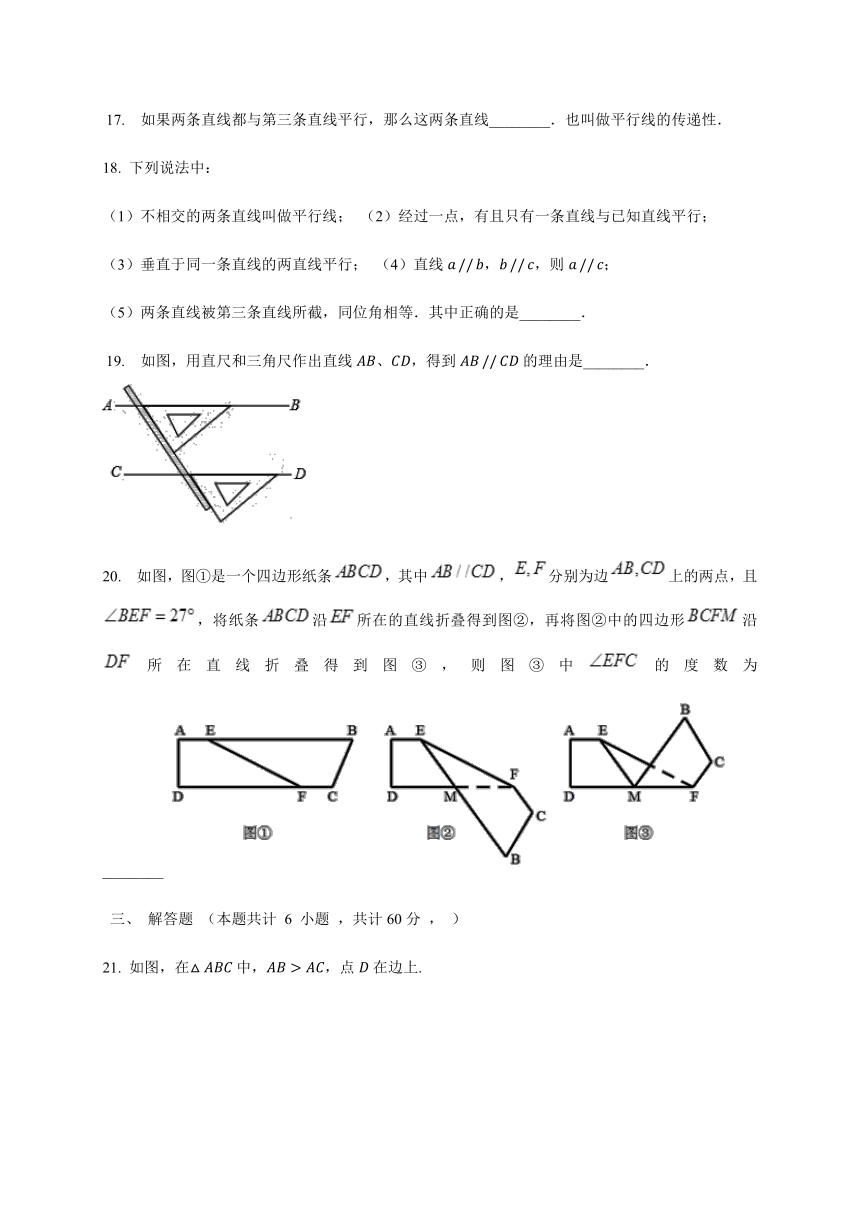
?19. 如图,用直尺和三角尺作出直线AB、CD,得到AB?//?CD的理由是________.
?
20. 如图,图①是一个四边形纸条,其中,分别为边上的两点,且,将纸条沿所在的直线折叠得到图②,再将图②中的四边形沿所在直线折叠得到图③,则图③中的度数为________
三、 解答题 (本题共计 6 小题 ,共计60分 , )
21. 如图,在△ABC中,AB>AC,点D在边上.
(1)过点D,作平行线DE//BC,交AC于点E.(尺规作图,不写作法,保留作图痕迹)
(2)在上(1)中,若∠B=50?,∠A=60?,求∠ADE的度数.
?
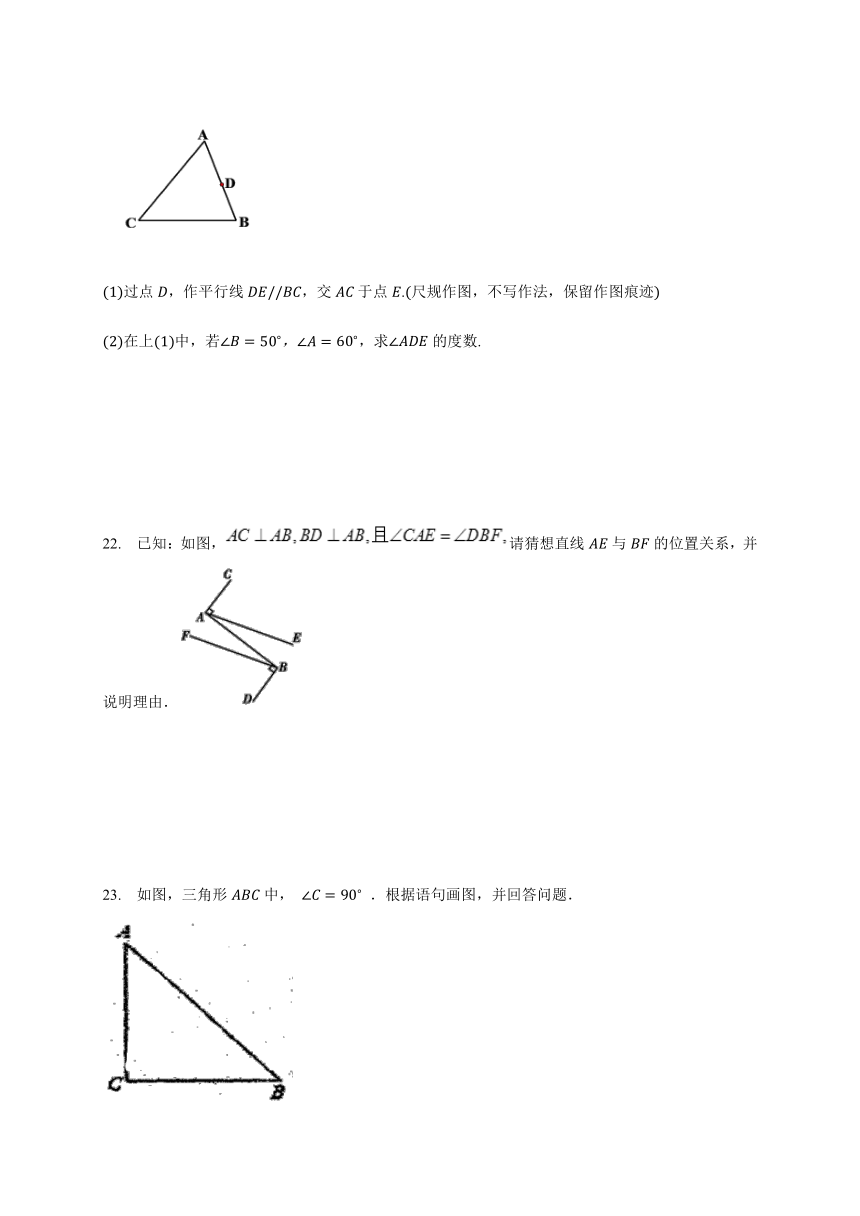
22. 已知:如图,请猜想直线AE与BF的位置关系,并说明理由.
?
23. 如图,三角形ABC中, ∠C=90? .根据语句画图,并回答问题.
(1)过点C画AB的垂线,交AB于点D;
(2)过点A画AE//CB;
(3)三条边AB,AC,BC中哪条边最长?为什么?
?
24. 如图,在四边形ABCD中,∠A=∠B,CB=CE.求证:CE?//?AD.
?
25. 已知:如图,在△AOB中∠O=90?,∠A=50?.
(1)根据下列语句画图:过点O作OC⊥AB,垂足为C,过点C作CD∥OA交OB于点D;
(2)求(1)中作出图中的∠COB的度数;
(3)将(1)中作出图中的△COD绕点O按每秒10?的速度沿顺时针方向旋转一周,当旋转________秒时(直接写结果边OC恰好与边AB平行.
?26. 如图,直线a⊥b,垂足为O,△ABC与直线a、b分别交于点E、F,且∠C=90?,EG、FH分别平分∠MEC和∠NFC.
(1)填空:∠OEC+∠OFC=________;
(2)求证:EG?//?FH.
参考答案
一、 选择题 (本题共计 10 小题 ,每题 3 分 ,共计30分 )
1.
【答案】
C
【解答】
解:平面内,两直线的位置关系是相交或平行(其中,垂直是相交的特例).
故选C.
2.
【答案】
C
【解答】
解:根据题意,第三条直线与这两条平行直线各有一个交点.
故选:C.
3.
【答案】
C
【解答】
解:A,B,由平行线的定义可知,斑马线是平行线,100米跑道的跑道线是平行线,A,B正确;
C,根据平行于同一条直线的两直线平行可知,C错误;
D,过直线外一点有且只有一条直线与已知直线平行,这是平行公理,D正确.
故选C.
4.
【答案】
B
【解答】
解:在同一个平面内,两条直线只有两种位置关系,即平行或相交,
故选:B.
5.
【答案】
A
【解答】
解:A,∠3与∠4是直线AD,BC被AC所截形成的内错角,因为∠3=∠4,所以应是AD?//?BC,故A符合题意;
B,∵ ∠1=∠2,∴ AB?//?CD?(内错角相等,两直线平行),故B不符合题意;
C,∵ ∠DCE=∠B,∴ AB?//?CD?(同位角相等,两直线平行),故C不符合题意;
D,∵ ∠D+∠DAB=180?,∴ AB?//?CD(同旁内角互补,两直线平行),故D不符合题意.
故选A.
6.
【答案】
C
【解答】
解:A、根据∠1=∠2能推出AD//BC,不能推出AB?//?CD,故本选项不符合题意;
B、根据∠BAD=∠BCD不能推出AB?//?CD,故本选项不符合题意;
C、根据∠ABC=∠ADC,∠3=∠4,则∠ABD=∠CDB,能推出AB?//?CD,故本选项符合题意;
D、根据∠BAD+∠ABC=180?能推出AD//BC,不能推出AB?//?CD,故本选项不符合题意.
故选C.
7.
【答案】
D
【解答】
解:A、如果a?//?b,b?//?c,那么a?//?c,正确;
B、如果a⊥b,b⊥c,那么a?//?c,正确;
C、如果a?//?b,b⊥c,那么a⊥c,正确;
D、如果a⊥b,b⊥c,那么a?//?c,错误.
故选:D.
8.
【答案】
D
【解答】
解:①在同一平面内,不相交的两条直线叫做平行线,正确;
②在同一平面内,过一点有且仅有一条直线与已知直线平行,错误,应该是过直线外一点有且仅有一条直线平行于已知直线;
③平面内,过一点有且仅有一条直线与已知直线垂直,正确;
④平行于同一条直线的两条直线平行,正确.
故选D.
9.
【答案】
D
【解答】
解:A、在同一平面内,不相交的两条直线叫做平行线,故A不符合题意;
B、两直线平行,同位角相等,故B不符合题意;
C、在同一平面内,垂直于同一条直线的两条直线互相平行,故C不符合题意;
D、平行于同一直线的两条直线互相平行,故D符合题意;
故选:D.
10.
【答案】
A
【解答】
解:(1)过直线外一点有且只有一条直线与已知直线平行,故错误;
(2)根据平行公理的推论,正确;
(3)线段的长度是有限的,不相交也不一定平行,故错误;
(4)应该是“在同一平面内”,故错误.
正确的只有一个,故选A.
二、 填空题 (本题共计 10 小题 ,每题 3 分 ,共计30分 )
11.
【答案】
CD?//?EF
【解答】
解:根据平行线的传递性,得CD?//?EF.
故答案为CD?//?EF.
12.
【答案】
×
【解答】
解:∵ 如果第三条直线与这两条直线平行则这三条直线没有交点.
∴ 错误.
13.
【答案】
EF、HG、DC
【解答】
解:与AB平行的线段是:DC、EF;
与CD平行的线段是:HG,
所以与AB线段平行的线段有:EF、HG、DC.
故答案是:EF、HG、DC.
14.
【答案】
②③⑤,①④
【解答】
解:能够得到AB//CD的条件是②③⑤.
②∠B=∠5,同位角相等,两直线平行;
③∠3=∠4,内错角相等,两直线平行;
⑤∠B+∠BCD=180?,同旁内角互补,两直线平行.
能够得到AD//BC的条件是①④.
①∠1=∠2,内错角相等,两直线平行;
④∠5=∠D,内错角相等,两直线平行.
故答案为:②③⑤;①④.
15.
【答案】
9
【解答】
解:图中的平行线段有AD?//?EF;BD?//?EF;DE?//?FB;DE?//?FC;DF?//?AE;DF?//?EC;DE?//?BC;DF?//?AC;EF?//?AB.共有9对.
故答案为:9.
16.
【答案】
∠DCE=∠A(答案不唯一)
【解答】
解:能判定CE?//?AB的一个条件是:
∠DCE=∠A或∠ECB=∠B或∠A+∠ACE=180?.
故答案为:∠DCE=∠A(答案不唯一).
17.
【答案】
互相平行
【解答】
解:如果两条直线都与第三条直线平行,那么这两条直线互相平行,也叫做平行线的传递性.
故答案为:互相平行.
18.
【答案】
解:(1)在同一平面内,不相交的两条直线叫做平行线;故错误;
(2)经过直线外一点,有且只有一条直线与已知直线平行;故错误;
(3)在同一平面内,垂直于同一条直线的两直线平行;故错误;
(4)直线a?//?b,b?//?c,则a?//?c;故正确;
(5)两条平行直线被第三条直线所截,同位角相等,故错误.
其中正确的是(4).
【解答】
解:(1)在同一平面内,不相交的两条直线叫做平行线;故错误;
(2)经过直线外一点,有且只有一条直线与已知直线平行;故错误;
(3)在同一平面内,垂直于同一条直线的两直线平行;故错误;
(4)直线a?//?b,b?//?c,则a?//?c;故正确;
(5)两条平行直线被第三条直线所截,同位角相等,故错误.
其中正确的是(4).
19.
【答案】
同位角相等,两直线平行
【解答】
用直尺和三角尺作出直线AB、CD,得到AB?//?CD的理由是同位角相等,两直线平行;
20.
【答案】
99?
【解答】
解:
如图(1),作EHDF,由折叠得:∠B'EF=∠FEM=27e
∠B'EM=∠BEF+∠FEM=27?+27?=54?
AE//DF
∠EFM=∠B'EF=27?,∠DME=∠BMM=54?
∠BMF=∠DME=54?
BM//CF
∠CFM+∠BMF=180?
∠CFM=180?-54?=126?
图③
由折叠得:
如图③,∠MFC=126?
∴ ∠EFC=∠MFC-∠EFM=126?-27?=99?
故填:99?
三、 解答题 (本题共计 6 小题 ,每题 10 分 ,共计60分 )
21.
【答案】
解:(1)如图所示,
DE即为所求作的平行线.
(2)∵ DE//BC,
∴ ∠ADE=∠B=50?(两直线平行,同位角相等).
【解答】
解:(1)如图所示,
DE即为所求作的平行线.
(2)∵ DE//BC,
∴ ∠ADE=∠B=50?(两直线平行,同位角相等).
22.
【答案】
AEIlBF,理由见解析.
【解答】
解:AE//BF.理由如下:
.AC⊥AB,BD⊥AB.
∠BAC=∠DBA=90?,
∵ ∠CAE=∠DEF,
.∠BAE=FBA
FB//AE
23.
【答案】
解:(1)如图,垂线CD即为所求;
(2)如图,直线AE即为所求;
(3)三条边中,AB最长,
∵ ∠C=90?,
∴ AC⊥CB,AC,BC都为垂线段,
∴ AB>AC,AB>BC,即三条边中,AB最长.
【解答】
解:(1)如图,垂线CD即为所求;
(2)如图,直线AE即为所求;
(3)三条边中,AB最长,
∵ ∠C=90?,
∴ AC⊥CB,AC,BC都为垂线段,
∴ AB>AC,AB>BC,即三条边中,AB最长.
24.
【答案】
证明:∵ CB=CE,
∴ ∠B=∠CEB,
又∵ ∠A=∠B,
∴ ∠A=∠CEB,
∴ CE?//?AD.
【解答】
证明:∵ CB=CE,
∴ ∠B=∠CEB,
又∵ ∠A=∠B,
∴ ∠A=∠CEB,
∴ CE?//?AD.
25.
【答案】
解:(1)如图所示:
(2)在三角形AOC中有∠A=50?,∠OCA=90?,?
∴ ∠AOC=40?,?
又∠AOB=90?,?
∴ ∠COB=50?.
(3)如图所示;
当OC1∥AB时,此时OC旋转了90度,90÷10=9(秒) ;
当OC2∥AB时,此时OC旋转了270度,此时270÷10=27(秒),
故答案为:9或27.
【解答】
解:(1)如图所示:
(2)在三角形AOC中有∠A=50?,∠OCA=90?,
∴ ∠AOC=40?,
又∠AOB=90?,
∴ ∠COB=50?.
(3)如图所示;
当OC1∥AB时,此时OC旋转了90度,90÷10=9(秒) ;
当OC2∥AB时,此时OC旋转了270度,此时270÷10=27(秒),
故答案为:9或27.
26.
【答案】
180?
证明:在四边形OECF中
由∠C=90?,a⊥b,
得∠OEC+∠OFC=180?,
因为∠MEC=180?-∠OEC,
∠NFC=180?-∠OFC,
所以∠MEC+∠NFC=(180?-∠OEC)+(180?-∠OFC)
=360?-(∠OEC+∠OFC)
=360?-180?=180?,
因EG,FH分别平分∠MEC和∠NFC,
所以∠CEG=12∠MEC,∠CFH=12∠NFC,
所以∠CEG+∠CFH=12(∠MEC+∠NFC)=12×180?=90?,
过C点作CD?//?EG,
所以∠CEG=∠DCE,
因为∠DCE+∠DCF=90?,
∠CEG+∠CFH=90?,
所以∠DCF=∠CFH,
所以CD?//?FH,
又因为CD?//?EG,
所EG?//?FH.
【解答】
在四边形OECF中
由∠C=90?,a⊥b,
得∠OEC+∠OFC=180?,
故答案为:180?;
证明:在四边形OECF中
由∠C=90?,a⊥b,
得∠OEC+∠OFC=180?,
因为∠MEC=180?-∠OEC,
∠NFC=180?-∠OFC,
所以∠MEC+∠NFC=(180?-∠OEC)+(180?-∠OFC)
=360?-(∠OEC+∠OFC)
=360?-180?=180?,
因EG,FH分别平分∠MEC和∠NFC,
所以∠CEG=12∠MEC,∠CFH=12∠NFC,
所以∠CEG+∠CFH=12(∠MEC+∠NFC)=12×180?=90?,
过C点作CD?//?EG,
所以∠CEG=∠DCE,
因为∠DCE+∠DCF=90?,
∠CEG+∠CFH=90?,
所以∠DCF=∠CFH,
所以CD?//?FH,
又因为CD?//?EG,
所EG?//?FH.
班级:_____________姓名:_____________
一、 选择题 (本题共计 10 小题 ,每题 3 分 ,共计30分 , ) ?
1. 在同一平面内,两直线可能的位置关系是( )
A.相交 B.平行
C.相交或平行 D.相交、平行或垂直?
2. 同一平面内有三条直线,如果其中只有两条平行,那么它们( )
A.没有交点 B.有一个交点 C.有两个交点 D.有三个交点?
3. 下列说法不正确的是( )
A.过马路的斑马线是平行线
B.100米跑道的跑道线是平行线
C.若a?//?b,b?//?d,则a⊥d
D.过直线外一点有且只有一条直线与已知直线平行?
4. 在同一平面内,两条直线的位置关系是( )
A.平行或垂直 B.平行或相交
C.垂直或相交 D.平行、垂直或相交?
5. 如图,点E在BC的延长线上,下列条件中不能判定AB?//?CD的是(? ? ? ? )
?
A.∠3=∠4 B.∠1=∠2
C.∠B=∠DCE D.∠D+∠DAB=180?
?6. 如图,下列四组条件中,能说明AB?//?CD的是(? ? ? ? )
A.∠1=∠2 B.∠BAD=∠BCD
C.∠ABC=∠ADC,∠3=∠4 D.∠BAD+∠ABC=180?
7. 已知同一平面内的三条直线a,b,c,下列命题中错误的是( )
A.∵ a?//?b,b?//?c,∴ a?//?c B.∵ a⊥b,b⊥c,∴ a?//?c
C.∵ a?//?b,b⊥c,∴ a⊥c D.∵ a⊥b,b⊥c,∴ a⊥c?
8. 下列说法正确的是(? ? ? ? )
①在同一平面内,不相交的两条直线叫做平行线;
②在同一平面内,过一点有且仅有一条直线与已知直线平行;
③平面内,过一点有且仅有一条直线与已知直线垂直;
④平行于同一条直线的两条直线平行;
A.①② B.①③ C.①②③ D.①③④?
9. 下列结论正确的是( )
A.不相交的两条直线叫做平行线
B.两条直线被第三条直线所截,同位角相等
C.垂直于同一直线的两条直线互相平行
D.平行于同一直线的两条直线互相平行?
10. 下列说法中,正确的个数为( )
(1)过一点有无数条直线与已知直线平行
(2)如果a?//?b,a?//?c,那么b?//?c
(3)如果两线段不相交,那么它们就平行
(4)如果两直线不相交,那么它们就平行
A.1个 B.2个 C.3个 D.4个
二、 填空题 (本题共计 10 小题 ,每题 3 分 ,共计30分 , ) ?
11. 若AB?//?CD,AB?//?EF,则________. ?
12. 在同一平面内的三条直线,其中有两条直线平行,则这第三条直线的交点一定有两个________.
?
13. 如图,在正方体中,与线段AB平行的线段有________. ?
14. 如图,现给出下列条件:①∠1=∠2,②∠B=∠5,③∠3=∠4,④∠5=∠D,⑤∠B+∠BCD=180?,其中能够得到AB//CD的条件是________(填序号);能够得到AD//BC的条件是________.(填序号)
?
15. 如图,共有________组平行线段. ?
16. 如图所示,请写出能判定CE//AB的一个条件________.
?17. 如果两条直线都与第三条直线平行,那么这两条直线________.也叫做平行线的传递性. ?
18. 下列说法中:
(1)不相交的两条直线叫做平行线; (2)经过一点,有且只有一条直线与已知直线平行;
(3)垂直于同一条直线的两直线平行; (4)直线a?//?b,b?//?c,则a?//?c;
(5)两条直线被第三条直线所截,同位角相等.其中正确的是________.
?19. 如图,用直尺和三角尺作出直线AB、CD,得到AB?//?CD的理由是________.
?
20. 如图,图①是一个四边形纸条,其中,分别为边上的两点,且,将纸条沿所在的直线折叠得到图②,再将图②中的四边形沿所在直线折叠得到图③,则图③中的度数为________
三、 解答题 (本题共计 6 小题 ,共计60分 , )
21. 如图,在△ABC中,AB>AC,点D在边上.
(1)过点D,作平行线DE//BC,交AC于点E.(尺规作图,不写作法,保留作图痕迹)
(2)在上(1)中,若∠B=50?,∠A=60?,求∠ADE的度数.
?
22. 已知:如图,请猜想直线AE与BF的位置关系,并说明理由.
?
23. 如图,三角形ABC中, ∠C=90? .根据语句画图,并回答问题.
(1)过点C画AB的垂线,交AB于点D;
(2)过点A画AE//CB;
(3)三条边AB,AC,BC中哪条边最长?为什么?
?
24. 如图,在四边形ABCD中,∠A=∠B,CB=CE.求证:CE?//?AD.
?
25. 已知:如图,在△AOB中∠O=90?,∠A=50?.
(1)根据下列语句画图:过点O作OC⊥AB,垂足为C,过点C作CD∥OA交OB于点D;
(2)求(1)中作出图中的∠COB的度数;
(3)将(1)中作出图中的△COD绕点O按每秒10?的速度沿顺时针方向旋转一周,当旋转________秒时(直接写结果边OC恰好与边AB平行.
?26. 如图,直线a⊥b,垂足为O,△ABC与直线a、b分别交于点E、F,且∠C=90?,EG、FH分别平分∠MEC和∠NFC.
(1)填空:∠OEC+∠OFC=________;
(2)求证:EG?//?FH.
参考答案
一、 选择题 (本题共计 10 小题 ,每题 3 分 ,共计30分 )
1.
【答案】
C
【解答】
解:平面内,两直线的位置关系是相交或平行(其中,垂直是相交的特例).
故选C.
2.
【答案】
C
【解答】
解:根据题意,第三条直线与这两条平行直线各有一个交点.
故选:C.
3.
【答案】
C
【解答】
解:A,B,由平行线的定义可知,斑马线是平行线,100米跑道的跑道线是平行线,A,B正确;
C,根据平行于同一条直线的两直线平行可知,C错误;
D,过直线外一点有且只有一条直线与已知直线平行,这是平行公理,D正确.
故选C.
4.
【答案】
B
【解答】
解:在同一个平面内,两条直线只有两种位置关系,即平行或相交,
故选:B.
5.
【答案】
A
【解答】
解:A,∠3与∠4是直线AD,BC被AC所截形成的内错角,因为∠3=∠4,所以应是AD?//?BC,故A符合题意;
B,∵ ∠1=∠2,∴ AB?//?CD?(内错角相等,两直线平行),故B不符合题意;
C,∵ ∠DCE=∠B,∴ AB?//?CD?(同位角相等,两直线平行),故C不符合题意;
D,∵ ∠D+∠DAB=180?,∴ AB?//?CD(同旁内角互补,两直线平行),故D不符合题意.
故选A.
6.
【答案】
C
【解答】
解:A、根据∠1=∠2能推出AD//BC,不能推出AB?//?CD,故本选项不符合题意;
B、根据∠BAD=∠BCD不能推出AB?//?CD,故本选项不符合题意;
C、根据∠ABC=∠ADC,∠3=∠4,则∠ABD=∠CDB,能推出AB?//?CD,故本选项符合题意;
D、根据∠BAD+∠ABC=180?能推出AD//BC,不能推出AB?//?CD,故本选项不符合题意.
故选C.
7.
【答案】
D
【解答】
解:A、如果a?//?b,b?//?c,那么a?//?c,正确;
B、如果a⊥b,b⊥c,那么a?//?c,正确;
C、如果a?//?b,b⊥c,那么a⊥c,正确;
D、如果a⊥b,b⊥c,那么a?//?c,错误.
故选:D.
8.
【答案】
D
【解答】
解:①在同一平面内,不相交的两条直线叫做平行线,正确;
②在同一平面内,过一点有且仅有一条直线与已知直线平行,错误,应该是过直线外一点有且仅有一条直线平行于已知直线;
③平面内,过一点有且仅有一条直线与已知直线垂直,正确;
④平行于同一条直线的两条直线平行,正确.
故选D.
9.
【答案】
D
【解答】
解:A、在同一平面内,不相交的两条直线叫做平行线,故A不符合题意;
B、两直线平行,同位角相等,故B不符合题意;
C、在同一平面内,垂直于同一条直线的两条直线互相平行,故C不符合题意;
D、平行于同一直线的两条直线互相平行,故D符合题意;
故选:D.
10.
【答案】
A
【解答】
解:(1)过直线外一点有且只有一条直线与已知直线平行,故错误;
(2)根据平行公理的推论,正确;
(3)线段的长度是有限的,不相交也不一定平行,故错误;
(4)应该是“在同一平面内”,故错误.
正确的只有一个,故选A.
二、 填空题 (本题共计 10 小题 ,每题 3 分 ,共计30分 )
11.
【答案】
CD?//?EF
【解答】
解:根据平行线的传递性,得CD?//?EF.
故答案为CD?//?EF.
12.
【答案】
×
【解答】
解:∵ 如果第三条直线与这两条直线平行则这三条直线没有交点.
∴ 错误.
13.
【答案】
EF、HG、DC
【解答】
解:与AB平行的线段是:DC、EF;
与CD平行的线段是:HG,
所以与AB线段平行的线段有:EF、HG、DC.
故答案是:EF、HG、DC.
14.
【答案】
②③⑤,①④
【解答】
解:能够得到AB//CD的条件是②③⑤.
②∠B=∠5,同位角相等,两直线平行;
③∠3=∠4,内错角相等,两直线平行;
⑤∠B+∠BCD=180?,同旁内角互补,两直线平行.
能够得到AD//BC的条件是①④.
①∠1=∠2,内错角相等,两直线平行;
④∠5=∠D,内错角相等,两直线平行.
故答案为:②③⑤;①④.
15.
【答案】
9
【解答】
解:图中的平行线段有AD?//?EF;BD?//?EF;DE?//?FB;DE?//?FC;DF?//?AE;DF?//?EC;DE?//?BC;DF?//?AC;EF?//?AB.共有9对.
故答案为:9.
16.
【答案】
∠DCE=∠A(答案不唯一)
【解答】
解:能判定CE?//?AB的一个条件是:
∠DCE=∠A或∠ECB=∠B或∠A+∠ACE=180?.
故答案为:∠DCE=∠A(答案不唯一).
17.
【答案】
互相平行
【解答】
解:如果两条直线都与第三条直线平行,那么这两条直线互相平行,也叫做平行线的传递性.
故答案为:互相平行.
18.
【答案】
解:(1)在同一平面内,不相交的两条直线叫做平行线;故错误;
(2)经过直线外一点,有且只有一条直线与已知直线平行;故错误;
(3)在同一平面内,垂直于同一条直线的两直线平行;故错误;
(4)直线a?//?b,b?//?c,则a?//?c;故正确;
(5)两条平行直线被第三条直线所截,同位角相等,故错误.
其中正确的是(4).
【解答】
解:(1)在同一平面内,不相交的两条直线叫做平行线;故错误;
(2)经过直线外一点,有且只有一条直线与已知直线平行;故错误;
(3)在同一平面内,垂直于同一条直线的两直线平行;故错误;
(4)直线a?//?b,b?//?c,则a?//?c;故正确;
(5)两条平行直线被第三条直线所截,同位角相等,故错误.
其中正确的是(4).
19.
【答案】
同位角相等,两直线平行
【解答】
用直尺和三角尺作出直线AB、CD,得到AB?//?CD的理由是同位角相等,两直线平行;
20.
【答案】
99?
【解答】
解:
如图(1),作EHDF,由折叠得:∠B'EF=∠FEM=27e
∠B'EM=∠BEF+∠FEM=27?+27?=54?
AE//DF
∠EFM=∠B'EF=27?,∠DME=∠BMM=54?
∠BMF=∠DME=54?
BM//CF
∠CFM+∠BMF=180?
∠CFM=180?-54?=126?
图③
由折叠得:
如图③,∠MFC=126?
∴ ∠EFC=∠MFC-∠EFM=126?-27?=99?
故填:99?
三、 解答题 (本题共计 6 小题 ,每题 10 分 ,共计60分 )
21.
【答案】
解:(1)如图所示,
DE即为所求作的平行线.
(2)∵ DE//BC,
∴ ∠ADE=∠B=50?(两直线平行,同位角相等).
【解答】
解:(1)如图所示,
DE即为所求作的平行线.
(2)∵ DE//BC,
∴ ∠ADE=∠B=50?(两直线平行,同位角相等).
22.
【答案】
AEIlBF,理由见解析.
【解答】
解:AE//BF.理由如下:
.AC⊥AB,BD⊥AB.
∠BAC=∠DBA=90?,
∵ ∠CAE=∠DEF,
.∠BAE=FBA
FB//AE
23.
【答案】
解:(1)如图,垂线CD即为所求;
(2)如图,直线AE即为所求;
(3)三条边中,AB最长,
∵ ∠C=90?,
∴ AC⊥CB,AC,BC都为垂线段,
∴ AB>AC,AB>BC,即三条边中,AB最长.
【解答】
解:(1)如图,垂线CD即为所求;
(2)如图,直线AE即为所求;
(3)三条边中,AB最长,
∵ ∠C=90?,
∴ AC⊥CB,AC,BC都为垂线段,
∴ AB>AC,AB>BC,即三条边中,AB最长.
24.
【答案】
证明:∵ CB=CE,
∴ ∠B=∠CEB,
又∵ ∠A=∠B,
∴ ∠A=∠CEB,
∴ CE?//?AD.
【解答】
证明:∵ CB=CE,
∴ ∠B=∠CEB,
又∵ ∠A=∠B,
∴ ∠A=∠CEB,
∴ CE?//?AD.
25.
【答案】
解:(1)如图所示:
(2)在三角形AOC中有∠A=50?,∠OCA=90?,?
∴ ∠AOC=40?,?
又∠AOB=90?,?
∴ ∠COB=50?.
(3)如图所示;
当OC1∥AB时,此时OC旋转了90度,90÷10=9(秒) ;
当OC2∥AB时,此时OC旋转了270度,此时270÷10=27(秒),
故答案为:9或27.
【解答】
解:(1)如图所示:
(2)在三角形AOC中有∠A=50?,∠OCA=90?,
∴ ∠AOC=40?,
又∠AOB=90?,
∴ ∠COB=50?.
(3)如图所示;
当OC1∥AB时,此时OC旋转了90度,90÷10=9(秒) ;
当OC2∥AB时,此时OC旋转了270度,此时270÷10=27(秒),
故答案为:9或27.
26.
【答案】
180?
证明:在四边形OECF中
由∠C=90?,a⊥b,
得∠OEC+∠OFC=180?,
因为∠MEC=180?-∠OEC,
∠NFC=180?-∠OFC,
所以∠MEC+∠NFC=(180?-∠OEC)+(180?-∠OFC)
=360?-(∠OEC+∠OFC)
=360?-180?=180?,
因EG,FH分别平分∠MEC和∠NFC,
所以∠CEG=12∠MEC,∠CFH=12∠NFC,
所以∠CEG+∠CFH=12(∠MEC+∠NFC)=12×180?=90?,
过C点作CD?//?EG,
所以∠CEG=∠DCE,
因为∠DCE+∠DCF=90?,
∠CEG+∠CFH=90?,
所以∠DCF=∠CFH,
所以CD?//?FH,
又因为CD?//?EG,
所EG?//?FH.
【解答】
在四边形OECF中
由∠C=90?,a⊥b,
得∠OEC+∠OFC=180?,
故答案为:180?;
证明:在四边形OECF中
由∠C=90?,a⊥b,
得∠OEC+∠OFC=180?,
因为∠MEC=180?-∠OEC,
∠NFC=180?-∠OFC,
所以∠MEC+∠NFC=(180?-∠OEC)+(180?-∠OFC)
=360?-(∠OEC+∠OFC)
=360?-180?=180?,
因EG,FH分别平分∠MEC和∠NFC,
所以∠CEG=12∠MEC,∠CFH=12∠NFC,
所以∠CEG+∠CFH=12(∠MEC+∠NFC)=12×180?=90?,
过C点作CD?//?EG,
所以∠CEG=∠DCE,
因为∠DCE+∠DCF=90?,
∠CEG+∠CFH=90?,
所以∠DCF=∠CFH,
所以CD?//?FH,
又因为CD?//?EG,
所EG?//?FH.
