华师大版八年级上 旋转的特征课件
图片预览








文档简介
(共23张PPT)
图形的运动
1.图形的平移
2.图形的翻折
轴对称图形
钟摆
(1)上面情景中的转动现象,有什么共同的特征?
(2)钟表的指针、秋千在转动过程中,其形状、大小、位置是否发生变化呢?
在平面内,将一个图形绕一个顶点沿某个方向转动一个角度,这样的图形运动称为旋转(cricumrotate),这个定点成为旋转中心,转动的角称为旋转角。旋转不改变图形的大小和形状。
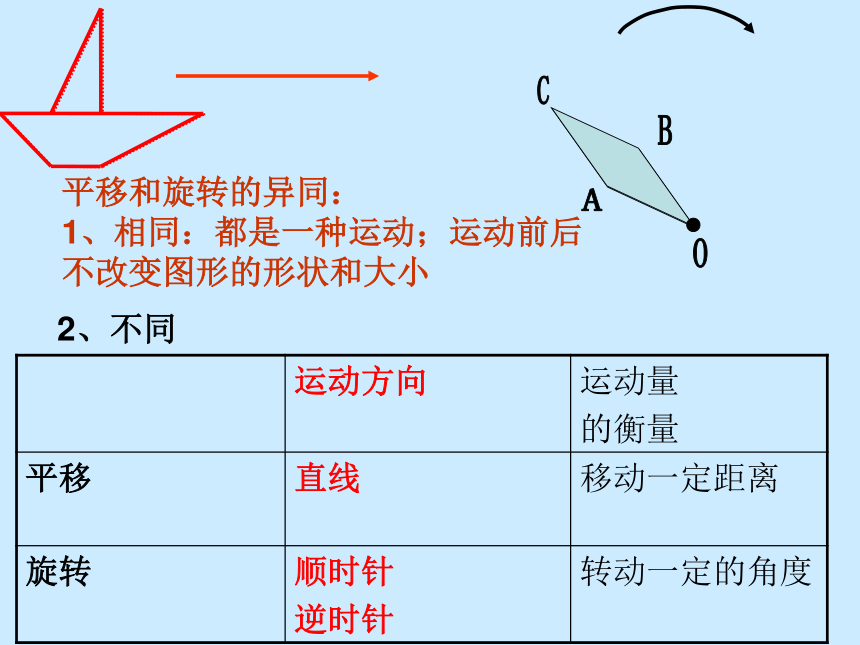
平移和旋转的异同:
1、相同:都是一种运动;运动前后 不改变图形的形状和大小
2、不同
运动方向 运动量
的衡量
平移 直线 移动一定距离
旋转 顺时针
逆时针 转动一定的角度
议一议:
如图所示,如果把钟表的指针看作四边形AOBC,它绕O点按顺时针方向旋转得到四边形DOEF.在这个旋转过程中:
1.旋转中心是什
么?旋转角是什么?
2.经过旋转,点A,B
分别移动到什么位置?
3.AO与DO的长有什么关
系?BO与EO呢?
4.角AOD与角BOE有什
么大小关系?
旋转的基本性质
(1)旋转不改变图形的大小和形状.
(2)图形上的每一点都绕旋转中心沿
相同方向转动了相同的角度.
(3)任意一对对应点与旋转中心的连
线所成的角度都是旋转角.
(4)对应点到旋转中心的距离相等.
例1:钟表的分针匀速旋转一周需要60分.
(1)指出它的旋转中心;
(2)经过20分,分针旋转了多少度?
解:
(1)它的旋转中心是钟表
的轴心;
(2)分针匀速旋转一周需要60
分,因此旋转20分,分针
旋转的角度为
例1:△ABC是等边三角形, △ABP顺时针旋转后能与△CBP’重合,那么(相当于书上的例1)
(1)旋转中心是哪一点?
(2)旋转角是几度?
(3)连结PP’后,△BPP’是什么三角形?
解 (1)旋转中心是点B。
(2) 旋转角等于60°。
(3)∵BP′=BP,
∠ PBP′=∠ABC= 60°,
∴ △BPP’是等边三角形(有一个角
等于60°的等腰三角形是等边三角形)。
巩固练习:1。四边形ABCD是正方形,△DCE顺时针旋转后与△DAF重合,那么
(1)旋转中心是哪一点?
(2)旋转角是几度?
(3)连结EF后,△DEF是什么三角形?
探究:如果等边△ABD旋转后与等边△BCD重合,那么在图形所在的平面内可作为旋转中心的点有几个?
A
B
C
D
图形的旋转
欣赏
旋转
旋转
旋转
旋转
旋转
试一试:某个学生为学校设计了一个直角三角形的绿化带,有一块是正方形草坪和两块直角三角形的花坛组成,现在只知道两个直角三角形的两条斜边长分别为3米和6米,你能求出花坛的面积是多少吗?
3米
6米
1、练习册B 习题16.1
2、试设计一个旋转45度后与自身重合的图形。
随堂练习:
本图案可以看做是一个菱形通过几次旋转得到的?每次旋转了多少度?
做一做:
在图中,正方形ABCD与正方形EFGH边长相等,这个图案可以看作是哪个“基本图案”通过旋转得到的.
图形的运动
1.图形的平移
2.图形的翻折
轴对称图形
钟摆
(1)上面情景中的转动现象,有什么共同的特征?
(2)钟表的指针、秋千在转动过程中,其形状、大小、位置是否发生变化呢?
在平面内,将一个图形绕一个顶点沿某个方向转动一个角度,这样的图形运动称为旋转(cricumrotate),这个定点成为旋转中心,转动的角称为旋转角。旋转不改变图形的大小和形状。
平移和旋转的异同:
1、相同:都是一种运动;运动前后 不改变图形的形状和大小
2、不同
运动方向 运动量
的衡量
平移 直线 移动一定距离
旋转 顺时针
逆时针 转动一定的角度
议一议:
如图所示,如果把钟表的指针看作四边形AOBC,它绕O点按顺时针方向旋转得到四边形DOEF.在这个旋转过程中:
1.旋转中心是什
么?旋转角是什么?
2.经过旋转,点A,B
分别移动到什么位置?
3.AO与DO的长有什么关
系?BO与EO呢?
4.角AOD与角BOE有什
么大小关系?
旋转的基本性质
(1)旋转不改变图形的大小和形状.
(2)图形上的每一点都绕旋转中心沿
相同方向转动了相同的角度.
(3)任意一对对应点与旋转中心的连
线所成的角度都是旋转角.
(4)对应点到旋转中心的距离相等.
例1:钟表的分针匀速旋转一周需要60分.
(1)指出它的旋转中心;
(2)经过20分,分针旋转了多少度?
解:
(1)它的旋转中心是钟表
的轴心;
(2)分针匀速旋转一周需要60
分,因此旋转20分,分针
旋转的角度为
例1:△ABC是等边三角形, △ABP顺时针旋转后能与△CBP’重合,那么(相当于书上的例1)
(1)旋转中心是哪一点?
(2)旋转角是几度?
(3)连结PP’后,△BPP’是什么三角形?
解 (1)旋转中心是点B。
(2) 旋转角等于60°。
(3)∵BP′=BP,
∠ PBP′=∠ABC= 60°,
∴ △BPP’是等边三角形(有一个角
等于60°的等腰三角形是等边三角形)。
巩固练习:1。四边形ABCD是正方形,△DCE顺时针旋转后与△DAF重合,那么
(1)旋转中心是哪一点?
(2)旋转角是几度?
(3)连结EF后,△DEF是什么三角形?
探究:如果等边△ABD旋转后与等边△BCD重合,那么在图形所在的平面内可作为旋转中心的点有几个?
A
B
C
D
图形的旋转
欣赏
旋转
旋转
旋转
旋转
旋转
试一试:某个学生为学校设计了一个直角三角形的绿化带,有一块是正方形草坪和两块直角三角形的花坛组成,现在只知道两个直角三角形的两条斜边长分别为3米和6米,你能求出花坛的面积是多少吗?
3米
6米
1、练习册B 习题16.1
2、试设计一个旋转45度后与自身重合的图形。
随堂练习:
本图案可以看做是一个菱形通过几次旋转得到的?每次旋转了多少度?
做一做:
在图中,正方形ABCD与正方形EFGH边长相等,这个图案可以看作是哪个“基本图案”通过旋转得到的.
