沪教版(上海)初中数学八年级第一学期 18.3(2) 反比例函数的 图像与性质 课件(18张)
文档属性
| 名称 | 沪教版(上海)初中数学八年级第一学期 18.3(2) 反比例函数的 图像与性质 课件(18张) |

|
|
| 格式 | ppt | ||
| 文件大小 | 2.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-12-26 00:00:00 | ||
图片预览


文档简介
§18.3(2) 反比例函数的
图像与性质
2、其定义域是什么?
1、什么是反比例函数?
形如_____________________是反比例函数.
不等于零的一切实数
今天学习反比例函数的图像与性质
(即 )
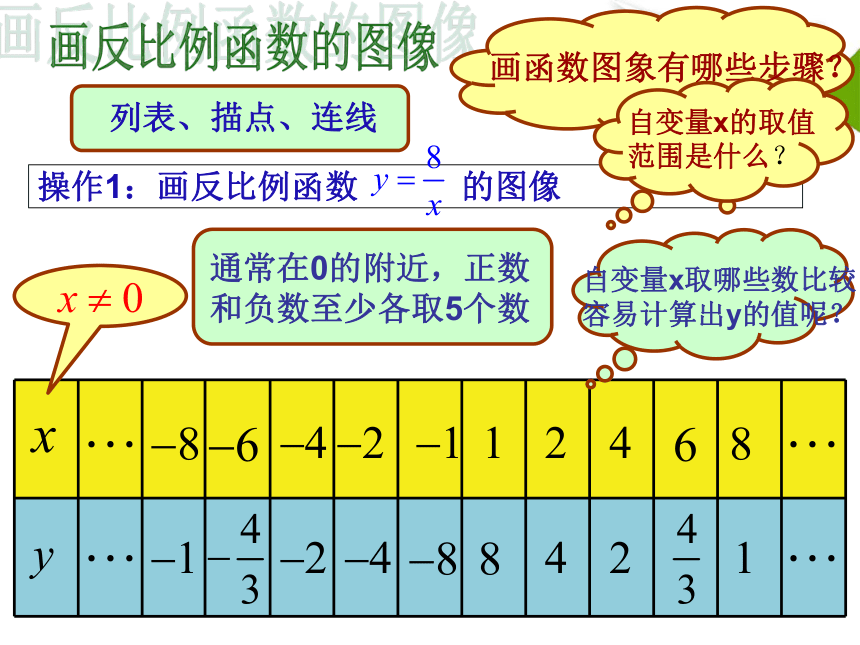
操作1:画反比例函数 的图像
画函数图象有哪些步骤?
列表、描点、连线
自变量x的取值范围是什么?
通常在0的附近,正数和负数至少各取5个数
自变量x取哪些数比较容易计算出y的值呢?
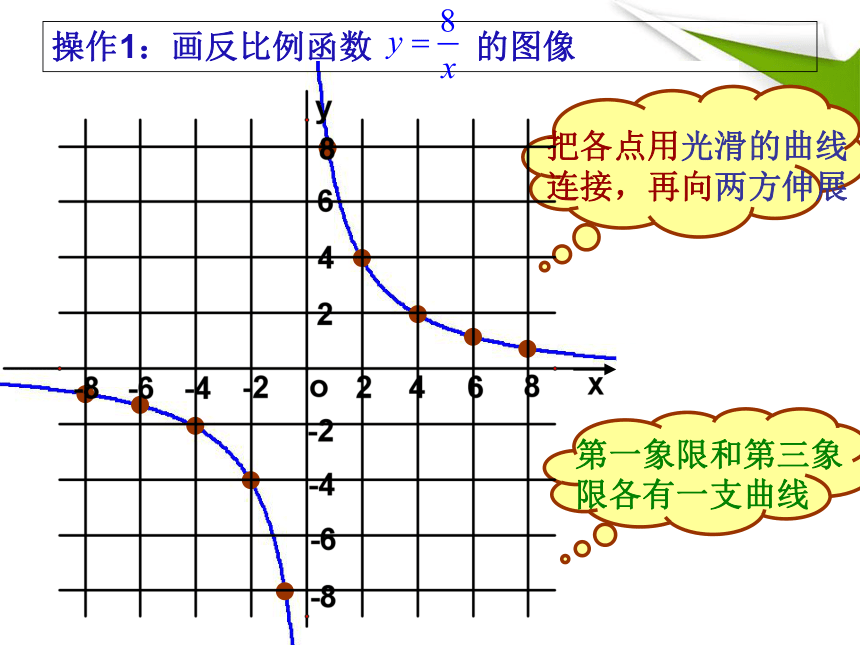
操作1:画反比例函数 的图像
把各点用光滑的曲线连接,再向两方伸展
第一象限和第三象限各有一支曲线
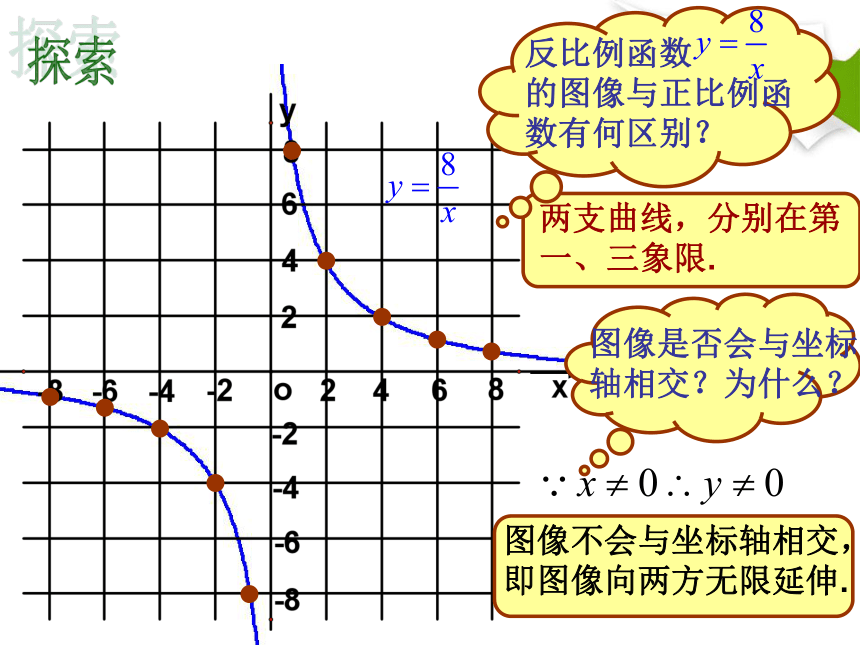
两支曲线,分别在第一、三象限.
反比例函数 的图像与正比例函数有何区别?
图像不会与坐标轴相交,
即图像向两方无限延伸.
图像是否会与坐标轴相交?为什么?
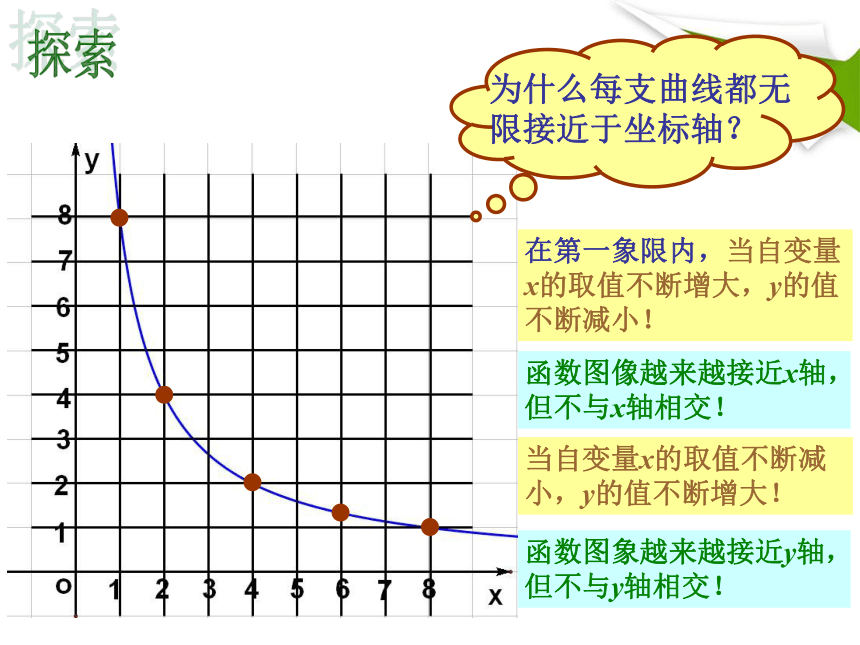
在第一象限内,当自变量x的取值不断增大,y的值不断减小!
当自变量x的取值不断减小,y的值不断增大!
函数图像越来越接近x轴,但不与x轴相交!
函数图象越来越接近y轴,但不与y轴相交!
为什么每支曲线都无限接近于坐标轴?
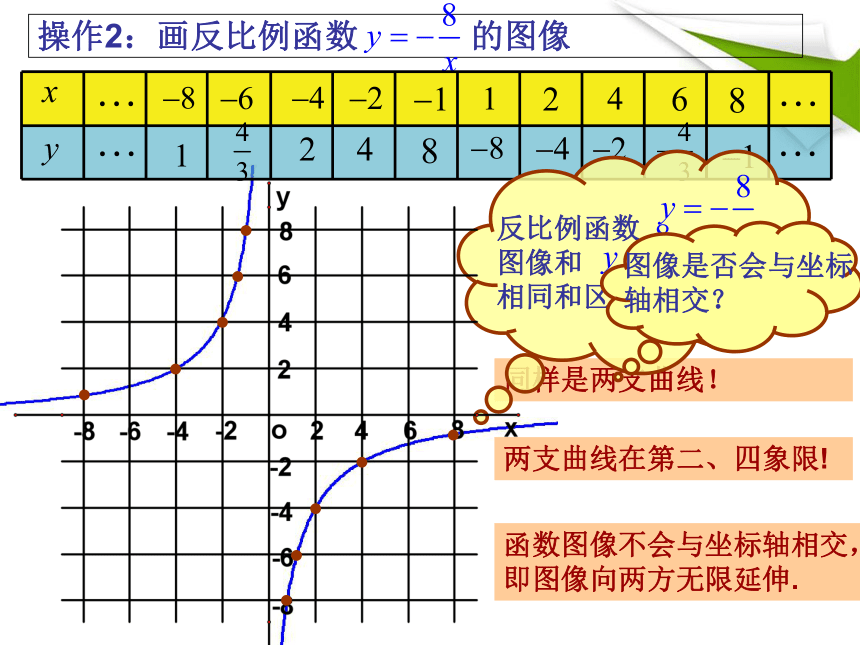
操作2:画反比例函数 的图像
同样是两支曲线!
两支曲线在第二、四象限!
函数图像不会与坐标轴相交,即图像向两方无限延伸.
反比例函数 图像和 有何相同和区别?
图像是否会与坐标轴相交?
反比例函数 的图像叫做双曲线.
双曲线有何特点呢?
双曲线有两支,每支都向两方伸展,无限接近坐标轴,但与坐标轴不相交.
操作3:(1)画反比例函数 和 的图像
操作3:(2)画反比例函数 和 的图像
反比例函数图像所在象限与比例系数k有关
观察!反比例函数图像所在的象限与什么有关?
当k>0时,反比例函数图像在什么位置?
函数图像的两支分别在第一、三象限
观察函数图像上的点,当自变量x的值逐渐增大时,y的值如何变化?
当k>0时,当自变量x的值逐渐增大时,y的值随着逐渐减小.
当x的值从负值变为正值时,y的值突然增大,然后再减小.
因此我们发现,当k>0时,反比例函数的函数值y是“在每个象限内”随x的增大而减小,而不是针对整个定义域.
观察函数图像,当k>0时,y的值是否随着x的增大而一直减小呢?
当k<0时,反比例函数图像在什么位置?
函数图像的两支分别在第二、四象限
观察函数图像上的点,当自变量x的值逐渐增大时,y的值如何变化?
当k<0时,当自变量x的值逐渐增大时,y的值随着逐渐增大.
当x的值从负值变为正值时,y的值突然减小,然后再增大.
因此我们发现,当k<0时,反比例函数的函数值y是“在每个象限内”随x的增大而增大,而不是针对整个定义域.
观察函数图像,当k<0时,y的值是否随着x的增大而一直增大呢?
(1)当k>0时,函数图像的两支分别在第_______象限;在每个象限内,当自变量x的值逐渐增大时,y的值随着逐渐_______;
(2)当k<0时,函数图像的两支分别在第_______象限;在________内,当自变量x的值逐渐_______时,y的值随着逐渐增大.
(3)图像的两支都无限接近于___轴和___轴,但不会与___轴和____轴相交.
一、三
减小
增大
二、四
每个象限
x
y
x
y
在其图像所在的每个象限内,y的值随x的值的增大而
减小的函数是________________.
其中,图像位于第二、四象限的函数是
_________________________________;
1、已知下列反比例函数:
2、如果反比例函数 的图像在第二、四象限,那么正比例函数 的图像经过哪几个象限?
解:
k的符号
图像
位置
性质
通过本节课的学习,你有何收获?
在每个象限内,y的值随x的值增大而减小
在每个象限内,y的值随x的值增大而增大
第一、三象限
第二、四象限
图像两支都无限接近于坐标轴,但不与坐标轴相交
布置作业:练习册,习题18.3(2)
图像与性质
2、其定义域是什么?
1、什么是反比例函数?
形如_____________________是反比例函数.
不等于零的一切实数
今天学习反比例函数的图像与性质
(即 )
操作1:画反比例函数 的图像
画函数图象有哪些步骤?
列表、描点、连线
自变量x的取值范围是什么?
通常在0的附近,正数和负数至少各取5个数
自变量x取哪些数比较容易计算出y的值呢?
操作1:画反比例函数 的图像
把各点用光滑的曲线连接,再向两方伸展
第一象限和第三象限各有一支曲线
两支曲线,分别在第一、三象限.
反比例函数 的图像与正比例函数有何区别?
图像不会与坐标轴相交,
即图像向两方无限延伸.
图像是否会与坐标轴相交?为什么?
在第一象限内,当自变量x的取值不断增大,y的值不断减小!
当自变量x的取值不断减小,y的值不断增大!
函数图像越来越接近x轴,但不与x轴相交!
函数图象越来越接近y轴,但不与y轴相交!
为什么每支曲线都无限接近于坐标轴?
操作2:画反比例函数 的图像
同样是两支曲线!
两支曲线在第二、四象限!
函数图像不会与坐标轴相交,即图像向两方无限延伸.
反比例函数 图像和 有何相同和区别?
图像是否会与坐标轴相交?
反比例函数 的图像叫做双曲线.
双曲线有何特点呢?
双曲线有两支,每支都向两方伸展,无限接近坐标轴,但与坐标轴不相交.
操作3:(1)画反比例函数 和 的图像
操作3:(2)画反比例函数 和 的图像
反比例函数图像所在象限与比例系数k有关
观察!反比例函数图像所在的象限与什么有关?
当k>0时,反比例函数图像在什么位置?
函数图像的两支分别在第一、三象限
观察函数图像上的点,当自变量x的值逐渐增大时,y的值如何变化?
当k>0时,当自变量x的值逐渐增大时,y的值随着逐渐减小.
当x的值从负值变为正值时,y的值突然增大,然后再减小.
因此我们发现,当k>0时,反比例函数的函数值y是“在每个象限内”随x的增大而减小,而不是针对整个定义域.
观察函数图像,当k>0时,y的值是否随着x的增大而一直减小呢?
当k<0时,反比例函数图像在什么位置?
函数图像的两支分别在第二、四象限
观察函数图像上的点,当自变量x的值逐渐增大时,y的值如何变化?
当k<0时,当自变量x的值逐渐增大时,y的值随着逐渐增大.
当x的值从负值变为正值时,y的值突然减小,然后再增大.
因此我们发现,当k<0时,反比例函数的函数值y是“在每个象限内”随x的增大而增大,而不是针对整个定义域.
观察函数图像,当k<0时,y的值是否随着x的增大而一直增大呢?
(1)当k>0时,函数图像的两支分别在第_______象限;在每个象限内,当自变量x的值逐渐增大时,y的值随着逐渐_______;
(2)当k<0时,函数图像的两支分别在第_______象限;在________内,当自变量x的值逐渐_______时,y的值随着逐渐增大.
(3)图像的两支都无限接近于___轴和___轴,但不会与___轴和____轴相交.
一、三
减小
增大
二、四
每个象限
x
y
x
y
在其图像所在的每个象限内,y的值随x的值的增大而
减小的函数是________________.
其中,图像位于第二、四象限的函数是
_________________________________;
1、已知下列反比例函数:
2、如果反比例函数 的图像在第二、四象限,那么正比例函数 的图像经过哪几个象限?
解:
k的符号
图像
位置
性质
通过本节课的学习,你有何收获?
在每个象限内,y的值随x的值增大而减小
在每个象限内,y的值随x的值增大而增大
第一、三象限
第二、四象限
图像两支都无限接近于坐标轴,但不与坐标轴相交
布置作业:练习册,习题18.3(2)
