北师大版初中数学九年级上册期末 总复习-一线三直角模型 教案
文档属性
| 名称 | 北师大版初中数学九年级上册期末 总复习-一线三直角模型 教案 | 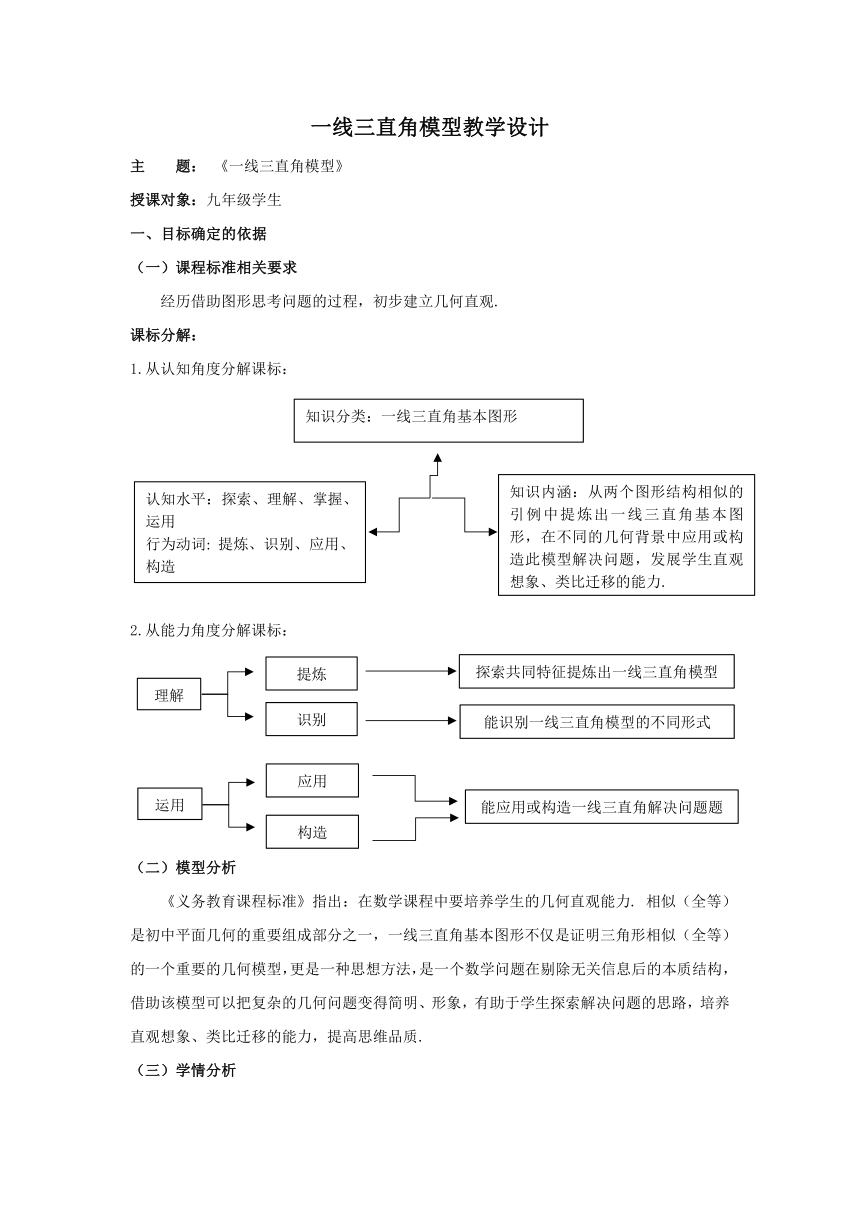 | |
| 格式 | zip | ||
| 文件大小 | 212.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-12-26 10:47:00 | ||
图片预览



文档简介
一线三直角模型教学设计
主
题:
《一线三直角模型》
授课对象:九年级学生
一、目标确定的依据
(一)课程标准相关要求
经历借助图形思考问题的过程,初步建立几何直观.
课标分解:
1.从认知角度分解课标:
2.从能力角度分解课标:
(二)模型分析
《义务教育课程标准》指出:在数学课程中要培养学生的几何直观能力.
相似(全等)是初中平面几何的重要组成部分之一,一线三直角基本图形不仅是证明三角形相似(全等)的一个重要的几何模型,更是一种思想方法,是一个数学问题在剔除无关信息后的本质结构,借助该模型可以把复杂的几何问题变得简明、形象,有助于学生探索解决问题的思路,培养直观想象、类比迁移的能力,提高思维品质.
(三)学情分析
1.
学生的已有基础
知识技能基础:
九年级学生已经能够较熟练的掌握三角形相似和全等的判定方法,具备运用相似(全等)的相关知识解决问题的能力,并且具备了一定的几何说理和有条理的数学表达能力.
活动经验基础:
在七八年级的学习中学生已经经历了观察、归纳、总结、表达等活动过程,经历了几何图形的分析、推理过程,具有一定的作图能力,也积累了一定的合作交流能力.
学生面临的问题
缺乏简洁、明了的几何说理能力;
直观想象、类比迁移的能力和逻辑思维的严谨性有待提高.
(四)核心素养落实分析
数学抽象、逻辑推理、数学建模、数学运算、直观想象、数据分析是培养学生数学学科发展的核心素养.本节课通过探索、归纳、应用等过程主要落实以下核心素养:
(1)通过“识模型”环节,探索两个图形的共同特征,提炼一线三直角模型,培养学生数学抽象的核心素养能力.
(2)通过“用模型”环节,在不同的几何背景中应用或构造一线三直角模型解决问题,发展学生直观想象和逻辑推理的核心素养能力.
依据《课程标准》,根据学生的实际情况及核心素养落实情况,确定本节课的学习目标为:
1.通过探究两个引例,能找到两个图形中的共同特征,提炼并画出一线三直角基本图形;
2.通过以等腰直角三角形为基本工具,能在不同的几何背景中应用或构造一线三直角模型解决问题;
3.通过几何画板演示,能识别一线三直角模型的不同形式.
二、学习重、难点
重点:会应用一线三直角模型解决问题.
难点:一线三直角模型的构造.
评价设计
(一)评价标准
1.能否用规范的语言进行几何说理,依据是否述说准确.
2.能否全面、准确找到两个图形的共同特征,提炼出一线三直角模型,理解一线三直角模型反映的本质问题.
3.能否在不同的几何背景中应用或构造一线三直角模型解决问题.
4.
能否在几何画板演示中,识别一线三直角模型的不同形式.
(二)评价任务
针对目标1:设计了表现式评价,通过对两个引例的探究,复习三角形相似和全等的判定方法,感知图形的共同特征,提炼一线三直角模型.
针对目标2:设计了交流式评价和表现式评价,以等腰直角三角形为基本工具,在不同的背景中应用或构造一线三直角模型解决问题.
针对目标3:设计了表现式评价,通过几何画板演示,识别一线三直角模型的不同形式,由“三直角”变成“三等角”,特殊到一般,引发学生思维发展.
(三)评价样题
实战演练(目标2)
1.(90%)
如图1,点A(5,2)
绕点O逆时针旋转90°到点A',则点A'的坐标为
.
2.(75%)如图2,在矩形ABCD中,AB=4,BC=7,∠BAD的角平分线交BC于点E,EF⊥ED交AB于点F,则EF=
.
图1
图2
四、教法与学法
结合学生已有的知识和活动经验,本节课采用独立思考、探究发现、合作交流的学习方法,创设问题情境,通过观察、联想、类比迁移,鼓励学生先思考,后交流,探索解决问题的方法.
五、教学过程
教学过程共设置五个环节,分别是:识模型、命模型、用模型、悟模型和延模型.
识模型(目标1)
出示两个引例,并由学生上台述说过程.
引例1.
如图,在正方形ABCD中,E为BC上一点(与B、C不重合)
∠AEF=90°,观察图形:
△ABE
与△ECF
有什么关系?并说明理由.
引例2.
如图,在△ABC中,∠BAC=90°,AB=AC,直线MN经过点A,且BF⊥MN于点F,CE⊥MN于点E,观察图形:
△ABF
与△CAE
有什么关系?并说明理由.
【学习评价】关注学生是否能条理清晰的说出证明过程,依据是否表述准确.
思考:
两个图形有什么共同的特征?
能否从两个图形中提炼出一个基本图形?
【学习评价】关注学生对两个图形的共同特征表述是否全面、准确,是否在导学案上正确画出基本图形及班级达成率.
【设计意图】设置两个图形结构相似的引例,便于学生在观察、对比中发现两个图形的共同特征,提炼出基本图形,在证明三角形相似(全等)中总结基本图形中蕴含的知识.
命模型
三个直角顶点在一条直线上
学生根据模型的特征给模型命名:一线三直角
【设计意图】由学生用自己的语言总结图形特征并根据特征给该模型命名,避免教师的灌输,便于学生接受,从而充分调动学生的主观能动性,同时培养了学生的概括表达能力,体现学生的主体地位.
用模型(目标2)
如图,在矩形EFMN中,EF=4,FM=6,当等腰直角三角形ABC的直角顶点C在FM边上移动时,直角边AC始终经过点E,另一直角边BC交MN于点P.
若设FC=x,MP=y,求y与x之间的函数关系式.
变式1.
如图,l1∥l2∥l3,等腰直角三角形ABC的三个顶点分别在l1,l2,l3上,AC=BC=5,相邻两条平行线之间的距离均为h,则h的值为
.
变式2.
如图,在平面直角坐标系中,等腰直角三角形ABC的顶点B在原点处,且点A(2,4),则点C的坐标为
.
【学习评价】关注学生语言表达的规范性.
【设计意图】以等腰直角三角形为基本工具,分别放在矩形、平行线和坐标系三个几何背景中,由可以直接运用一线三直角到构造一线三直角解决问题,由浅入深,层层递进,符合学生认知规律,促进学生思维发展.
悟模型
通过本节课的学习你有哪些收获、感悟和反思.
【设计意图】通过梳理本节课所学知识和方法,培养学生归纳总结的良好习惯.
实战演练(目标2)
1.
如图1,点A(5,2)
绕点O逆时针旋转90°到点A',则点A'的坐标为
.
2.
如图2,在矩形ABCD中,AB=4,BC=7,∠BAD的角平分线交BC于点E,EF⊥ED交AB于点F,则EF=
.
图1
图2
【设计意图】
检测学生本节课的学习效果,第1题易于想到构造一线三直角模型,让学生获得学习的成就感,第2题在识别一线三直角时设置一些干扰,学生需要剔除无关信息找到本质结构.
延模型(目标3)
思考:“三直角”变成“三等角”,△ABF
与△CAE
还全等吗?
【设计意图】通过几何画板演示,让学生观察变中的不变,识别一线三直角的不同形式,对比加深对一线三直角的理解,由“三直角”变成“三等角”,特殊到一般,再次引发学生思考.
课后作业(目标2,3)
如图,在平面直角坐标系中,四边形OABC为矩形,点B的坐标为(1,2),△OAB沿直线OB翻折,点A落在点D处,则点D的坐标为
.
完成“延模型”的思考问题.
【设计意图】课后作业是课堂学习的延伸,第1题类比变式2,再次巩固构造一线三直角解决问题的方法,第2题培养学生由特殊到一般思考问题的数学思想方法.
六、板书设计
主
题:
《一线三直角模型》
授课对象:九年级学生
一、目标确定的依据
(一)课程标准相关要求
经历借助图形思考问题的过程,初步建立几何直观.
课标分解:
1.从认知角度分解课标:
2.从能力角度分解课标:
(二)模型分析
《义务教育课程标准》指出:在数学课程中要培养学生的几何直观能力.
相似(全等)是初中平面几何的重要组成部分之一,一线三直角基本图形不仅是证明三角形相似(全等)的一个重要的几何模型,更是一种思想方法,是一个数学问题在剔除无关信息后的本质结构,借助该模型可以把复杂的几何问题变得简明、形象,有助于学生探索解决问题的思路,培养直观想象、类比迁移的能力,提高思维品质.
(三)学情分析
1.
学生的已有基础
知识技能基础:
九年级学生已经能够较熟练的掌握三角形相似和全等的判定方法,具备运用相似(全等)的相关知识解决问题的能力,并且具备了一定的几何说理和有条理的数学表达能力.
活动经验基础:
在七八年级的学习中学生已经经历了观察、归纳、总结、表达等活动过程,经历了几何图形的分析、推理过程,具有一定的作图能力,也积累了一定的合作交流能力.
学生面临的问题
缺乏简洁、明了的几何说理能力;
直观想象、类比迁移的能力和逻辑思维的严谨性有待提高.
(四)核心素养落实分析
数学抽象、逻辑推理、数学建模、数学运算、直观想象、数据分析是培养学生数学学科发展的核心素养.本节课通过探索、归纳、应用等过程主要落实以下核心素养:
(1)通过“识模型”环节,探索两个图形的共同特征,提炼一线三直角模型,培养学生数学抽象的核心素养能力.
(2)通过“用模型”环节,在不同的几何背景中应用或构造一线三直角模型解决问题,发展学生直观想象和逻辑推理的核心素养能力.
依据《课程标准》,根据学生的实际情况及核心素养落实情况,确定本节课的学习目标为:
1.通过探究两个引例,能找到两个图形中的共同特征,提炼并画出一线三直角基本图形;
2.通过以等腰直角三角形为基本工具,能在不同的几何背景中应用或构造一线三直角模型解决问题;
3.通过几何画板演示,能识别一线三直角模型的不同形式.
二、学习重、难点
重点:会应用一线三直角模型解决问题.
难点:一线三直角模型的构造.
评价设计
(一)评价标准
1.能否用规范的语言进行几何说理,依据是否述说准确.
2.能否全面、准确找到两个图形的共同特征,提炼出一线三直角模型,理解一线三直角模型反映的本质问题.
3.能否在不同的几何背景中应用或构造一线三直角模型解决问题.
4.
能否在几何画板演示中,识别一线三直角模型的不同形式.
(二)评价任务
针对目标1:设计了表现式评价,通过对两个引例的探究,复习三角形相似和全等的判定方法,感知图形的共同特征,提炼一线三直角模型.
针对目标2:设计了交流式评价和表现式评价,以等腰直角三角形为基本工具,在不同的背景中应用或构造一线三直角模型解决问题.
针对目标3:设计了表现式评价,通过几何画板演示,识别一线三直角模型的不同形式,由“三直角”变成“三等角”,特殊到一般,引发学生思维发展.
(三)评价样题
实战演练(目标2)
1.(90%)
如图1,点A(5,2)
绕点O逆时针旋转90°到点A',则点A'的坐标为
.
2.(75%)如图2,在矩形ABCD中,AB=4,BC=7,∠BAD的角平分线交BC于点E,EF⊥ED交AB于点F,则EF=
.
图1
图2
四、教法与学法
结合学生已有的知识和活动经验,本节课采用独立思考、探究发现、合作交流的学习方法,创设问题情境,通过观察、联想、类比迁移,鼓励学生先思考,后交流,探索解决问题的方法.
五、教学过程
教学过程共设置五个环节,分别是:识模型、命模型、用模型、悟模型和延模型.
识模型(目标1)
出示两个引例,并由学生上台述说过程.
引例1.
如图,在正方形ABCD中,E为BC上一点(与B、C不重合)
∠AEF=90°,观察图形:
△ABE
与△ECF
有什么关系?并说明理由.
引例2.
如图,在△ABC中,∠BAC=90°,AB=AC,直线MN经过点A,且BF⊥MN于点F,CE⊥MN于点E,观察图形:
△ABF
与△CAE
有什么关系?并说明理由.
【学习评价】关注学生是否能条理清晰的说出证明过程,依据是否表述准确.
思考:
两个图形有什么共同的特征?
能否从两个图形中提炼出一个基本图形?
【学习评价】关注学生对两个图形的共同特征表述是否全面、准确,是否在导学案上正确画出基本图形及班级达成率.
【设计意图】设置两个图形结构相似的引例,便于学生在观察、对比中发现两个图形的共同特征,提炼出基本图形,在证明三角形相似(全等)中总结基本图形中蕴含的知识.
命模型
三个直角顶点在一条直线上
学生根据模型的特征给模型命名:一线三直角
【设计意图】由学生用自己的语言总结图形特征并根据特征给该模型命名,避免教师的灌输,便于学生接受,从而充分调动学生的主观能动性,同时培养了学生的概括表达能力,体现学生的主体地位.
用模型(目标2)
如图,在矩形EFMN中,EF=4,FM=6,当等腰直角三角形ABC的直角顶点C在FM边上移动时,直角边AC始终经过点E,另一直角边BC交MN于点P.
若设FC=x,MP=y,求y与x之间的函数关系式.
变式1.
如图,l1∥l2∥l3,等腰直角三角形ABC的三个顶点分别在l1,l2,l3上,AC=BC=5,相邻两条平行线之间的距离均为h,则h的值为
.
变式2.
如图,在平面直角坐标系中,等腰直角三角形ABC的顶点B在原点处,且点A(2,4),则点C的坐标为
.
【学习评价】关注学生语言表达的规范性.
【设计意图】以等腰直角三角形为基本工具,分别放在矩形、平行线和坐标系三个几何背景中,由可以直接运用一线三直角到构造一线三直角解决问题,由浅入深,层层递进,符合学生认知规律,促进学生思维发展.
悟模型
通过本节课的学习你有哪些收获、感悟和反思.
【设计意图】通过梳理本节课所学知识和方法,培养学生归纳总结的良好习惯.
实战演练(目标2)
1.
如图1,点A(5,2)
绕点O逆时针旋转90°到点A',则点A'的坐标为
.
2.
如图2,在矩形ABCD中,AB=4,BC=7,∠BAD的角平分线交BC于点E,EF⊥ED交AB于点F,则EF=
.
图1
图2
【设计意图】
检测学生本节课的学习效果,第1题易于想到构造一线三直角模型,让学生获得学习的成就感,第2题在识别一线三直角时设置一些干扰,学生需要剔除无关信息找到本质结构.
延模型(目标3)
思考:“三直角”变成“三等角”,△ABF
与△CAE
还全等吗?
【设计意图】通过几何画板演示,让学生观察变中的不变,识别一线三直角的不同形式,对比加深对一线三直角的理解,由“三直角”变成“三等角”,特殊到一般,再次引发学生思考.
课后作业(目标2,3)
如图,在平面直角坐标系中,四边形OABC为矩形,点B的坐标为(1,2),△OAB沿直线OB翻折,点A落在点D处,则点D的坐标为
.
完成“延模型”的思考问题.
【设计意图】课后作业是课堂学习的延伸,第1题类比变式2,再次巩固构造一线三直角解决问题的方法,第2题培养学生由特殊到一般思考问题的数学思想方法.
六、板书设计
同课章节目录
