沪教版(上海)初中数学八年级第一学期 18.2(3) 正比例函数的性质 课件(23张)
文档属性
| 名称 | 沪教版(上海)初中数学八年级第一学期 18.2(3) 正比例函数的性质 课件(23张) |

|
|
| 格式 | ppt | ||
| 文件大小 | 763.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-12-26 10:21:28 | ||
图片预览





文档简介
九年义务教育《数学》八年级第一学期 (试用本)
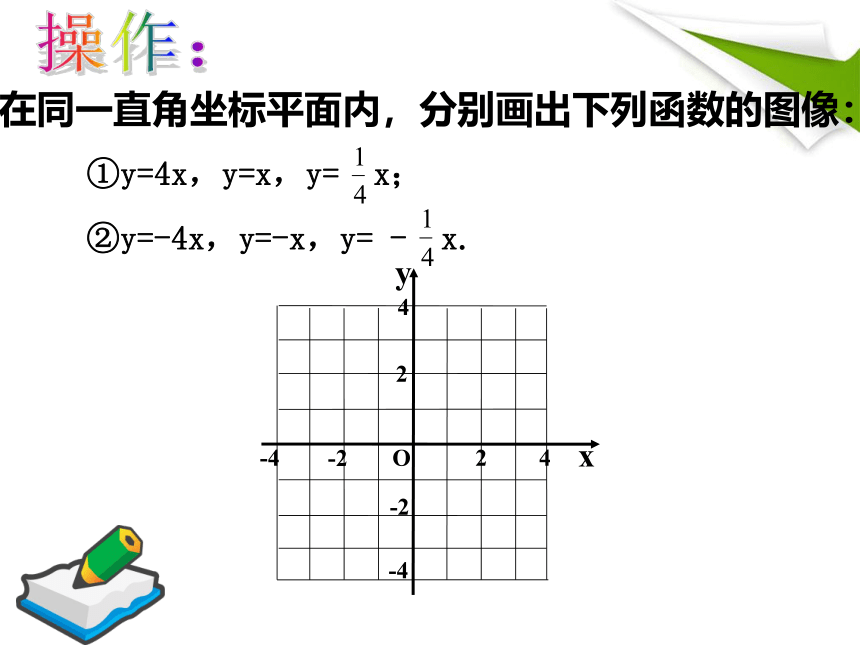
1.解析式形如 y=kx(k是不等于零的常数)的函数叫做正比例函数(其中常数k叫做比例系数).
2.正比例函数y=kx(k≠0)的图象是经过原
点(0,0)和(1,k)的一条直线.
3.①y=4x,y=x,y= x;
②y=-4x,y=-x,y=- x.
在同一直角坐标平面内,分别画出下列函数的图像:
①y=4x,y=x,y= x;
②y=-4x,y=-x,y= - x.
x
y
-4
2
-2
4
-4
2
4
-2
O
观察图像,思考问题.
(1)正比例函数y=kx(k≠0)的图像所经过的两个象限与
常数k有什么关系?
(2)一般来说,对于正比例函数y=kx(k≠0) ,随着自变
量x的值逐渐增大,函数值y将怎样变化?
图中的函数图像经过 两个象限,你认为这时
由 确定的.
(图1)
2
-2
4
-4
2
4
-2
O
y
x
-4
y= x
y=x
y=4x
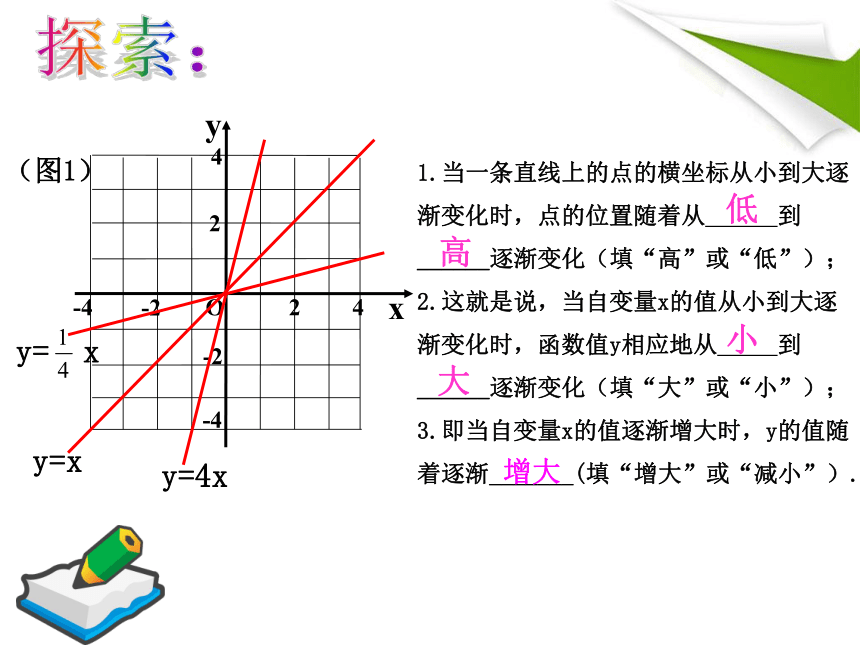
1.当一条直线上的点的横坐标从小到大逐渐变化时,点的位置随着从 到 ______逐渐变化(填“高”或“低”);
2.这就是说,当自变量x的值从小到大逐渐变化时,函数值y相应地从 到
______逐渐变化(填“大”或“小”);
3.即当自变量x的值逐渐增大时,y的值随着逐渐_______(填“增大”或“减小”).
高
低
小
大
增大
2
-2
4
-4
2
4
-2
O
y
x
-4
y=- x
y=-4x
y=-x
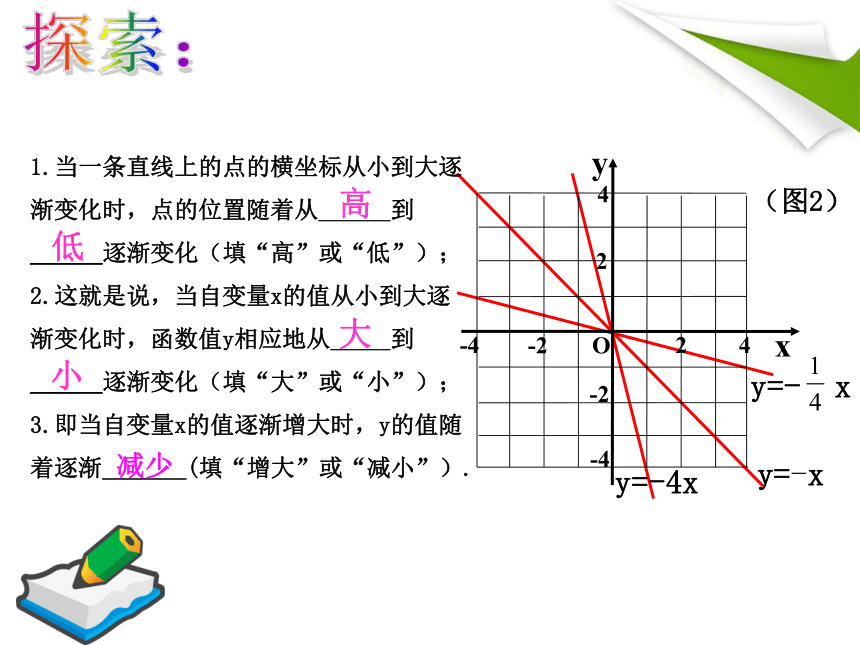
1.当一条直线上的点的横坐标从小到大逐渐变化时,点的位置随着从 到 ______逐渐变化(填“高”或“低”);
2.这就是说,当自变量x的值从小到大逐渐变化时,函数值y相应地从 到
______逐渐变化(填“大”或“小”);
3.即当自变量x的值逐渐增大时,y的值随着逐渐_______(填“增大”或“减小”).
低
高
大
小
(图2)
减少
由画图的操作,通过观察和思考,说说正比例函数有哪些性质?
(1)当k>0时,正比例函数的图像经过第一、三
象限;自变量x的值逐渐增大时,y的值也随
着逐渐增大.
(2)当k<0时,正比例函数的图像经过第二、四
象限;自变量x的值逐渐增大时,y的值也随
着逐渐减小.
正比例函数y= kx (k≠0)的性质:
反之亦成立
1.根据下列正比例函数解析式
来判断其函数图像分布在哪些象限?
一、三象限
一、三象限
二、四象限
请你说出下列函数值的变化情况.
y随x的增大而增大
y随x的增大而增大
y随x的增大而减小
二、四象限
y随x的增大而减小
一、三象限
y随x的增大而增大
B
(2)、 (4)
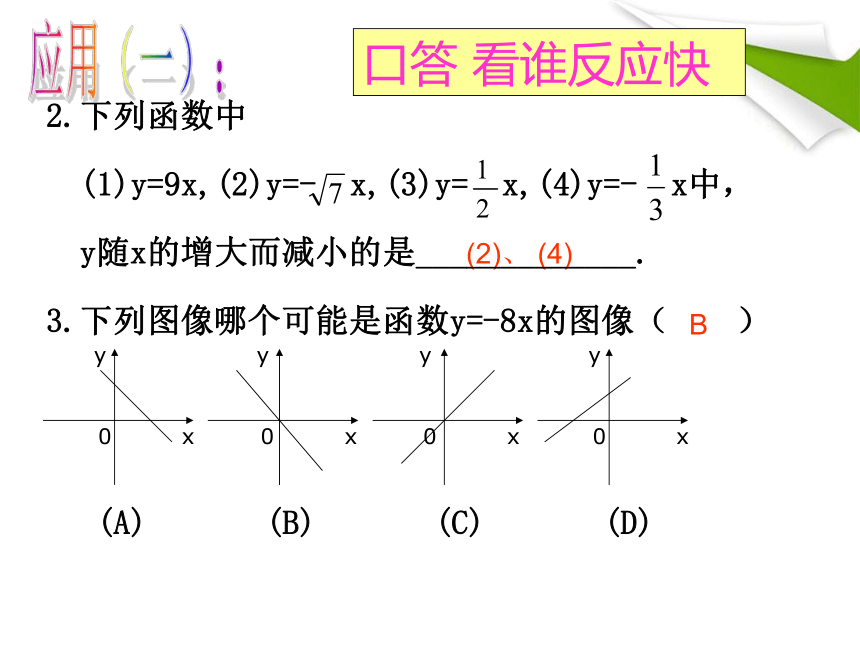
2.下列函数中
(1)y=9x,(2)y=- x,(3)y= x,(4)y=- x中,
y随x的增大而减小的是_____________.
3.下列图像哪个可能是函数y=-8x的图像( )
(A) (B) (C) (D)
x
y
0
x
y
0
x
y
0
x
y
0
口答 看谁反应快
4.某函数具有下面的性质:
(1)它的图象是经过原点的一条直线,
(2)y随x增大反而减小,
请你举出一个满足上述条件的函数,写出解析式.
例题1:已知正比例函数y=(1-2a)x,如果
y的值随x的值增大而减小,
那么a的取值范围是什么?
经过一、三象限,
1-2a<0.
解:由题意得
a> .
a的取值范围是a>
B
正比例函数y=(m-1)x的图象经过一、三象限,
A. m=1
B. m>1
C. m<1
D. m≥1
2.正比例函数y=(3-k)x,如果y随着x的增大而减小,则k的取值范围是________.
k>3
则m的取值范围是( )
3.如果函数 y= - kx 的图像经过二、四象限,那么y = kx 的图像经过第 象限.
二、四
看谁反应快
4.已知 ,则函数 的图像经过第
________象限.
一、三
2
-2
4
-4
2
4
-2
O
y
x
-4
y=- x
y=-4x
y=-x
2
-2
4
-4
2
4
-2
O
y
x
-4
y= x
y=4x
y=x
(图1)
(图2)
观察六个函数图像,它们两两之间位置有什么特殊关系呢?
如果两个正比例函数的图像关于坐标轴对称,那么它们的比例系数有什么关系?
例题2:小明骑自行车从A地到B地,已知骑自行车的速度是每小时6千米,设他骑自行车的路程为y千米、时间为x小时,请写出y与x之间的函数解析式. 若A、 B两地相距12千米,请指出函数的定义域,再画出这个函数的图像.
解:由题意得
函数解析式是y=6x;
函数的定义域是0≤x≤2.
这个函数的图像如图所示:
x(小时)
y(千米)
4
2
6
2
4
O
8
10
12
在解决正比例函数实际应用问题时,应注意什么呢?
在实际问题中,函数的定义域一般是部分实数,所以函数的图像一般就是直线的一部分(还可能只是在一条直线上的一些点).
如果你是正比例函数代言人,你将怎样介绍自己呢?
正 比 例 函 数 的 名 片
嗨:大家好,我是正比例函数,我的变量x与y有很密切的联系,我的解析式是行如…… ,我的图像是……,我的性质有……,
你能否帮我设计一张名片呢?
正 比 例 函 数 的 名 片
解析式
图 像
性 质
k>0
k<0
图像经过一、三象限
y随着x的增大而增大
图像经过二、四象限
y随着x的增大而减少
是经过原点和(1,k)点的一条直线 .
y=kx (k≠0)
已知正比例函数y=(m+1)xm2 ,它的图像
经过第几象限?
解:
比例系数k=m+1=2>0
m=±1,
该函数是正比例函数
m2=1
{
根据正比例函数的性质,k>0可得该图像经过一、三象限。
2.已知:正比例函数
的图像经过第二、四象限,求m的值.
(图2)
观察图像,思考下列问题:
(1)正比例函数y=kx的图像所经过的两个象限与常数k
有什么关系?
(2)一般来说,对于正比例函数y=kx,随着自变量x的
值逐渐增大,函数值y将怎样变化?
函数的图像如图所示.
2
-2
4
-4
2
4
-2
O
y
x
-4
y=- x
y=-4x
y=-x
y=4x
(图1)
2
-2
4
-4
2
4
-2
O
y
x
-4
y= x
y=x
电费y与用电总度数x成正比例.
已知当x=65(度),y=32.5(元).
(2)求当x=26(度)时函数y的值.
(1) 求正比例函数的解析式;
1.解析式形如 y=kx(k是不等于零的常数)的函数叫做正比例函数(其中常数k叫做比例系数).
2.正比例函数y=kx(k≠0)的图象是经过原
点(0,0)和(1,k)的一条直线.
3.①y=4x,y=x,y= x;
②y=-4x,y=-x,y=- x.
在同一直角坐标平面内,分别画出下列函数的图像:
①y=4x,y=x,y= x;
②y=-4x,y=-x,y= - x.
x
y
-4
2
-2
4
-4
2
4
-2
O
观察图像,思考问题.
(1)正比例函数y=kx(k≠0)的图像所经过的两个象限与
常数k有什么关系?
(2)一般来说,对于正比例函数y=kx(k≠0) ,随着自变
量x的值逐渐增大,函数值y将怎样变化?
图中的函数图像经过 两个象限,你认为这时
由 确定的.
(图1)
2
-2
4
-4
2
4
-2
O
y
x
-4
y= x
y=x
y=4x
1.当一条直线上的点的横坐标从小到大逐渐变化时,点的位置随着从 到 ______逐渐变化(填“高”或“低”);
2.这就是说,当自变量x的值从小到大逐渐变化时,函数值y相应地从 到
______逐渐变化(填“大”或“小”);
3.即当自变量x的值逐渐增大时,y的值随着逐渐_______(填“增大”或“减小”).
高
低
小
大
增大
2
-2
4
-4
2
4
-2
O
y
x
-4
y=- x
y=-4x
y=-x
1.当一条直线上的点的横坐标从小到大逐渐变化时,点的位置随着从 到 ______逐渐变化(填“高”或“低”);
2.这就是说,当自变量x的值从小到大逐渐变化时,函数值y相应地从 到
______逐渐变化(填“大”或“小”);
3.即当自变量x的值逐渐增大时,y的值随着逐渐_______(填“增大”或“减小”).
低
高
大
小
(图2)
减少
由画图的操作,通过观察和思考,说说正比例函数有哪些性质?
(1)当k>0时,正比例函数的图像经过第一、三
象限;自变量x的值逐渐增大时,y的值也随
着逐渐增大.
(2)当k<0时,正比例函数的图像经过第二、四
象限;自变量x的值逐渐增大时,y的值也随
着逐渐减小.
正比例函数y= kx (k≠0)的性质:
反之亦成立
1.根据下列正比例函数解析式
来判断其函数图像分布在哪些象限?
一、三象限
一、三象限
二、四象限
请你说出下列函数值的变化情况.
y随x的增大而增大
y随x的增大而增大
y随x的增大而减小
二、四象限
y随x的增大而减小
一、三象限
y随x的增大而增大
B
(2)、 (4)
2.下列函数中
(1)y=9x,(2)y=- x,(3)y= x,(4)y=- x中,
y随x的增大而减小的是_____________.
3.下列图像哪个可能是函数y=-8x的图像( )
(A) (B) (C) (D)
x
y
0
x
y
0
x
y
0
x
y
0
口答 看谁反应快
4.某函数具有下面的性质:
(1)它的图象是经过原点的一条直线,
(2)y随x增大反而减小,
请你举出一个满足上述条件的函数,写出解析式.
例题1:已知正比例函数y=(1-2a)x,如果
y的值随x的值增大而减小,
那么a的取值范围是什么?
经过一、三象限,
1-2a<0.
解:由题意得
a> .
a的取值范围是a>
B
正比例函数y=(m-1)x的图象经过一、三象限,
A. m=1
B. m>1
C. m<1
D. m≥1
2.正比例函数y=(3-k)x,如果y随着x的增大而减小,则k的取值范围是________.
k>3
则m的取值范围是( )
3.如果函数 y= - kx 的图像经过二、四象限,那么y = kx 的图像经过第 象限.
二、四
看谁反应快
4.已知 ,则函数 的图像经过第
________象限.
一、三
2
-2
4
-4
2
4
-2
O
y
x
-4
y=- x
y=-4x
y=-x
2
-2
4
-4
2
4
-2
O
y
x
-4
y= x
y=4x
y=x
(图1)
(图2)
观察六个函数图像,它们两两之间位置有什么特殊关系呢?
如果两个正比例函数的图像关于坐标轴对称,那么它们的比例系数有什么关系?
例题2:小明骑自行车从A地到B地,已知骑自行车的速度是每小时6千米,设他骑自行车的路程为y千米、时间为x小时,请写出y与x之间的函数解析式. 若A、 B两地相距12千米,请指出函数的定义域,再画出这个函数的图像.
解:由题意得
函数解析式是y=6x;
函数的定义域是0≤x≤2.
这个函数的图像如图所示:
x(小时)
y(千米)
4
2
6
2
4
O
8
10
12
在解决正比例函数实际应用问题时,应注意什么呢?
在实际问题中,函数的定义域一般是部分实数,所以函数的图像一般就是直线的一部分(还可能只是在一条直线上的一些点).
如果你是正比例函数代言人,你将怎样介绍自己呢?
正 比 例 函 数 的 名 片
嗨:大家好,我是正比例函数,我的变量x与y有很密切的联系,我的解析式是行如…… ,我的图像是……,我的性质有……,
你能否帮我设计一张名片呢?
正 比 例 函 数 的 名 片
解析式
图 像
性 质
k>0
k<0
图像经过一、三象限
y随着x的增大而增大
图像经过二、四象限
y随着x的增大而减少
是经过原点和(1,k)点的一条直线 .
y=kx (k≠0)
已知正比例函数y=(m+1)xm2 ,它的图像
经过第几象限?
解:
比例系数k=m+1=2>0
m=±1,
该函数是正比例函数
m2=1
{
根据正比例函数的性质,k>0可得该图像经过一、三象限。
2.已知:正比例函数
的图像经过第二、四象限,求m的值.
(图2)
观察图像,思考下列问题:
(1)正比例函数y=kx的图像所经过的两个象限与常数k
有什么关系?
(2)一般来说,对于正比例函数y=kx,随着自变量x的
值逐渐增大,函数值y将怎样变化?
函数的图像如图所示.
2
-2
4
-4
2
4
-2
O
y
x
-4
y=- x
y=-4x
y=-x
y=4x
(图1)
2
-2
4
-4
2
4
-2
O
y
x
-4
y= x
y=x
电费y与用电总度数x成正比例.
已知当x=65(度),y=32.5(元).
(2)求当x=26(度)时函数y的值.
(1) 求正比例函数的解析式;
