沪教版(上海)初中数学八年级第一学期 18.3(2)反比例函数图像和性质课件(18张)
文档属性
| 名称 | 沪教版(上海)初中数学八年级第一学期 18.3(2)反比例函数图像和性质课件(18张) |

|
|
| 格式 | pptx | ||
| 文件大小 | 11.0MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-12-26 10:23:23 | ||
图片预览




文档简介
一、复习引入
(1)学习过哪几类函数?
(2)从哪几方面研究函数?
18.3(2)反比例函数图像和性质
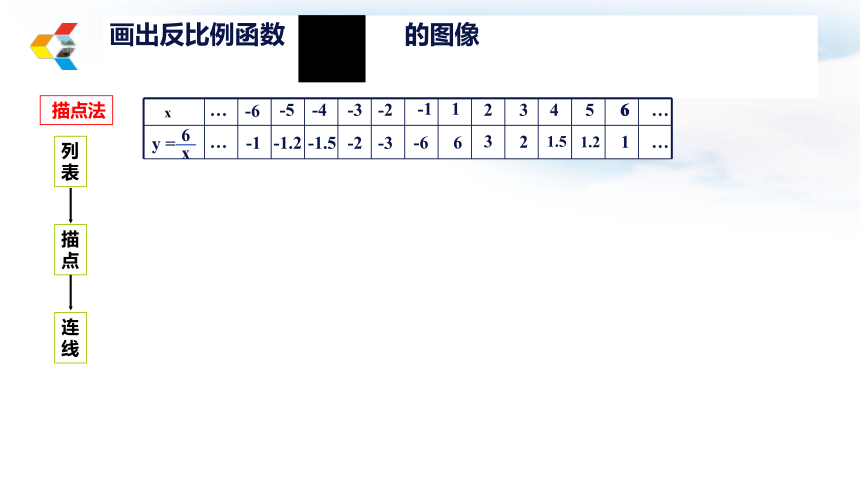
画出反比例函数 的图像
列
表
描
点
连
线
描点法
x
y =
x
6
1
6
2
3
3
2
4
1.5
5
1.2
6
1
6
-1
-6
-2
-3
-3
-1.5
-2
-4
-5
-1.2
-6
-1
…
…
…
…
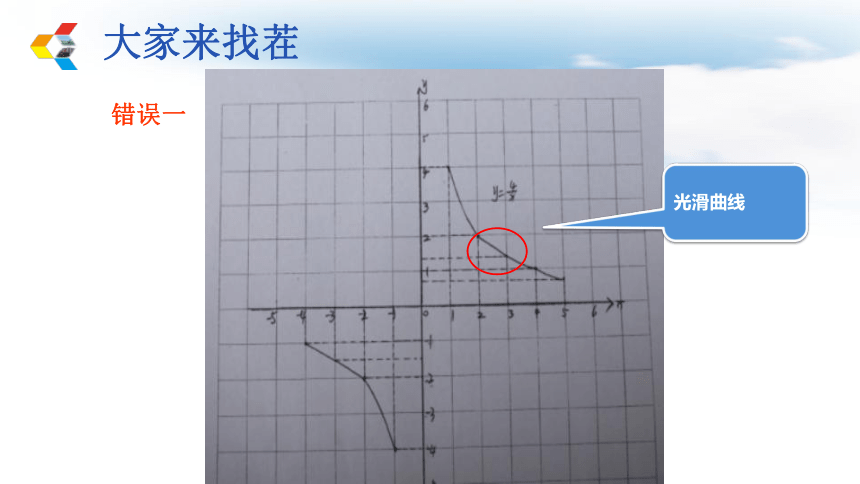
大家来找茬
错误一
光滑曲线
大家来找茬
错误二
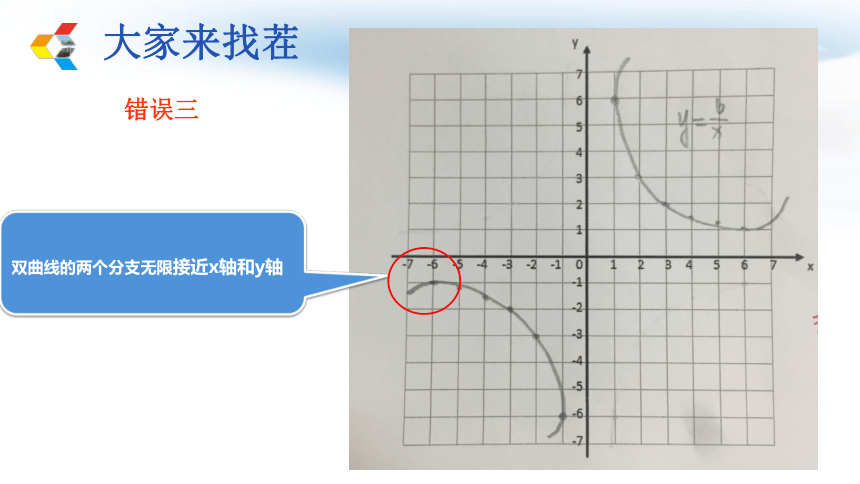
大家来找茬
错误三
双曲线的两个分支无限接近x轴和y轴
能否和 y 轴相交?
能否和 x 轴相交?
画出反比例函数 的图像
列
表
描
点
连
线
描点法
x
y =
x
6
1
6
2
3
3
2
4
1.5
5
1.2
6
1
6
-1
-6
-2
-3
-3
-1.5
-2
-4
-5
-1.2
-6
-1
…
…
…
…
1
2
3
4
5
6
-1
-3
-2
-4
-5
-6
1
2
3
4
-1
-2
-3
-4
0
-6
-5
5
6
x
y =
x
6
y
双曲线的两个分支无限接近x轴和y轴,
但永远不会与x轴和y轴相交
反比例函数 的图像
1
2
3
4
5
6
-1
-3
-2
-4
-5
-6
1
2
3
4
-1
-2
-3
-4
0
-6
-5
5
6
x
y =
x
6
y
注意:① X的值不能为零,左右对称地取值。
② 描点时用光滑曲线顺次连结,切忌用折线。
③ 两个分支
双曲线的两个分支无限接近x轴和y轴,但永远不会与x轴和y轴相交
画出反比例函数 的图像
列
表
描
点
连
线
y
x
y =
x
6
1
2
3
4
5
6
6
-1
-2
-3
-4
-5
-6
…
…
-6
6
3
-3
2
-2
1.5
-1.5
1.2
-1.2
1
-1
…
…
1
2
3
4
5
6
-1
-3
-2
-4
-5
-6
1
2
3
4
-1
-2
-3
-4
0
-6
-5
5
6
x
y =
x
6
1
2
3
4
5
6
-1
-3
-2
-4
-5
-6
1
2
3
4
-1
-2
-3
-4
0
-6
-5
5
6
x
y =
x
6
y
y
1
2
3
4
5
6
-1
-3
-2
-4
-5
-6
1
2
3
4
-1
-2
-3
-4
0
-6
-5
5
6
x
y =
x
6
观察、比较函数 和 的图像, 思考下列问题:
(1) 你能发现他们图像的共同点和不同点吗?
(2)函数图像坐落的象限位置由哪个因素决定?
(3)在每个象限内,y随x 的变化如何变化?
A:
x
y
o
B:
x
y
o
D:
x
y
o
C:
x
y
o
1、反比例函数y= - 的图象大致是( )
D
活学活用
下列函数中 y 随 x 的增大而减小的是 ( )
A、
B、
C、
D、
C
——
在每个象限内
巩固应用
函数 的图像在第 象限,
在每个象限内, y 随着 x 的增大而 .
一、三
减小
2. 函数 的图像在第 象限,
在每个象限内, y 随着 x 的增大而 .
二、四
增大
巩固应用
3. 判断
(1)对于函数 ,在每个象限内,y 随着 x 的增大而增大. ( )
反比例函数,K>0
减小
×
(2)对于函数 ,当x>0时, y 随着 x 的增大而增大. ( )
正比例函数,K>0
√
4.已知 k>0,则函数 , 在同一坐标系中的图象大致是 ( )
x
y
0
x
y
0
x
y
0
x
y
0
(A)
(B)
(C)
(D)
B
5.已知 k<0,则函数 , 在同一坐标系中的图象大致是 ( )
x
y
0
x
y
0
x
y
0
x
y
0
(A)
(B)
(C)
(D)
D
拓展提升
1. 反比例函数 的图像在第 象限,
在每个象限内, y 随着 x 的增大而 .
一、三
减小
2. 反比例函数 的图像在第一、三象限内,
那么K的取值范围是 .
K>3
3. 反比例函数 ,在每个象限内,y随x的增大而增大,
那么K的取值范围是 .
K<2
反比例函数的图象和性质:
图象是双曲线
当k>0时,双曲线分别位于第一,三象限内
当k<0时, 双曲线分别位于第二,四象限内
当k>0时, 在每一象限内 , y随x的增大而减小
当k<0时, 在每一象限内 , y随x的增大而增大
双曲线无限接近于 x、y 轴, 但永远不会与坐标轴相交
形状
位置
增减性
变化趋势
课堂总结
(1)学习过哪几类函数?
(2)从哪几方面研究函数?
18.3(2)反比例函数图像和性质
画出反比例函数 的图像
列
表
描
点
连
线
描点法
x
y =
x
6
1
6
2
3
3
2
4
1.5
5
1.2
6
1
6
-1
-6
-2
-3
-3
-1.5
-2
-4
-5
-1.2
-6
-1
…
…
…
…
大家来找茬
错误一
光滑曲线
大家来找茬
错误二
大家来找茬
错误三
双曲线的两个分支无限接近x轴和y轴
能否和 y 轴相交?
能否和 x 轴相交?
画出反比例函数 的图像
列
表
描
点
连
线
描点法
x
y =
x
6
1
6
2
3
3
2
4
1.5
5
1.2
6
1
6
-1
-6
-2
-3
-3
-1.5
-2
-4
-5
-1.2
-6
-1
…
…
…
…
1
2
3
4
5
6
-1
-3
-2
-4
-5
-6
1
2
3
4
-1
-2
-3
-4
0
-6
-5
5
6
x
y =
x
6
y
双曲线的两个分支无限接近x轴和y轴,
但永远不会与x轴和y轴相交
反比例函数 的图像
1
2
3
4
5
6
-1
-3
-2
-4
-5
-6
1
2
3
4
-1
-2
-3
-4
0
-6
-5
5
6
x
y =
x
6
y
注意:① X的值不能为零,左右对称地取值。
② 描点时用光滑曲线顺次连结,切忌用折线。
③ 两个分支
双曲线的两个分支无限接近x轴和y轴,但永远不会与x轴和y轴相交
画出反比例函数 的图像
列
表
描
点
连
线
y
x
y =
x
6
1
2
3
4
5
6
6
-1
-2
-3
-4
-5
-6
…
…
-6
6
3
-3
2
-2
1.5
-1.5
1.2
-1.2
1
-1
…
…
1
2
3
4
5
6
-1
-3
-2
-4
-5
-6
1
2
3
4
-1
-2
-3
-4
0
-6
-5
5
6
x
y =
x
6
1
2
3
4
5
6
-1
-3
-2
-4
-5
-6
1
2
3
4
-1
-2
-3
-4
0
-6
-5
5
6
x
y =
x
6
y
y
1
2
3
4
5
6
-1
-3
-2
-4
-5
-6
1
2
3
4
-1
-2
-3
-4
0
-6
-5
5
6
x
y =
x
6
观察、比较函数 和 的图像, 思考下列问题:
(1) 你能发现他们图像的共同点和不同点吗?
(2)函数图像坐落的象限位置由哪个因素决定?
(3)在每个象限内,y随x 的变化如何变化?
A:
x
y
o
B:
x
y
o
D:
x
y
o
C:
x
y
o
1、反比例函数y= - 的图象大致是( )
D
活学活用
下列函数中 y 随 x 的增大而减小的是 ( )
A、
B、
C、
D、
C
——
在每个象限内
巩固应用
函数 的图像在第 象限,
在每个象限内, y 随着 x 的增大而 .
一、三
减小
2. 函数 的图像在第 象限,
在每个象限内, y 随着 x 的增大而 .
二、四
增大
巩固应用
3. 判断
(1)对于函数 ,在每个象限内,y 随着 x 的增大而增大. ( )
反比例函数,K>0
减小
×
(2)对于函数 ,当x>0时, y 随着 x 的增大而增大. ( )
正比例函数,K>0
√
4.已知 k>0,则函数 , 在同一坐标系中的图象大致是 ( )
x
y
0
x
y
0
x
y
0
x
y
0
(A)
(B)
(C)
(D)
B
5.已知 k<0,则函数 , 在同一坐标系中的图象大致是 ( )
x
y
0
x
y
0
x
y
0
x
y
0
(A)
(B)
(C)
(D)
D
拓展提升
1. 反比例函数 的图像在第 象限,
在每个象限内, y 随着 x 的增大而 .
一、三
减小
2. 反比例函数 的图像在第一、三象限内,
那么K的取值范围是 .
K>3
3. 反比例函数 ,在每个象限内,y随x的增大而增大,
那么K的取值范围是 .
K<2
反比例函数的图象和性质:
图象是双曲线
当k>0时,双曲线分别位于第一,三象限内
当k<0时, 双曲线分别位于第二,四象限内
当k>0时, 在每一象限内 , y随x的增大而减小
当k<0时, 在每一象限内 , y随x的增大而增大
双曲线无限接近于 x、y 轴, 但永远不会与坐标轴相交
形状
位置
增减性
变化趋势
课堂总结
