沪教版(上海)初中数学八年级第一学期 18.4 函数的表示法 课件(42张)
文档属性
| 名称 | 沪教版(上海)初中数学八年级第一学期 18.4 函数的表示法 课件(42张) |

|
|
| 格式 | ppt | ||
| 文件大小 | 3.6MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-12-26 00:00:00 | ||
图片预览




文档简介
函数的表示法
初中我们学习过,函数的表示方法通常有 种,它们是
、 和 。
列表法
图像法
解析法
三
在研究函数的过程中,采用不同的方法表示函数,可以从不同的角度帮助我们理解函数的性质,是研究函数的重要手段.
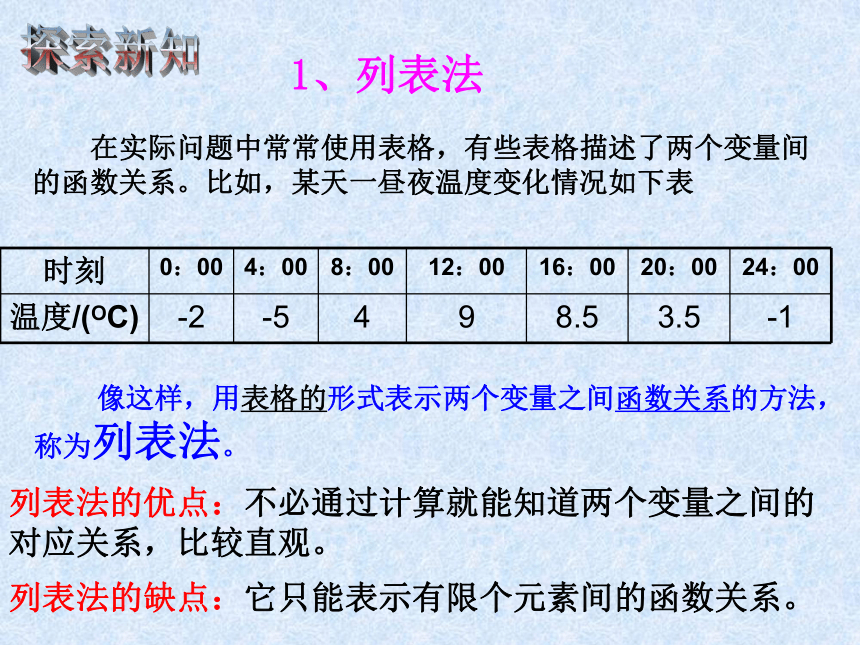
列表法的优点:不必通过计算就能知道两个变量之间的对应关系,比较直观。
在实际问题中常常使用表格,有些表格描述了两个变量间的函数关系。比如,某天一昼夜温度变化情况如下表
时刻
0:00
4:00
8:00
12:00
16:00
20:00
24:00
温度/(OC)
-2
-5
4
9
8.5
3.5
-1
像这样,用表格的形式表示两个变量之间函数关系的方法,称为列表法。
列表法的缺点:它只能表示有限个元素间的函数关系。
1、列表法
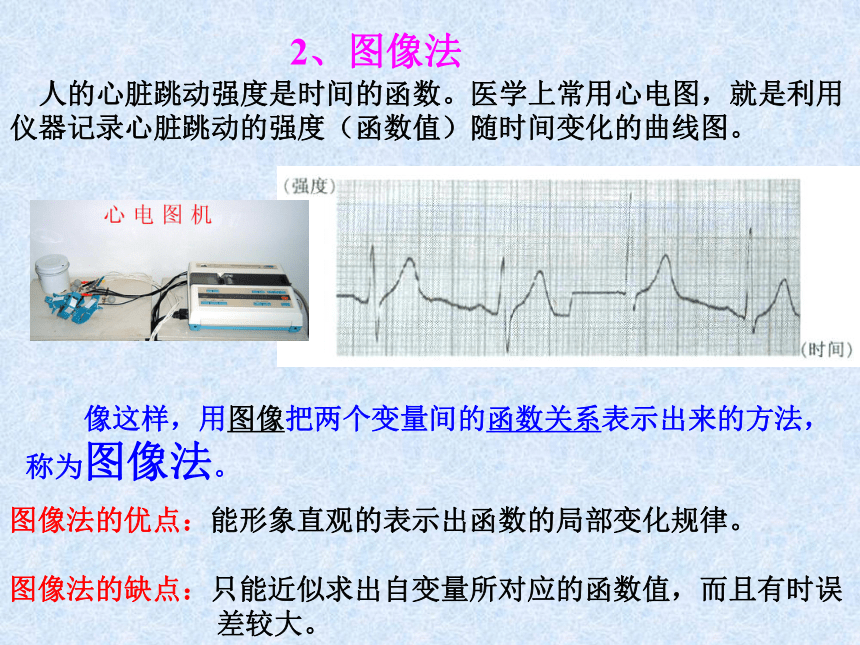
图像法的优点:能形象直观的表示出函数的局部变化规律。
人的心脏跳动强度是时间的函数。医学上常用心电图,就是利用仪器记录心脏跳动的强度(函数值)随时间变化的曲线图。
2、图像法
像这样,用图像把两个变量间的函数关系表示出来的方法,称为图像法。
图像法的缺点:只能近似求出自变量所对应的函数值,而且有时误
差较大。
把两个变量的函数关系,用一个等式表示,这个等式叫做函数的解析表达式,简称解析式。
3、解析法
正比列函数
反比列函数
一次函数
二次函数
函数解析式
一个函数的对应关系可以用自变量的解析表达式(简称解析式)表示出来,这种方法称为解析法。
解析法的优点:一是简明、全面地概括了变量间的关系;二是可以通过解析式求任意一个函数值。三是能便利研究函数性质。
解析法的缺点:不够形象、直观,而且并不是所有函数都有解析式。
解析法
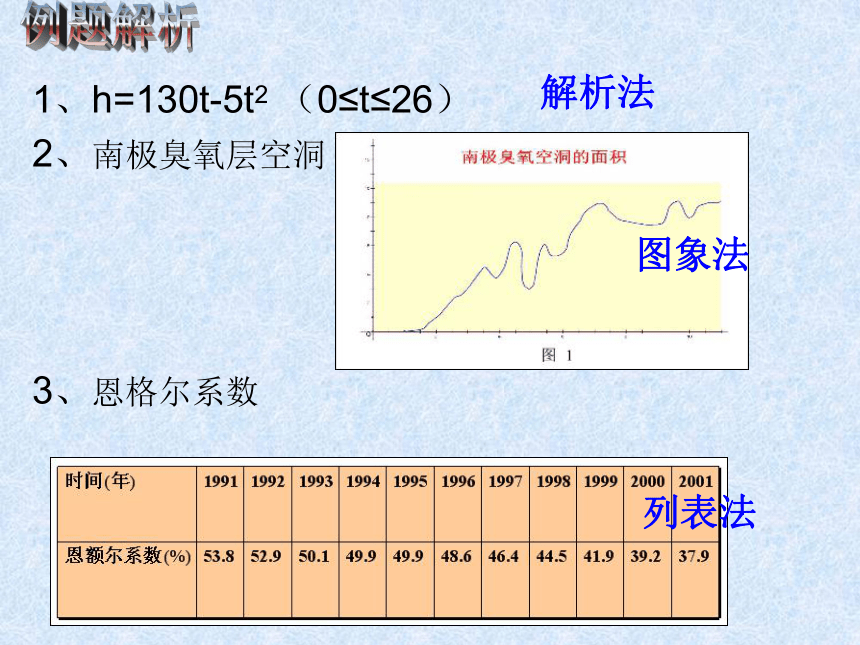
1、h=130t-5t2 (0≤t≤26)
2、南极臭氧层空洞
图象法
3、恩格尔系数
列表法
(5)气温的摄氏度数x与华氏度数y之间可以进行转化。
(6)某气象站测得当地某一天的气温变化情况如图所示:
20
2
10
8
6
4
12
18
16
14
24
22
(时)
时间t
温度T
(℃)
-2
0
2
4
6
8
(4)近年来上海市区的环境绿化不断得到改善,下表是上海市区人均绿化面积变化的一些统计数据:
年份
2000
2001
2002
2003
2004
2005
人均绿化面积(㎡)
4.5
5.5
7.0
9.4
10.0
11.0
解析法
图象法
列表法
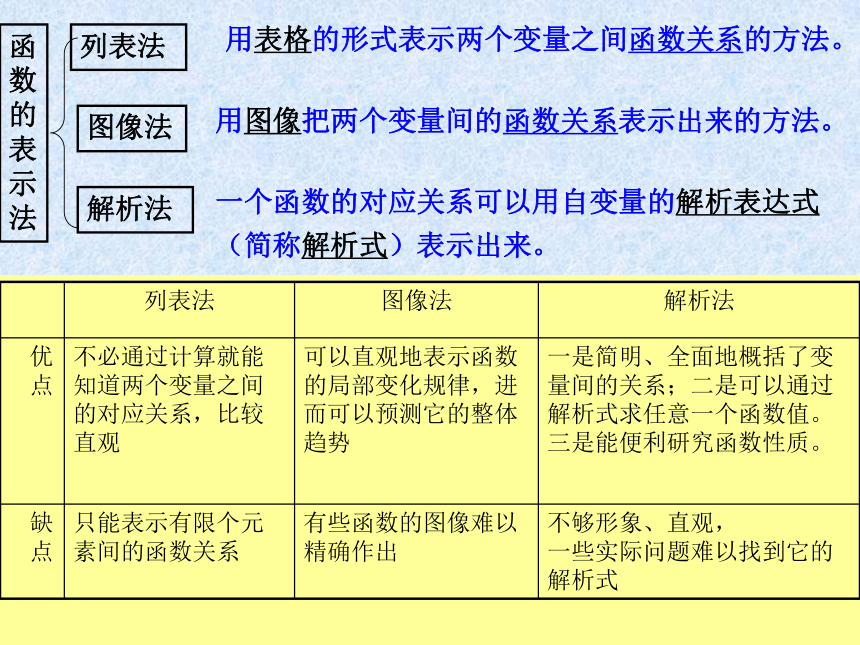
用表格的形式表示两个变量之间函数关系的方法。
用图像把两个变量间的函数关系表示出来的方法。
一个函数的对应关系可以用自变量的解析表达式(简称解析式)表示出来。
函数的表示法
列表法
图像法
解析法
列表法
图像法
解析法
优
点
不必通过计算就能知道两个变量之间的对应关系,比较直观
可以直观地表示函数的局部变化规律,进而可以预测它的整体趋势
一是简明、全面地概括了变量间的关系;二是可以通过解析式求任意一个函数值。三是能便利研究函数性质。
缺
点
只能表示有限个元素间的函数关系
有些函数的图像难以精确作出
不够形象、直观,
一些实际问题难以找到它的解析式
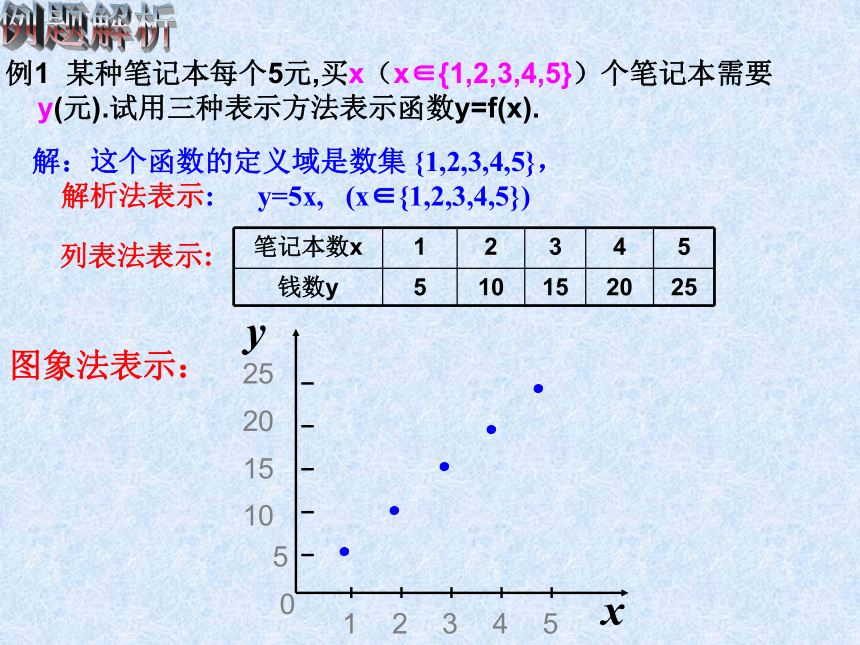
例1 某种笔记本每个5元,买x(x∈{1,2,3,4,5})个笔记本需要y(元).试用三种表示方法表示函数y=f(x).
解:这个函数的定义域是数集 {1,2,3,4,5},
解析法表示: y=5x, (x∈{1,2,3,4,5})
笔记本数x
1
2
3
4
5
钱数y
5
10
15
20
25
列表法表示:
1
2
3
4
5
0
5
10
15
20
25
.
.
.
.
.
图象法表示:
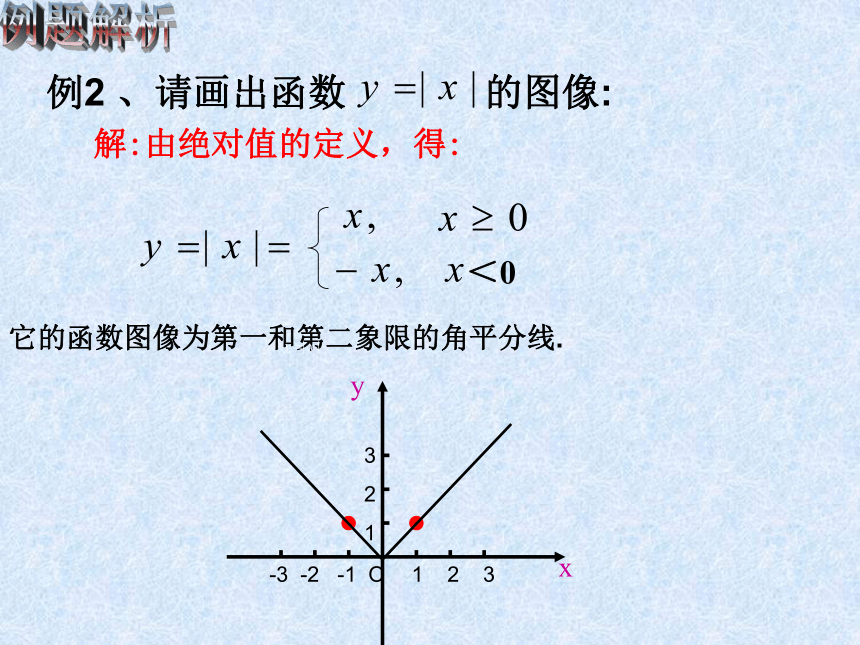
它的函数图像为第一和第二象限的角平分线.
-3 -2 -1 O
1 2 3
3
2
1
x
y
解:由绝对值的定义,得:
例2 、请画出函数 的图像:
<0
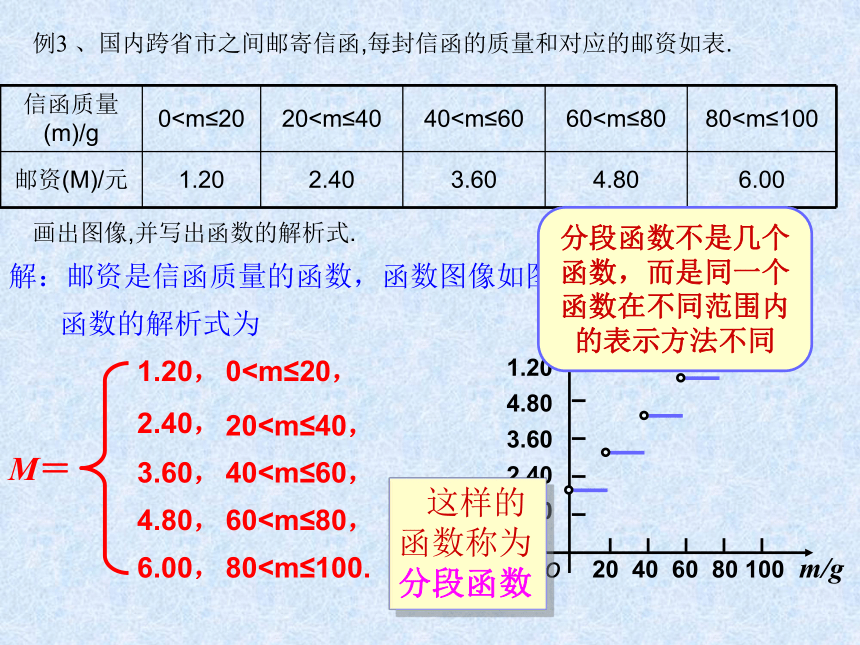
例3 、国内跨省市之间邮寄信函,每封信函的质量和对应的邮资如表.
信函质量(m)/g
020406080邮资(M)/元
1.20
2.40
3.60
4.80
6.00
画出图像,并写出函数的解析式.
解:邮资是信函质量的函数,函数图像如图。
函数的解析式为
M=
1.20,
02.40,
203.60,
404.80,
606.00,
80o 20 40 60 80 100 m/g
1.20
4.80
3.60
2.40
1.20
M/元
例3 、国内跨省市之间邮寄信函,每封信函的质量和对应的邮资如表.
信函质量(m)/g
020406080邮资(M)/元
1.20
2.40
3.60
4.80
6.00
画出图像,并写出函数的解析式.
解:邮资是信函质量的函数,函数图像如图。
函数的解析式为
M=
1.20,
02.40,
203.60,
404.80,
606.00,
80o 20 40 60 80 100 m/g
1.20
4.80
3.60
2.40
1.20
M/元
这样的函数称为分段函数
分段函数不是几个函数,而是同一个函数在不同范围内的表示方法不同
所谓“分段函数”,习惯上指在定义域的不同部分,有不同的对应法则的函数,
(1)分段函数是一个函数,不要把它误认为是几个函数;
(2)分段函数的定义域是各段定义域的并集,值域是各段值域的并集。
对它应有以下两点基本认识:
函数图象既可以是连续的曲线,也可以是直线、线段、折线、离散的点等等。
例4、某质点在30s内运动速度v是时间t的函数,它的图像如图,用解析法表示出这个函数,并求出9s时质点的速度.
t/s
v/(cm/s)
0 5 10 15 20 25 30
30
25
20
15
10
5
代入(20,30),(30,0)得
b=10
5k+b=15
设 v=kt+b
b=10
k=1
v=t+10
代入(0,10),(5,15)得
20k+b=30
30k+b=0
k=-3
b=90
v= - 3t+90
例4、某质点在30s内运动速度v是时间t的函数,它的图像如图,用解析法表示出这个函数,并求出9s时质点的速度.
t/s
v/(cm/s)
0 5 10 15 20 25 30
30
25
20
15
10
5
t∈[0,5),
t∈[5,10),
t∈[10,20),
t∈[20,30].
∵9 ∈[5,10)
∴当t=9s时,质点的速度
v(9)=3×9=27(cm/s).
解 速度是时间的函数,解析式为
求分段函数的值时,
首先应确定自变量在定义域中所在的范围;
再按相应的对应法则求值
v(2)=
v(12)=
v(20)=
v(7)=
例4、某质点在30s内运动速度v是时间t的函数,它的图像如图,用解析法表示出这个函数,并求出9s时质点的速度.
t/s
v/(cm/s)
0 5 10 15 20 25 30
30
25
20
15
10
5
v (t)=
t+10, (0 ≤ t<5),
3t, (5 ≤ t<10),
30, ( 10 ≤t <20),
t=9s时,v(9)=3×9=27 (cm/s)
-3t+90,(20 ≤ t≤30).
解: 解析式为
1.写出下列函数的定义域、值域:
(1)f(x)=3x+5;
(2)f(x)的图像如图;
x
1
2
3
4
5
6
7
8
f(x)
1
8
27
64
125
216
343
512
(3)
(1)、定义域和值域都是
(2)、定义域为
思考交流
值域为
(3)、定义域为
值域为
{1,2,3,4,5,6,7,8}
{1,8,27,64,125,216,343,512}
R
[a1,a2]∪[a3,a4]
[b4,b3]
2.下面图形是函数图像吗?
O 1
1
x
y
O 1
1
x
y
O 1
1
x
y
对于每一个自变量是不是
有唯一的值和它对应
思考交流
3.下图中可表示函数y=f(x)的图像的只可能是( )
x
y
o
x
y
o
x
y
o
x
y
o
D
思考交流
4. 设M=[0,2], N=[1,2], 在下列各图
中, 能表示f:M→N的函数
是( ).
x
x
x
x
y
y
y
y
0
0
0
0
2
2
2
2
2
2
2
2
A
B
C
D
D
思考交流
5. 已知函数f (x)=
x+2, (x≤-1)
x2, (-1<x<2)
2x, ( x≥2 )
若f(x)=3, 则x的值是( )
A. 1
B. 1或
C. 1, ,
D.
D
思考交流
如何求函数解析式
一、【配凑法(整体代换法)】
可把 看成一个整体,把右边变为由 组成的式子,再换元求出 的式子。
若已知
的表达式,欲求
的表达式,
如何求函数解析式
一、【配凑法(整体代换法)】
可把 看成一个整体,把 右边 变为由 组成的式子,再换元求出 的式子。
若已知
的表达式,欲求
的表达式,
二、【换元法】
已知
的表达式,欲求
,我们常设
等式变形
解题步骤:
④把 t 换成 x
③把 x 换成 t
②等式变形(用 t 表示 x )
②
④
③
①
①
解题时,把某个式子看成一个整体,用一个变量去代替它,从而使问题得到简化,这叫换元法。
二、【换元法】
已知
的表达式,欲求
,我们常设
解题步骤:
④把 t 换成 x
③把 x 换成 t
②等式变形(用 t 表示 x )
①
①
②
③
④
解题时,把某个式子看成一个整体,用一个变量去代替它,从而使问题得到简化,这叫换元法。
若已知 的结构时,可设出含参数的表达式,再根据已知条件,列方程或方程组,从而求出待定的参数,求得 的表达式。
三、【待定系数法】
正比列函数
反比列函数
一次函数
二次函数
由怛等式的性质,得
故所求函数的解析式为
若已知 的结构时,可设出含参数的表达式,再根据已知条件,列方程或方程组,从而求出待定的参数,求得 的表达式。
三、【待定系数法】
由怛等式的性质,得
故所求函数的解析式为
待定系数法只适用于已知所求函数类型求其解析式,
配凑法与换元法所依据的数学思想完全相同--整体思想。
配凑法
换元法
待定系数法
是求函数解析式常用的方法
四、【方程组法】
对于已知等式中出现两个不同变量的函数关系式,依据这两个变量的关系,重新建立关于这两个变量的不同等式,利用整体思想把 和另一个函数看成未知数,解方程组得函数 的解析式。此类方法类似于解二元一次方程组,故称为方程组法。
③
①
②
②×2得:
③ -①得:
代入消元法
加减消元法
四、【方程组法】
对于已知等式中出现两个不同变量的函数关系式,依据这两个变量的关系,重新建立关于这两个变量的不同等式,利用整体思想把 和另一个函数看成未知数,解方程组得函数 的解析式。此类方法类似于解二元一次方程组,故称为方程组法。
③
①
②
②×2得:
③ -①得:
五、【赋值法 (特殊值代入法)】
10
解析 主要看是否是一对多,
A
定义域分段时不能重复
思考交流
1、
解析 只有满足对任意x都有唯一的y与之对应.
D
思考交流
2、
不能一对多
8.
1、 某人去上班,由于担心迟到,因此跑着赶路,直到跑累了再走完余下的路程.如果用纵轴表示与工作单位的距离,横轴表示出发后的时间,则下列四个图像中比较符合此人走法的是( ).
解析 一开始离工作单位最远,排除A、C;开始跑得快,故在较少时间内离工作单位越来越近,故一开始时减得快,后来减得慢,即开始时倾斜程度较陡,后来较缓.
D
思考交流
3、
3.汽车经过启动、加速行驶、匀速行驶、减速行驶之后停车,若把这一过程中汽车的行驶路程s看做时间t的函数,其图像可能是( ).
解析 搞清楚汽车行驶过程中的每一阶段的路程随时间的变化情况是解题的关键.汽车经过启动、加速行驶、匀速行驶、减速行驶直至停车,在行进过程中s随时间t的增大而增大,故排除D.另外汽车在行进过程中有匀速行驶的状态,故排除C.又因为在开始时汽车启动后加速行驶的过程中行驶路程s随时间t的变化越来越快,在减速行驶直至停车的过程中行驶路程s随时间t的变化越来越慢,排除B.
A
4、
4.已知函数 f(x),g(x) 分别由下表给出:
x
1
2
3
f(x)
2
3
1
则f(g(1))=________;
x
1
2
3
g(x)
3
2
1
当g(f(x))=2时,x=________.
解析 由题意知,g(1)=3,
∵g(2)=2,
f(g(1))=
f(3)
=1
∴f(x)=2,
∴x=1.
1
1
思考交流
5、
解析 分段函数的求值问题,关键是将自变量对应到相应的“段”,然后代入求解.
思考交流
6、
-3
思考交流
7、
5.已知函数f(x)的图象如图所示,则此函
数的定义域是 ,值域是 .
【解析】由图象可看出 -3≤x≤3,-2≤y≤2
[-2,2]
[-3,3]
思考交流
8、
解:(1)、f(x)的定义域为
{x|x≤-1}
∪
{x|-1<x≤1}
∪
{x|x>1}
=R
f(x)的值域为
{y|y≤-2}
∪
{1}
∪
{y|y<-2}
={y|y≤-2或y=1}
∴f(x)的定义域为R,值域为{y|y≤-2或y=1}.
思考交流
9、
初中我们学习过,函数的表示方法通常有 种,它们是
、 和 。
列表法
图像法
解析法
三
在研究函数的过程中,采用不同的方法表示函数,可以从不同的角度帮助我们理解函数的性质,是研究函数的重要手段.
列表法的优点:不必通过计算就能知道两个变量之间的对应关系,比较直观。
在实际问题中常常使用表格,有些表格描述了两个变量间的函数关系。比如,某天一昼夜温度变化情况如下表
时刻
0:00
4:00
8:00
12:00
16:00
20:00
24:00
温度/(OC)
-2
-5
4
9
8.5
3.5
-1
像这样,用表格的形式表示两个变量之间函数关系的方法,称为列表法。
列表法的缺点:它只能表示有限个元素间的函数关系。
1、列表法
图像法的优点:能形象直观的表示出函数的局部变化规律。
人的心脏跳动强度是时间的函数。医学上常用心电图,就是利用仪器记录心脏跳动的强度(函数值)随时间变化的曲线图。
2、图像法
像这样,用图像把两个变量间的函数关系表示出来的方法,称为图像法。
图像法的缺点:只能近似求出自变量所对应的函数值,而且有时误
差较大。
把两个变量的函数关系,用一个等式表示,这个等式叫做函数的解析表达式,简称解析式。
3、解析法
正比列函数
反比列函数
一次函数
二次函数
函数解析式
一个函数的对应关系可以用自变量的解析表达式(简称解析式)表示出来,这种方法称为解析法。
解析法的优点:一是简明、全面地概括了变量间的关系;二是可以通过解析式求任意一个函数值。三是能便利研究函数性质。
解析法的缺点:不够形象、直观,而且并不是所有函数都有解析式。
解析法
1、h=130t-5t2 (0≤t≤26)
2、南极臭氧层空洞
图象法
3、恩格尔系数
列表法
(5)气温的摄氏度数x与华氏度数y之间可以进行转化。
(6)某气象站测得当地某一天的气温变化情况如图所示:
20
2
10
8
6
4
12
18
16
14
24
22
(时)
时间t
温度T
(℃)
-2
0
2
4
6
8
(4)近年来上海市区的环境绿化不断得到改善,下表是上海市区人均绿化面积变化的一些统计数据:
年份
2000
2001
2002
2003
2004
2005
人均绿化面积(㎡)
4.5
5.5
7.0
9.4
10.0
11.0
解析法
图象法
列表法
用表格的形式表示两个变量之间函数关系的方法。
用图像把两个变量间的函数关系表示出来的方法。
一个函数的对应关系可以用自变量的解析表达式(简称解析式)表示出来。
函数的表示法
列表法
图像法
解析法
列表法
图像法
解析法
优
点
不必通过计算就能知道两个变量之间的对应关系,比较直观
可以直观地表示函数的局部变化规律,进而可以预测它的整体趋势
一是简明、全面地概括了变量间的关系;二是可以通过解析式求任意一个函数值。三是能便利研究函数性质。
缺
点
只能表示有限个元素间的函数关系
有些函数的图像难以精确作出
不够形象、直观,
一些实际问题难以找到它的解析式
例1 某种笔记本每个5元,买x(x∈{1,2,3,4,5})个笔记本需要y(元).试用三种表示方法表示函数y=f(x).
解:这个函数的定义域是数集 {1,2,3,4,5},
解析法表示: y=5x, (x∈{1,2,3,4,5})
笔记本数x
1
2
3
4
5
钱数y
5
10
15
20
25
列表法表示:
1
2
3
4
5
0
5
10
15
20
25
.
.
.
.
.
图象法表示:
它的函数图像为第一和第二象限的角平分线.
-3 -2 -1 O
1 2 3
3
2
1
x
y
解:由绝对值的定义,得:
例2 、请画出函数 的图像:
<0
例3 、国内跨省市之间邮寄信函,每封信函的质量和对应的邮资如表.
信函质量(m)/g
0
1.20
2.40
3.60
4.80
6.00
画出图像,并写出函数的解析式.
解:邮资是信函质量的函数,函数图像如图。
函数的解析式为
M=
1.20,
0
20
40
60
80
1.20
4.80
3.60
2.40
1.20
M/元
例3 、国内跨省市之间邮寄信函,每封信函的质量和对应的邮资如表.
信函质量(m)/g
0
1.20
2.40
3.60
4.80
6.00
画出图像,并写出函数的解析式.
解:邮资是信函质量的函数,函数图像如图。
函数的解析式为
M=
1.20,
0
20
40
60
80
1.20
4.80
3.60
2.40
1.20
M/元
这样的函数称为分段函数
分段函数不是几个函数,而是同一个函数在不同范围内的表示方法不同
所谓“分段函数”,习惯上指在定义域的不同部分,有不同的对应法则的函数,
(1)分段函数是一个函数,不要把它误认为是几个函数;
(2)分段函数的定义域是各段定义域的并集,值域是各段值域的并集。
对它应有以下两点基本认识:
函数图象既可以是连续的曲线,也可以是直线、线段、折线、离散的点等等。
例4、某质点在30s内运动速度v是时间t的函数,它的图像如图,用解析法表示出这个函数,并求出9s时质点的速度.
t/s
v/(cm/s)
0 5 10 15 20 25 30
30
25
20
15
10
5
代入(20,30),(30,0)得
b=10
5k+b=15
设 v=kt+b
b=10
k=1
v=t+10
代入(0,10),(5,15)得
20k+b=30
30k+b=0
k=-3
b=90
v= - 3t+90
例4、某质点在30s内运动速度v是时间t的函数,它的图像如图,用解析法表示出这个函数,并求出9s时质点的速度.
t/s
v/(cm/s)
0 5 10 15 20 25 30
30
25
20
15
10
5
t∈[0,5),
t∈[5,10),
t∈[10,20),
t∈[20,30].
∵9 ∈[5,10)
∴当t=9s时,质点的速度
v(9)=3×9=27(cm/s).
解 速度是时间的函数,解析式为
求分段函数的值时,
首先应确定自变量在定义域中所在的范围;
再按相应的对应法则求值
v(2)=
v(12)=
v(20)=
v(7)=
例4、某质点在30s内运动速度v是时间t的函数,它的图像如图,用解析法表示出这个函数,并求出9s时质点的速度.
t/s
v/(cm/s)
0 5 10 15 20 25 30
30
25
20
15
10
5
v (t)=
t+10, (0 ≤ t<5),
3t, (5 ≤ t<10),
30, ( 10 ≤t <20),
t=9s时,v(9)=3×9=27 (cm/s)
-3t+90,(20 ≤ t≤30).
解: 解析式为
1.写出下列函数的定义域、值域:
(1)f(x)=3x+5;
(2)f(x)的图像如图;
x
1
2
3
4
5
6
7
8
f(x)
1
8
27
64
125
216
343
512
(3)
(1)、定义域和值域都是
(2)、定义域为
思考交流
值域为
(3)、定义域为
值域为
{1,2,3,4,5,6,7,8}
{1,8,27,64,125,216,343,512}
R
[a1,a2]∪[a3,a4]
[b4,b3]
2.下面图形是函数图像吗?
O 1
1
x
y
O 1
1
x
y
O 1
1
x
y
对于每一个自变量是不是
有唯一的值和它对应
思考交流
3.下图中可表示函数y=f(x)的图像的只可能是( )
x
y
o
x
y
o
x
y
o
x
y
o
D
思考交流
4. 设M=[0,2], N=[1,2], 在下列各图
中, 能表示f:M→N的函数
是( ).
x
x
x
x
y
y
y
y
0
0
0
0
2
2
2
2
2
2
2
2
A
B
C
D
D
思考交流
5. 已知函数f (x)=
x+2, (x≤-1)
x2, (-1<x<2)
2x, ( x≥2 )
若f(x)=3, 则x的值是( )
A. 1
B. 1或
C. 1, ,
D.
D
思考交流
如何求函数解析式
一、【配凑法(整体代换法)】
可把 看成一个整体,把右边变为由 组成的式子,再换元求出 的式子。
若已知
的表达式,欲求
的表达式,
如何求函数解析式
一、【配凑法(整体代换法)】
可把 看成一个整体,把 右边 变为由 组成的式子,再换元求出 的式子。
若已知
的表达式,欲求
的表达式,
二、【换元法】
已知
的表达式,欲求
,我们常设
等式变形
解题步骤:
④把 t 换成 x
③把 x 换成 t
②等式变形(用 t 表示 x )
②
④
③
①
①
解题时,把某个式子看成一个整体,用一个变量去代替它,从而使问题得到简化,这叫换元法。
二、【换元法】
已知
的表达式,欲求
,我们常设
解题步骤:
④把 t 换成 x
③把 x 换成 t
②等式变形(用 t 表示 x )
①
①
②
③
④
解题时,把某个式子看成一个整体,用一个变量去代替它,从而使问题得到简化,这叫换元法。
若已知 的结构时,可设出含参数的表达式,再根据已知条件,列方程或方程组,从而求出待定的参数,求得 的表达式。
三、【待定系数法】
正比列函数
反比列函数
一次函数
二次函数
由怛等式的性质,得
故所求函数的解析式为
若已知 的结构时,可设出含参数的表达式,再根据已知条件,列方程或方程组,从而求出待定的参数,求得 的表达式。
三、【待定系数法】
由怛等式的性质,得
故所求函数的解析式为
待定系数法只适用于已知所求函数类型求其解析式,
配凑法与换元法所依据的数学思想完全相同--整体思想。
配凑法
换元法
待定系数法
是求函数解析式常用的方法
四、【方程组法】
对于已知等式中出现两个不同变量的函数关系式,依据这两个变量的关系,重新建立关于这两个变量的不同等式,利用整体思想把 和另一个函数看成未知数,解方程组得函数 的解析式。此类方法类似于解二元一次方程组,故称为方程组法。
③
①
②
②×2得:
③ -①得:
代入消元法
加减消元法
四、【方程组法】
对于已知等式中出现两个不同变量的函数关系式,依据这两个变量的关系,重新建立关于这两个变量的不同等式,利用整体思想把 和另一个函数看成未知数,解方程组得函数 的解析式。此类方法类似于解二元一次方程组,故称为方程组法。
③
①
②
②×2得:
③ -①得:
五、【赋值法 (特殊值代入法)】
10
解析 主要看是否是一对多,
A
定义域分段时不能重复
思考交流
1、
解析 只有满足对任意x都有唯一的y与之对应.
D
思考交流
2、
不能一对多
8.
1、 某人去上班,由于担心迟到,因此跑着赶路,直到跑累了再走完余下的路程.如果用纵轴表示与工作单位的距离,横轴表示出发后的时间,则下列四个图像中比较符合此人走法的是( ).
解析 一开始离工作单位最远,排除A、C;开始跑得快,故在较少时间内离工作单位越来越近,故一开始时减得快,后来减得慢,即开始时倾斜程度较陡,后来较缓.
D
思考交流
3、
3.汽车经过启动、加速行驶、匀速行驶、减速行驶之后停车,若把这一过程中汽车的行驶路程s看做时间t的函数,其图像可能是( ).
解析 搞清楚汽车行驶过程中的每一阶段的路程随时间的变化情况是解题的关键.汽车经过启动、加速行驶、匀速行驶、减速行驶直至停车,在行进过程中s随时间t的增大而增大,故排除D.另外汽车在行进过程中有匀速行驶的状态,故排除C.又因为在开始时汽车启动后加速行驶的过程中行驶路程s随时间t的变化越来越快,在减速行驶直至停车的过程中行驶路程s随时间t的变化越来越慢,排除B.
A
4、
4.已知函数 f(x),g(x) 分别由下表给出:
x
1
2
3
f(x)
2
3
1
则f(g(1))=________;
x
1
2
3
g(x)
3
2
1
当g(f(x))=2时,x=________.
解析 由题意知,g(1)=3,
∵g(2)=2,
f(g(1))=
f(3)
=1
∴f(x)=2,
∴x=1.
1
1
思考交流
5、
解析 分段函数的求值问题,关键是将自变量对应到相应的“段”,然后代入求解.
思考交流
6、
-3
思考交流
7、
5.已知函数f(x)的图象如图所示,则此函
数的定义域是 ,值域是 .
【解析】由图象可看出 -3≤x≤3,-2≤y≤2
[-2,2]
[-3,3]
思考交流
8、
解:(1)、f(x)的定义域为
{x|x≤-1}
∪
{x|-1<x≤1}
∪
{x|x>1}
=R
f(x)的值域为
{y|y≤-2}
∪
{1}
∪
{y|y<-2}
={y|y≤-2或y=1}
∴f(x)的定义域为R,值域为{y|y≤-2或y=1}.
思考交流
9、
