沪教版(上海)初中数学八年级第一学期 18.4 函数的表示法 课件(18张)
文档属性
| 名称 | 沪教版(上海)初中数学八年级第一学期 18.4 函数的表示法 课件(18张) |

|
|
| 格式 | ppt | ||
| 文件大小 | 1.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-12-26 00:00:00 | ||
图片预览




文档简介
1:我们学习了正比例函数、反比例函数,它们的一般式是怎样的?
两个变量之间的依赖关系用数学式子来表达,这种表示函数的方法叫做解析法.
函数解析式
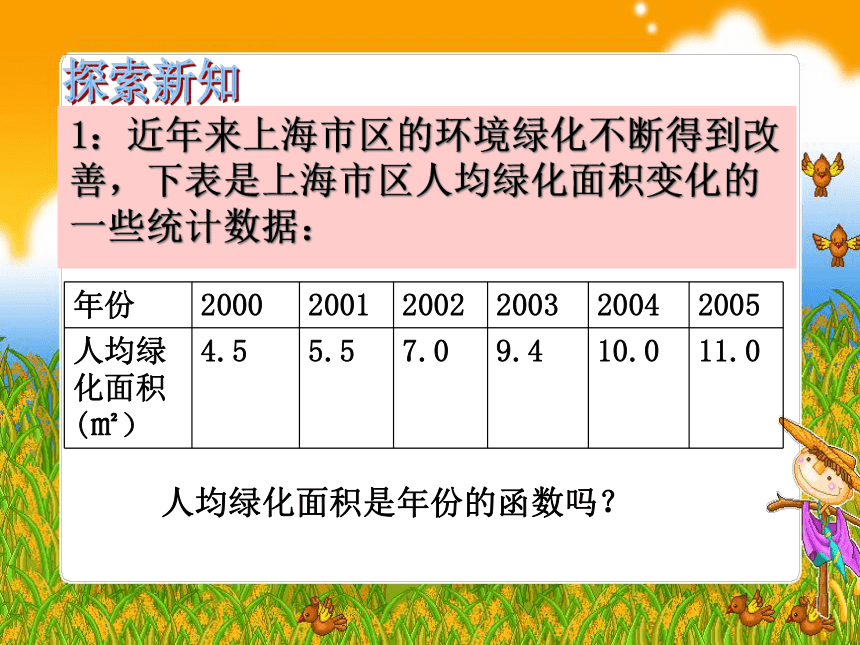
1:近年来上海市区的环境绿化不断得到改善,下表是上海市区人均绿化面积变化的一些统计数据:
年份
2000
2001
2002
2003
2004
2005
人均绿化面积(㎡)
4.5
5.5
7.0
9.4
10.0
11.0
人均绿化面积是年份的函数吗?
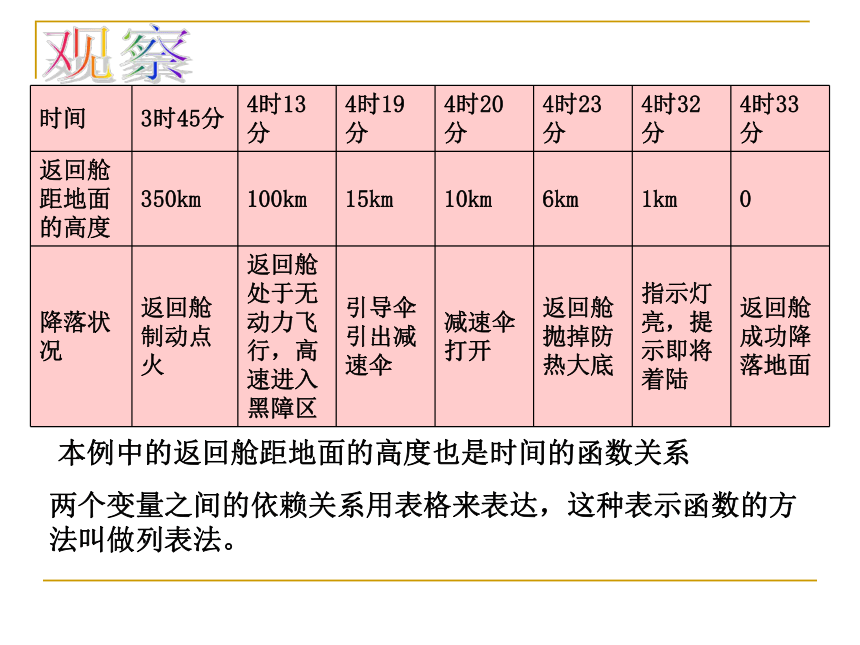
2005年10月17日, “神舟”六号载人飞船顺利返回地面。下面是“神舟” 飞船返回舱返回过程中的相关记录:
时间
3时45分
4时13分
4时19分
4时20分
4时23分
4时32分
4时33分
返回舱距地面的高度
350km
100km
15km
10km
6km
1km
0
降落状况
返回舱制动点火
返回舱处于无动力飞行,高速进入黑障区
引导伞引出减速伞
减速伞打开
返回舱抛掉防热大底
指示灯亮,提示即将着陆
返回舱成功降落地面
本例中的返回舱距地面的高度也是时间的函数关系
两个变量之间的依赖关系用表格来表达,这种表示函数的方法叫做列表法。
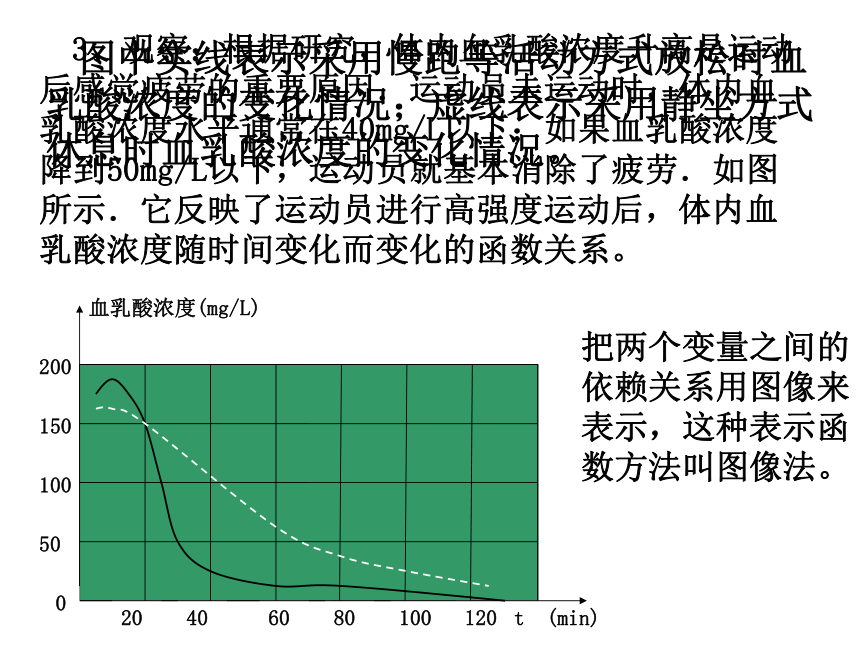
3、观察:根据研究,体内血乳酸浓度升高是运动后感觉疲劳的重要原因.运动员未运动时,体内血乳酸浓度水平通常在40mg/L以下;如果血乳酸浓度降到50mg/L以下,运动员就基本消除了疲劳.如图所示.它反映了运动员进行高强度运动后,体内血乳酸浓度随时间变化而变化的函数关系。
50
100
150
200
20
40
60
80
100
120
t (min)
血乳酸浓度(mg/L)
0
图中实线表示采用慢跑等活动方式放松时血乳酸浓度的变化情况;虚线表示采用静坐方式休息时血乳酸浓度的变化情况。
把两个变量之间的依赖关系用图像来表示,这种表示函数方法叫图像法。
今天我们学习了哪几种函数的常用表示方法?
解析法、列表法、图像法
接下来我们一起说说这几种函数表示法的优缺点:
年份
2000
2001
2002
2003
2004
2005
人均绿化面积(㎡)
4.5
5.5
7.0
9.4
10.0
11.0
50
100
150
200
20
40
60
80
100
120
t (min)
血乳酸浓度(mg/L)
0
函数的表示法
优点
缺点
解析法
简单明了
不能表示所有的函数
列表法
一目了然,查找方便
列不出所有的数值
图像法
直观清晰,变化趋势容易看清楚
不精确,列不出所有的数值,有些画不出完整图像
用适当的方法表示函数,或者把几种方法结合起来,能够帮助我们更好的理解函数和运用函数解决问题
例1:一位学生在乘坐磁悬浮列车从龙阳路站到上海浦东国际机场途中,记录了车运行速度的变化情况,如下表:
时间t(分)
0
1
1.5
2
3
4
5
5.5
6
7
8
速度v(千米/时)
0
146
217
300
300
300
300
300
281
121
0
根据表中提供的信息回答下列问题:
(1)在哪一段时间内列车的速度逐渐加快?在哪一段时间内列车的速度逐渐减慢?
(2)在哪一段时间内列车是匀速行驶的?在这一段时间内列车走了多少路程?
例2:把一块边长是20厘米的正方形铁皮,在四角各截去边长为x厘米的小正方形,再按虚线折成一个无盖的长方体盒子。求这个盒子的容积V
(立方厘米)关于x
(厘米)的函数解析
式以及函数的定义域。
x
x
20-2x
20
1:某校生物小组学生准备在校内一空地围一个长方形苗圃,苗圃的一边靠墙长为x米,苗圃的另一边与墙垂直,长为30米,墙可利用部分的最大长度为40米;请写出苗圃的面积y(平方米)与靠墙一边的长x(米)的函数解析式以及函数的定义域。
例 3:2014年5月以来,我国南方地区持续强暴雨,引发洪涝灾害,图2是下游地区水文站记录的某天9时至21时河水水位的变化情况
1:在图2中,河水水位与时间的函数关系是用什么方法表示的?
2:你能看出哪一时刻河水的水位最高吗?
3:最高水位是多少?
4:当天17时的河水
水位是多少?
11时
93m
85m
93
85
图像法
例4 如图:甲于
12时30分骑自行车
从A地出发前往B地,乙骑摩托车从A地
出发前往B。图中
的折线PQR和线段
MN分别反映了甲和
乙所行驶的路程s与
该日下午的时间t的
函数关系。
o
5
20
15
10
25
1
2
P
Q
R
M
N
S(千米)
下午t(时)
你能从图中读出哪些信息?
例4:图中的折线PQR
和线段MN分别反映
了甲和乙所行驶的
路程s与该日下午
的时间t的函数关系
o
5
20
15
10
25
1
2
P
Q
R
M
N
S(千米)
下午t
(时)
(1)甲出发后几小时乙才出发?
(2)乙行驶多少分钟后追上甲?这时两人离B地还有多少千米?
(3)甲乙两人分别在下午几点到达B地?
(4)甲从下午1时到2时半的速度是每小时多少千米?
(5)乙的速度是每小时多少千米?
作业:1:练习册18.4(1)2:选做思考题
1、一个有进、出水管的容器,单位时间内进、出水量都是一定。设从某时刻开始4分钟内只进水不出水,之后的4分钟只出水不进水,得到的时间x(分钟)和水量y(升)之间的关系如图:
O
4
8
16
20
x(分钟)
y(升)
求:(1)每分钟进多少升水?
(2)每分钟出多少升水?
(3) 时,y关于x的解析式。
2、某工厂修建了甲乙两个水池,最大蓄水量都是1200立方米。若甲池有水480立方米,乙池蓄满了水,甲池每小时进水80立方米,乙池每小时放水100立方米。
(1)分别写出甲乙两池内水量y与时间t之间的函数关系式
(2)问:甲乙两池同时进水或放水,经过几个小时两个池内的水量一样多?
路程
(千米)
时间(小时)
O
10
30
20
50
40
60
70
80
100
90
自行车
摩托车
1
2
3
4
6
7
5
8
3、甲乙两人(甲骑自行车,乙骑摩托)从A城出发到B城旅行。如图表示两人离开A城的路程与时间之间的函数图像。从图像中,你能得到关于甲乙两人旅行的哪些信息?(尽可能多)
两个变量之间的依赖关系用数学式子来表达,这种表示函数的方法叫做解析法.
函数解析式
1:近年来上海市区的环境绿化不断得到改善,下表是上海市区人均绿化面积变化的一些统计数据:
年份
2000
2001
2002
2003
2004
2005
人均绿化面积(㎡)
4.5
5.5
7.0
9.4
10.0
11.0
人均绿化面积是年份的函数吗?
2005年10月17日, “神舟”六号载人飞船顺利返回地面。下面是“神舟” 飞船返回舱返回过程中的相关记录:
时间
3时45分
4时13分
4时19分
4时20分
4时23分
4时32分
4时33分
返回舱距地面的高度
350km
100km
15km
10km
6km
1km
0
降落状况
返回舱制动点火
返回舱处于无动力飞行,高速进入黑障区
引导伞引出减速伞
减速伞打开
返回舱抛掉防热大底
指示灯亮,提示即将着陆
返回舱成功降落地面
本例中的返回舱距地面的高度也是时间的函数关系
两个变量之间的依赖关系用表格来表达,这种表示函数的方法叫做列表法。
3、观察:根据研究,体内血乳酸浓度升高是运动后感觉疲劳的重要原因.运动员未运动时,体内血乳酸浓度水平通常在40mg/L以下;如果血乳酸浓度降到50mg/L以下,运动员就基本消除了疲劳.如图所示.它反映了运动员进行高强度运动后,体内血乳酸浓度随时间变化而变化的函数关系。
50
100
150
200
20
40
60
80
100
120
t (min)
血乳酸浓度(mg/L)
0
图中实线表示采用慢跑等活动方式放松时血乳酸浓度的变化情况;虚线表示采用静坐方式休息时血乳酸浓度的变化情况。
把两个变量之间的依赖关系用图像来表示,这种表示函数方法叫图像法。
今天我们学习了哪几种函数的常用表示方法?
解析法、列表法、图像法
接下来我们一起说说这几种函数表示法的优缺点:
年份
2000
2001
2002
2003
2004
2005
人均绿化面积(㎡)
4.5
5.5
7.0
9.4
10.0
11.0
50
100
150
200
20
40
60
80
100
120
t (min)
血乳酸浓度(mg/L)
0
函数的表示法
优点
缺点
解析法
简单明了
不能表示所有的函数
列表法
一目了然,查找方便
列不出所有的数值
图像法
直观清晰,变化趋势容易看清楚
不精确,列不出所有的数值,有些画不出完整图像
用适当的方法表示函数,或者把几种方法结合起来,能够帮助我们更好的理解函数和运用函数解决问题
例1:一位学生在乘坐磁悬浮列车从龙阳路站到上海浦东国际机场途中,记录了车运行速度的变化情况,如下表:
时间t(分)
0
1
1.5
2
3
4
5
5.5
6
7
8
速度v(千米/时)
0
146
217
300
300
300
300
300
281
121
0
根据表中提供的信息回答下列问题:
(1)在哪一段时间内列车的速度逐渐加快?在哪一段时间内列车的速度逐渐减慢?
(2)在哪一段时间内列车是匀速行驶的?在这一段时间内列车走了多少路程?
例2:把一块边长是20厘米的正方形铁皮,在四角各截去边长为x厘米的小正方形,再按虚线折成一个无盖的长方体盒子。求这个盒子的容积V
(立方厘米)关于x
(厘米)的函数解析
式以及函数的定义域。
x
x
20-2x
20
1:某校生物小组学生准备在校内一空地围一个长方形苗圃,苗圃的一边靠墙长为x米,苗圃的另一边与墙垂直,长为30米,墙可利用部分的最大长度为40米;请写出苗圃的面积y(平方米)与靠墙一边的长x(米)的函数解析式以及函数的定义域。
例 3:2014年5月以来,我国南方地区持续强暴雨,引发洪涝灾害,图2是下游地区水文站记录的某天9时至21时河水水位的变化情况
1:在图2中,河水水位与时间的函数关系是用什么方法表示的?
2:你能看出哪一时刻河水的水位最高吗?
3:最高水位是多少?
4:当天17时的河水
水位是多少?
11时
93m
85m
93
85
图像法
例4 如图:甲于
12时30分骑自行车
从A地出发前往B地,乙骑摩托车从A地
出发前往B。图中
的折线PQR和线段
MN分别反映了甲和
乙所行驶的路程s与
该日下午的时间t的
函数关系。
o
5
20
15
10
25
1
2
P
Q
R
M
N
S(千米)
下午t(时)
你能从图中读出哪些信息?
例4:图中的折线PQR
和线段MN分别反映
了甲和乙所行驶的
路程s与该日下午
的时间t的函数关系
o
5
20
15
10
25
1
2
P
Q
R
M
N
S(千米)
下午t
(时)
(1)甲出发后几小时乙才出发?
(2)乙行驶多少分钟后追上甲?这时两人离B地还有多少千米?
(3)甲乙两人分别在下午几点到达B地?
(4)甲从下午1时到2时半的速度是每小时多少千米?
(5)乙的速度是每小时多少千米?
作业:1:练习册18.4(1)2:选做思考题
1、一个有进、出水管的容器,单位时间内进、出水量都是一定。设从某时刻开始4分钟内只进水不出水,之后的4分钟只出水不进水,得到的时间x(分钟)和水量y(升)之间的关系如图:
O
4
8
16
20
x(分钟)
y(升)
求:(1)每分钟进多少升水?
(2)每分钟出多少升水?
(3) 时,y关于x的解析式。
2、某工厂修建了甲乙两个水池,最大蓄水量都是1200立方米。若甲池有水480立方米,乙池蓄满了水,甲池每小时进水80立方米,乙池每小时放水100立方米。
(1)分别写出甲乙两池内水量y与时间t之间的函数关系式
(2)问:甲乙两池同时进水或放水,经过几个小时两个池内的水量一样多?
路程
(千米)
时间(小时)
O
10
30
20
50
40
60
70
80
100
90
自行车
摩托车
1
2
3
4
6
7
5
8
3、甲乙两人(甲骑自行车,乙骑摩托)从A城出发到B城旅行。如图表示两人离开A城的路程与时间之间的函数图像。从图像中,你能得到关于甲乙两人旅行的哪些信息?(尽可能多)
