沪教版(上海)初中数学八年级第一学期 19.5 角的平分线 课件(18张)
文档属性
| 名称 | 沪教版(上海)初中数学八年级第一学期 19.5 角的平分线 课件(18张) |
|
|
| 格式 | ppt | ||
| 文件大小 | 468.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-12-26 10:30:31 | ||
图片预览




文档简介
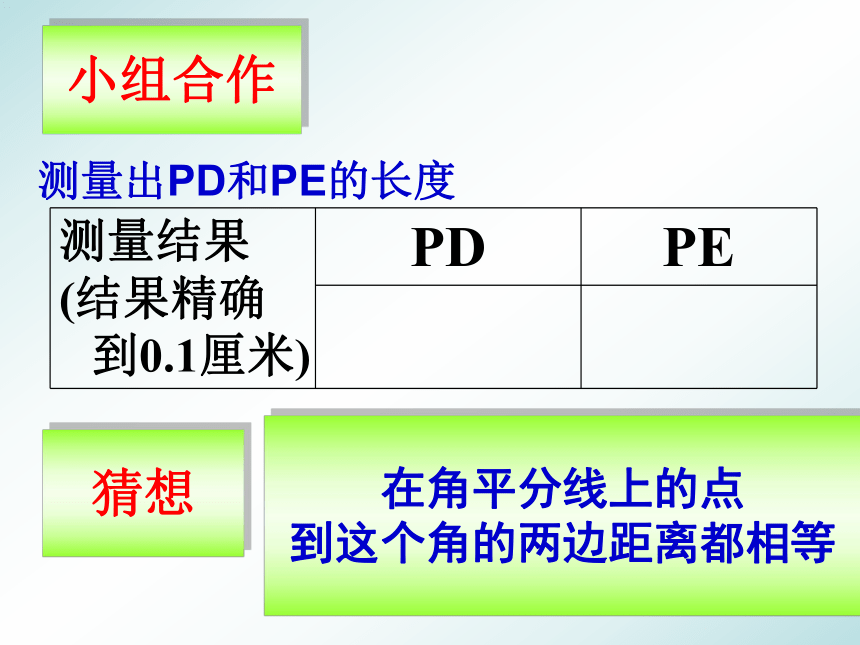
情境引入
A
O
B
折痕
角是__________________图形,
对称轴是___________________________________
轴对称
角的平分线所在的直线
19.5 角的平分线
(第一课时)
1、根据折痕,画出∠AOB的平分线OC
探究一
2、在OC上任取一点P
3、过点P作PD⊥OA,PE⊥OB, D、E为垂足
按要求作图:
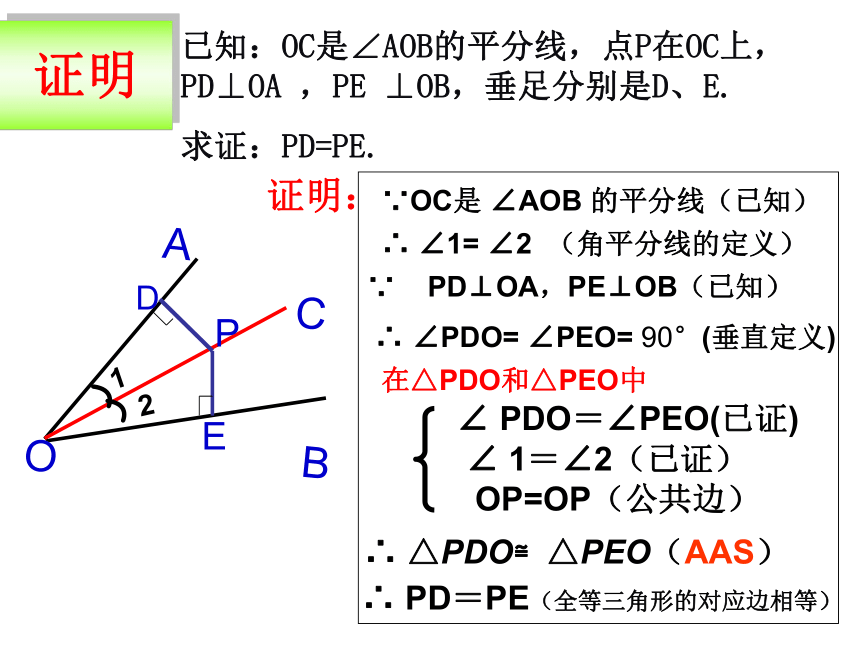
小组合作
测量出PD和PE的长度
测量结果
(结果精确到0.1厘米)
PD
PE
猜想
在角平分线上的点
到这个角的两边距离都相等
证明:
∵OC是 ∠AOB 的平分线(已知)
∴ ∠1= ∠2 (角平分线的定义)
∵ PD⊥OA,PE⊥OB(已知)
∴ ∠PDO= ∠PEO= 90°(垂直定义)
在△PDO和△PEO中
∠ PDO=∠PEO(已证)
∠ 1=∠2(已证)
OP=OP(公共边)
∴ △PDO≌△PEO(AAS)
∴ PD=PE(全等三角形的对应边相等)
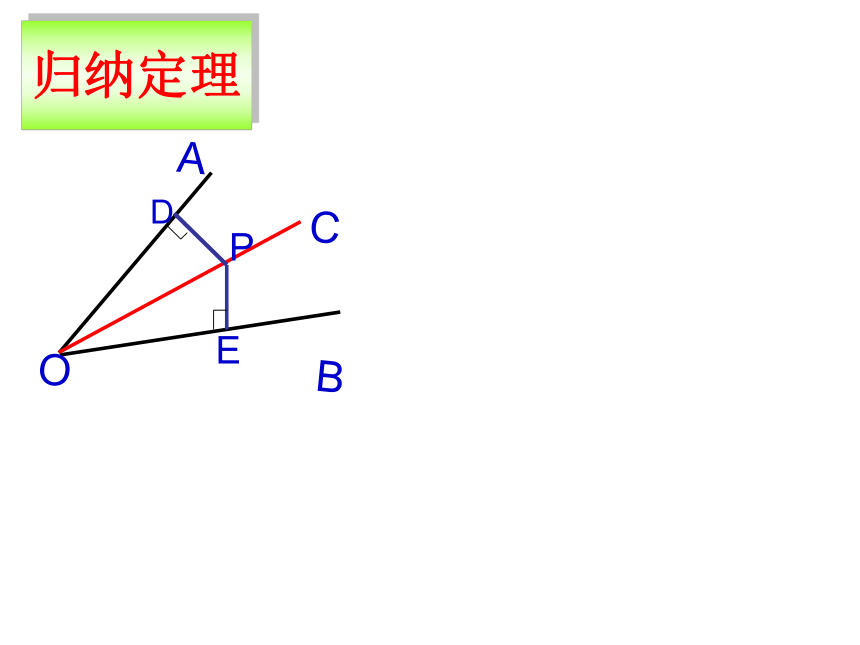
已知:OC是∠AOB的平分线,点P在OC上,PD⊥OA ,PE ⊥OB,垂足分别是D、E.
求证:PD=PE.
A
O
B
C
D
E
P
1
2
证明
归纳定理
A
O
B
C
D
E
P
练习1、如图,OC是∠AOB的平分线,点P在OC上,PD⊥OA,PE⊥OB,垂足分别是D、E,PD=2cm,则PE=__________cm.
A
D
O
B
E
P
C
2
新知应用1
练习2.如图,在△ABC中,∠C=900,AD平分∠BAC交BC于点D,若BC=10,BD=7,则点D到AB的距离为_________
A
C
D
B
E
新知应用1
3
探究二
你能说说角平分线性质定理的逆命题吗?
证 明
已知:如图,PD⊥OA ,PE⊥OB ,垂足分别是D、E,PD=PE,
求证:点P在 ∠AOB 的角平分线上。
A
O
B
C
D
E
P
1
2
证明:
联结DE,
在△PDE中, ∵PD=PE(已知)
∴ ∠3= ∠4(等边对等角)
3
4
∵ PD⊥OA,PE⊥OB(已知)
∴ ∠PDO= ∠PEO= 90°(垂直定义)
∴ ∠5= ∠6(等式性质)
5
6
∴在△ODE中,OD=OE (等角对等边)
在△PDO和△PEO中
PD=PE(已知)
OP=OP(公共边)
OD=OE(已证)
∴ △PDO≌△PEO(SSS)
∴ ∠1= ∠2(全等三角形的对应角相等)
即点P在 ∠AOB 的角平分线上
归纳逆定理
A
O
B
练习3:如图,△ABC中,∠C=90°,AC=CB,点D在BC上,DE⊥AB,点E为垂足,且DE=DC,联结AD, 则∠DAB=_________度,∠ADB=_________度
A
B
C
D
E
新知应用2
112.5
22.5
例1:已知,如图,AO、BO分别是∠A, ∠B的平分线,OD ⊥ BC,OE ⊥ AB,垂足分别为点D、E
求证:点O在∠C的平分线上。
综合应用
A
B
C
O
D
E
F
三角形的 ____的交点到三角形三边的距离相等。
角平分线
如图,为了促进当地旅游发展,某地要在三条公路围成的一块平地上修建一个度假村.要使这个度假村到三条公路的距离相等,应在何处修建?
综合应用
练习4:已知如图,PB、PC分别是△ABC的外角
平分线,PM⊥AB,PN⊥AC,点M、N分别为垂足,
(1)求证:PM=PN
(2)联结PA,求证PA平分∠MAN
A
B
C
P
N
M
F
本节课你学到了哪些知识?
小结
已知:如图,在△ABC中,AD是它的角平分线且AB=AC,DE⊥AB,DF⊥AC,垂足分别是E,F.
求证:EB=FC.
B
A
E
D
C
F
课后思 考
作业
完成课堂学习单!
A
O
B
折痕
角是__________________图形,
对称轴是___________________________________
轴对称
角的平分线所在的直线
19.5 角的平分线
(第一课时)
1、根据折痕,画出∠AOB的平分线OC
探究一
2、在OC上任取一点P
3、过点P作PD⊥OA,PE⊥OB, D、E为垂足
按要求作图:
小组合作
测量出PD和PE的长度
测量结果
(结果精确到0.1厘米)
PD
PE
猜想
在角平分线上的点
到这个角的两边距离都相等
证明:
∵OC是 ∠AOB 的平分线(已知)
∴ ∠1= ∠2 (角平分线的定义)
∵ PD⊥OA,PE⊥OB(已知)
∴ ∠PDO= ∠PEO= 90°(垂直定义)
在△PDO和△PEO中
∠ PDO=∠PEO(已证)
∠ 1=∠2(已证)
OP=OP(公共边)
∴ △PDO≌△PEO(AAS)
∴ PD=PE(全等三角形的对应边相等)
已知:OC是∠AOB的平分线,点P在OC上,PD⊥OA ,PE ⊥OB,垂足分别是D、E.
求证:PD=PE.
A
O
B
C
D
E
P
1
2
证明
归纳定理
A
O
B
C
D
E
P
练习1、如图,OC是∠AOB的平分线,点P在OC上,PD⊥OA,PE⊥OB,垂足分别是D、E,PD=2cm,则PE=__________cm.
A
D
O
B
E
P
C
2
新知应用1
练习2.如图,在△ABC中,∠C=900,AD平分∠BAC交BC于点D,若BC=10,BD=7,则点D到AB的距离为_________
A
C
D
B
E
新知应用1
3
探究二
你能说说角平分线性质定理的逆命题吗?
证 明
已知:如图,PD⊥OA ,PE⊥OB ,垂足分别是D、E,PD=PE,
求证:点P在 ∠AOB 的角平分线上。
A
O
B
C
D
E
P
1
2
证明:
联结DE,
在△PDE中, ∵PD=PE(已知)
∴ ∠3= ∠4(等边对等角)
3
4
∵ PD⊥OA,PE⊥OB(已知)
∴ ∠PDO= ∠PEO= 90°(垂直定义)
∴ ∠5= ∠6(等式性质)
5
6
∴在△ODE中,OD=OE (等角对等边)
在△PDO和△PEO中
PD=PE(已知)
OP=OP(公共边)
OD=OE(已证)
∴ △PDO≌△PEO(SSS)
∴ ∠1= ∠2(全等三角形的对应角相等)
即点P在 ∠AOB 的角平分线上
归纳逆定理
A
O
B
练习3:如图,△ABC中,∠C=90°,AC=CB,点D在BC上,DE⊥AB,点E为垂足,且DE=DC,联结AD, 则∠DAB=_________度,∠ADB=_________度
A
B
C
D
E
新知应用2
112.5
22.5
例1:已知,如图,AO、BO分别是∠A, ∠B的平分线,OD ⊥ BC,OE ⊥ AB,垂足分别为点D、E
求证:点O在∠C的平分线上。
综合应用
A
B
C
O
D
E
F
三角形的 ____的交点到三角形三边的距离相等。
角平分线
如图,为了促进当地旅游发展,某地要在三条公路围成的一块平地上修建一个度假村.要使这个度假村到三条公路的距离相等,应在何处修建?
综合应用
练习4:已知如图,PB、PC分别是△ABC的外角
平分线,PM⊥AB,PN⊥AC,点M、N分别为垂足,
(1)求证:PM=PN
(2)联结PA,求证PA平分∠MAN
A
B
C
P
N
M
F
本节课你学到了哪些知识?
小结
已知:如图,在△ABC中,AD是它的角平分线且AB=AC,DE⊥AB,DF⊥AC,垂足分别是E,F.
求证:EB=FC.
B
A
E
D
C
F
课后思 考
作业
完成课堂学习单!
