沪教版(上海)初中数学八年级第一学期 19.5 角的平分线 课件(17张)
文档属性
| 名称 | 沪教版(上海)初中数学八年级第一学期 19.5 角的平分线 课件(17张) |

|
|
| 格式 | pptx | ||
| 文件大小 | 189.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-12-26 00:00:00 | ||
图片预览




文档简介
沪教标准版 数学 八年级上
19.5角的平分线
知识链接
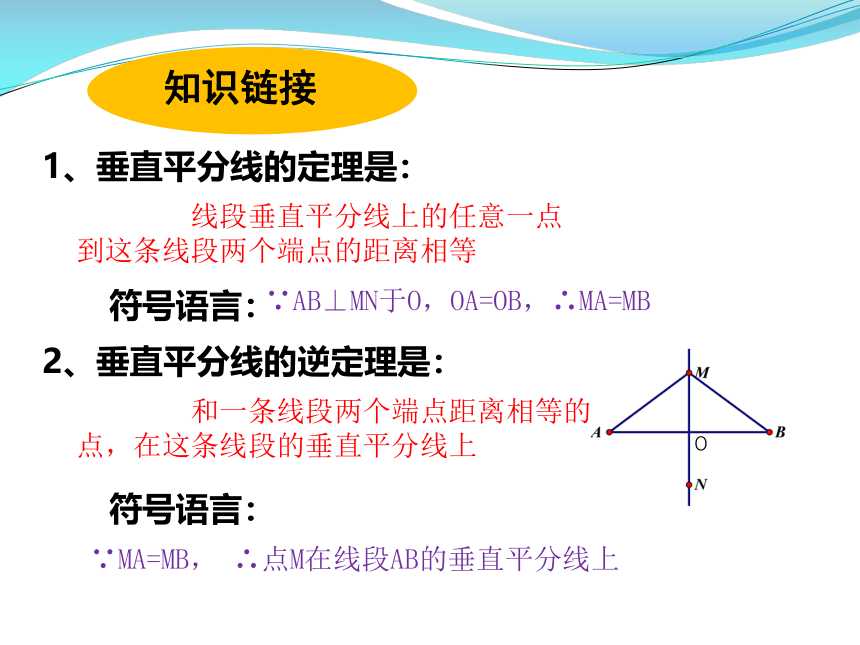
1、垂直平分线的定理是:
线段垂直平分线上的任意一点到这条线段两个端点的距离相等
2、垂直平分线的逆定理是:
符号语言:
符号语言:
∵AB⊥MN于O,OA=OB,∴MA=MB
和一条线段两个端点距离相等的点,在这条线段的垂直平分线上
∵MA=MB, ∴点M在线段AB的垂直平分线上
O
知识链接
4、点到直线的距离定义
过直线外一点作已知直线的垂线段,垂线段的长度叫作点到直线的距离。
3、全等三角形的判定定理
SSS SAS ASA AAS HL
创设情境
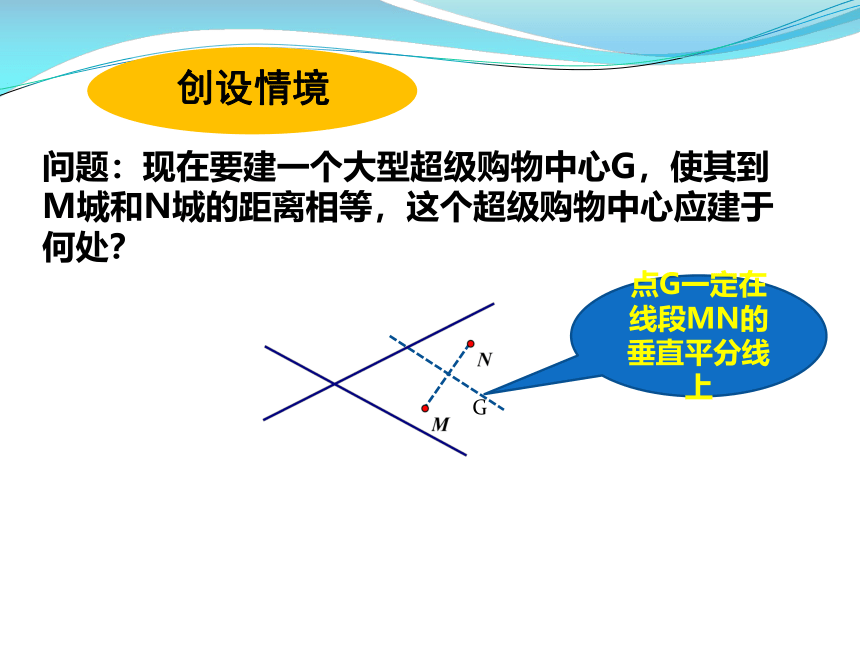
问题:现在要建一个大型超级购物中心G,使其到M城和N城的距离相等,这个超级购物中心应建于何处?
点G一定在线段MN的垂直平分线上
G
创设情境
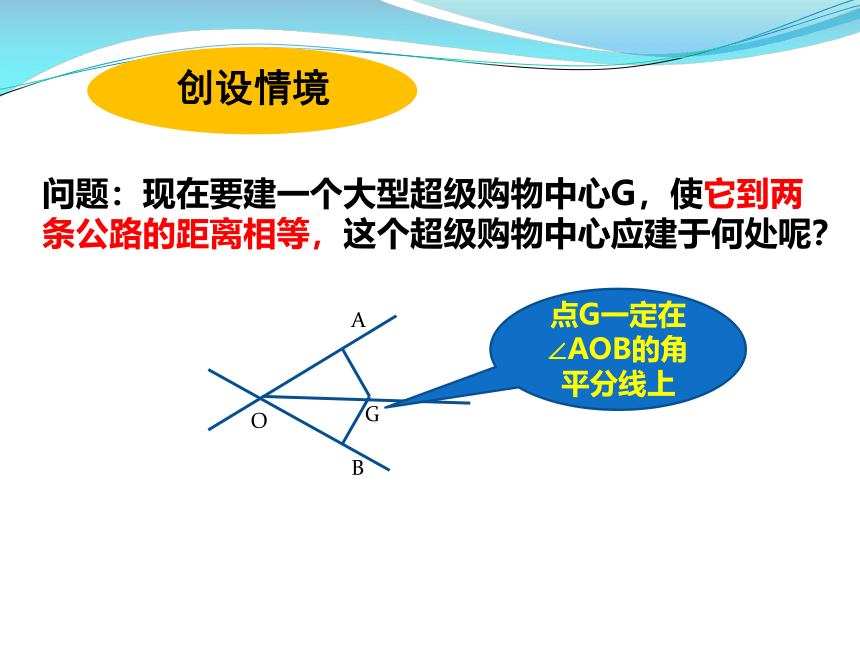
问题:现在要建一个大型超级购物中心G,使它到两条公路的距离相等,这个超级购物中心应建于何处呢?
实验探究
按下面的过程操作:
(1)准备一块三角形纸板
(2)将其中一角对折
(3)再将开口一端对折
(过程如图所示)
(4)将折好后的纸板展开观察折痕,说出图形中的各边和各角之间的关系?
(5)变换(3)步骤中折痕的位置观察上述的结论是否有变化?
创设情境
问题:现在要建一个大型超级购物中心G,使它到两条公路的距离相等,这个超级购物中心应建于何处呢?
G
点G一定在∠AOB的角平分线上
A
O
B
(5)类比垂直平分线定理说说角平分线上的点有怎样的结论?
(6)试说出已知和求证,并用理论进行证明。
实验小结
角的平分线上的点到这个角的两边的距离相等
已知:点D在∠BAC的平分线上,DB⊥AB,DC⊥AC,
求证: DB=DC
探索新知
角平分线的定理:
在角的平分线上的点到这个角的两边的距离相等
角平分有逆定理吗?
已知:DB=DC,DB⊥AB,DC⊥AC,求证:点D在∠BAC的平分线上
角的内部,到角的两边距离相等的点在这个角的平分线上
探索新知
角平分线的逆定理:
在一个角的内部(包括顶点)且到角的两边距离相等的点,在这个角的平分线上。
角平分线的定理:
在角的平分线上的点到这个角的两边的距离相等
对比角平分的定理及其逆定理,说说他们的区别。
知识对比
角平分线的定理:
角平分线
点到直线的距离相等
角平分线的逆定理:
点到直线的距离相等
角平分线
判断下列说法是否正确?如果错误请说明原因。
①已知 OC是∠AOB的角平分线,点P是OC上一点,则PD=PE. ( )
②已知点P为∠AOB内部一点,点D在OA上,点E在OB上,若PD=PE,则OC是∠AOB的角平分线. ( )
应用角平分线定理和逆定理时,垂直条件不可少
×
×
例题分析
例1 如图,AO、BO分别是∠A、∠B的平分线,OD⊥BC,OE⊥AB,垂足分别是D、E.
求证:点O在∠C的平分线上。
F
要想证明点O在∠C的平分线上
只要证明点O到∠C的两边距离相等
已知AO是∠A的平分线OE⊥AB,OF⊥AC
OE=OF
已知BO是∠B的平分线OE⊥AB,OD⊥BC
OE=OD
OD=OF
构建点O到∠C的两边距离,过点O作OF⊥AC只要证明OD=OF
思
维
导
图
角平分线逆定理
角平分线定理
角平分线定理
等量代换
角平分线问题中常见的辅助线建立方式
解题技巧:分析几何问题时要学会先在头脑中构建思维导图
已知:如图①,点P、D在∠AOB的平分线上,OA=OB,PM⊥BD,PN⊥AD,垂足分别为M、N.
求证:(1)∠BDO=∠ADO; (2)PM=PN.
学以致用
试用思维导图的方式分析此题
思维导图基本思路:要证明……只要证明……根据已知条件…… 能推出……由此得出……
解题技巧:当图形较复杂时,要学会对图形进行拆解,从复杂图形中找出简单图形再进行证明
已知:如图①,PB、PC分别是△ABC的外角平分线,PM⊥AB,PN⊥AC,垂足分别为M、N.
求证:(1)PM=PN; (2)PA平分∠MAN.
学以致用
解题技巧:题目中出现角平分线或要证明角平分线时,可作垂线段构造线段间的相等关系
知识梳理
在角的平分线上的点到这个角的两边的距离相等
角的平分线定理
角的平分线逆定理
在一个角的内部(包括顶点)且到角的两边距离相等的点,在这个角的平分线上。
方法小结:
① 解决问题时应先在头脑中建立思维导图,然后再解决问题
② 当遇到图形较复杂时,可将图形进行拆解,化复杂图形为简单图形,有利于问题的解决
③ 当题目中出现角平分线或要证明角平分线时,可作垂线段构造线段间的相等关系
④用“类比”的数学思想能解决新知识
谢谢大家
19.5角的平分线
知识链接
1、垂直平分线的定理是:
线段垂直平分线上的任意一点到这条线段两个端点的距离相等
2、垂直平分线的逆定理是:
符号语言:
符号语言:
∵AB⊥MN于O,OA=OB,∴MA=MB
和一条线段两个端点距离相等的点,在这条线段的垂直平分线上
∵MA=MB, ∴点M在线段AB的垂直平分线上
O
知识链接
4、点到直线的距离定义
过直线外一点作已知直线的垂线段,垂线段的长度叫作点到直线的距离。
3、全等三角形的判定定理
SSS SAS ASA AAS HL
创设情境
问题:现在要建一个大型超级购物中心G,使其到M城和N城的距离相等,这个超级购物中心应建于何处?
点G一定在线段MN的垂直平分线上
G
创设情境
问题:现在要建一个大型超级购物中心G,使它到两条公路的距离相等,这个超级购物中心应建于何处呢?
实验探究
按下面的过程操作:
(1)准备一块三角形纸板
(2)将其中一角对折
(3)再将开口一端对折
(过程如图所示)
(4)将折好后的纸板展开观察折痕,说出图形中的各边和各角之间的关系?
(5)变换(3)步骤中折痕的位置观察上述的结论是否有变化?
创设情境
问题:现在要建一个大型超级购物中心G,使它到两条公路的距离相等,这个超级购物中心应建于何处呢?
G
点G一定在∠AOB的角平分线上
A
O
B
(5)类比垂直平分线定理说说角平分线上的点有怎样的结论?
(6)试说出已知和求证,并用理论进行证明。
实验小结
角的平分线上的点到这个角的两边的距离相等
已知:点D在∠BAC的平分线上,DB⊥AB,DC⊥AC,
求证: DB=DC
探索新知
角平分线的定理:
在角的平分线上的点到这个角的两边的距离相等
角平分有逆定理吗?
已知:DB=DC,DB⊥AB,DC⊥AC,求证:点D在∠BAC的平分线上
角的内部,到角的两边距离相等的点在这个角的平分线上
探索新知
角平分线的逆定理:
在一个角的内部(包括顶点)且到角的两边距离相等的点,在这个角的平分线上。
角平分线的定理:
在角的平分线上的点到这个角的两边的距离相等
对比角平分的定理及其逆定理,说说他们的区别。
知识对比
角平分线的定理:
角平分线
点到直线的距离相等
角平分线的逆定理:
点到直线的距离相等
角平分线
判断下列说法是否正确?如果错误请说明原因。
①已知 OC是∠AOB的角平分线,点P是OC上一点,则PD=PE. ( )
②已知点P为∠AOB内部一点,点D在OA上,点E在OB上,若PD=PE,则OC是∠AOB的角平分线. ( )
应用角平分线定理和逆定理时,垂直条件不可少
×
×
例题分析
例1 如图,AO、BO分别是∠A、∠B的平分线,OD⊥BC,OE⊥AB,垂足分别是D、E.
求证:点O在∠C的平分线上。
F
要想证明点O在∠C的平分线上
只要证明点O到∠C的两边距离相等
已知AO是∠A的平分线OE⊥AB,OF⊥AC
OE=OF
已知BO是∠B的平分线OE⊥AB,OD⊥BC
OE=OD
OD=OF
构建点O到∠C的两边距离,过点O作OF⊥AC只要证明OD=OF
思
维
导
图
角平分线逆定理
角平分线定理
角平分线定理
等量代换
角平分线问题中常见的辅助线建立方式
解题技巧:分析几何问题时要学会先在头脑中构建思维导图
已知:如图①,点P、D在∠AOB的平分线上,OA=OB,PM⊥BD,PN⊥AD,垂足分别为M、N.
求证:(1)∠BDO=∠ADO; (2)PM=PN.
学以致用
试用思维导图的方式分析此题
思维导图基本思路:要证明……只要证明……根据已知条件…… 能推出……由此得出……
解题技巧:当图形较复杂时,要学会对图形进行拆解,从复杂图形中找出简单图形再进行证明
已知:如图①,PB、PC分别是△ABC的外角平分线,PM⊥AB,PN⊥AC,垂足分别为M、N.
求证:(1)PM=PN; (2)PA平分∠MAN.
学以致用
解题技巧:题目中出现角平分线或要证明角平分线时,可作垂线段构造线段间的相等关系
知识梳理
在角的平分线上的点到这个角的两边的距离相等
角的平分线定理
角的平分线逆定理
在一个角的内部(包括顶点)且到角的两边距离相等的点,在这个角的平分线上。
方法小结:
① 解决问题时应先在头脑中建立思维导图,然后再解决问题
② 当遇到图形较复杂时,可将图形进行拆解,化复杂图形为简单图形,有利于问题的解决
③ 当题目中出现角平分线或要证明角平分线时,可作垂线段构造线段间的相等关系
④用“类比”的数学思想能解决新知识
谢谢大家
