沪教版(上海)初中数学八年级第一学期 19.7 直角三角形全等的判定 课件(15张)
文档属性
| 名称 | 沪教版(上海)初中数学八年级第一学期 19.7 直角三角形全等的判定 课件(15张) |  | |
| 格式 | pptx | ||
| 文件大小 | 364.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-12-26 10:31:36 | ||
图片预览




文档简介
19.7 直角三角形全等的判定
如图,舞台背景的形状是两个直角三角形,工作人员想知道这两个直角三角形是否全等,但每个三角形都有一条直角边被花盆遮住无法测量.
(1)你能帮他想个办法吗?
方法一:测量斜边和一个对应的锐角. (AAS)
方法二:测量没遮住的一条直角边和一个对应的锐角. (ASA)或(AAS)
⑵ 如果他只带了一个卷尺,能完成这个任务吗?
工作人员测量了每个三角形没有被遮住的直角边和斜边,发现它们分别对应相等,于是他就肯定“两个直角三角形是全等的”.你相信他的结论吗?
下面让我们一起来验证这个结论。
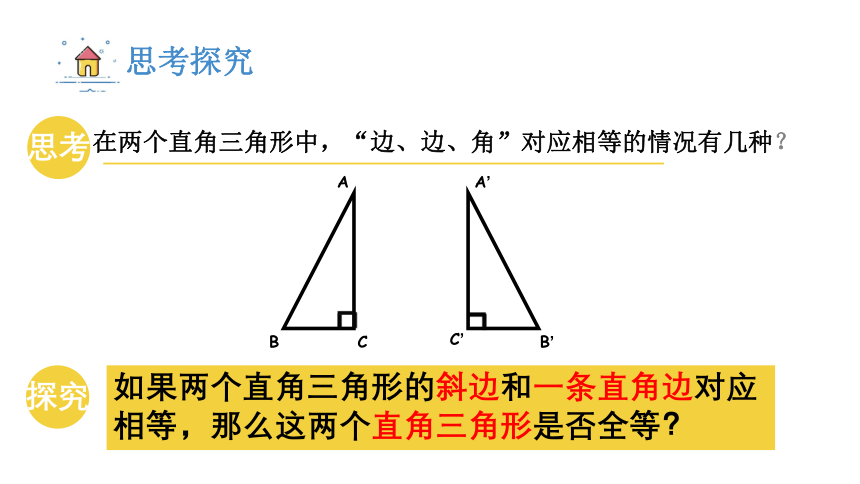
在两个直角三角形中,“边、边、角”对应相等的情况有几种?
思考
探究
思考探究
A’
C’
B’
A
B
C
如果两个直角三角形的斜边和一条直角边对应相等,那么这两个直角三角形是否全等?
探究证明
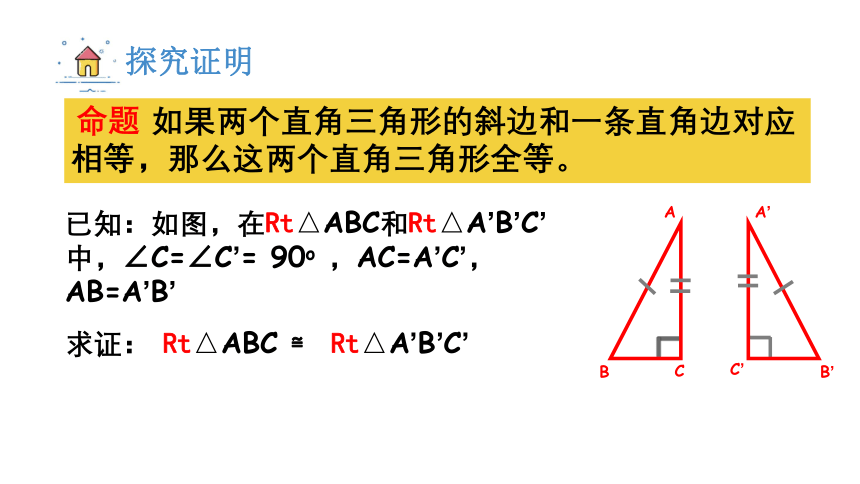
如果两个直角三角形的斜边和一条直角边对应相等,那么这两个直角三角形全等。
已知:如图,在Rt△ABC和Rt△A’B’C’中,∠C=∠C’= 90o ,AC=A’C’,AB=A’B’
求证: Rt△ABC ≌ Rt△A’B’C’
A’
C’
B’
A
B
C
命题
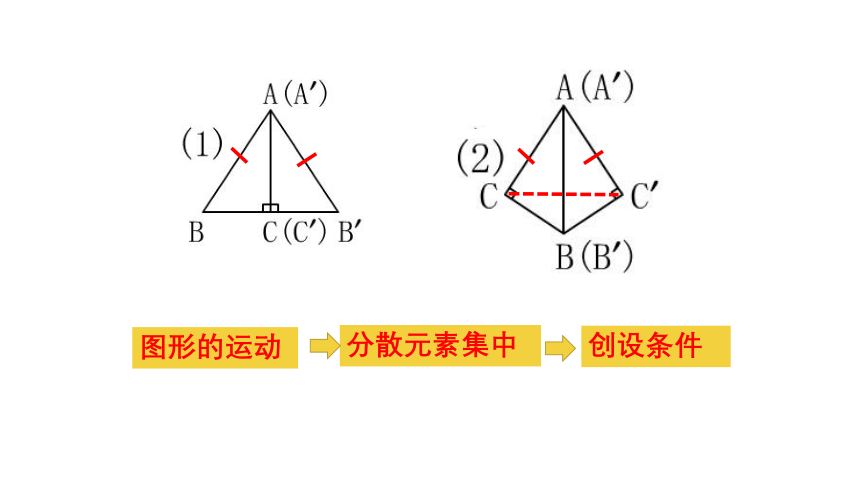
图形的运动
分散元素集中
创设条件
判定定理
如果两个直角三角形的斜边和一条直角边对应相等,那么这两个直角三角形全等。
A’
C’
B’
A
B
C
在Rt△ABC与Rt△A′B′C′中,
AB=A′B′,
AC=A′C′,
∴Rt△ABC≌Rt△A′B′C′(H.L)
(简记为H.L).
练一练
(5)AC=A’C’,AB=A’B’ ( ) _____
(4)∠A=∠A’,∠B=∠B’( ) _____
(3)AB=A’B’,BC=B’C’ ( ) _____
(2)AC=A’C’,BC=B’C’ ( ) _____
如图,具有下列条件的Rt△ABC 和Rt△A’B’C’(其中∠C=∠C’= 90o )是否全等?如果全等在( )里打“√”,并在“——”上填写判定三角形全等的理由,如果不全等,在( )里打“×”。
(1)AC=A’C’,∠A=∠A’ ( ) _____
A’
C’
B’
A
B
C
√
√
√
√
×
A.S.A.
S.A.S.
H.L.
H.L.
(6)BC=B’C’,∠A=∠A’ ( ) _____
A.A.S.
√
已知:如图,在△ABC中,BD⊥AC,CE⊥AB,点D、E为垂足,BD和CE相交于点F,BD=CE.
求证:AB=AC
B
F
E
D
A
C
例题1
联结AF,AF平分∠BAC ?为什么?
例题2
角平分线性质定理的逆定理
求证:在一个角的内部(包括顶点)且到角的两边距离相等的点,在这个角的平分线上。
已知:如图,PC⊥OA,PD⊥OB,垂足分别是点C、D,且PC=PD
求证:点P在∠AOB的平分线上
B
O
A
P
D
C
1、已知:如图,在△ABC中,AD是∠BAC的平分线,且BD=CD,DE、DF分别垂直于AB、AC,垂足分别为点E、F.
求证:EB=FC.
反馈练习
1、已知:如图,在△ABC中,AD是∠BAC的平分线,且BD=CD,DE、DF分别垂直于AB、AC,垂足分别为点E、F.
求证:EB=FC.
A
B
E
F
C
D
1、已知:如图,在△ABC中,AD是∠BAC的平分线,且BD=CD,DE、DF分别垂直于AB、AC,垂足分别为点E、F.
求证:EB=FC.
反馈练习
2、已知:如图,AD⊥CD,BC⊥CD,D、C分别为垂足,AB的垂直平分线EF交AB于点E,交CD于点F,BC=DF.
求证:AD=FC.
A
D
F
B
E
C
1、已知:如图,在△ABC中,AD是∠BAC的平分线,且BD=CD,DE、DF分别垂直于AB、AC,垂足分别E、F.
求证:EB=FC.
课堂小结
通过本节课的学习,你有什么收获、体会或想法?
1、从知识点上
2、从研究方法和思路上
“特殊” 与“一般” 关系
HL定理
图形的运动
分散元素集中
创设条件
1、已知:如图,在△ABC中,AD是∠BAC的平分线,且BD=CD,DE、DF分别垂直于AB、AC,垂足分别E、F.
求证:EB=FC.
作业
1、学习单
2、练习册19.7
谢谢 THANKS
如图,舞台背景的形状是两个直角三角形,工作人员想知道这两个直角三角形是否全等,但每个三角形都有一条直角边被花盆遮住无法测量.
(1)你能帮他想个办法吗?
方法一:测量斜边和一个对应的锐角. (AAS)
方法二:测量没遮住的一条直角边和一个对应的锐角. (ASA)或(AAS)
⑵ 如果他只带了一个卷尺,能完成这个任务吗?
工作人员测量了每个三角形没有被遮住的直角边和斜边,发现它们分别对应相等,于是他就肯定“两个直角三角形是全等的”.你相信他的结论吗?
下面让我们一起来验证这个结论。
在两个直角三角形中,“边、边、角”对应相等的情况有几种?
思考
探究
思考探究
A’
C’
B’
A
B
C
如果两个直角三角形的斜边和一条直角边对应相等,那么这两个直角三角形是否全等?
探究证明
如果两个直角三角形的斜边和一条直角边对应相等,那么这两个直角三角形全等。
已知:如图,在Rt△ABC和Rt△A’B’C’中,∠C=∠C’= 90o ,AC=A’C’,AB=A’B’
求证: Rt△ABC ≌ Rt△A’B’C’
A’
C’
B’
A
B
C
命题
图形的运动
分散元素集中
创设条件
判定定理
如果两个直角三角形的斜边和一条直角边对应相等,那么这两个直角三角形全等。
A’
C’
B’
A
B
C
在Rt△ABC与Rt△A′B′C′中,
AB=A′B′,
AC=A′C′,
∴Rt△ABC≌Rt△A′B′C′(H.L)
(简记为H.L).
练一练
(5)AC=A’C’,AB=A’B’ ( ) _____
(4)∠A=∠A’,∠B=∠B’( ) _____
(3)AB=A’B’,BC=B’C’ ( ) _____
(2)AC=A’C’,BC=B’C’ ( ) _____
如图,具有下列条件的Rt△ABC 和Rt△A’B’C’(其中∠C=∠C’= 90o )是否全等?如果全等在( )里打“√”,并在“——”上填写判定三角形全等的理由,如果不全等,在( )里打“×”。
(1)AC=A’C’,∠A=∠A’ ( ) _____
A’
C’
B’
A
B
C
√
√
√
√
×
A.S.A.
S.A.S.
H.L.
H.L.
(6)BC=B’C’,∠A=∠A’ ( ) _____
A.A.S.
√
已知:如图,在△ABC中,BD⊥AC,CE⊥AB,点D、E为垂足,BD和CE相交于点F,BD=CE.
求证:AB=AC
B
F
E
D
A
C
例题1
联结AF,AF平分∠BAC ?为什么?
例题2
角平分线性质定理的逆定理
求证:在一个角的内部(包括顶点)且到角的两边距离相等的点,在这个角的平分线上。
已知:如图,PC⊥OA,PD⊥OB,垂足分别是点C、D,且PC=PD
求证:点P在∠AOB的平分线上
B
O
A
P
D
C
1、已知:如图,在△ABC中,AD是∠BAC的平分线,且BD=CD,DE、DF分别垂直于AB、AC,垂足分别为点E、F.
求证:EB=FC.
反馈练习
1、已知:如图,在△ABC中,AD是∠BAC的平分线,且BD=CD,DE、DF分别垂直于AB、AC,垂足分别为点E、F.
求证:EB=FC.
A
B
E
F
C
D
1、已知:如图,在△ABC中,AD是∠BAC的平分线,且BD=CD,DE、DF分别垂直于AB、AC,垂足分别为点E、F.
求证:EB=FC.
反馈练习
2、已知:如图,AD⊥CD,BC⊥CD,D、C分别为垂足,AB的垂直平分线EF交AB于点E,交CD于点F,BC=DF.
求证:AD=FC.
A
D
F
B
E
C
1、已知:如图,在△ABC中,AD是∠BAC的平分线,且BD=CD,DE、DF分别垂直于AB、AC,垂足分别E、F.
求证:EB=FC.
课堂小结
通过本节课的学习,你有什么收获、体会或想法?
1、从知识点上
2、从研究方法和思路上
“特殊” 与“一般” 关系
HL定理
图形的运动
分散元素集中
创设条件
1、已知:如图,在△ABC中,AD是∠BAC的平分线,且BD=CD,DE、DF分别垂直于AB、AC,垂足分别E、F.
求证:EB=FC.
作业
1、学习单
2、练习册19.7
谢谢 THANKS
