沪教版(上海)初中数学八年级第一学期 19.7 直角三角形全等的判定 课件(15张)
文档属性
| 名称 | 沪教版(上海)初中数学八年级第一学期 19.7 直角三角形全等的判定 课件(15张) |  | |
| 格式 | ppt | ||
| 文件大小 | 489.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-12-26 10:34:48 | ||
图片预览





文档简介
19.7直角三角形全等的判定
1.一般的三角形全等的判定定理有哪些?
AAS
ASA
SAS
SSS
B
O
C
D
A
2.如图,舞台背景的形状是两个直角三角形,工作人员想知道这两个直角
三角形是否全等,但每个三角形都有一条直角边被花盆遮住无法测量.
隐藏条件:已知的直角
工作人员只带了一个卷尺,能完成任务吗?
他测量了每个三角形没有被遮住的直角边和斜边,发现它们分别对应相等,于是他就肯定“两个直角三角形是全等的”.你认为他的结论正确吗?
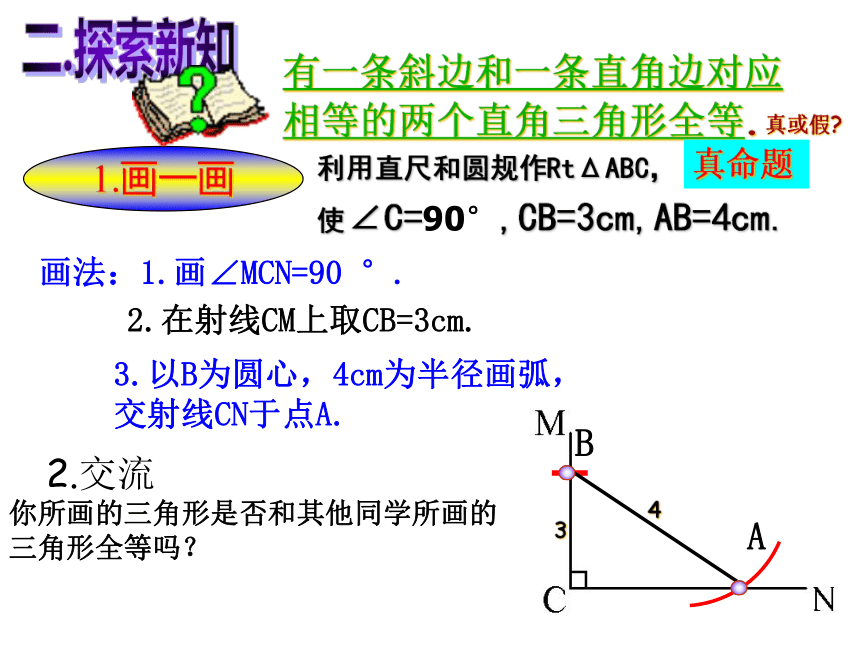
1.画一画
利用直尺和圆规作RtΔABC,
使∠C=90°,CB=3cm,AB=4cm.
B
A
有一条斜边和一条直角边对应
相等的两个直角三角形全等.
2.交流
你所画的三角形是否和其他同学所画的三角形全等吗?
3
4
画法:1.画∠MCN=90 °.
2.在射线CM上取CB=3cm.
3.以B为圆心,4cm为半径画弧,交射线CN于点A.
真命题
真或假?
B
C
A
B’
C’
A’
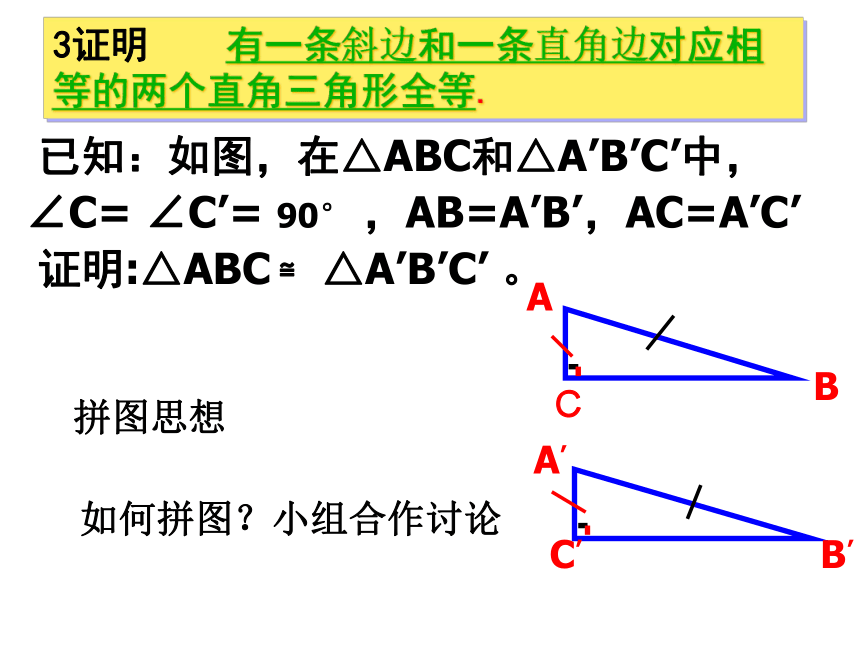
已知:如图,在△ABC和△A’B’C’中,
∠C= ∠C’= 90° ,AB=A’B’,AC=A’C’
证明:△ABC ≌ △A’B’C’ 。
3证明 有一条斜边和一条直角边对应相等的两个直角三角形全等.
拼图思想
如何拼图?小组合作讨论
证明:把△ABC和△A’B’C’ 拼在一起.因为AC=A‘C’,所以AC与A‘C’重合, B与 B‘ 在AC两侧.
C(C’)
(A‘)
B
B'
A
1
2
∵ ∠1= ∠2=90 °
∴ B,C,B‘在同一直线上,且AC ⊥BB’
∵ AB=A'B'
∴ BC=B'C'(等腰三角形三线合一)
在RtΔABC与RtΔA' B' C'中
AB=A'B'
AC=A'C'(公共边)
BC=B'C'(已证)
∴ RtΔABC ≌ RtΔA'B'C'(SSS)
简记:“斜边 (hypotenuse) 、直角边(leg)定理”或“HL”
直角三角形全等的判定方法
定理 如果两个直角三角形斜边和一条直角边对应相等,那么这两个直角三角形全等.
B
O
C
D
A
2.如图,舞台背景的形状是两个直角三角形,工作人员想知道这两个直角
三角形是否全等,但每个三角形都有一条直角边被花盆遮住无法测量.
隐藏条件:已知的直角
工作人员只带了一个卷尺,能完成任务吗?
他测量了每个三角形没有被遮住的直角边和斜边,发现它们分别对应相等,于是他就肯定“两个直角三角形是全等的”.你认为他的结论正确吗?
如图,具有下列条件的Rt△ABC和Rt△A‘B’C‘(其中
∠ C= ∠ C‘=90°)是否一定全等?说明理由。
(5)∠A= ∠ A' ,∠ B= ∠ B'
(6)AB=C'B', AC= A'C'
(ASA)
(SAS)
(AAS)
(HL)
×
×
A
B
C
A
B
C
D
E
F
1、已知: 如图,EF⊥BC于F,AD⊥BC于D,
AB=EC,EF=AD.
求证:BF=CD
∵ EF⊥BC,AD⊥BC(已知)
证明:
∴ ∠EFC= ∠ ADB=90 °(垂直的定义)
在 Rt△ABD 与 Rt△ECF 中
∴ Rt△ABD ≌ Rt△ECF(HL)
∴ BD =FC(全等三角形的对应边相等)
∴ BD-FD =CF-FD
即 BF =CD(等式性质)
AB=EC(已知)
AD=EF(已知)
A
B
C
D
E
F
2.已知:如图, AD是∠ BAC的角平分线. BD=CD , DE⊥AB,DF⊥AC,垂足分别为E,F.
求证: EB=FC
在 Rt△BED 与 Rt△CFD 中
证明:
∵ AD是∠ BAC的角平分线
DE⊥AB,DF⊥AC (已知)
∴DE=DF(角平分线上一点到角两边距离相等)
BD=CD(已知)
DE=DF(已知)
∴ Rt△BED ≌ Rt△CFD(HL)
∴ EB=FC全等三角形的对应边相等)
五.练习反馈
已知:如图,直线AC上, BE⊥AC,DF⊥AC,垂足分别为E,F, AE=CF,AB=CD .
求证: EG=FG.
直角三角形是特殊的三角形,所以不仅有一般三角形判定全等的方法(AAS,SAS,SSS,ASA),还有直角三角形特有的判定方法“HL”.
六.小 结
你能够用哪几种方法说明两个直角三角形全等?
我们应根据具体问题的实际情况选择判断两个直角三角形全等的方法.
七.作业
1)课本P114练习题1.3
2)练习册19.7
已知:如图,AD⊥CD,BC⊥CD,D、C分别为垂足,AB的垂直平分线EF交AB于点E,交CD于点F,BC=DF。
求证:AD=FC
变式:
如果将上题中”AB的垂直平分线”改为
AF ⊥FB,其他条件不变,
1). AD=FC任然成立吗?
2).探索AD,BC,DC之间有怎样的数量关系?
1.一般的三角形全等的判定定理有哪些?
AAS
ASA
SAS
SSS
B
O
C
D
A
2.如图,舞台背景的形状是两个直角三角形,工作人员想知道这两个直角
三角形是否全等,但每个三角形都有一条直角边被花盆遮住无法测量.
隐藏条件:已知的直角
工作人员只带了一个卷尺,能完成任务吗?
他测量了每个三角形没有被遮住的直角边和斜边,发现它们分别对应相等,于是他就肯定“两个直角三角形是全等的”.你认为他的结论正确吗?
1.画一画
利用直尺和圆规作RtΔABC,
使∠C=90°,CB=3cm,AB=4cm.
B
A
有一条斜边和一条直角边对应
相等的两个直角三角形全等.
2.交流
你所画的三角形是否和其他同学所画的三角形全等吗?
3
4
画法:1.画∠MCN=90 °.
2.在射线CM上取CB=3cm.
3.以B为圆心,4cm为半径画弧,交射线CN于点A.
真命题
真或假?
B
C
A
B’
C’
A’
已知:如图,在△ABC和△A’B’C’中,
∠C= ∠C’= 90° ,AB=A’B’,AC=A’C’
证明:△ABC ≌ △A’B’C’ 。
3证明 有一条斜边和一条直角边对应相等的两个直角三角形全等.
拼图思想
如何拼图?小组合作讨论
证明:把△ABC和△A’B’C’ 拼在一起.因为AC=A‘C’,所以AC与A‘C’重合, B与 B‘ 在AC两侧.
C(C’)
(A‘)
B
B'
A
1
2
∵ ∠1= ∠2=90 °
∴ B,C,B‘在同一直线上,且AC ⊥BB’
∵ AB=A'B'
∴ BC=B'C'(等腰三角形三线合一)
在RtΔABC与RtΔA' B' C'中
AB=A'B'
AC=A'C'(公共边)
BC=B'C'(已证)
∴ RtΔABC ≌ RtΔA'B'C'(SSS)
简记:“斜边 (hypotenuse) 、直角边(leg)定理”或“HL”
直角三角形全等的判定方法
定理 如果两个直角三角形斜边和一条直角边对应相等,那么这两个直角三角形全等.
B
O
C
D
A
2.如图,舞台背景的形状是两个直角三角形,工作人员想知道这两个直角
三角形是否全等,但每个三角形都有一条直角边被花盆遮住无法测量.
隐藏条件:已知的直角
工作人员只带了一个卷尺,能完成任务吗?
他测量了每个三角形没有被遮住的直角边和斜边,发现它们分别对应相等,于是他就肯定“两个直角三角形是全等的”.你认为他的结论正确吗?
如图,具有下列条件的Rt△ABC和Rt△A‘B’C‘(其中
∠ C= ∠ C‘=90°)是否一定全等?说明理由。
(5)∠A= ∠ A' ,∠ B= ∠ B'
(6)AB=C'B', AC= A'C'
(ASA)
(SAS)
(AAS)
(HL)
×
×
A
B
C
A
B
C
D
E
F
1、已知: 如图,EF⊥BC于F,AD⊥BC于D,
AB=EC,EF=AD.
求证:BF=CD
∵ EF⊥BC,AD⊥BC(已知)
证明:
∴ ∠EFC= ∠ ADB=90 °(垂直的定义)
在 Rt△ABD 与 Rt△ECF 中
∴ Rt△ABD ≌ Rt△ECF(HL)
∴ BD =FC(全等三角形的对应边相等)
∴ BD-FD =CF-FD
即 BF =CD(等式性质)
AB=EC(已知)
AD=EF(已知)
A
B
C
D
E
F
2.已知:如图, AD是∠ BAC的角平分线. BD=CD , DE⊥AB,DF⊥AC,垂足分别为E,F.
求证: EB=FC
在 Rt△BED 与 Rt△CFD 中
证明:
∵ AD是∠ BAC的角平分线
DE⊥AB,DF⊥AC (已知)
∴DE=DF(角平分线上一点到角两边距离相等)
BD=CD(已知)
DE=DF(已知)
∴ Rt△BED ≌ Rt△CFD(HL)
∴ EB=FC全等三角形的对应边相等)
五.练习反馈
已知:如图,直线AC上, BE⊥AC,DF⊥AC,垂足分别为E,F, AE=CF,AB=CD .
求证: EG=FG.
直角三角形是特殊的三角形,所以不仅有一般三角形判定全等的方法(AAS,SAS,SSS,ASA),还有直角三角形特有的判定方法“HL”.
六.小 结
你能够用哪几种方法说明两个直角三角形全等?
我们应根据具体问题的实际情况选择判断两个直角三角形全等的方法.
七.作业
1)课本P114练习题1.3
2)练习册19.7
已知:如图,AD⊥CD,BC⊥CD,D、C分别为垂足,AB的垂直平分线EF交AB于点E,交CD于点F,BC=DF。
求证:AD=FC
变式:
如果将上题中”AB的垂直平分线”改为
AF ⊥FB,其他条件不变,
1). AD=FC任然成立吗?
2).探索AD,BC,DC之间有怎样的数量关系?
