沪教版(上海)初中数学八年级第一学期 19.9 勾股定理 课件(共20张ppt)
文档属性
| 名称 | 沪教版(上海)初中数学八年级第一学期 19.9 勾股定理 课件(共20张ppt) |  | |
| 格式 | ppt | ||
| 文件大小 | 1.9MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-12-26 12:13:47 | ||
图片预览



文档简介
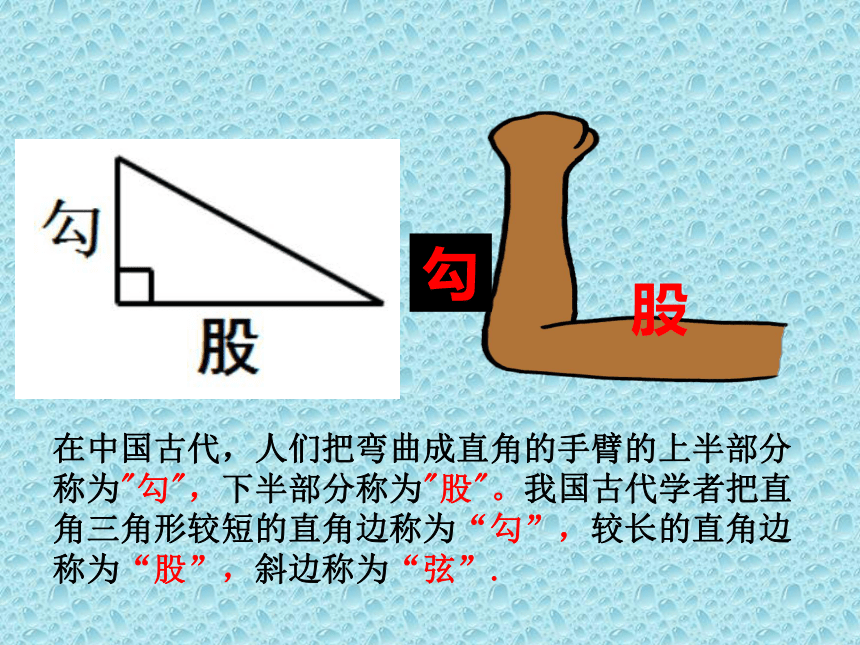
在中国古代,人们把弯曲成直角的手臂的上半部分称为"勾",下半部分称为"股"。我国古代学者把直角三角形较短的直角边称为“勾”,较长的直角边称为“股”,斜边称为“弦”.
勾
股
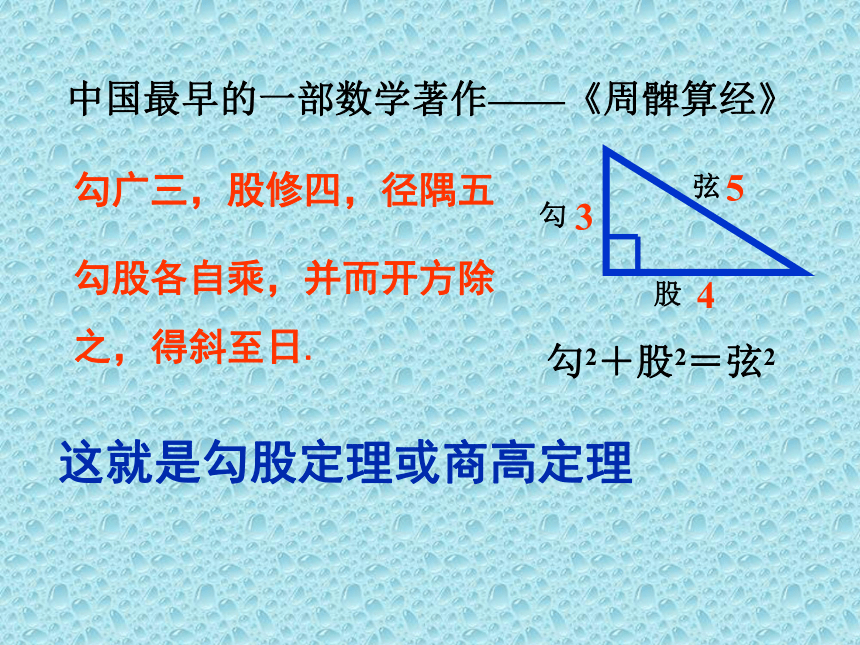
中国最早的一部数学著作——《周髀算经》
勾广三,股修四,径隅五
勾股各自乘,并而开方除
之,得斜至日.
勾2+股2=弦2
这就是勾股定理或商高定理
3
勾
股
4
弦
5
毕达哥拉斯
(公元前572----前492年),
古希腊著名的哲学家、数学家、天文学家。
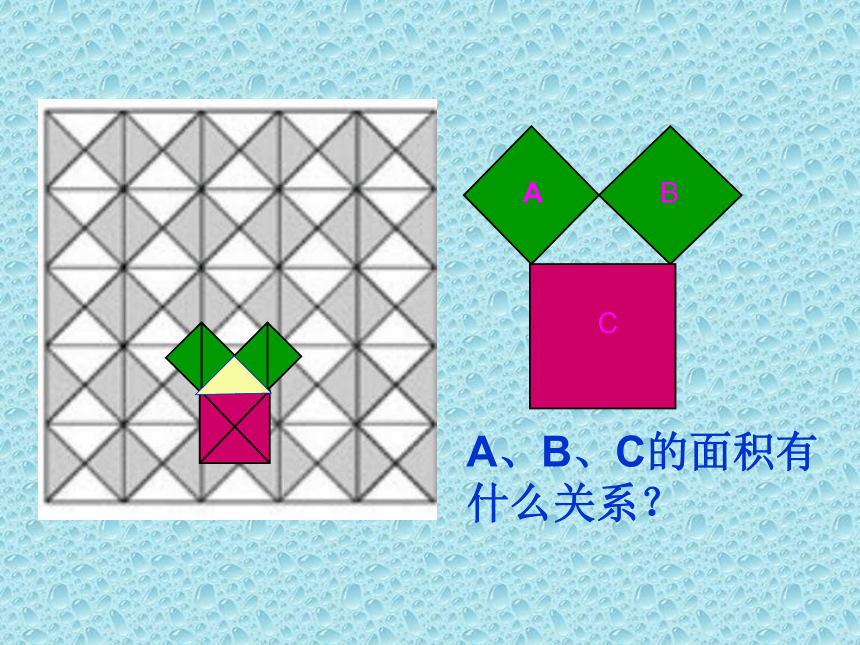
A
B
C
A、B、C的面积有
什么关系?
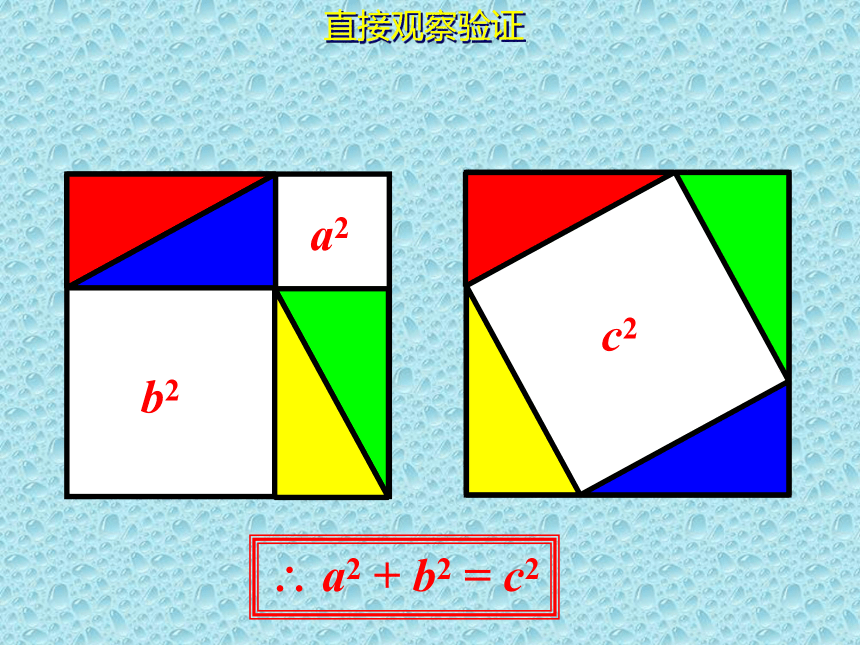
? a2 + b2 = c2
a2
b2
a2
c2
直接观察验证
a
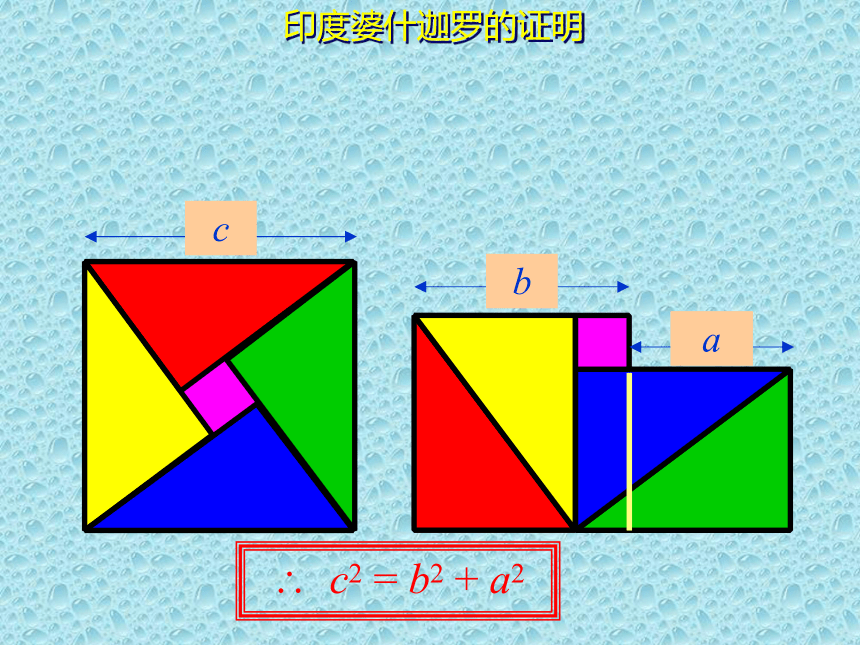
印度婆什迦罗的证明
c
? c2 = b2 + a2
b
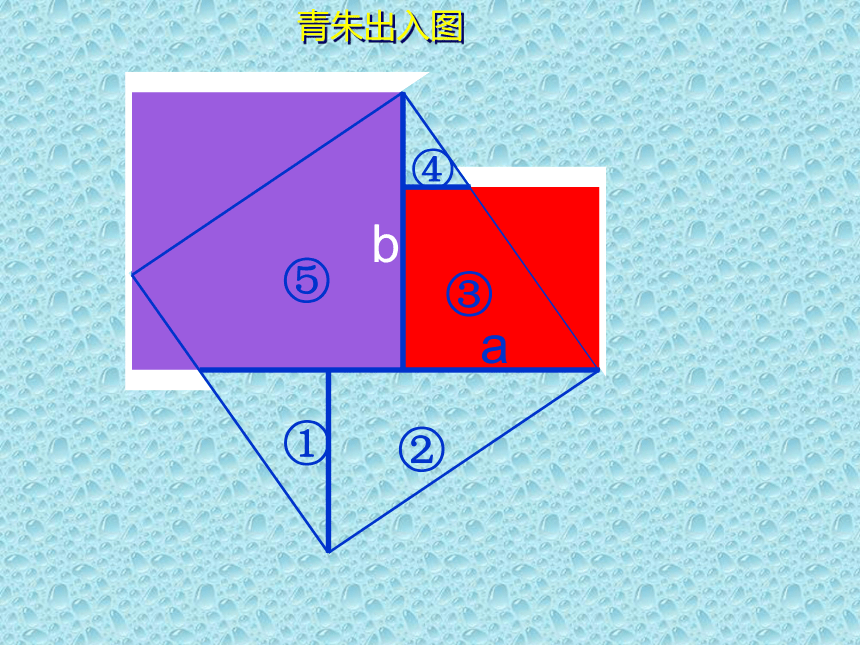
“出入相补法”
约公元 263 年,三国时代魏国的数学家刘徽为古籍
《九章算术》作注释时提出.
青出
朱方
青方
朱入
朱出
青入
青入
青出
青出
a
b
c
①
②
③
④
⑤
青朱出入图
拼图游戏
a
b
c
a
b
c
意大利著名画家达·芬奇的证法:
a
a
a
a
a
c
c
b
b
b
b
b
c
c
c
c
希腊数学家欧几里得(Euclid,公元前330~公元前275)在巨著《几何原本》给出的一种证明.
千古第一定理
数与形的第一定理
导致第一次数学危机
数学由计算转变为证明
是第一个不定方程
毕
达
哥
拉
斯
定
理
勾股(商高)定理
分别以直角三角形两条直角边为边长的两个正方形的面积之和,等于以斜边为边长的正方形的面积.
S1+S2=S3
从勾股定理到图形面积关系的拓展
分别以直角三角形两条直角边为边长的两个正三角形的面积之和,等于以斜边为边长的正三角形的面积.
S1+S2=S3
从勾股定理到图形面积关系的拓展
分别以直角三角形两条直角边为边长的两个半圆的面积之和,等于以斜边为边长的半圆的面积.
S1+S2=S3
从勾股定理到图形面积关系的拓展
勾
股
中国最早的一部数学著作——《周髀算经》
勾广三,股修四,径隅五
勾股各自乘,并而开方除
之,得斜至日.
勾2+股2=弦2
这就是勾股定理或商高定理
3
勾
股
4
弦
5
毕达哥拉斯
(公元前572----前492年),
古希腊著名的哲学家、数学家、天文学家。
A
B
C
A、B、C的面积有
什么关系?
? a2 + b2 = c2
a2
b2
a2
c2
直接观察验证
a
印度婆什迦罗的证明
c
? c2 = b2 + a2
b
“出入相补法”
约公元 263 年,三国时代魏国的数学家刘徽为古籍
《九章算术》作注释时提出.
青出
朱方
青方
朱入
朱出
青入
青入
青出
青出
a
b
c
①
②
③
④
⑤
青朱出入图
拼图游戏
a
b
c
a
b
c
意大利著名画家达·芬奇的证法:
a
a
a
a
a
c
c
b
b
b
b
b
c
c
c
c
希腊数学家欧几里得(Euclid,公元前330~公元前275)在巨著《几何原本》给出的一种证明.
千古第一定理
数与形的第一定理
导致第一次数学危机
数学由计算转变为证明
是第一个不定方程
毕
达
哥
拉
斯
定
理
勾股(商高)定理
分别以直角三角形两条直角边为边长的两个正方形的面积之和,等于以斜边为边长的正方形的面积.
S1+S2=S3
从勾股定理到图形面积关系的拓展
分别以直角三角形两条直角边为边长的两个正三角形的面积之和,等于以斜边为边长的正三角形的面积.
S1+S2=S3
从勾股定理到图形面积关系的拓展
分别以直角三角形两条直角边为边长的两个半圆的面积之和,等于以斜边为边长的半圆的面积.
S1+S2=S3
从勾股定理到图形面积关系的拓展
