沪教版(上海)初中数学八年级第一学期 19.10 两点的距离公式 课件(共13张ppt)
文档属性
| 名称 | 沪教版(上海)初中数学八年级第一学期 19.10 两点的距离公式 课件(共13张ppt) |  | |
| 格式 | pptx | ||
| 文件大小 | 850.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-12-26 12:20:17 | ||
图片预览



文档简介
19.10 两点的距离公式
A
B
A
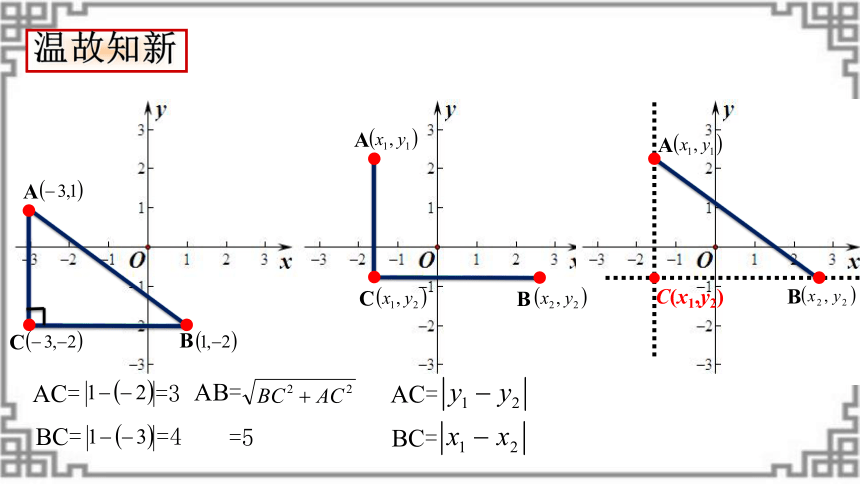
温故知新
BC=
AC=
C
B
A
B
C
C(x1,y2)
AB=
=5
BC= =4
AC= =3
B(x2,y2)
A(x1,y1)
C(x1,y2)
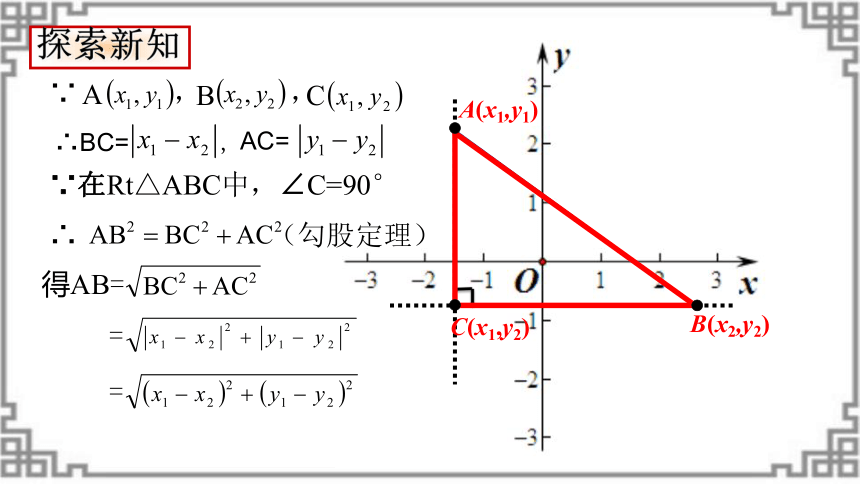
探索新知
AC=
∴BC= ,
∵ , ,
∴ (勾股定理)
得AB=
=
=
A
B
C
∵在Rt△ABC中,∠C=90°
探索新知
当A(x1,y1)、B(x2,y2)同在x轴或平行于x轴的直线上时,
AB=
当A(x1,y1)、B(x2,y2)同在y轴或平行于y轴的直线上时,
AB=
想一想:A(x1,y1)、B(x2,y2)两点同在x轴或y轴上,或者所在直线平行于坐标轴, 同样适用吗?
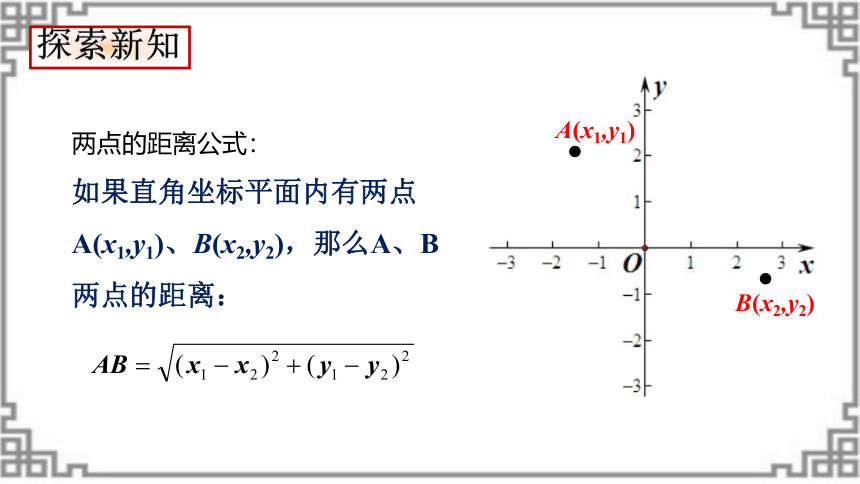
如果直角坐标平面内有两点A(x1,y1)、B(x2,y2),那么A、B两点的距离:
B(x2,y2)
A(x1,y1)
探索新知
两点的距离公式:
例题1:已知直角坐标平面内的两点分别为
A(3,3),B(6,1),求A、B两点的距离.
例题分析
小试牛刀:在直角坐标平面内,求下列两点的距离:
(1)A(2,1)、B(1,5)
(2)C(3,2)、D(-1,4)
(3)E(-5,3)、F(-3,-4)
(4)G(4,3)、H(2,3)
巩固练习
例题2:已知直角坐标平面内的△ABC三个顶点A、B、C的坐标分别为(-1,4)、(-4,-2)、(2,-5),试判断△ABC的形状.
A(-1,4)
B(-4,-2)
C(2,-5)
例题分析
例题3:已知直角坐标平面内的两点分别为A(3,3),B(6,1), 点P在 x 轴上,且PA=PB,求出点P的坐标.
例题分析
解:设点P的坐标为(m,0)
∴PA=
PB=
(两点距离公式)
∵PA=PB(已知)
∴
即
解得
∴点P的坐标是
∵A(3,3),B(6,1)(已知)
思考:已知直角坐标平面内的两点分别为A(3,3),B(6,1),
点P在坐标轴上,且PA=PB,求出点P的坐标.
巩固提升
解:①当点P在x轴上,可设点P的坐标为(m,0)
②当点P在y轴上,可设点P的坐标为(0,n)
课堂小结
通过本节课的学习,
你学到了什么?
1.必做题:练习册19.10
2.选做题:在平面直角坐标系中,O是坐标原点,已知点D的坐标为(3,4),在 x 轴正半轴上找出点P,使得△DOP为等腰三角形,求出点P的坐标.?
布置作业
谢谢同学们的合作!
A
B
A
温故知新
BC=
AC=
C
B
A
B
C
C(x1,y2)
AB=
=5
BC= =4
AC= =3
B(x2,y2)
A(x1,y1)
C(x1,y2)
探索新知
AC=
∴BC= ,
∵ , ,
∴ (勾股定理)
得AB=
=
=
A
B
C
∵在Rt△ABC中,∠C=90°
探索新知
当A(x1,y1)、B(x2,y2)同在x轴或平行于x轴的直线上时,
AB=
当A(x1,y1)、B(x2,y2)同在y轴或平行于y轴的直线上时,
AB=
想一想:A(x1,y1)、B(x2,y2)两点同在x轴或y轴上,或者所在直线平行于坐标轴, 同样适用吗?
如果直角坐标平面内有两点A(x1,y1)、B(x2,y2),那么A、B两点的距离:
B(x2,y2)
A(x1,y1)
探索新知
两点的距离公式:
例题1:已知直角坐标平面内的两点分别为
A(3,3),B(6,1),求A、B两点的距离.
例题分析
小试牛刀:在直角坐标平面内,求下列两点的距离:
(1)A(2,1)、B(1,5)
(2)C(3,2)、D(-1,4)
(3)E(-5,3)、F(-3,-4)
(4)G(4,3)、H(2,3)
巩固练习
例题2:已知直角坐标平面内的△ABC三个顶点A、B、C的坐标分别为(-1,4)、(-4,-2)、(2,-5),试判断△ABC的形状.
A(-1,4)
B(-4,-2)
C(2,-5)
例题分析
例题3:已知直角坐标平面内的两点分别为A(3,3),B(6,1), 点P在 x 轴上,且PA=PB,求出点P的坐标.
例题分析
解:设点P的坐标为(m,0)
∴PA=
PB=
(两点距离公式)
∵PA=PB(已知)
∴
即
解得
∴点P的坐标是
∵A(3,3),B(6,1)(已知)
思考:已知直角坐标平面内的两点分别为A(3,3),B(6,1),
点P在坐标轴上,且PA=PB,求出点P的坐标.
巩固提升
解:①当点P在x轴上,可设点P的坐标为(m,0)
②当点P在y轴上,可设点P的坐标为(0,n)
课堂小结
通过本节课的学习,
你学到了什么?
1.必做题:练习册19.10
2.选做题:在平面直角坐标系中,O是坐标原点,已知点D的坐标为(3,4),在 x 轴正半轴上找出点P,使得△DOP为等腰三角形,求出点P的坐标.?
布置作业
谢谢同学们的合作!
