沪教版(上海)初中数学八年级第一学期 本章小结 正比例函数、反比例函数 课件(共12张ppt)
文档属性
| 名称 | 沪教版(上海)初中数学八年级第一学期 本章小结 正比例函数、反比例函数 课件(共12张ppt) |  | |
| 格式 | ppt | ||
| 文件大小 | 719.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-12-26 12:21:14 | ||
图片预览





文档简介
1. 进一步理解正比例函数与反比例函数的定义、图像和性质;
2. 会用待定系数法求正比例函数和反比例函数的解析式;
3. 会在同一直角坐标系内求正比例函数与反比例函数的交点。
一、自学指导
1. 阅读课本P58-P71的内容,要求:
(1) 正比例函数的解析式是什么?它的图像是怎样的图形?它的有什么特殊的性质?
(2) 反比例函数的解析式是什么?它的图像是怎样的图形?它的有什么特殊的性质?
(3) 正比例函数的性质与反比例函数的性质有何异同?
4分钟后,比比完成自学检测(一)
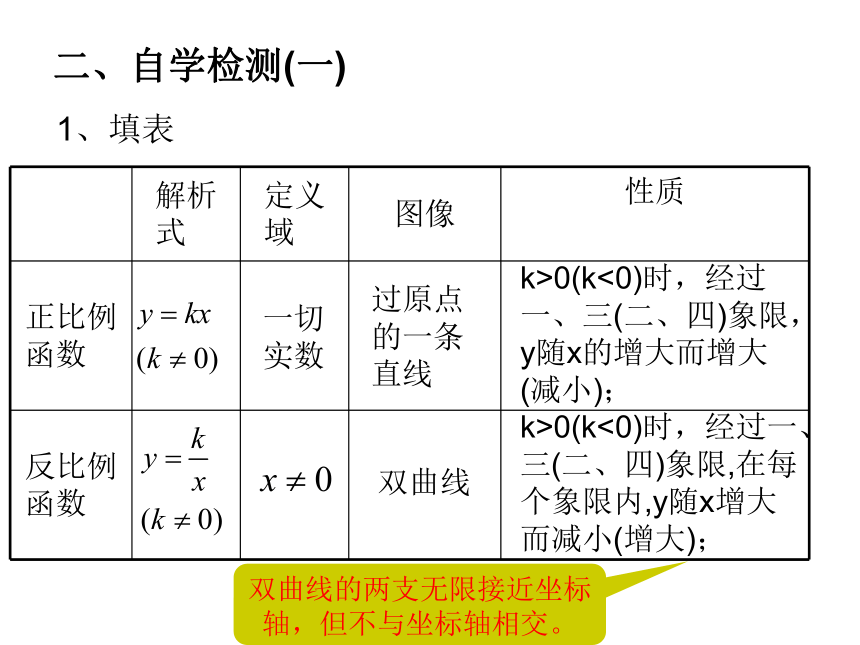
二、自学检测(一)
解析式
定义域
图像
性质
正比例函数
反比例函数
一切实数
过原点的一条直线
双曲线
k>0(k<0)时,经过一、三(二、四)象限,y随x的增大而增大(减小);
k>0(k<0)时,经过一、三(二、四)象限,在每个象限内,y随x增大而减小(增大);
1、填表
双曲线的两支无限接近坐标轴,但不与坐标轴相交。
2、下列函数中,哪些是正比例函数?
哪些是反比例函数?
(1) (2) (3)
(4) (5) (6)
3、(1) 函数y=3x的图象经过原点且在第_______象限内,y随x的增大而_____.
(2) 函数 的图象的两个分支在第_______象限内,在每个象限内, y随x的增大而________。
4、已知y与x成正比例,且当x=2时,y=-4,则y与x的函数解析式是______。
5、已知反比例函数的图像经过点P(1.5,-2),则反比例函数的解析式是_____。
一、三
增大
二、四
增大
6、正比例函数y=kx和反比例函数 的图像交于M、N两点,且点M的横坐标为-2,请求出正比例函数的解析式和两交点M、N的坐标。
解:∵M点横坐标为-2
∴设M(-2,b)
又∵反比例函数经过点M
∴b=3,得M(-2,3)
∵正比例函数y=kx经过点M
∴3=-2k
得:k=-1.5
∴y=-1.5x
解得:
∴N(2,-3)
1、如图1,在Rt△AOB的面积为3,点A在双曲线的第四象限内的分支上,且AB⊥x轴,求这个反比例函数的解析式。
2、如图2,点P是反比例函数 图像上一点,PA⊥y轴,A(0,4),AP=2。
(1) 求反比例函数解析式;
(2) 求直线OP的解析式。
A
B
O
x
y
图1
y
P
O
A
图2
x
点P坐标(-2,4)
反比例函数解析式:
正比例函数解析式:
3、已知 ,y1与x成正比例,y2与x-2成反比例,且当x=1时,y=3;x=3时,y=1,求y与x的函数解析式。
解:设
解析式
定义域
图像
性质
正比例函数
反比例函数
一切实数
过原点的一条直线
双曲线
k>0(k<0)时,经过一、三(二、四)象限,y随x的增大而增大(减小);
k>0(k<0)时,经过一、三(二、四)象限,在每个象限内,y随x增大而减小(增大);
1、正比例函数、反比例函数的解析式、图像、性质
2、会用待定系数法求函数解析式
3、求两个函数的交点坐标即求这两个函数解析式所组成的方程组的解。
四、当堂训练
1、下列结论正确的是( )
A. 函数 中,y随x的增大而减小;
B. 函数 中,y随x的增大而减小;
C. 函数 中,y随x的增大而减小;
D. 函数 中,y随x的增大而增大。
2、已知 图像上一点到y轴的距离是 ,求这个点的坐标。
3、若正比例函数 和反比例函数 的比例系数互为倒数,且反比例函数的图像经过点(2,-1),求正比例函数的解析式;并求它们的交点坐标。
4、如图,已知正比例函数 与反比例函数
的图像的交点为A、B,其中点B的纵坐标为-1,过点A作x轴的垂线与过点B作y轴的垂线交于点P,求反比例函数的解析式、点P的坐标和△ABP的面积。
y
x
O
A
B
P
2. 会用待定系数法求正比例函数和反比例函数的解析式;
3. 会在同一直角坐标系内求正比例函数与反比例函数的交点。
一、自学指导
1. 阅读课本P58-P71的内容,要求:
(1) 正比例函数的解析式是什么?它的图像是怎样的图形?它的有什么特殊的性质?
(2) 反比例函数的解析式是什么?它的图像是怎样的图形?它的有什么特殊的性质?
(3) 正比例函数的性质与反比例函数的性质有何异同?
4分钟后,比比完成自学检测(一)
二、自学检测(一)
解析式
定义域
图像
性质
正比例函数
反比例函数
一切实数
过原点的一条直线
双曲线
k>0(k<0)时,经过一、三(二、四)象限,y随x的增大而增大(减小);
k>0(k<0)时,经过一、三(二、四)象限,在每个象限内,y随x增大而减小(增大);
1、填表
双曲线的两支无限接近坐标轴,但不与坐标轴相交。
2、下列函数中,哪些是正比例函数?
哪些是反比例函数?
(1) (2) (3)
(4) (5) (6)
3、(1) 函数y=3x的图象经过原点且在第_______象限内,y随x的增大而_____.
(2) 函数 的图象的两个分支在第_______象限内,在每个象限内, y随x的增大而________。
4、已知y与x成正比例,且当x=2时,y=-4,则y与x的函数解析式是______。
5、已知反比例函数的图像经过点P(1.5,-2),则反比例函数的解析式是_____。
一、三
增大
二、四
增大
6、正比例函数y=kx和反比例函数 的图像交于M、N两点,且点M的横坐标为-2,请求出正比例函数的解析式和两交点M、N的坐标。
解:∵M点横坐标为-2
∴设M(-2,b)
又∵反比例函数经过点M
∴b=3,得M(-2,3)
∵正比例函数y=kx经过点M
∴3=-2k
得:k=-1.5
∴y=-1.5x
解得:
∴N(2,-3)
1、如图1,在Rt△AOB的面积为3,点A在双曲线的第四象限内的分支上,且AB⊥x轴,求这个反比例函数的解析式。
2、如图2,点P是反比例函数 图像上一点,PA⊥y轴,A(0,4),AP=2。
(1) 求反比例函数解析式;
(2) 求直线OP的解析式。
A
B
O
x
y
图1
y
P
O
A
图2
x
点P坐标(-2,4)
反比例函数解析式:
正比例函数解析式:
3、已知 ,y1与x成正比例,y2与x-2成反比例,且当x=1时,y=3;x=3时,y=1,求y与x的函数解析式。
解:设
解析式
定义域
图像
性质
正比例函数
反比例函数
一切实数
过原点的一条直线
双曲线
k>0(k<0)时,经过一、三(二、四)象限,y随x的增大而增大(减小);
k>0(k<0)时,经过一、三(二、四)象限,在每个象限内,y随x增大而减小(增大);
1、正比例函数、反比例函数的解析式、图像、性质
2、会用待定系数法求函数解析式
3、求两个函数的交点坐标即求这两个函数解析式所组成的方程组的解。
四、当堂训练
1、下列结论正确的是( )
A. 函数 中,y随x的增大而减小;
B. 函数 中,y随x的增大而减小;
C. 函数 中,y随x的增大而减小;
D. 函数 中,y随x的增大而增大。
2、已知 图像上一点到y轴的距离是 ,求这个点的坐标。
3、若正比例函数 和反比例函数 的比例系数互为倒数,且反比例函数的图像经过点(2,-1),求正比例函数的解析式;并求它们的交点坐标。
4、如图,已知正比例函数 与反比例函数
的图像的交点为A、B,其中点B的纵坐标为-1,过点A作x轴的垂线与过点B作y轴的垂线交于点P,求反比例函数的解析式、点P的坐标和△ABP的面积。
y
x
O
A
B
P
