沪教版(上海)初中数学八年级第一学期19.2(1)证明举例 课件(共16张ppt)
文档属性
| 名称 | 沪教版(上海)初中数学八年级第一学期19.2(1)证明举例 课件(共16张ppt) |

|
|
| 格式 | ppt | ||
| 文件大小 | 422.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-12-26 00:00:00 | ||
图片预览




文档简介
1、平行线的性质:
①∵ AC∥EF (已知),
∴∠A=∠1( )
②∵AC∥EF (已知),
∴∠2=∠3( )
③∵AC∥EF (已知),
∴ ∠3+∠4=180°( )
两直线平行, 内错角相等
两直线平行, 同位角相等
两直线平行, 同旁内角互补
2、平行线的判定方法:
①∵∠A=∠2(已知),
∴AB∥DF( )
②∵∠1=∠3(已知),
∴AB∥DF ( )
③∵∠A+∠4=180°(已知),
∴AB∥DF ( )
④∵a∥b, b∥c(已知),
∴a∥c( )
同位角相等,两直线平行
内错角相等,两直线平行
同旁内角互补,两直线平行
平行于同一直线的两直线平行
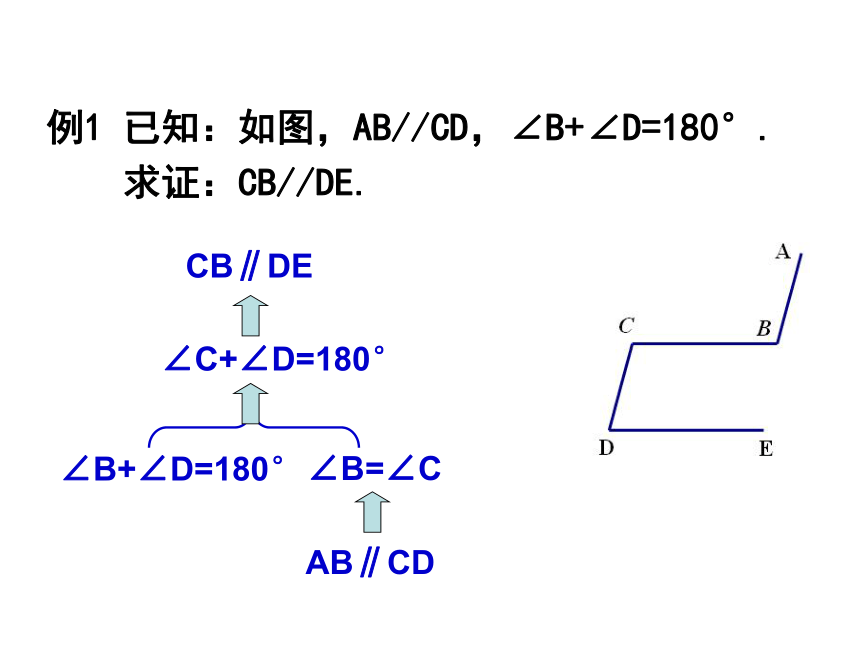
例1 已知:如图,AB//CD,∠B+∠D=180°.
求证:CB//DE.
AB∥CD
∠B=∠C
∠B+∠D=180°
∠C+∠D=180°
CB∥DE
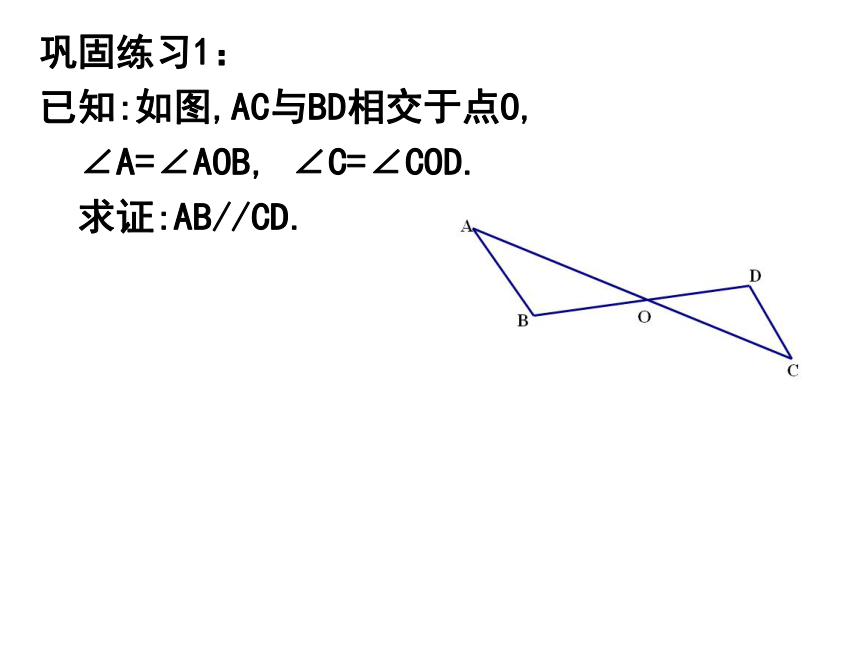
巩固练习1:
已知:如图,AC与BD相交于点O,
∠A=∠AOB, ∠C=∠COD.
求证:AB//CD.
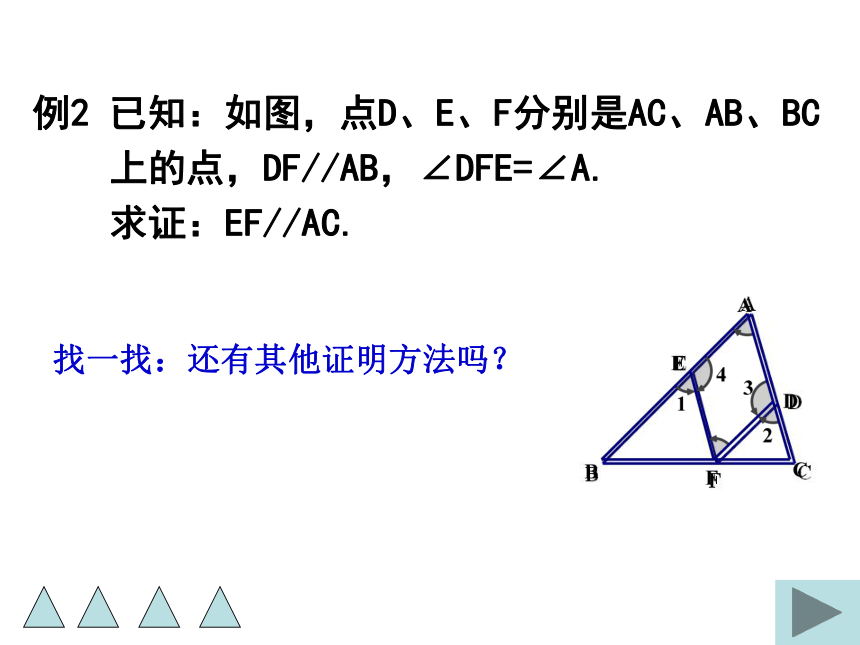
例2 已知:如图,点D、E、F分别是AC、AB、BC
上的点,DF//AB,∠DFE=∠A.
求证:EF//AC.
找一找:还有其他证明方法吗?
证明:∵DF//AB(已知),
∴ ∠1=∠DFE(两直线平行,内错角相等).
又∵∠DFE=∠A(已知),
∴ ∠1=∠A(等量代换).
∴EF//AC(同位角相等,两直线平行).
证明:∵DF//AB(已知),
∴ ∠2=∠A(两直线平行,同位角相等).
又∵∠DFE=∠A(已知),
∴ ∠2=∠DFE(等量代换).
∴EF//AC(内错角相等,两直线平行).
证明:∵DF//AB(已知),
∴ ∠A+ ∠3=180? (两直线平行,同旁内角互补).
又∵∠DFE=∠A(已知),
∴ ∠DFE+ ∠3=180? (等量代换).
∴EF//AC(同旁内角互补,两直线平行).
证明:∵DF//AB(已知),
∴ ∠DFE+ ∠4=180? (两直线平行,同旁内角互补).
又∵∠DFE=∠A(已知),
∴ ∠A+ ∠4=180? (等量代换).
∴EF//AC(同旁内角互补,两直线平行).
例3 如图,已知OA=OD,∠1=∠2, 求证:AD//BC.
证明:∵∠1=∠2(已知)
又∠1+∠2+∠BOC=180°(三角形内角和为180°)
2∠1+∠BOC=180°(等量代换)
∴∠1= (180°-∠BOC)(等式性质)
又 ∵OA=OD(已知)
∴∠3=∠4(等边对等角)
同理: ∠4= (180°-∠AOD)
又∵∠AOD=∠BOC(对顶角相等)
∴∠1= ∠4(等量代换)
∴ AD∥BC(内错角相等,两直线平行)
3
4
巩固练习2:
已知:如图,点D、E分别在△ABC的边AB、AC上,AB=AC.
(1)如果DE//BC,求证:AD=AE.
(2)如果AD=AE,求证:DE//BC.
谈谈你对这节课的体会和收获?
五、提升能力:
如图,四边形ABCD中,DE平分∠ADC,交AB于点E,∠GBC=∠BGC,BG//ED交AD延长线于P,求证:AD//BC.
六、作业布置:
1、练习19.2(1)
2、补充练习:(选做)
A组:(基础题)
1、已知:如图,AB=AD,DB平分∠ABC,求证:AD//BC.
2、如图,已知AC//DE,∠1=∠2,求证:AB//CD.
3、如图,已知AB//CD,∠1=∠2,求证:EB//CF.
B组:(中等题)
4、已知:如图,∠A=∠F,∠C=∠D,求证:BD//CE.
5、如图,已知∠1=∠A, ∠B=∠D,求证:BC//DF.
C组:(提高题)
6、如图,已知AD⊥BC,EF⊥BC, ∠1=∠2,求证:DG//BA.
①∵ AC∥EF (已知),
∴∠A=∠1( )
②∵AC∥EF (已知),
∴∠2=∠3( )
③∵AC∥EF (已知),
∴ ∠3+∠4=180°( )
两直线平行, 内错角相等
两直线平行, 同位角相等
两直线平行, 同旁内角互补
2、平行线的判定方法:
①∵∠A=∠2(已知),
∴AB∥DF( )
②∵∠1=∠3(已知),
∴AB∥DF ( )
③∵∠A+∠4=180°(已知),
∴AB∥DF ( )
④∵a∥b, b∥c(已知),
∴a∥c( )
同位角相等,两直线平行
内错角相等,两直线平行
同旁内角互补,两直线平行
平行于同一直线的两直线平行
例1 已知:如图,AB//CD,∠B+∠D=180°.
求证:CB//DE.
AB∥CD
∠B=∠C
∠B+∠D=180°
∠C+∠D=180°
CB∥DE
巩固练习1:
已知:如图,AC与BD相交于点O,
∠A=∠AOB, ∠C=∠COD.
求证:AB//CD.
例2 已知:如图,点D、E、F分别是AC、AB、BC
上的点,DF//AB,∠DFE=∠A.
求证:EF//AC.
找一找:还有其他证明方法吗?
证明:∵DF//AB(已知),
∴ ∠1=∠DFE(两直线平行,内错角相等).
又∵∠DFE=∠A(已知),
∴ ∠1=∠A(等量代换).
∴EF//AC(同位角相等,两直线平行).
证明:∵DF//AB(已知),
∴ ∠2=∠A(两直线平行,同位角相等).
又∵∠DFE=∠A(已知),
∴ ∠2=∠DFE(等量代换).
∴EF//AC(内错角相等,两直线平行).
证明:∵DF//AB(已知),
∴ ∠A+ ∠3=180? (两直线平行,同旁内角互补).
又∵∠DFE=∠A(已知),
∴ ∠DFE+ ∠3=180? (等量代换).
∴EF//AC(同旁内角互补,两直线平行).
证明:∵DF//AB(已知),
∴ ∠DFE+ ∠4=180? (两直线平行,同旁内角互补).
又∵∠DFE=∠A(已知),
∴ ∠A+ ∠4=180? (等量代换).
∴EF//AC(同旁内角互补,两直线平行).
例3 如图,已知OA=OD,∠1=∠2, 求证:AD//BC.
证明:∵∠1=∠2(已知)
又∠1+∠2+∠BOC=180°(三角形内角和为180°)
2∠1+∠BOC=180°(等量代换)
∴∠1= (180°-∠BOC)(等式性质)
又 ∵OA=OD(已知)
∴∠3=∠4(等边对等角)
同理: ∠4= (180°-∠AOD)
又∵∠AOD=∠BOC(对顶角相等)
∴∠1= ∠4(等量代换)
∴ AD∥BC(内错角相等,两直线平行)
3
4
巩固练习2:
已知:如图,点D、E分别在△ABC的边AB、AC上,AB=AC.
(1)如果DE//BC,求证:AD=AE.
(2)如果AD=AE,求证:DE//BC.
谈谈你对这节课的体会和收获?
五、提升能力:
如图,四边形ABCD中,DE平分∠ADC,交AB于点E,∠GBC=∠BGC,BG//ED交AD延长线于P,求证:AD//BC.
六、作业布置:
1、练习19.2(1)
2、补充练习:(选做)
A组:(基础题)
1、已知:如图,AB=AD,DB平分∠ABC,求证:AD//BC.
2、如图,已知AC//DE,∠1=∠2,求证:AB//CD.
3、如图,已知AB//CD,∠1=∠2,求证:EB//CF.
B组:(中等题)
4、已知:如图,∠A=∠F,∠C=∠D,求证:BD//CE.
5、如图,已知∠1=∠A, ∠B=∠D,求证:BC//DF.
C组:(提高题)
6、如图,已知AD⊥BC,EF⊥BC, ∠1=∠2,求证:DG//BA.
