沪教版(上海)数学八年级第二学期22.2(3)平行四边形的判定 课件(15张)
文档属性
| 名称 | 沪教版(上海)数学八年级第二学期22.2(3)平行四边形的判定 课件(15张) |

|
|
| 格式 | pptx | ||
| 文件大小 | 139.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-12-26 00:00:00 | ||
图片预览



文档简介
22.2(3)平行四边形的判定
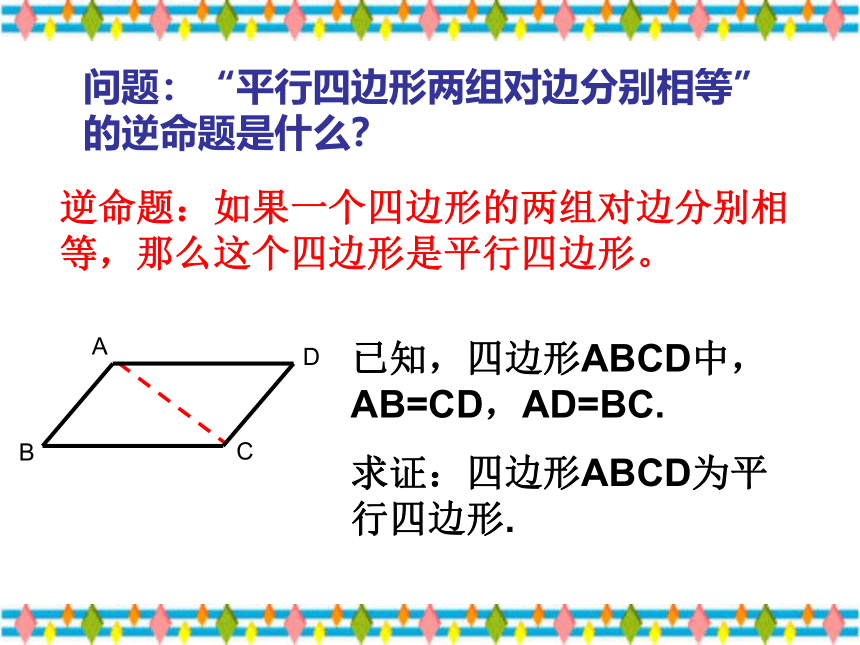
已知,四边形ABCD中,AB=CD,AD=BC.
求证:四边形ABCD为平行四边形.
问题:“平行四边形两组对边分别相等”的逆命题是什么?
A
D
C
B
逆命题:如果一个四边形的两组对边分别相等,那么这个四边形是平行四边形。
B
D
A
C
已知:四边形ABCD,
AB=CD,AD=BC
求证:四边形ABCD是平行四边形
2
1
3
4
证明:
∴∠1=∠2,∠3=∠4(全等三角形的对应角相等)
∴
AB∥CD,AD∥BC
(内错角相等,两直线平行)
∴四边形ABCD是平行四边形(平行四边形的定义)
联结AC
∵
在∴△ABC和△CDA中,
AB=CD(已知)
AD=BC
(已知)
AC=AC
(公共边)
∴△ABC≌△CDA(SSS)
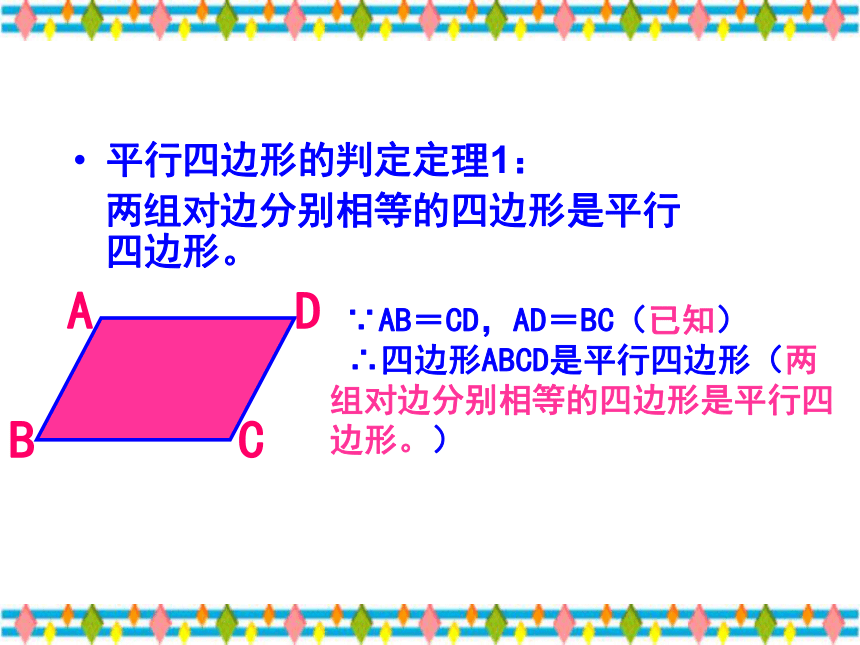
平行四边形的判定定理1:
两组对边分别相等的四边形是平行四边形。
A
B
C
D
∵AB=CD,AD=BC(已知)
∴四边形ABCD是平行四边形(两
组对边分别相等的四边形是平行四边形。)
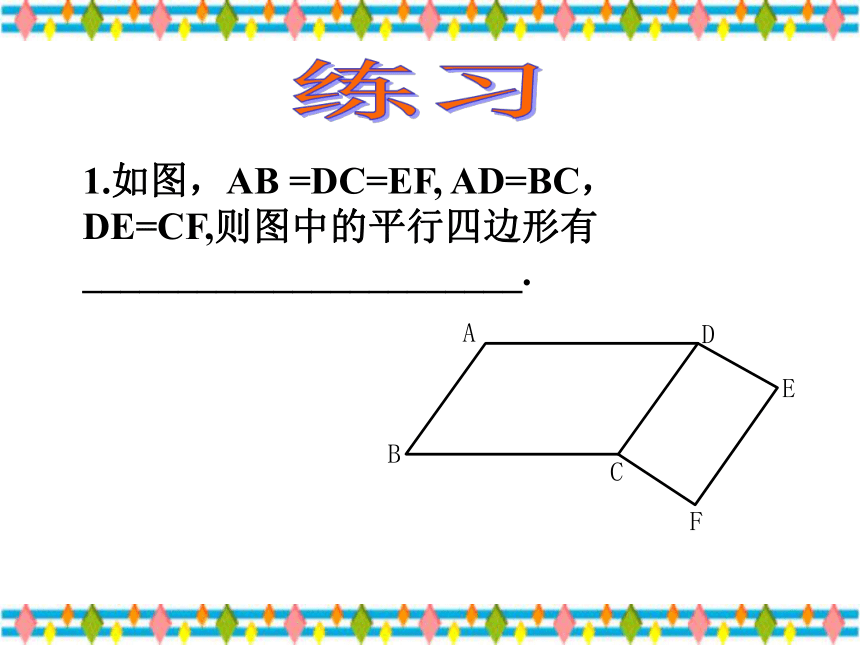
1.如图,AB
=DC=EF,
AD=BC,DE=CF,则图中的平行四边形有_______________________.
练习
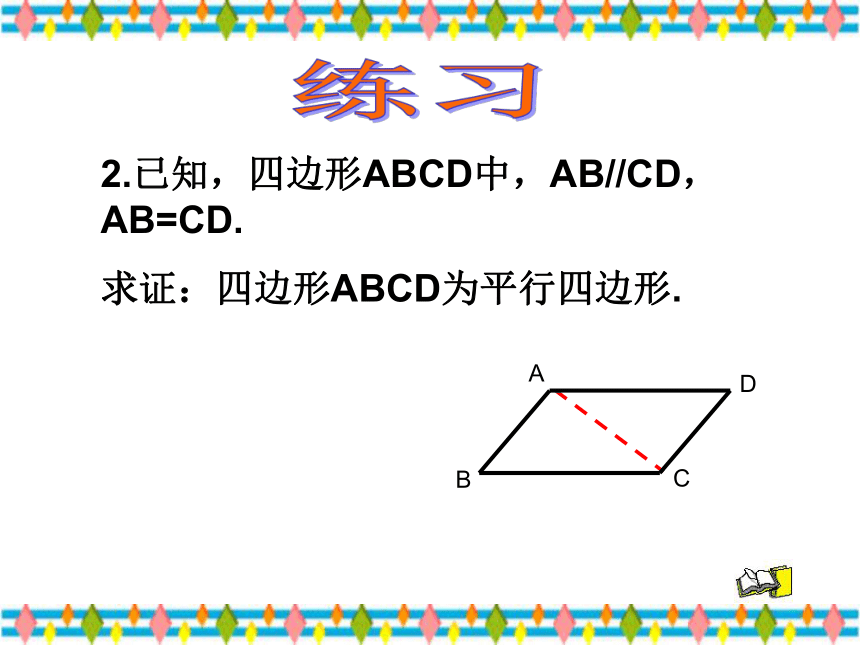
2.已知,四边形ABCD中,AB//CD,AB=CD.
求证:四边形ABCD为平行四边形.
A
D
C
B
练行四边形的判定定理2:
一组对边平行且相等的四边形是平行四边形。
A
B
C
D
∵
AB=CD,
AB∥CD
(已知)
∴四边形ABCD是平行四边形(一组对边平行且相等的四边形是平行四边形。)
3.已知:①AB//CD
②AB=CD
③BC//AD
④BC=AD,满足哪两个条件,四边形ABCD为平行四边形,下列选法错误的是(
)
(A)①③
(B)②④
(C)①②
(D)①④
练习
如图,?ABCD中,E,F分别在边BC,AD上,且BE=DF;
求证:四边形AECF是平行四边形.
例题选讲
1.已知:如图,平行四边形ABCD中,E、F分别是边AB和CD的中点.
求证:EF=BC
试一试
试一试
2.如图,?ABCD中,E、F、G、H分别是BC、
AD、AB、CD的中点,
求证:四边形EFGH是平行四边形.
小结
本节课,我们学习了哪些内容?
平行四边形的判定方法:
1.平行四边形的判定定理:
1.)两组对边分别相等的四边形是平行四边形
2.)一组对边平行且相等的四边形是平行四边形
2.两组对边分别平行的四边形是平行四边形(定义)
拓展练习:
在四边形ABCD
中,AD∥BC,且AD
>BC,BC
=
6cm,P,Q
分别从A,C
同时出发,P
以1厘米/秒的速度由A
向D
运动,Q
以2厘米/秒的速度由C
向B
运动,几秒后四边形ABQP
成为平行四边形?
作业:
练习册
第38页
习题22.2(3)
已知,四边形ABCD中,AB=CD,AD=BC.
求证:四边形ABCD为平行四边形.
问题:“平行四边形两组对边分别相等”的逆命题是什么?
A
D
C
B
逆命题:如果一个四边形的两组对边分别相等,那么这个四边形是平行四边形。
B
D
A
C
已知:四边形ABCD,
AB=CD,AD=BC
求证:四边形ABCD是平行四边形
2
1
3
4
证明:
∴∠1=∠2,∠3=∠4(全等三角形的对应角相等)
∴
AB∥CD,AD∥BC
(内错角相等,两直线平行)
∴四边形ABCD是平行四边形(平行四边形的定义)
联结AC
∵
在∴△ABC和△CDA中,
AB=CD(已知)
AD=BC
(已知)
AC=AC
(公共边)
∴△ABC≌△CDA(SSS)
平行四边形的判定定理1:
两组对边分别相等的四边形是平行四边形。
A
B
C
D
∵AB=CD,AD=BC(已知)
∴四边形ABCD是平行四边形(两
组对边分别相等的四边形是平行四边形。)
1.如图,AB
=DC=EF,
AD=BC,DE=CF,则图中的平行四边形有_______________________.
练习
2.已知,四边形ABCD中,AB//CD,AB=CD.
求证:四边形ABCD为平行四边形.
A
D
C
B
练行四边形的判定定理2:
一组对边平行且相等的四边形是平行四边形。
A
B
C
D
∵
AB=CD,
AB∥CD
(已知)
∴四边形ABCD是平行四边形(一组对边平行且相等的四边形是平行四边形。)
3.已知:①AB//CD
②AB=CD
③BC//AD
④BC=AD,满足哪两个条件,四边形ABCD为平行四边形,下列选法错误的是(
)
(A)①③
(B)②④
(C)①②
(D)①④
练习
如图,?ABCD中,E,F分别在边BC,AD上,且BE=DF;
求证:四边形AECF是平行四边形.
例题选讲
1.已知:如图,平行四边形ABCD中,E、F分别是边AB和CD的中点.
求证:EF=BC
试一试
试一试
2.如图,?ABCD中,E、F、G、H分别是BC、
AD、AB、CD的中点,
求证:四边形EFGH是平行四边形.
小结
本节课,我们学习了哪些内容?
平行四边形的判定方法:
1.平行四边形的判定定理:
1.)两组对边分别相等的四边形是平行四边形
2.)一组对边平行且相等的四边形是平行四边形
2.两组对边分别平行的四边形是平行四边形(定义)
拓展练习:
在四边形ABCD
中,AD∥BC,且AD
>BC,BC
=
6cm,P,Q
分别从A,C
同时出发,P
以1厘米/秒的速度由A
向D
运动,Q
以2厘米/秒的速度由C
向B
运动,几秒后四边形ABQP
成为平行四边形?
作业:
练习册
第38页
习题22.2(3)
