华东师大版七年级上册5.1.3 同位角内错角同旁内角 课件(23张)
文档属性
| 名称 | 华东师大版七年级上册5.1.3 同位角内错角同旁内角 课件(23张) |
|
|
| 格式 | ppt | ||
| 文件大小 | 1.5MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-12-26 00:00:00 | ||
图片预览





文档简介
C
D
E
F
1
3
4
2
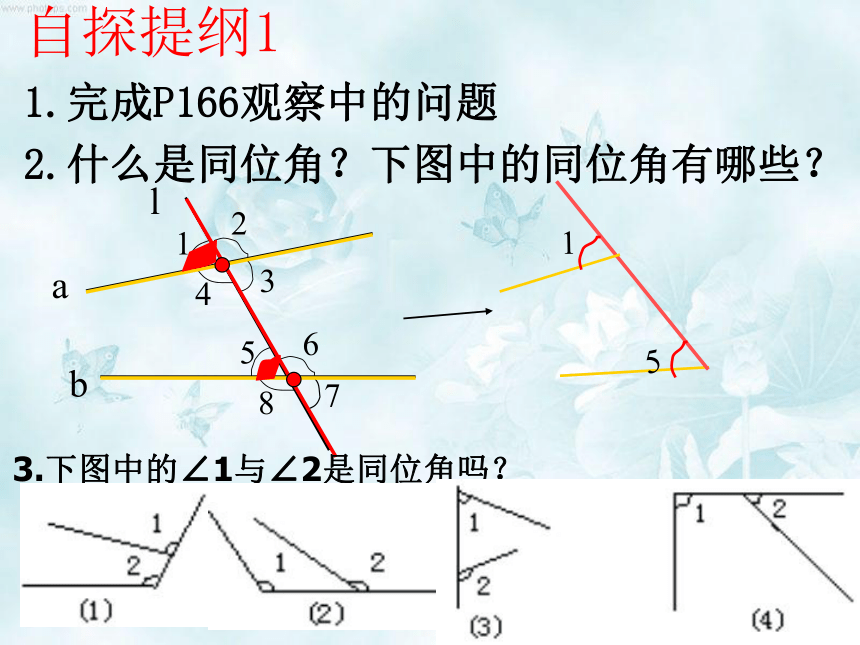
两条直线CD和EF相交,构成几个角?他们之间是什么位置关系的角?
A
C
B
D
E
F
若再添加一条直线,怎样描述这三条直线的位置关系?构成几个角?
两条直线AB、CD被
第三条直线EF所截
7
1
2
3
4
5
6
8
截线
被截直线
学习目标
1.理解同位角、内错角、同旁内角的概念。
2.能从图形中找出同位角、内错角、同旁
内角。
设疑自探
同学们,根据本节课题结合学习目标,你有那些问题,请提出来。
1.理解同位角、内错角、同旁内角的概念。
2.能从图形中找出同位角、内错角、同旁
内角。
自探提纲1
1.完成P166观察中的问题
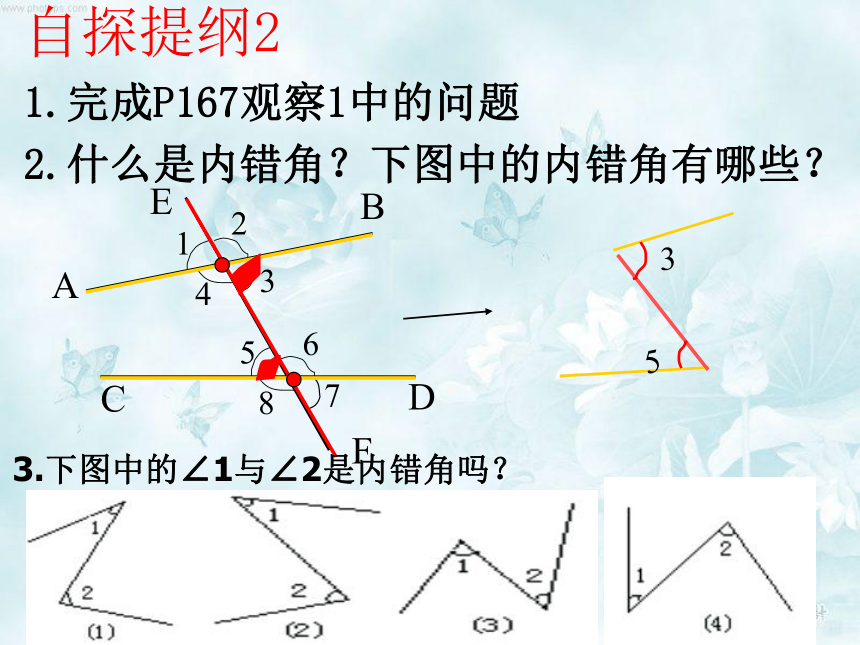
2.什么是同位角?下图中的同位角有哪些?
a
b
l
2
1
4
3
6
5
8
7
1
5
3.下图中的∠1与∠2是同位角吗?
自探提纲2
1.完成P167观察1中的问题
2.什么是内错角?下图中的内错角有哪些?
A
C
B
D
E
2
1
4
3
6
5
8
7
3
5
F
3.下图中的∠1与∠2是内错角吗?
自探提纲3
1.完成P167观察2中的问题
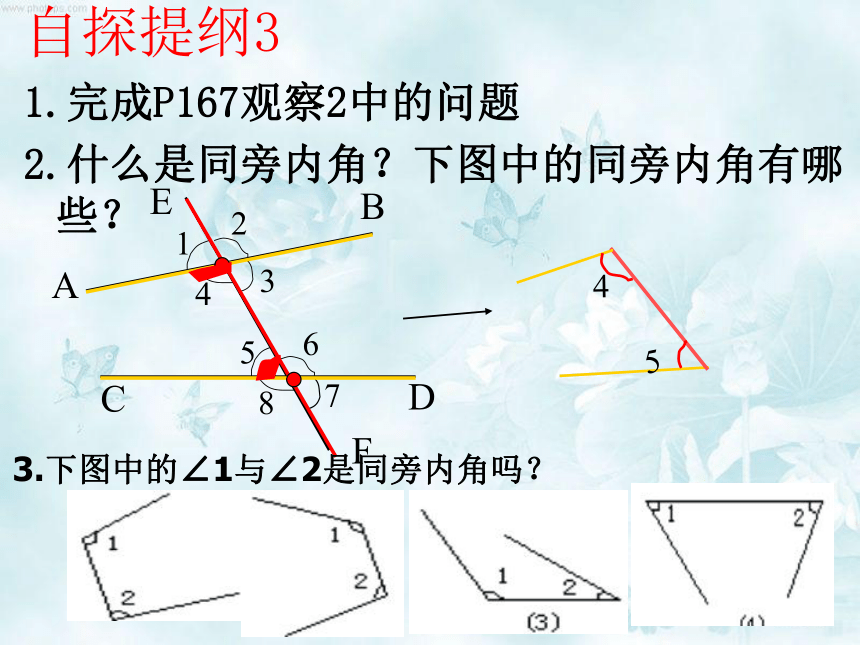
2.什么是同旁内角?下图中的同旁内角有哪些?
A
C
B
D
E
2
1
4
3
6
5
8
7
4
5
F
3.下图中的∠1与∠2是同旁内角吗?
截线
被截线
结构特征
同位角
内错角
同旁内角
内部
内部
同方
同旁
两侧
同侧
F
Z
U
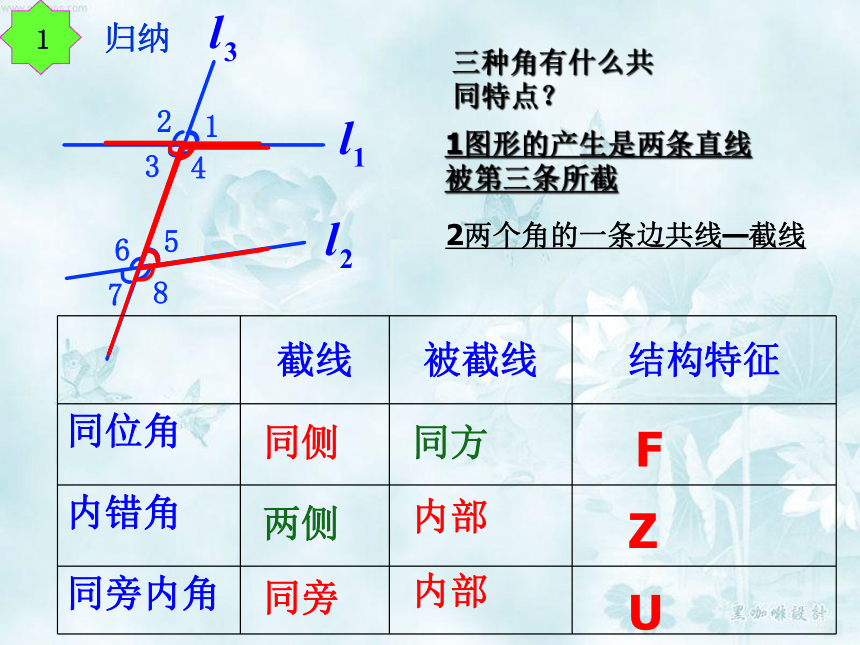
归纳
1
三种角有什么共同特点?
1图形的产生是两条直线被第三条所截
2两个角的一条边共线—截线
例:如图直线DE、BC被直线AB所截,
(1)∠1和∠2、∠1和∠3、∠1和∠4
各是什么角?
(2)如果∠1=∠4,哪么∠1和∠2相等
吗?∠1和∠3互补吗?为什么?
D
E
C
B
A
2
4
3
1
1.完成P168练习1.2
2.下列各图中 与 哪些是同位角?哪些不是?
1
2
( )
1
2
( )
( )
1
2
( )
1
2
大显身手
1.识别哪些角是同位角、内错角、 同旁内角。
1
2
(1)
同位角
1
2
(2)
1
2
(3)
1
2
(4)
1
2
(5)
a
b
c
1
2
(6)
1
2
(7)
1
2
(8)
1
2
1
2
(9)
(10)
同位角
同位角
同位角
同位角
内错角
同旁内角
(1)若ED,BF被AB所截,则∠1与_____是同位角。
∠2
2、看图填空
(2)若ED,BC被AF所截,则∠3与_____是内错角。
∠4
大显身手
(3)∠1与∠3是AB和AF
被____所截构成的_____角。
DE
内错
AB
AF
同位
(4)∠2与∠4是___和___
被BC所截构成的___ _角。
大显身手
1
2
E
D
A
C
B
1.
2.找出图中与∠1构成同旁内角的角?
1.找出图中与∠1构成内错角的角?
A
B
C
D
E
F
找出图中所有的
同位角、内错角、
同旁内角.
截线
被截线
结构特征
同位角
内错角
同旁内角
内部
内部
同方
同旁
两侧
同侧
F
Z
U
同位角、内错角、同旁内角的特点:
小结
知识的升华
独立
作业
驶向胜利的彼岸
P168
2.3
三角形个数=多边形边数-1
如果从多边形边上一点,连接多边形的各个顶点分割三角形,n边形可分割成多少个三角形?
如果沿着在三角形内部找一点,连接多边形的各个顶点,那么n边形可以分割成多少个三角形?
三角形个数=多边形边数
有两个多项式:
A=2a2 -4a+1, B=2(a2 -2a)+3,当a取任意有理数时,请比较A与B的大小.
解: ∵A-B = (2a2-4a+1 )- [2(a2-2a)+3]
= (2a2 -4a+1 )- (2a2 -4a+3)
= 2a2 -4a+1 - 2a2 +4a-3
= (2a2 - 2a2 )-(4a+4a )+(1-3)
= -2<0
∴ A -B < 0 ∴ A < B
D
E
F
1
3
4
2
两条直线CD和EF相交,构成几个角?他们之间是什么位置关系的角?
A
C
B
D
E
F
若再添加一条直线,怎样描述这三条直线的位置关系?构成几个角?
两条直线AB、CD被
第三条直线EF所截
7
1
2
3
4
5
6
8
截线
被截直线
学习目标
1.理解同位角、内错角、同旁内角的概念。
2.能从图形中找出同位角、内错角、同旁
内角。
设疑自探
同学们,根据本节课题结合学习目标,你有那些问题,请提出来。
1.理解同位角、内错角、同旁内角的概念。
2.能从图形中找出同位角、内错角、同旁
内角。
自探提纲1
1.完成P166观察中的问题
2.什么是同位角?下图中的同位角有哪些?
a
b
l
2
1
4
3
6
5
8
7
1
5
3.下图中的∠1与∠2是同位角吗?
自探提纲2
1.完成P167观察1中的问题
2.什么是内错角?下图中的内错角有哪些?
A
C
B
D
E
2
1
4
3
6
5
8
7
3
5
F
3.下图中的∠1与∠2是内错角吗?
自探提纲3
1.完成P167观察2中的问题
2.什么是同旁内角?下图中的同旁内角有哪些?
A
C
B
D
E
2
1
4
3
6
5
8
7
4
5
F
3.下图中的∠1与∠2是同旁内角吗?
截线
被截线
结构特征
同位角
内错角
同旁内角
内部
内部
同方
同旁
两侧
同侧
F
Z
U
归纳
1
三种角有什么共同特点?
1图形的产生是两条直线被第三条所截
2两个角的一条边共线—截线
例:如图直线DE、BC被直线AB所截,
(1)∠1和∠2、∠1和∠3、∠1和∠4
各是什么角?
(2)如果∠1=∠4,哪么∠1和∠2相等
吗?∠1和∠3互补吗?为什么?
D
E
C
B
A
2
4
3
1
1.完成P168练习1.2
2.下列各图中 与 哪些是同位角?哪些不是?
1
2
( )
1
2
( )
( )
1
2
( )
1
2
大显身手
1.识别哪些角是同位角、内错角、 同旁内角。
1
2
(1)
同位角
1
2
(2)
1
2
(3)
1
2
(4)
1
2
(5)
a
b
c
1
2
(6)
1
2
(7)
1
2
(8)
1
2
1
2
(9)
(10)
同位角
同位角
同位角
同位角
内错角
同旁内角
(1)若ED,BF被AB所截,则∠1与_____是同位角。
∠2
2、看图填空
(2)若ED,BC被AF所截,则∠3与_____是内错角。
∠4
大显身手
(3)∠1与∠3是AB和AF
被____所截构成的_____角。
DE
内错
AB
AF
同位
(4)∠2与∠4是___和___
被BC所截构成的___ _角。
大显身手
1
2
E
D
A
C
B
1.
2.找出图中与∠1构成同旁内角的角?
1.找出图中与∠1构成内错角的角?
A
B
C
D
E
F
找出图中所有的
同位角、内错角、
同旁内角.
截线
被截线
结构特征
同位角
内错角
同旁内角
内部
内部
同方
同旁
两侧
同侧
F
Z
U
同位角、内错角、同旁内角的特点:
小结
知识的升华
独立
作业
驶向胜利的彼岸
P168
2.3
三角形个数=多边形边数-1
如果从多边形边上一点,连接多边形的各个顶点分割三角形,n边形可分割成多少个三角形?
如果沿着在三角形内部找一点,连接多边形的各个顶点,那么n边形可以分割成多少个三角形?
三角形个数=多边形边数
有两个多项式:
A=2a2 -4a+1, B=2(a2 -2a)+3,当a取任意有理数时,请比较A与B的大小.
解: ∵A-B = (2a2-4a+1 )- [2(a2-2a)+3]
= (2a2 -4a+1 )- (2a2 -4a+3)
= 2a2 -4a+1 - 2a2 +4a-3
= (2a2 - 2a2 )-(4a+4a )+(1-3)
= -2<0
∴ A -B < 0 ∴ A < B
同课章节目录
- 第1章 走进数学世界
- 数学伴我们成长
- 人类离不开数学
- 人人都能学会数学
- 第2章 有理数
- 2.1 有理数
- 2.2 数轴
- 2.3 相反数
- 2.4 绝对值
- 2.5 有理数的大小比较
- 2.6 有理数的加法
- 2.7 有理数的减法
- 2.8 有理数加减混合运算
- 2.9 有理数的乘法
- 2.10 有理数的除法
- 2.11 有理数的乘方
- 2.12 科学记数法
- 2.13 有理数的混合运算
- 2.14 近似数
- 2.15 用计算器进行计算
- 第3章 整式的加减
- 3.1 列代数式
- 3.2 代数式的值
- 3.3 整式
- 3.4 整式的加减
- 第4章 图形的初步认识
- 4.1 生活中的立体图形
- 4.2 立体图形的视图
- 4.3 立体图形的表面展开图
- 4.4 平面图形
- 4.5 最基本的图形——点和线
- 4.6 角
- 第5章 相交线与平行线
- 5.1 相交线
- 5.2 平行线
