人教版(2012)初中数学八年级上册15.2.2分式的加减课件(15张)
文档属性
| 名称 | 人教版(2012)初中数学八年级上册15.2.2分式的加减课件(15张) |

|
|
| 格式 | ppt | ||
| 文件大小 | 1.4MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-12-25 23:29:13 | ||
图片预览





文档简介
分式的加减课件2
同分母的分式相加减,
分母不变,分子相加减.
【同分母分式加减法的法则】
回顾与思考
(2)计算:
(1)计算:
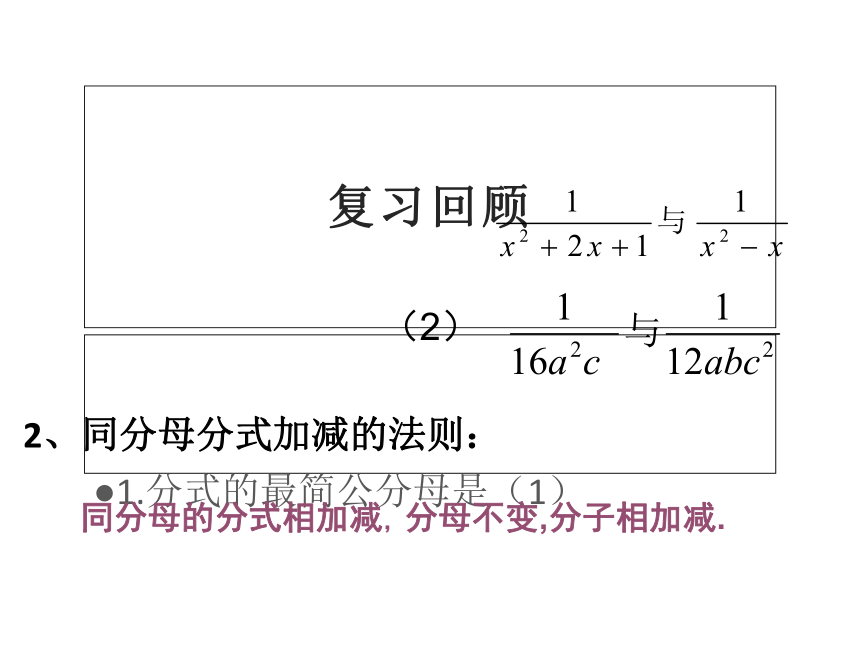
复习回顾
1.分式的最简公分母是(1)
(2)
2、同分母分式加减的法则:
同分母的分式相加减,分母不变,分子相加减.
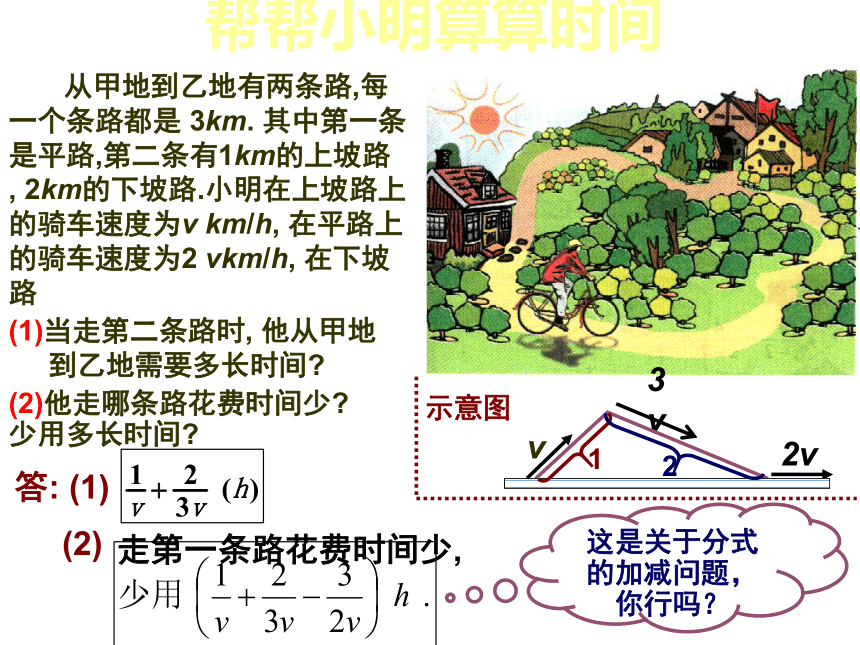
帮帮小明算算时间
这是关于分式的加减问题,你行吗?
(2)他走哪条路花费时间少?
少用多长时间?
从甲地到乙地有两条路,每
一个条路都是 3km. 其中第一条
是平路,第二条有1km的上坡路
, 2km的下坡路.小明在上坡路上
的骑车速度为v km/h, 在平路上
的骑车速度为2 vkm/h, 在下坡路
上的骑车速度为3vkm/h, 那么:
(1)当走第二条路时, 他从甲地
到乙地需要多长时间?
走第一条路花费时间少,
3v
2v
答: (1)
(2)
示意图
1
v
2
(1)异分母的分数如何加减?
(2)你认为异分母分式的加减应该如何进行?
比如 : 如何计算?
(通分,将异分母的分数化为同分母的分数)
分式的加减法(二)
2、试解决上一张的问题
解 : (1)
(2)
例 2 计算:
解:原式=
先找出最简公分母,再正确通分,转化为同分母的分式相加减。
例题解析 怎样进行分式的加减运算?
计算:
例3
解:
例题解析 吃透例题 , 成功一半
例4
计算:
分子相减时,
“减式”要配括号!
x -3
x -3
例4
计算:
解: (2)
a2 -4 能分解 :
a2 -4 =(a+2)(a-2),
其中 (a-2)恰好为第二分式的分母.
所以 (a+2)(a-2)
即为最简公分母.
分析
先找
最简公分母.
(2)
练3
:阅读下面题目的计算过程。
①
= ②
= ③
(1)上述计算过程,从哪一步开始错误,请写上该步的代号
(2)错误原因
(3)本题的正确结论为
1计算 :
又一个挑战
1
1
)
2
(
2
2
2
3
+
-
-
-
-
x
x
x
x
x
x
小结:
(1)分式加减运算的方法思路:
通分
转化为
异分母相加减
同分母
相加减
分子(整式)相加减
分母不变
转化为
(2)分子相加减时,如果分子是一个多项式,要将分子看成一个整体,先用括号括起来,再运算,可减少出现符号错误。
(3)分式加减运算的结果要约分,化为最 简分式(或整式)。
本节课你的收获是什么?
延伸与拓展
链接一:甲、乙两地相距s千米,汽车从甲地到乙地按v千米/时的速度行驶,若按(v+a)千米/时的速度行驶,可提前多少小时到达?
链接二:若 则 的值等于( )
同分母的分式相加减,
分母不变,分子相加减.
【同分母分式加减法的法则】
回顾与思考
(2)计算:
(1)计算:
复习回顾
1.分式的最简公分母是(1)
(2)
2、同分母分式加减的法则:
同分母的分式相加减,分母不变,分子相加减.
帮帮小明算算时间
这是关于分式的加减问题,你行吗?
(2)他走哪条路花费时间少?
少用多长时间?
从甲地到乙地有两条路,每
一个条路都是 3km. 其中第一条
是平路,第二条有1km的上坡路
, 2km的下坡路.小明在上坡路上
的骑车速度为v km/h, 在平路上
的骑车速度为2 vkm/h, 在下坡路
上的骑车速度为3vkm/h, 那么:
(1)当走第二条路时, 他从甲地
到乙地需要多长时间?
走第一条路花费时间少,
3v
2v
答: (1)
(2)
示意图
1
v
2
(1)异分母的分数如何加减?
(2)你认为异分母分式的加减应该如何进行?
比如 : 如何计算?
(通分,将异分母的分数化为同分母的分数)
分式的加减法(二)
2、试解决上一张的问题
解 : (1)
(2)
例 2 计算:
解:原式=
先找出最简公分母,再正确通分,转化为同分母的分式相加减。
例题解析 怎样进行分式的加减运算?
计算:
例3
解:
例题解析 吃透例题 , 成功一半
例4
计算:
分子相减时,
“减式”要配括号!
x -3
x -3
例4
计算:
解: (2)
a2 -4 能分解 :
a2 -4 =(a+2)(a-2),
其中 (a-2)恰好为第二分式的分母.
所以 (a+2)(a-2)
即为最简公分母.
分析
先找
最简公分母.
(2)
练3
:阅读下面题目的计算过程。
①
= ②
= ③
(1)上述计算过程,从哪一步开始错误,请写上该步的代号
(2)错误原因
(3)本题的正确结论为
1计算 :
又一个挑战
1
1
)
2
(
2
2
2
3
+
-
-
-
-
x
x
x
x
x
x
小结:
(1)分式加减运算的方法思路:
通分
转化为
异分母相加减
同分母
相加减
分子(整式)相加减
分母不变
转化为
(2)分子相加减时,如果分子是一个多项式,要将分子看成一个整体,先用括号括起来,再运算,可减少出现符号错误。
(3)分式加减运算的结果要约分,化为最 简分式(或整式)。
本节课你的收获是什么?
延伸与拓展
链接一:甲、乙两地相距s千米,汽车从甲地到乙地按v千米/时的速度行驶,若按(v+a)千米/时的速度行驶,可提前多少小时到达?
链接二:若 则 的值等于( )
