人教版八年级数学下册课件:18.2.2 第1课时 菱形的性质(24张)
文档属性
| 名称 | 人教版八年级数学下册课件:18.2.2 第1课时 菱形的性质(24张) |  | |
| 格式 | pptx | ||
| 文件大小 | 1.8MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-12-25 23:30:03 | ||
图片预览




文档简介
第十八章 平行四边形
18.2.2 第1课时 菱形的性质
知识回顾
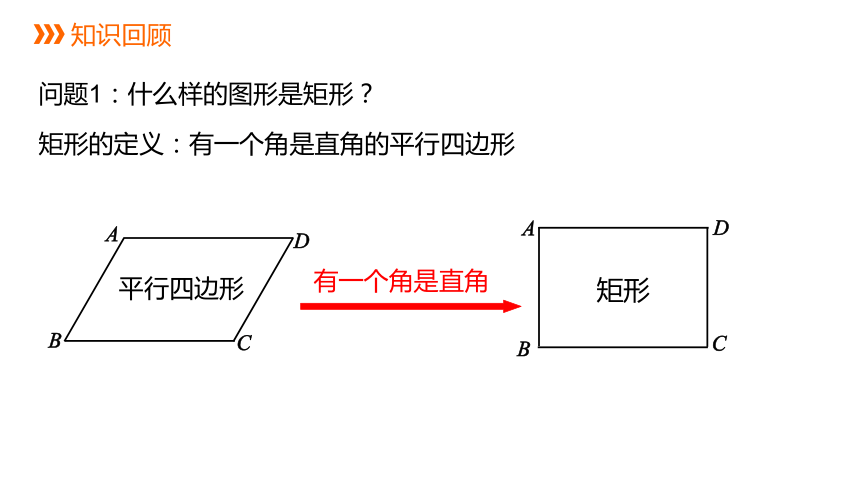
矩形的定义:有一个角是直角的平行四边形
问题1:什么样的图形是矩形?
有一个角是直角
平行四边形
矩形
问题2:平行四边形有哪些性质呢?
平行四边形的两组对边分别相等
平行四边形的两组对边分别平行
平行四边形的两条对角线互相平分
边
对角线
角
平行四边形的两组对角分别相等
平行四边形的邻角分别互补
情景导入
欣赏下面图片,图片中框出的图形是你熟悉的吗?
铁丝网
衣帽架
带图案的衣服
中国结
获取新知
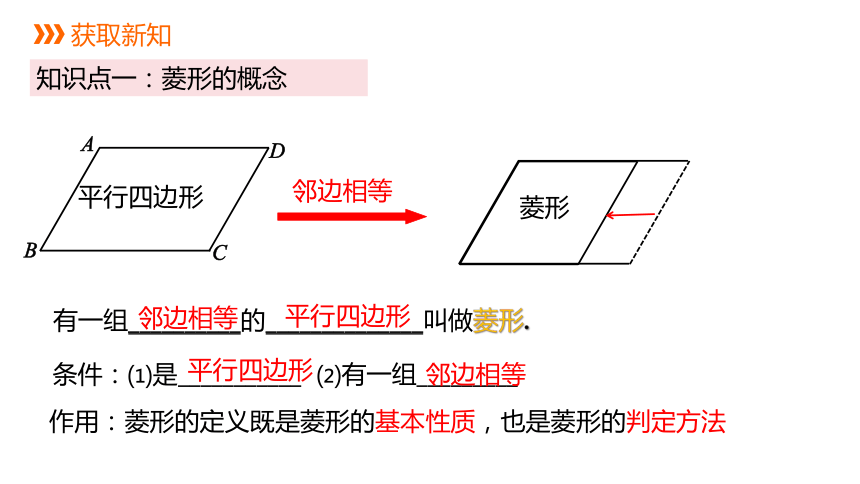
知识点一:菱形的概念
邻边相等
平行四边形
菱形
有一组__________的______________叫做菱形.
邻边相等
平行四边形
条件:⑴是___________ ⑵有一组_________
平行四边形
邻边相等
作用:菱形的定义既是菱形的基本性质,也是菱形的判定方法
例题讲解
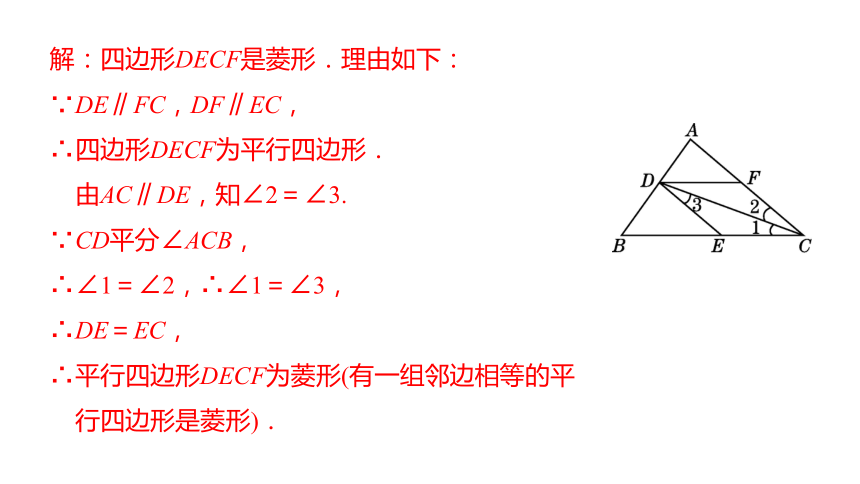
例1 已知:如图,在△ABC中,CD平分∠ACB交AB于点D,DE∥AC交BC于点E,DF∥BC交AC于点F. 四边形DECF是菱形吗?为什么?
解:四边形DECF是菱形.理由如下:
∵DE∥FC,DF∥EC,
∴四边形DECF为平行四边形.
由AC∥DE,知∠2=∠3.
∵CD平分∠ACB,
∴∠1=∠2,∴∠1=∠3,
∴DE=EC,
∴平行四边形DECF为菱形(有一组邻边相等的平
行四边形是菱形).
获取新知
知识点二:菱形的性质
问题1 菱形与平行四边形是什么关系呢?
菱形是特殊的平行四边形.平行四边形不一定是菱形。菱形具有平行四边形的所有性质
问题2 菱形是轴对称图形吗?如果是,指出它的对称轴.
问题3 猜想菱形的四边在数量上有什么关系?
菱形的两条对角线有什么关系?
是,两条对角线所在直线都是它的对称轴.
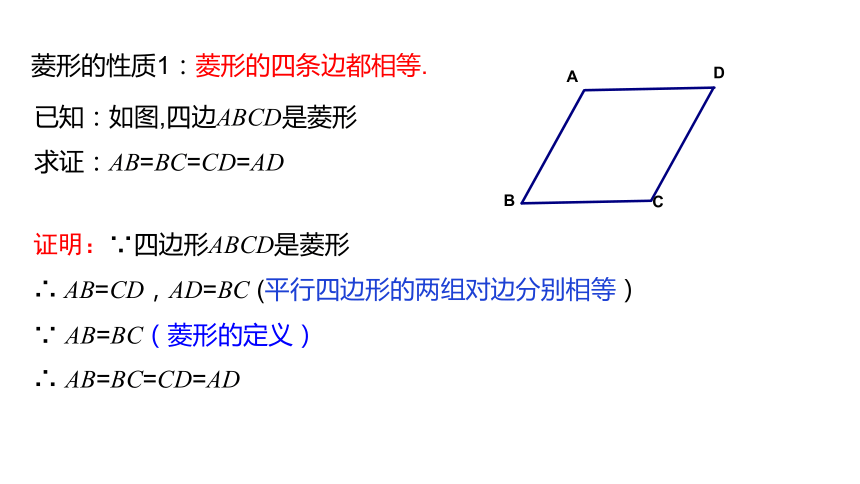
菱形的性质1:菱形的四条边都相等.
已知:如图,四边ABCD是菱形
求证:AB=BC=CD=AD
A
B
C
D
证明:∵四边形ABCD是菱形
∴ AB=CD,AD=BC (平行四边形的两组对边分别相等)
∵ AB=BC(菱形的定义)
∴ AB=BC=CD=AD
菱形的性质2:菱形的两条对角线互相垂直,
并且每一条对角线平分一组对角.
已知:如图,四边形ABCD是菱形.
证明:AC⊥BD,
AC平分∠DAB和∠DCB,BD平分∠ADC和∠ABC.
A
B
C
D
O
证明:∵四边形ABCD是菱形,
∴AD=AB(菱形的定义),
OD=OB (平行四边形的对角线互相平分),
∴ AC ⊥ DB ,AC平分∠DAB(三线合一).
同理: AC平分∠DCB ;DB平分∠ADC和∠ABC.
A
B
C
D
O
归纳总结
一:菱形的四条边都相等
几何语言:
∵四边形ABCD是平行四边形
∴AB=BC=CD=AD
二:菱形的对角线互相垂直,且平分一组对角
几何语言:
∵四边形ABCD是平行四边形
∴AC⊥BD,∠DAC=∠BAC,∠DCA和∠BCA
∠ADB=∠CDB,∠ABD和∠CBD
A
B
C
D
O
┐
例题讲解
例2 如图,在菱形ABCD中,对角线AC、BD相交于点O,BD=12cm,AC=6cm,求菱形的周长.
解:∵四边形ABCD是菱形,
∴AC⊥BD,
AO= AC,BO= BD.
∵AC=6cm,BD=12cm,
∴AO=3cm,BO=6cm.
在Rt△ABO中,由勾股定理得
∴菱形的周长=4AB=4×3 =12 (cm).
例3 如图,菱形花坛ABCD的边长为20 m,∠ABC=60°,沿着菱形的对角线修建了两条小路AC和BD. 求两条小路的长(结果保留小数点后两位)和花坛的面积(结果保留小数点后一位).
解:∵花坛ABCD的形状是菱形,
∴AC⊥BD,∠ABO = ∠ABC = × 60°= 30°.
在Rt△OAB中,AO = AB = ×20=10,
∴花坛的两条小路长AC = 2AO =20 (m),
BD = 2BO=20 ≈34. 64 (m).
花坛的面积S四边形ABCD=4×S△OAB
= AC·BD=200 ≈346. 4 (m2).
菱形的对角线将菱形分成四个全等的直角三角形,平行四边形只被对角线分成两队全等的三角形。
我们通常将菱形问题中求相关线段的长转化为求直角三角形中相关线段的长,再利用勾股定理来计算.
菱形的面积有三种计算方法:
(1)将其看成平行四边形,用底与高的积来求;
(2)对角线分得的四个全等直角三角形面积之和;
(3)两条对角线乘积的一半.
随堂演练
1.菱形具有而一般平行四边形不具有的性质是( )
A.对角相等 B.对边相等
C.对角线互相垂直 D.对角线相等
C
2.如图,在菱形ABCD中,E,F分别是AB,AC的中点,如果EF=2,那么线段CD的长是( )
A.4 B.8 C.12 D.16
A
3.如图,在菱形ABCD中,AC=8,BD=6,则△ABD的周长等于( )
A.18 B.16 C.15 D.14
B
4.如图,在菱形OABC中,点B在x轴上,点A的坐标为(2,3),则点C的坐标为 .
(2,3)
5. 如图,在菱形ABCD中,对角线AC,BD相交于点O,若∠BCO=55°,则∠CBO= °.
35
6. 如图,在△ABC中,AB=AC,四边形ADEF是菱形. 求证:BE=CE.
证明:∵四边形ADEF是菱形, ∴DE=FE,AB//FE,DE//AC, ∴∠B=∠CEF,∠C=∠BED. ∵AB=AC, ∴∠B=∠C, ∴∠BED=∠CEF. 在△DBE和△FCE中, ∵∠B=∠C,∠BED=∠CEF,DE=FE, ∴△DBE≌△FCE,
∴BE=CE.
7.如图,在菱形ABCD中,点O为对角线AC与BD的交点,且在△AOB中,OA=5,OB=12.求菱形ABCD两对边的距离h.
解:在Rt△AOB中,OA=5,OB=12,
∴S△AOB= OA·OB= ×5×12=30,
∴S菱形ABCD=4S△AOB=4×30=120.
∵
又∵菱形两组对边的距离相等,
∴S菱形ABCD=AB·h=13h,
∴13h=120,得h= .
课堂小结
菱形的性质
菱形的性质
有关计算
边
1.周长=边长的四倍
2.面积=底×高=两条对角线乘积的一半
角
对角线
1.两组对边平行且相等;
2.四条边相等
两组对角分别相等,邻角互补
1.两条对角线互相垂直平分;
2.每一条对角线平分一组对角
18.2.2 第1课时 菱形的性质
知识回顾
矩形的定义:有一个角是直角的平行四边形
问题1:什么样的图形是矩形?
有一个角是直角
平行四边形
矩形
问题2:平行四边形有哪些性质呢?
平行四边形的两组对边分别相等
平行四边形的两组对边分别平行
平行四边形的两条对角线互相平分
边
对角线
角
平行四边形的两组对角分别相等
平行四边形的邻角分别互补
情景导入
欣赏下面图片,图片中框出的图形是你熟悉的吗?
铁丝网
衣帽架
带图案的衣服
中国结
获取新知
知识点一:菱形的概念
邻边相等
平行四边形
菱形
有一组__________的______________叫做菱形.
邻边相等
平行四边形
条件:⑴是___________ ⑵有一组_________
平行四边形
邻边相等
作用:菱形的定义既是菱形的基本性质,也是菱形的判定方法
例题讲解
例1 已知:如图,在△ABC中,CD平分∠ACB交AB于点D,DE∥AC交BC于点E,DF∥BC交AC于点F. 四边形DECF是菱形吗?为什么?
解:四边形DECF是菱形.理由如下:
∵DE∥FC,DF∥EC,
∴四边形DECF为平行四边形.
由AC∥DE,知∠2=∠3.
∵CD平分∠ACB,
∴∠1=∠2,∴∠1=∠3,
∴DE=EC,
∴平行四边形DECF为菱形(有一组邻边相等的平
行四边形是菱形).
获取新知
知识点二:菱形的性质
问题1 菱形与平行四边形是什么关系呢?
菱形是特殊的平行四边形.平行四边形不一定是菱形。菱形具有平行四边形的所有性质
问题2 菱形是轴对称图形吗?如果是,指出它的对称轴.
问题3 猜想菱形的四边在数量上有什么关系?
菱形的两条对角线有什么关系?
是,两条对角线所在直线都是它的对称轴.
菱形的性质1:菱形的四条边都相等.
已知:如图,四边ABCD是菱形
求证:AB=BC=CD=AD
A
B
C
D
证明:∵四边形ABCD是菱形
∴ AB=CD,AD=BC (平行四边形的两组对边分别相等)
∵ AB=BC(菱形的定义)
∴ AB=BC=CD=AD
菱形的性质2:菱形的两条对角线互相垂直,
并且每一条对角线平分一组对角.
已知:如图,四边形ABCD是菱形.
证明:AC⊥BD,
AC平分∠DAB和∠DCB,BD平分∠ADC和∠ABC.
A
B
C
D
O
证明:∵四边形ABCD是菱形,
∴AD=AB(菱形的定义),
OD=OB (平行四边形的对角线互相平分),
∴ AC ⊥ DB ,AC平分∠DAB(三线合一).
同理: AC平分∠DCB ;DB平分∠ADC和∠ABC.
A
B
C
D
O
归纳总结
一:菱形的四条边都相等
几何语言:
∵四边形ABCD是平行四边形
∴AB=BC=CD=AD
二:菱形的对角线互相垂直,且平分一组对角
几何语言:
∵四边形ABCD是平行四边形
∴AC⊥BD,∠DAC=∠BAC,∠DCA和∠BCA
∠ADB=∠CDB,∠ABD和∠CBD
A
B
C
D
O
┐
例题讲解
例2 如图,在菱形ABCD中,对角线AC、BD相交于点O,BD=12cm,AC=6cm,求菱形的周长.
解:∵四边形ABCD是菱形,
∴AC⊥BD,
AO= AC,BO= BD.
∵AC=6cm,BD=12cm,
∴AO=3cm,BO=6cm.
在Rt△ABO中,由勾股定理得
∴菱形的周长=4AB=4×3 =12 (cm).
例3 如图,菱形花坛ABCD的边长为20 m,∠ABC=60°,沿着菱形的对角线修建了两条小路AC和BD. 求两条小路的长(结果保留小数点后两位)和花坛的面积(结果保留小数点后一位).
解:∵花坛ABCD的形状是菱形,
∴AC⊥BD,∠ABO = ∠ABC = × 60°= 30°.
在Rt△OAB中,AO = AB = ×20=10,
∴花坛的两条小路长AC = 2AO =20 (m),
BD = 2BO=20 ≈34. 64 (m).
花坛的面积S四边形ABCD=4×S△OAB
= AC·BD=200 ≈346. 4 (m2).
菱形的对角线将菱形分成四个全等的直角三角形,平行四边形只被对角线分成两队全等的三角形。
我们通常将菱形问题中求相关线段的长转化为求直角三角形中相关线段的长,再利用勾股定理来计算.
菱形的面积有三种计算方法:
(1)将其看成平行四边形,用底与高的积来求;
(2)对角线分得的四个全等直角三角形面积之和;
(3)两条对角线乘积的一半.
随堂演练
1.菱形具有而一般平行四边形不具有的性质是( )
A.对角相等 B.对边相等
C.对角线互相垂直 D.对角线相等
C
2.如图,在菱形ABCD中,E,F分别是AB,AC的中点,如果EF=2,那么线段CD的长是( )
A.4 B.8 C.12 D.16
A
3.如图,在菱形ABCD中,AC=8,BD=6,则△ABD的周长等于( )
A.18 B.16 C.15 D.14
B
4.如图,在菱形OABC中,点B在x轴上,点A的坐标为(2,3),则点C的坐标为 .
(2,3)
5. 如图,在菱形ABCD中,对角线AC,BD相交于点O,若∠BCO=55°,则∠CBO= °.
35
6. 如图,在△ABC中,AB=AC,四边形ADEF是菱形. 求证:BE=CE.
证明:∵四边形ADEF是菱形, ∴DE=FE,AB//FE,DE//AC, ∴∠B=∠CEF,∠C=∠BED. ∵AB=AC, ∴∠B=∠C, ∴∠BED=∠CEF. 在△DBE和△FCE中, ∵∠B=∠C,∠BED=∠CEF,DE=FE, ∴△DBE≌△FCE,
∴BE=CE.
7.如图,在菱形ABCD中,点O为对角线AC与BD的交点,且在△AOB中,OA=5,OB=12.求菱形ABCD两对边的距离h.
解:在Rt△AOB中,OA=5,OB=12,
∴S△AOB= OA·OB= ×5×12=30,
∴S菱形ABCD=4S△AOB=4×30=120.
∵
又∵菱形两组对边的距离相等,
∴S菱形ABCD=AB·h=13h,
∴13h=120,得h= .
课堂小结
菱形的性质
菱形的性质
有关计算
边
1.周长=边长的四倍
2.面积=底×高=两条对角线乘积的一半
角
对角线
1.两组对边平行且相等;
2.四条边相等
两组对角分别相等,邻角互补
1.两条对角线互相垂直平分;
2.每一条对角线平分一组对角
